基于VMD-PWVD的内燃机振动信号时频分析方法

岳应娟，孙 钢，蔡艳平，王 旭

（火箭军工程大学理学院，陕西西安，710025）

基于VMD-PWVD的内燃机振动信号时频分析方法

岳应娟，孙 钢，蔡艳平，王 旭

（火箭军工程大学理学院，陕西西安，710025）

针对Wigner-Ville分布（WVD）在分析多分量信号时交叉干扰项与时频聚集性相互矛盾的问题，提出一种基于变分模态分解的伪魏格纳分布法（VMD-PWVD），以抑制WVD分布中的交叉项。该方法首先对信号进行VMD分解，将信号在频域上进行剖分，得到一组相互独立的具有不同频率的固有模态函数（IMF）分量，然后对每个IMF分量进行PWVD分析，最后把各个IMF分量的PWVD分析结果线性叠加，重构原始信号的时频分布。仿真结果表明，该方法在有效地从频域和时域双向抑制WVD交叉项的同时，又保留了WVD分布法原有的优良特性。将VMD-PWVD应用于内燃机缸盖振动信号的时频分析中，能很好地刻画出不同工况信号的特征信息，各时频分量物理意义明确，是一种有效的时频分析方法。

内燃机；振动信号；时频分析；WVD；VMD-PWVD；交叉项；变分模态分解

内燃机缸盖振动信号往往包含着丰富的故障信息。由于振动分析诊断方法具有不解体性和实时性，目前仍一直是内燃机状态监测和故障诊断的研究热点。如何从简单的一维振动信号中提取出故障信息，是故障诊断最关键也最困难的环节，直接关系到故障诊断的准确性和故障早期预报的可靠性［1］。

内燃机振动信号具有较强的非线性、非平稳时变特征，传统的分析方法并不适用。目前非平稳信号处理的主要手段有基于短时傅里叶变换、S变换、Wigner-Ville分布（WVD）、小波变换和希尔伯特-黄变换的时频分析，其中WVD分布对振动信号的边缘特性、瞬时频率和局域化等都有很好的描述，但由于交叉干扰项的影响，很难将包含多个频率成分的信号表示清楚，限制了其应用。为减小交叉干扰项对WVD分布的影响，赵培洪等［2］通过设计二维遮蔽滤波器将交叉项移除；程发斌等［3］将ASTFT谱作为窗函数对信号的WVD进行加窗处理，从而有效消除掉WVD中的交叉项；刘文艺等［4］从研究WVD自项和交叉项的相互关系入手，提出了一种利用SPWVD谱抑制WVD交叉项的方法。本文则在前人研究的基础上，将变分模态分解（variational mode decomposition，VMD）与PWVD时频分析相结合，以期解决WVD聚集性与交叉项成分抑制相互制约的问题，并将该方法应用于内燃机缸盖振动信号的分析处理中，以验证其有效性。

1　VMD-PWVD时频分析法

1.1变分模态分解（VMD）算法

VMD是一种全新的自适应信号处理方法，它通过迭代搜寻变分模型的最优解来确定每个本征模态函数（IMF）分量的频率中心及其带宽，实现了信号频域和各个分量的自适应剖分，它是一种完全非递归的信号分解方法。

信号经过VMD被分解成一系列IMF分量，每个IMF分量都可以表示为一个调幅-调频信号，用uk（t）表示，其表达式为［5］

式中:Ak（t）为uk（t）的瞬时幅值，且Ak（t）≥0；k（t）为uk（t）的相位。

uk（t）的瞬时频率ωk（t）=（t），ωk（t）≥0。 Ak（t）和ωk（t）相对于k（t）来说变化是缓慢的。在［t-δ，t+δ］（δ≈2π/（t））的时间范围内，uk（t）可以看作幅值为Ak（t）、频率为ωk（t）的谐波信号。

IMF的带宽可通过以下3个步骤进行估算:①对每一个模态信号uk（t），通过Hilbert变换计算与之相关的解析信号；②对每一个模态信号uk（t），通过加入指数项调整各自估计的中心频率，把模态信号的频谱变换到基带上；③对解调信号进行H1高斯平滑估计。

假设信号经VMD分解得到K个IMF分量，则变分约束模型为

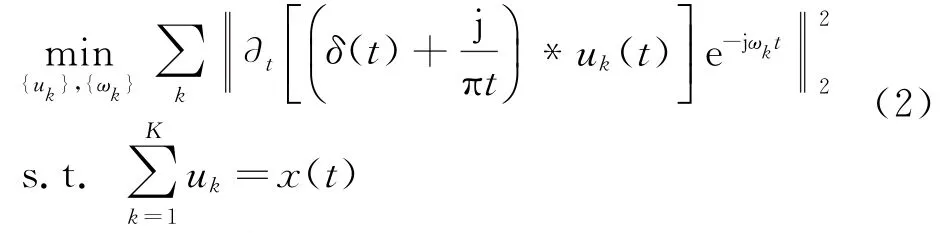
式中:δ（t）为Dirac函数；*表示卷积；uk（k=1，2，…，K）代表信号经VMD分解后得到的K个IMF分量；ωk为各个IMF分量的频率中心；j为虚数单位；t为时间；x（t）为原始信号。

为求取变分约束模型的最优解，引入二次罚函数项和拉格朗日乘子便可得到:

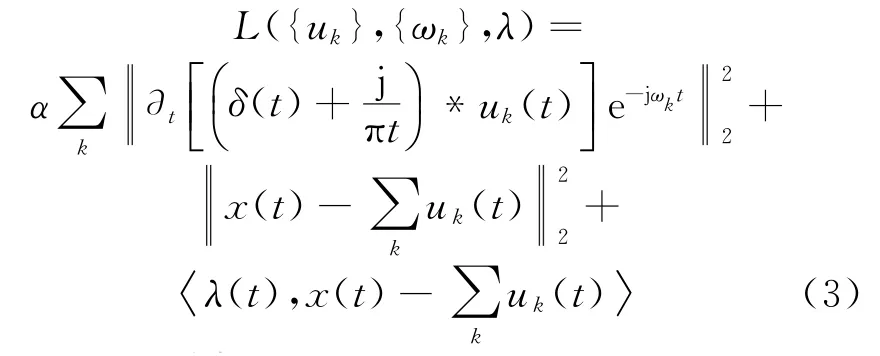
式中:α为惩罚参数；λ为拉格朗日乘子。

VMD算法中采用乘法算子交替的方法来求取上述变分约束模型，得到最优解，将信号分解成为K个窄带IMF分量［6］，其实现流程如下:

（2）n=n+1，执行整个循环；

（3）k=0，k=k+1，当k＜K时，首先执行内层第一个循环，根据下式更新uk:

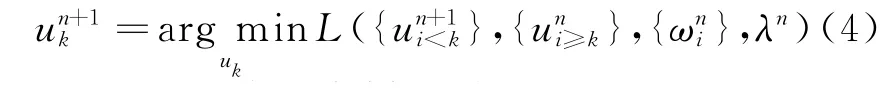
然后执行内层第二个循环，根据下式更新ωk:

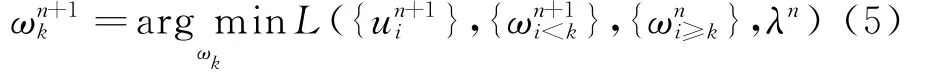
（4）根据下式更新λ:

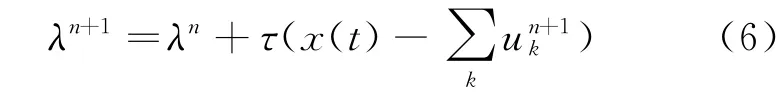
式中:τ表示更新参数。

1.2伪魏格纳分布（PWVD）算法

针对信号x（t），WVD的理论定义如下［7］:

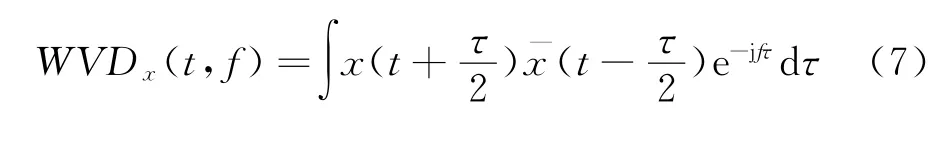
式中:f表示信号的瞬时频率。

WVD是二次时频分布，由于双线性核函数的引入，使得多个信号分量在时频平面内产生耦合作用，产生了交叉项。当信号中包含的分量成分越多，交叉项也越多，若信号含有n个分量，则会产生n（n-1）/2个交叉项。交叉干扰项的存在导致了虚假信号和假频问题的产生，使WVD时频分析很难将有多个频率成分的信号表示清楚［］。

Cohen类双线性变换方法中的PWVD可以抑制WVD中交叉项的干扰。对WVD进行加窗处理后得到PWVD，其定义如下:

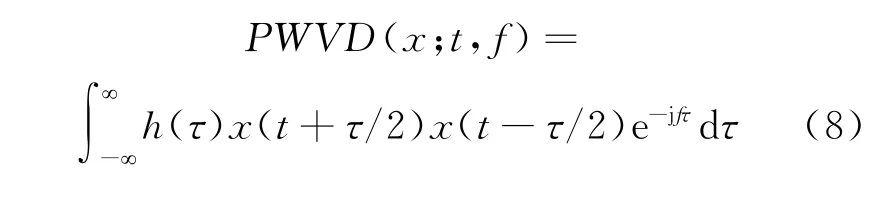
式中:h（τ）为窗函数。

1.3VMD-PWVD时频分析

WVD出现频率混叠和干扰现象的主要原因是被分析的信号序列不是单分量的，而是由多个单分量的信号叠加而成。本文利用线性时频分布满足叠加原理的思想，提出了VMD-PWVD时频分析法。为消除交叉干扰项，可以将待分析的信号经VMD进行频域剖分，分解成一组单分量信号，先对各个单分量信号单独进行PWVD分析和处理，在时域上通过窗函数消除干扰项，再将结果线性叠加，这样在时域和频域都会对交叉干扰项起到很好的抑制作用。使VMD-PWVD时频分析法既能有效消除WVD的交叉干扰项，又可保留原WVD法的优良特性。

信号x（t）的VMD-PWVD时频分布定义为:

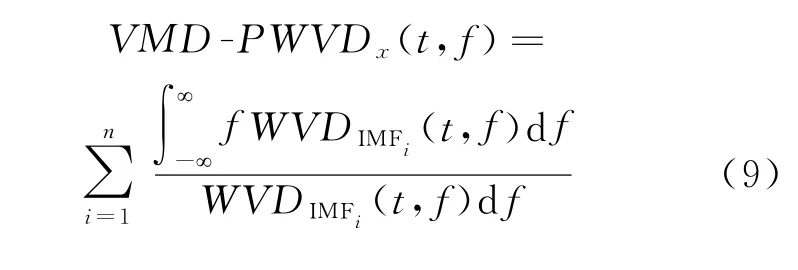
2　仿真及实测验证

2.1仿真计算

取多分量信号x（t）为仿真信号。设高斯计算中x（t）由4个原子复合而成，其位置分别为（t1，Ω1）=（28，0.1）、（t2，Ω2）=（28，0.4）、（t3，Ω3）=（100，0.1）和（t4，Ω4）=（100，0.4）。仿真信号的时域波形图和时频相平面图如图1所示。

图2给出了仿真信号的WVD时频分布图。由图2中可以看出，x（t）的WVD分布有4个自项，其时频位置分别为（28，0.1）、（28，0.4）、（100，0.1）和（100，0.4），有5个交叉项，分别位于各自项连线的中心位置，其中心分别在（28，0.25）、（64，0.4）、（64，0.25）、（64，0.1）、（100，0.25）处，其中（64，0.25）处的交叉项是2个交叉项的叠加。

对WVD时频分布作加窗处理得到x（t）的PWVD时频图，如图3所示。从图3可看出，这时位于（64，0.4）、（64，0.25）、（64，0.1）的交叉项得到控制，但位于（28，0.25）、（100，0.25）的交叉项仍然存在。这是因为PWVD分析的窗函数在时域上会对交叉干扰项起到抑制作用，但对频域上的交叉干扰项并没有进行处理。

图1　仿真信号的时域波形图和时频相平面图Fig.1 Time-domain waveform and time-frequency phase plane image of simulation signal

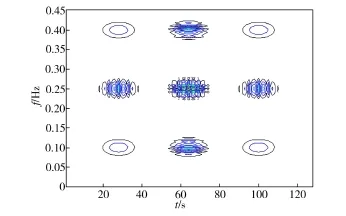
图2　WVD时频分布图Fig.2 WVD time-frequency distribution

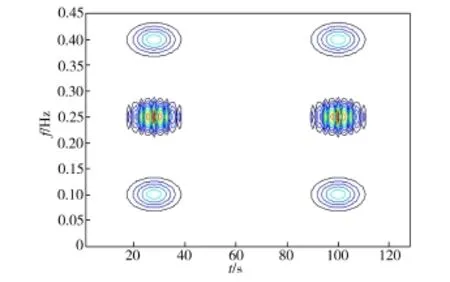
图3　PWVD时频分布图Fig.3 PWVD time-frequency distribution

对x（t）使用本文提出的VMD-PWVD时频分析方法进行分析处理，得到的时频分布图如图4所示。由图4中可见，经VMD-PWVD分析后，所有的交叉项被去除，使自项在时频域内可分辨得很清楚。

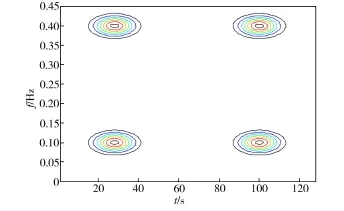
图4　VMD-PWVD时频分布图Fig.4 VMD-PWVD time-frequency distribution

2.2实测验证

试验所用内燃机为6135型柴油机。试验平台由柴油机、传动轴、电机和控制台4部分组成。试验中，第2缸气阀上的进气门间隙固定为0.3 mm，排气门设置4种工况，分别为排气阀气门间隙正常（0.3 mm）、过小（0.06 mm）、过大（0.5 mm）工况以及排气阀严重漏气工况，其中排气阀严重漏气工况通过在排气阀上开4 mm×1 mm的方口来模拟。取内燃机第2缸盖表面振动信号对内燃机进行故障诊断，采样频率为25 k Hz，测试过程中，内燃机空载运行，转速为1500 r/min。

首先对采集到的振动信号进行VMD分解。进行VMD分解时需预先设定分解层数K，K的值可根据分解后得到的各模态分量中心频率不同的特点，采用观察中心频率的方法确定。首先选用正常工况的信号进行分析，不同K值下信号的中心频率如表1所示。由表1可见，从K=5开始，所得到的后两阶IMF分量的中心频率值基本不再发生变化，且在分解结果中出现了中心频率相近的模态分量，表明信号出现了过分解，故取K=4为宜。采用上述方法对另外3种工况下的缸盖表面振动信号进行分解，结果表明K=4时，4种工况下的振动信号在频域分解适宜，不会出现模态混叠。为此取K=4对不同工况下的振动信号进行VMD分解，并提取相应的IMF分量。分解过程中令惩罚参数α=2000，权值参数τ=0.3，以保证实际分解信号的保真度。

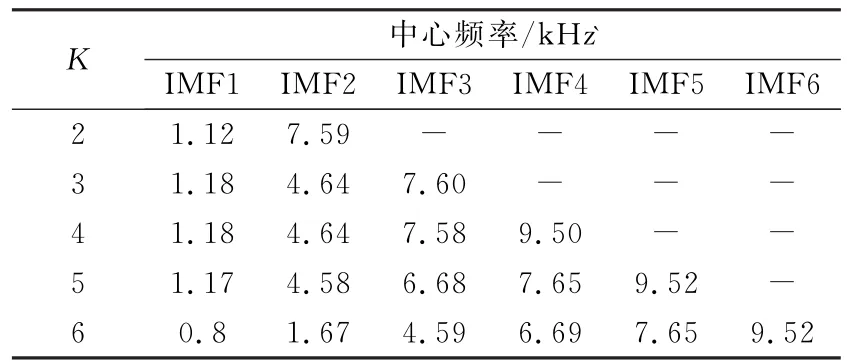
表1　不同K值下分解所得信号分量的中心频率Table 1 Center frequency of signal components under different K

接着，对VMD分解得到的一组IMF分量分别进行PWVD分析（窗参数采用Hanning窗，窗长155），再通过线性叠加得到振动信号的VMDPWVD时频分布图如图5所示，并与相同信号的WVD时频分布图（见图6）进行比较。

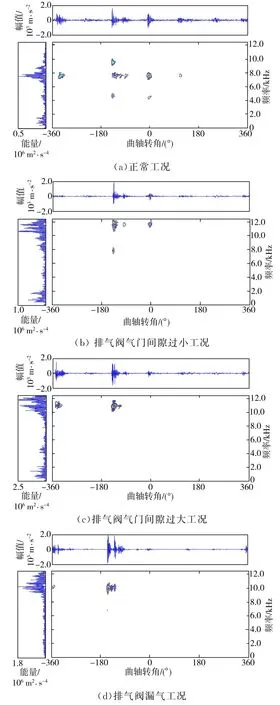
图5　振动信号的VMD-PWVD时频分布Fig.5 VMD-PWVD time-frequency distribution of vibration signals

图6　振动信号的WVD时频分布Fig.6 WVD time-frequency distribution of vibrations signals

由柴油机工作原理可知，进气门开启的角度在排气上止点前20°附近，关闭的角度在进气下止点后48°附近；排气门开启的角度在做功下止点前48°附近，关闭的角度在排气上止点后20°附近；点火时刻对应曲轴转角为0°。柴油机进排气阀开闭与曲轴转角的关系图如图7所示。柴油机缸盖表面振动信号主要由工作过程中气阀与气阀座的撞击以及排气阀开启时气流的冲击和燃烧产生的激振引起。对于多缸柴油机，邻缸的振动激励也会产生较大影响［9］。因此，根据图7可知，4种工况下振动信号的时频分布图在曲轴转角为-340°、-132°、0°、132°和340°附近应有冲击分量存在，其中-340°和-132°附近冲击分量对应的分别是排气门和进气门关闭时气阀与气阀座冲击引起的振动；0°附近冲击分量对应的是缸内混合气体爆燃、柴油机做功引起的振动；132°和340°附近冲击分量分别为排气阀和进气阀开启所引起的冲击。

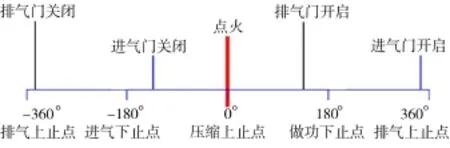
图7　内燃机燃烧和气阀开闭与曲轴转角关系图Fig.7 Relationship between the crank angle and the valve switching and combustion in the ICE

从图6中可以看出，WVD时频分布图中除上述曲轴转角附近存在有冲击分量外，在-236°、-66°、66°和236°附近不同程度存在冲击分量，这些冲击分量明显属于交叉干扰项，对后续的分析识别都有很大干扰，且图6中时频聚集性差，难以从图中看出各冲击分量包含的具体频率成分；而由图5中可以看出，VMD-PWVD时频分布图时频聚集性好，交叉项得到很好抑制，各工况下振动信号的时频谱区别明显，时频振动分量与图7所示进、排气阀开闭以及点火一一对应，在时频域内具有明确的物理意义，且不同工况下各冲击分量的时频位置明显不同，易于判断故障类型，表明VMD-PWVD时频分析法是一种有效的内燃机故障振动信号时频分析方法。

由上分析可知，内燃机缸盖振动信号是一种混有大量噪声干扰的非平稳周期信号，具有局部冲击信号的特点，是多分量混合信号，直接计算其WVD时频分布，不可避免地会在时频平面内产生耦合作用，生成很多交叉项。由于VMD分解的计算方法是在频域对信号进行剖分，信号在频域上被分解成单分量信号，即同一阶IMF信号频率相近，这样，对单分量信号进行PWVD时频分析再将结果线性叠加，就极大抑制了WVD时频分布在频域层面内的交叉干扰项。采用PWVD分析是对WVD分析作加窗处理，通过窗函数可以很好地抑制时域空间内的交叉干扰项。因此从理论上来说，即便变分模态分解出现了过分解或分解不彻底现象（即K值过大或过小），抑或窗函数参数选取不得当，使未被分解出来的频率成分仍夹杂在信号中，对其进行PWVD分析时仍会出现在WVD时间-频率空间中的相应位置，能量的分布并不会因分解层数的不同或窗函数的选取而发生错误。由此可知，基于VMD的PWVD时频分析方法能够有效抑制WVD时频分布的交叉干扰项。

3　结语

本文提出的基于VMD的PWVD时频分析方法利用了线性时频分布满足叠加原理的思想，结合了VMD频域自适应剖分频域上抑制交叉干扰项的特点和PWVD窗函数时域抑制交叉干扰项的优点，不仅可以有效地在时频域抑制交叉干扰项，而且还保留了WVD分布的所有优良特性，是一种有效的时频分析方法。将VMD-PWVD方法应用于内燃机缸盖振动信号的分析中，可以有效地对4种典型气阀机构工况特征信息进行描述，各时频分量具有严格的物理意义。

［1］蔡艳平，李艾华，王涛，等.基于时频谱图与图像分割的柴油机故障诊断［J］.内燃机学报，2011，29（2）: 181-186.

［2］赵培洪，平殿发，邓兵.抑制Wigner-Ville分布交叉项的新方法［J］.计算机应用，2010，30（8）:2218-2220.

［3］程发斌，汤宝平，刘文艺.一种抑制维格纳分布交叉项的方法及在故障诊断中应用［J］.中国机械工程，2008，19（14）:1727-1731.

［4］刘文艺，汤宝平，陈仁祥，等.一种应用自项抑制魏格纳分布交叉项的方法［J］.中国机械工程，2009，20（21）:2613-2616.

［5］Dragomiretskiy K，Zosso D.Variational mode decomposition［J］.IEEE Transactions on Signal Processing，2014，62（3）:531-544.

［6］唐贵基，王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用［J］.西安交通大学学报，2015，49（5）:73-81.

［7］刘伟.基于改进的WVD的旋转机械故障诊断研究［D］.昆明:昆明理工大学，2013.

［8］王成栋.时频图像及其在机械设备故障自动诊断中的应用［D］.西安:西安交通大学，2004.

［9］王成栋，张优云，夏勇.模糊函数图像在柴油机气阀故障诊断中的应用研究［J］.内燃机学报，2004，22（4）:162-168.

［责任编辑 郑淑芳］

Time-frequency analysis of ICE vibration based on VMD-PWVD

Yue Yingjuan，Sun Gang，Cai Yanping，Wang Xu
（College of Science，Rocket Force University of Engineering，Xi’an 710025，China）

In light of the problem of Wigner-Ville distribution（WVD）in the analysis of multi-component signals that traditional methods cannot suppress the cross-terms while holding high time-frequency resolution，a cross term suppression method named VMD-PWVD is proposed.Firstly，multi-component signals are decomposed into intrinsic mode functions（IMFs）in frequency zone by VMD. Then，the PWVD distributions of each IMF are computed.Finally，PWVDs of each single component signal are added linearly to reconstruct the WVD of the original signal.Test on synthetic data confirms that the proposed method can effectively suppress the cross-terms in both frequency and timezone while holding high time-frequency resolution.Used in the time-frequency analysis of the internal combustion engine（ICE）vibration signals，the method proves effective and can well depict the characteristic information of signals under different conditions with clear physical meanings of frequency component.It is thus concluded that VMD-PWVD is an effective method for time-frequency analysis.

ICE；vibration signal；time-frequency analysis；WVD；VMD-PWVD；cross-terms；variational mode decomposition

TK418；TN911.6

A

1674-3644（2016）05-0365-06

2016-03-23

国家自然科学基金资助项目（51405498）；陕西省自然科学基金资助项目（2013JQ8023）；中国博士后科学基金资助项目（2015 M582642）.

岳应娟（1972-），女，火箭军工程大学教授，博士.E-mail:yingjuanyue@163.com