周期为2n的二元序列谱免疫度的算法

杨 波，刘能飞，佘 冰，李寿贵

（1.武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北武汉，430065；2.武汉科技大学理学院，湖北武汉，430065）

周期为2n的二元序列谱免疫度的算法

杨 波1，刘能飞2，佘 冰2，李寿贵1

（1.武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北武汉，430065；2.武汉科技大学理学院，湖北武汉，430065）

通过对周期序列谱免疫度的研究，提出了序列的0限制k错线性复杂度的概念。以Mark Stamp所提出的计算周期为2n的二元序列k错线性复杂度的算法为基础，设计了求周期为2n的二元序列0限制k错线性复杂度的算法1，并利用算法1提出了确定该二元序列谱免疫度的快速算法，该算法具有较高的计算效率，时间复杂度为O（n）。

流密码；线性复杂度；k错线性复杂度；二元序列；谱攻击；谱免疫度；快速算法

流密码安全的一个重要指标是序列的线性复杂度。线性复杂度是指产生一个给定序列的线性反馈移位寄存器的最小级数r。利用著名的Berlekamp-Massey算法［1］，一个敌手窃取序列的2r个连续比特就可以得到该序列的联接多项式，即完全确定了产生该序列的线性反馈移位寄存器。因此，密码学中一个强的序列必须具有高的线性复杂度。

设序列的周期为l，Berlekamp-Massey算法可能需要至少输入l个连续比特才能使输出稳定于正确的联接多项式和线性复杂度，因此当线性复杂度较高且周期较长时，Berlekamp-Massey算法的计算量非常大。为了解决这一问题，Games等［2］研究发现，当序列的周期为2n时，通过n步计算就可以求出其线性复杂度和联接多项式，进而提出了Games-Chan算法。然而有些序列的线性复杂度虽然很高，但改变少量比特后其线性复杂度降为0，稳定性极差，很容易被破解，为此Stamp等［3］提出了k错线性复杂度概念。k错线性复杂度是指改变原始序列每个周期中小于等于k个相应比特所得到的序列的线性复杂度最小值。Stamp等在文献［3］中还设计了一个计算周期为2n的二元序列k错线性复杂度的高效算法。此后，国内外学者对线性复杂度和k错线性复杂度算法进行了一系列研究［4-10］，得到了一些适用于不同周期或不同有限域上的序列的线性复杂度或k错线性复杂度快速算法。

序列具有高的线性复杂度和k错线性复杂度只是流密码安全性强的必要条件。2011年Gong等［11］提出了针对流密码的快速选择性离散傅里叶谱攻击。在一般情况下，谱攻击比代数攻击更有效、更灵活［12-13］。为了使序列能够抵抗快速选择性离散傅里叶谱攻击，Gong等在文献［11］中同时给出了谱免疫度的概念，即序列或其补序列的非零零化序列的最小线性复杂度，并在文献［14］中算法1的基础上设计了一个计算周期为l（l|2n-1）的序列的谱免疫度算法。

本文通过研究谱免疫度和k错线性复杂度之间的联系，提出0限制k错线性复杂度的概念，然后在文献［3］中求周期为2n的二元序列k错线性复杂度算法的基础上，设计一个计算2n周期二元序列0限制k错线性复杂度的算法，并进一步提出一个计算该二元序列谱免疫度的算法，采用这一算法可以在2n步内得到计算结果。

1　预备知识

令s∞=（s0，s1，…，si，…）是周期为l的二元序列，向量s=（s0，s1，…，sl-1）表示s∞中的一个周期，向量s的汉明重量其中表示整数加法（下同）。设a和b均为l维向量，定义两向量的乘积a·b=c，其中ci=ai·bi、“·”为GF（2）上的乘法运算；定义两向量的和a+b=c，其中ci=ai+bi、“+”为GF（2）上的加法运算。记，其中表示周期序列s∞的线性复杂度，l维向量a和b的汉明距离记作

定义1（k错线性复杂度［15］）周期序列s∞的k错线性复杂度记作ck（s），

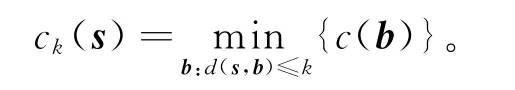
定义2（谱免疫度［11］）设s∞是一个具有周期l的二元序列，称

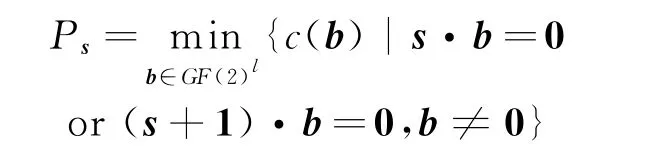
为序列s∞的谱免疫度。

定义3（0限制k错线性复杂度）周期序列s∞的0限制k错线性复杂度记作c0k（s），

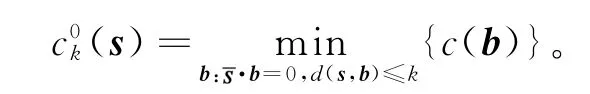
根据谱免疫度定义和上述分析即得定理1。

定理1 周期为l的二元序列s∞的谱免疫度等于的0限制错线性复杂度和s∞的0限制w（s）-1错线性复杂度的最小值，即

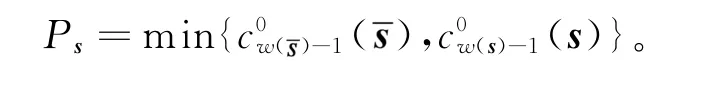
2　快速算法

首先在文献［3］中求周期为2n的二元序列k错线性复杂度算法的基础上，给出一个求周期为2n的二元序列0限制k错线性复杂度的算法，然后基于定理1，给出一个求周期为2n的二元序列谱免疫度的快速算法。

2.1算法1：0限制k错线性复杂度算法

输入:周期为2n的二元非零序列s∞中的一个周期（这里要求k≤ w（s）-1）。

输出:序列s∞的0限制k错线性复杂度c。

算法程序伪代码:

下面用一个算例来进一步说明算法1。

例1 设序列s∞的周期为64，其一个周期序列为s=100010100010000011001000000110100000 0100100111001010010000001111，利用算法1可求出序列s∞的0限制k=21错线性复杂度是28。具体计算过程如下。

初始值:l=64，k=21，a=s，c=0，m=0

第一步:l=32，k=21，t=20w（b）=16

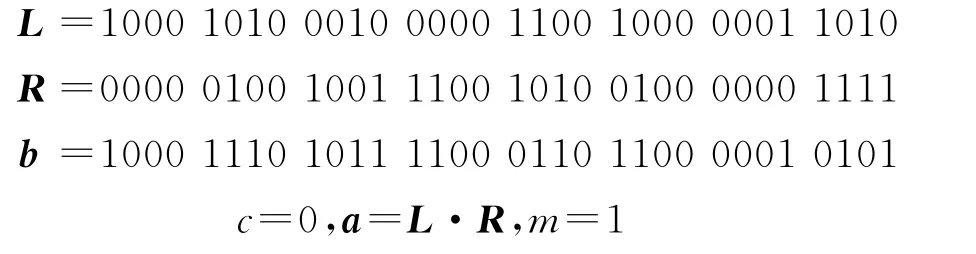
第二步:l=16，k=5，t=21w（b）=6

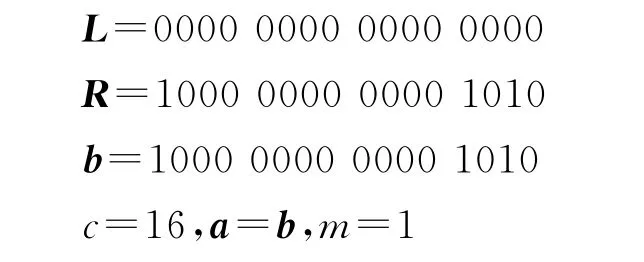
第三步:l=8，k=5，t=21w（b）=6

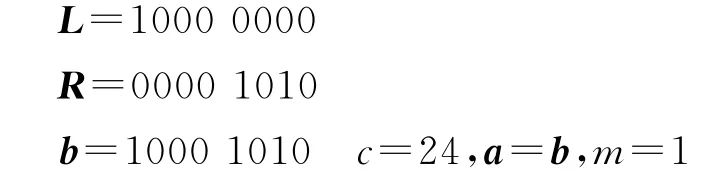
第四步:l=4，k=5，t=21w（b）=2

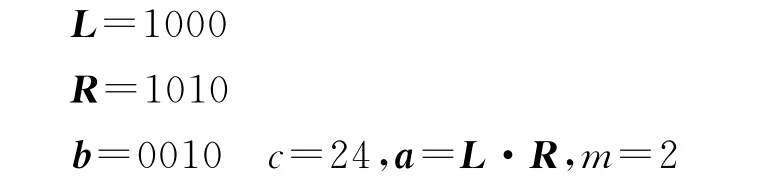
第五步:l=2，k=3，t=22w（b）=4

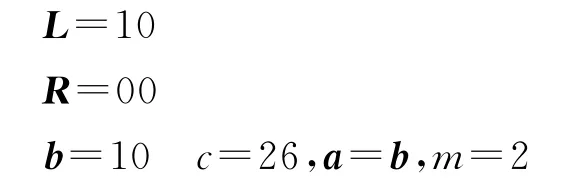
第六步:l=1，k=3，t=22w（b）=4

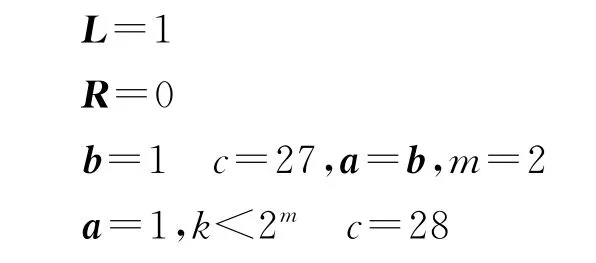
2.2算法1正确性的证明

设S2（2n）表示周期为2n的所有二元序列的集合，若s∞∈S2（2n），算法1仅需考虑s∞的一个周期s。设si表示s的第i比特；L（s）表示s的左半部分的长度为2n-1；R（s）表示s的右半部分，的长度为2n-1；符号aj（1≤j≤n）表示算法1中第j步循环所得到的向量a；a0表示初始向量s，即第一步循环前的向量a；符号bj（1≤j≤n）表示算法1中第j步循环所得到的向量b；符号表示将bj的第i比特由 1改为0时所对应的初始向量s中可能修改的比特的集合。算法1中的m表示在循环过程中向量b改为0的次数。

引理1 设s∞∈S2（2n），则

证明:利用数学归纳法证明如下。

（1）当j=1时，即算法1执行第一步循环得到b1。由可得si=1、si+2n-1=0或si=0、si+2n-1=1，若要将由1改为0，按照0限制的要求，此时需要将si或由1改为0，所以

当j=r时，即算法1执行到第r步循环得到br。若要将由1改为0，由于则有或由于0不能改变，所以此时需要将或由1改为0，这等同于修改或由的定义和归纳假设，有

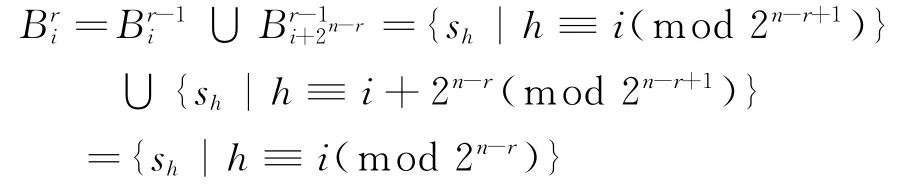
由（1）和（2），引理1得证。

引理2 如果算法1在第j步循环可以将bj改为0，那么将bj中1个值为1的比特改为0将使得初始向量s中2m个相应的值为1的比特改为0。

证明:注意到m是向量b改为0的次数，其初始值为0，m随b的这种修改而增加。对m进行数学归纳如下。

（1）当m=0时，若在第r1步循环可以将修改为0，则av=bv=L（av-1）+R（av-1），1≤v＜ r1。因此，第r1步中和中值为1的比特对应s中的1个值为1的比特。由于与文献［3］中的k错线性复杂度算法不同，由0限制的原则，将中1个值为1的比特改为0将对应修改L或中1个值为1的比特，因此使得初始向量s中2m=20=1个相应的值为1的比特修改为0。

算法1在第r1步循环将修改为0后，m=1且中每个值为1的比特对应着中各1个值为1的比特，从而对应s中2m=2个值为1的比特。

（2）假设当m=u-1时，若在第r2（＞r1）步循环可以将修改为0，那么将中1个值为1的比特改为0将使得初始向量s中2u-1=2m个相应的值为1的比特改为0。

当m=u时，若在第j（＞r2）步循环可以将bj修改为0，有av=bv=L（av-1）+R（av-1），r2＜v＜j，因此，第j步循环中L（aj-1）和R（aj-1）中值为1的比特对应s中2u个值为1的比特。由于bj=L（aj-1）+R（aj-1），由0限制的原则，将bj中1个值为1的比特改为0将对应修改L（aj-1）或R（aj-1）中1个值为1的比特，因此使得初始向量s中2u=2m个相应的值为1的比特改为0。

由（1）和（2），引理2得证。

引理3 如果在算法1的第j步循环要将bj修改为0，则要修改初始向量s中相应的w（bj）× 2m个值为1的比特。

证明:由引理2，将bj中某个值为1的比特改为0，等价于将初始向量s中2m个值为1的比特改为0；由引理1，显然i1≠i2。所以，若将bj修改为0需要修改s中 w（bj）×2m个值为1的比特。

定理2 令s∞∈S2（2n），0≤k＜w（s），算法1能在n步内求出序列s∞的0限制k错线性复杂度。

证明:当k=0时，算法1实际上就是文献［2］中的Games-Chan算法。如果k＞0，可以通过将s中不超过k个值为1的比特改为0，尽可能地将s的线性复杂度减到最小。

根据Games-Chan算法，当b≠0时，s的线性复杂度将增大，因此减小线性复杂度的方法是尽可能地将每一步的b改为0。具体的策略是:如果在第j步循环能将bj修改为0，必须将其修改为0。这是因为，如此修改将使线性复杂度减小2n-j，而即使第j步循环之后每步都能将b改为0，线性复杂度最多减小2n-j。由引理3，第j步若要将bj修改为0，将对应修改初始向量s中w（bj）×2m个值为1的比特，所以在第j步能否将bj修改为0，取决于是否w（bj）×2m≤k。若第j步将bj修改为0，初始向量s中可被修改的值为1的比特数将减小为k-w（bj）×2m。显然算法1将在循环n步后结束，且值为0的比特是不可能被修改的，所以算法1能在n步内求出序列s∞的0限制k错线性复杂度。证毕。

2.3算法2：谱免疫度算法

算法1给出了一个通用的0限制k错线性复杂度算法，也就是k的值可以取小于w（s）的任何非负整数。依据定理1，本文在算法1的基础上提出了算法2，具体如下。

输入:周期为2n的二元非零序列s∞中的一个周期

输出:序列s∞的谱免疫度P。

算法步骤:

（1）以s、序列周期l=2n、w（s）-1作为算法1的输入，输出s∞的0限制w（s）-1错线性复杂度cs。

（3）计算P=min｛cs，c｝。

由算法步骤可知，算法2可以在2n步内计算出周期为2n的二元序列的谱免疫度，即算法2的时间复杂度为O（n）。

3　结语

序列的谱免疫度是流密码安全的一个新标准。本文讨论了谱免疫度与k错线性复杂度的内在联系，提出了0限制k错线性复杂度的概念，并给出计算周期为2n的二元序列0限制k错线性复杂度的快速算法，在此基础上提出了求周期为2n的二元序列谱免疫度的算法，该算法能在2n步内得到计算结果，具有较高的计算效率。

［1］Massey J L.Shift-registers synthesis and BCH decoding［J］.IEEE Transactions on Information Theory，1969，IT-15（1）:122-127.

［2］Games R A，Chan A H.A fast algorithm for determining the complexity of a binary sequence with period 2n［J］.IEEE Transactions on Information Theory，1983，IT-29（1）:144-146.

［3］Stamp M，Martin C F.An algorithm for the k-error linear complexity of binary sequences with period 2n［J］.IEEE Transactions on Information Theory，1993，39（4）:1398-1401.

［4］Kaida T，Uehara S，Imamura K.An algorithm for the k-error linear complexity of sequences over GF（pm）with period pn，p a prime［J］.Information and Computation，1999，151:134-147.

［5］Xiao Guozhen，Wei Shimin，Lam K Y，et al.A fast algorithm for determining the linear complexity of a sequence with period pnover GF（q）［J］.IEEE Transactions on Information Theory，2000，46（6）: 2203-2206.

［6］Wei Shimin，Xiao Guozhen，Chen Zhong.A fast algorithm for determining the minimal polynomial of a sequence with period 2pnover GF（q）［J］.IEEE Transactions on Information Theory，2002，48（10）: 2754-2758.

［7］Wei Shimin，Xiao Guozhen，Chen Zhong.An efficient algorithm for k-error linear complexity［J］. Chinese Journal of Electronics，2002，11（2）:265-267.

［8］魏仕民，肖国镇，陈钟.确定周期为2npm二元序列线性复杂度的快速算法［J］.中国科学:E辑，2002，32（3）:401-408.

［9］Chen Hao.Fast algorithms for determining the linear complexity of sequences over GF（pm）with period 2tn［J］.IEEE Transactions on Information Theory，2005，51（5）:1854-1856.

［10］Meidl W.Reducing the calculation of the linear complexity of u2v-periodic binary sequences to Games-Chan algorithm［J］.Des Codes Cryptogr，2008，46（1）:57-65.

［11］Gong Guang，Rønjom S，Helleseth T，et al.Fast discrete Fourier spectra attacks on stream ciphers［J］.IEEE Transactions on Information Theory，2011，57（8）:5555-5565.

［12］Courtois N T，Meier W.Algebraic attacks onstream ciphers with linear feedback［C］//Advances in Cryptology-EUROCRYPT 2003.Springer，2003，LNCS 2656:345-359.

［13］Helleseth T，Rønjom S.Simplifying algebraic attacks with univariate analysis［C］//Information Theory and Applications Workshop，New York: IEEE，2011:1-7.

［14］Gong Guang.Sequences，DFT and resistance against fast algebraic attacks［C］//Sequences and Their Applications（SETA 2008）.Springer，2008，LNCS 5203:197-218.

［15］Niederreiter H，Shparlinski I E.Periodic sequences with maximal linear complexity and almost maximal k-error linear complexity［C］//Proceedings of Cryptography and Coding，9th IMA International Conference.Springer，2003，LNCS 2898:183-189.

［责任编辑 尚 晶］

Algorithm for spectral immunity of binary sequences with period 2n

Yang Bo1，Liu Nengfei2，She Bing2，Li Shougui1
（1.Hubei Province Key Laboratory of Systems Science in Metallurgical Process，Wuhan University of Science and Technology，Wuhan 430065，China；2.College of Science，Wuhan University of Science and Technology，Wuhan 430065，China）

The concept of 0-constrained k-error linear complexity of a sequence is firstly presented by means of studying the spectral immunity of a periodic sequence.Then an algorithm（A1）for computing the 0-constrained k-error linear complexity of a given binary sequence with period 2nis designed based on the algorithm for computing the k-error linear complexity of this kind of sequences proposed by Mark Stamp.Finally，on the basis of algorithm A1，a fast algorithm for determining the spectral immunity of binary sequences with period 2nis proposed.This algorithm is efficient and its time complexity is O（n）.

stream cipher；linear complexity；k-error linear complexity；binary sequence；spectral attack；spectral immunity；fast algorithm

TP309；TN918.1

A

1674-3644（2016）05-0382-05

2016-04-22

湖北省自然科学基金资助项目（2013CFA131）；武汉科技大学冶金工业过程系统科学湖北省重点实验室开放基金资助项目（Y201315）；武汉科技大学大学生科技创新基金研究项目（14ZZB100）.

杨 波（1973-），男，武汉科技大学副教授，博士.E-mail:boyangcn@126.com