基于DEM边坡强度折减分析
张 婧,赵 波
(1.重庆建工市政交通工程有限责任公司,重庆 400000;2.重庆建工集团股份有限公司设计研究院,重庆 400000)
基于DEM边坡强度折减分析
张婧1,赵波2
(1.重庆建工市政交通工程有限责任公司,重庆 400000;2.重庆建工集团股份有限公司设计研究院,重庆 400000)
基于传统的强度折减理论,探讨了离散元背景下的强度折减理论,并用FLAC软件进行验证。结果表明:采用本文的强度折减方法与传统的强度折减理论得到的边坡安全系数、边坡位移、滑体滑裂面位置和形状基本一致,表明本文的强度折减方法具有一定的合理性与科学性。
离散元(DEM);边坡;强度折减;验证分析
强度折减法作为边坡稳定性验算的一种普遍方法,由于其不需要事先假定滑裂面,可直接求出边坡的安全系数,方便快捷而被广泛使用[1-5]。郑颖人院士首先把强度折减的思路引入国内,并提出等效六面体的强度折减[6-9]。奕茂田等对强度折减收敛准则进行研究。郑宏、刘金龙等在此基础上进行了进一步的细化分析研究[10-12]。以上研究均基于连续介质(如有限元,有限差分等)的强度折减,但土体实际上是由离散土颗粒组成的,是离散接触,采用有限元只能进行近似的研究。离散元(DEM)最一种近年来出现的较新计算理论,可以高效模拟土体的大应变、大变形,正被快速应用于边坡的稳定分析[13-15]。本文基于传统强度折减理论,对离散元中强度折减的应用进行研究分析。
1 强度折减理论
1.1传统强度折减理论
强度折减的基本思想是不断折减粘聚力和内摩擦角的值,见式(3),直到坡体失稳。边坡安全系数F就是边坡临界状态时的折减系数,其数学表达式为:
(1)
将式(1)左右两边同时除F得:
(2)
强度折减的最终折减参数表达式为:
(3)
1.2离散元强度折减方法
基于传统强度折减理论,对离散元的相关参数进行处理计算边坡的安全系数。由于离散元的参数主要表征土颗粒之间相互作用关系,属于微观参数范畴,确定微观折减参数是进行离散元强度折减的第一步。根据目前宏微观参数的对应关系和土体颗粒相关影响参数的研究结论,土体的微观参数主要为颗粒间的摩擦系数与土颗粒间的粘结参数,这两个参数与宏观参数中的内摩擦角和粘聚力相互对应[16]。其折减表达为:
(4)
2 计算模型及参数确定
2.1计算模型
如图1所示,本文强度折减的计算基本模型。此边坡的坡高20 m,边坡斜率为1:1,其离散元模型和有限元模型均基于此模型尺寸建立。
如图2所示为本文的离散元模型。该离散元模型采用落雨法生成,所谓落雨法就是先让颗粒在自己设定好的空间内进行颗粒的自由落体堆积(模型边界采用wall element进行限定),在自由堆积稳定后,根据要求删除多余的颗粒。该方法可以更加准备模拟边坡土体的初始应力,避免传统边坡建模方法造成的初始应力失真及采用半径扩大法删除上部边界墙体时,由于相互作用力过大导致颗粒“外溢”,造成模拟失真。具体模拟步骤如图2所示。
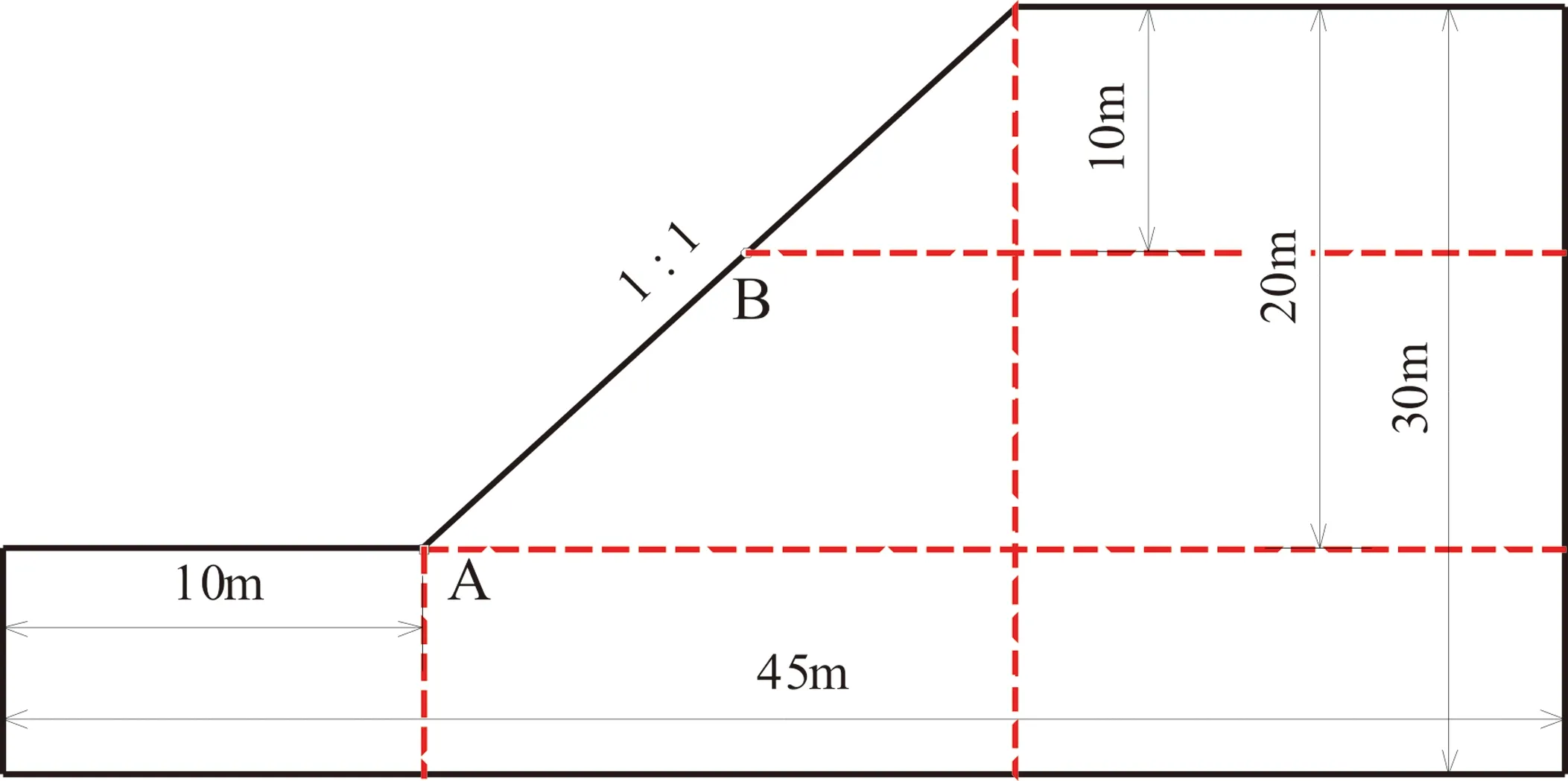
图1 计算模型
图3为边坡的有限元网格模型,有限元程序采用Itasca的有限元软件FLAC。模型的左右边界限制其法向位移,底面边界限制所有方向位移。
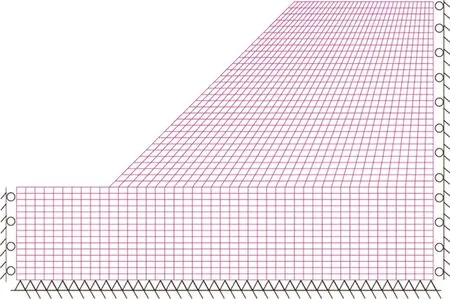
图3 有限元网格模型
2.2宏细观参数标定
宏观参数和细观参数的确定采用参数标定法。参数标定采用一系列的细观双轴试验去校核试验室得到的土体宏观参数。本文主要涉及黏土,故土颗粒采用平行粘结接触。双轴试验采用的模型尺寸为10 m×20 m,颗粒半径为0.2 m~0.3 m,采用均匀分布,共生成3 406个颗粒,见图4。
双轴标定试验分别在围压1 MPa、1.5 MPa和2 MPa三种情况下进行,如图5所示。土体的弹性模量和泊松比可以通过线弹性条件下的加载和卸荷试验获取,土体的内摩擦角和粘聚力则通过莫尔圆来获取,见图6,内摩擦角的数学表达式为[17]:
(5)
式中:σ1、σ3分别为最大主应力、最小主应力。表1、表2分别为土体的宏观、微观参数表。
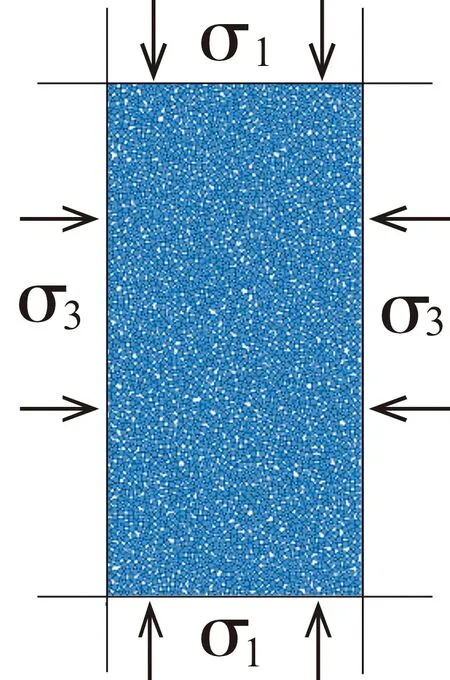
图4 双轴模型
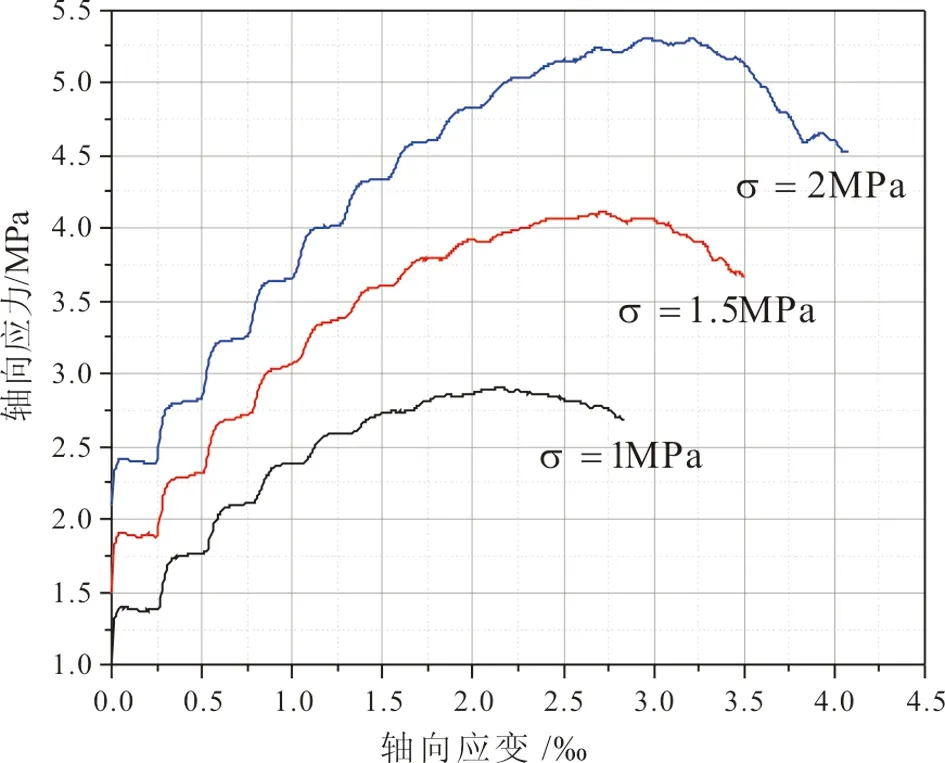
图5 不同围压下应力-应变曲线图
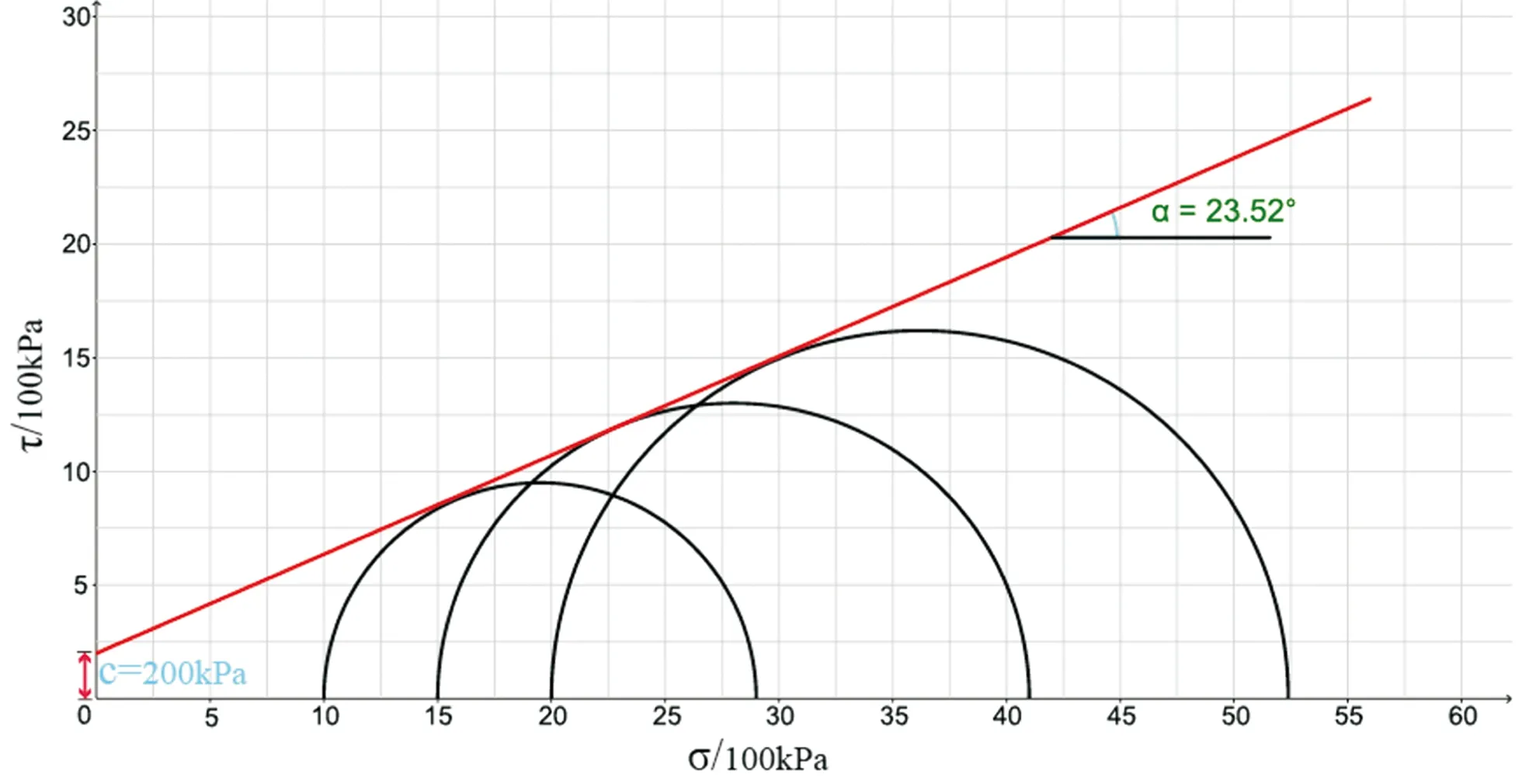
图6 莫尔圆图

弹性模量E/MPa泊松比v粘聚力c/kPa内摩擦角φ/(°)密度/(kg·m-3)580.2420023.522300

表2 土体微观参数表
3 结果分析
采用有限差分软件FLAC进行强度折减具有较为成熟的计算理论,一般采用计算收敛、塑性区贯通和坡脚位移突变进行边坡是否失稳的判据。参考借鉴有关有限差分的边坡失稳判据和进行基于DEM(离散元)的边坡稳定性的一些基本特征,文中在进行基于DEM的强度折减时,其失稳判据:(1) 当坡体有显著变位时,以坡体的累积位移或位移突变作为边坡失稳判据;(2) 当坡体无明显变位时,以土颗粒的不平衡力<0.1 N,且最大不平衡力与平均不平衡力的比值小于10作为计算结束的标准。从1开始每次折减0.1,待确定大致范围后(如1.1~1.2),每次折减0.01直至求出安全系数。
经过计算基于DEM的PFC的边坡安全系数为1.24,基于有限元的FLAC计算出的安全系数为1.19,相对误差为4%,在可控范围内。
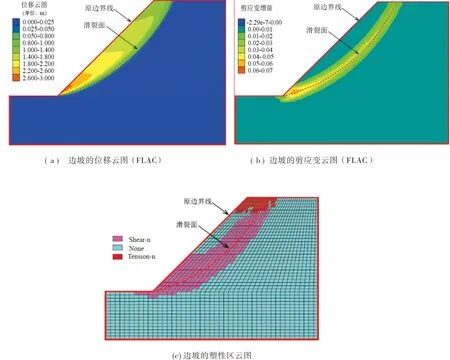
图7 FLAC计算出的边坡相关图
图7为采用FLAC在安全系数0.81情况下边坡的相关图(位移云图、剪应变云图、塑性区云图)。通过有限差分比较成熟的强度折减理论计算出的边坡应有的位移、滑裂面和剪应变等信息,为采用PFC进行边坡的强度折减得出的相关信息进行验证分析。
如图8所示为基于离散元(PFC)边坡的相关图(位移图、土颗粒运动方向图、土颗粒转动图)。由图8(a)可知,边坡的滑体呈现外部位移较大,内部位移较小,且滑体与稳定区有明显的分界面-滑裂面,且滑裂面呈现弧形。由图8(b)可知,在滑裂面附近土颗粒的运动方向与滑裂面近乎平行,整个滑体区域运动方向呈现沿着滑裂面向下滑动。由图8(c)可知,在滑体的中上部区域土颗粒旋转较大,主要还是分布在滑裂面(红虚线)以上的滑体中。
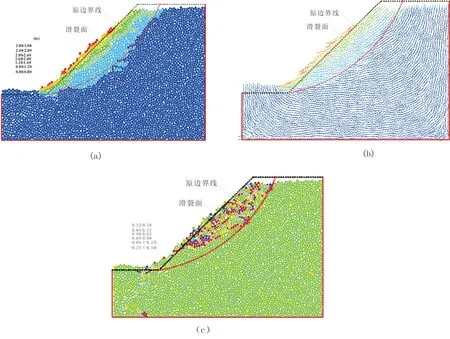
图8 PFC计算出的边坡的相关图
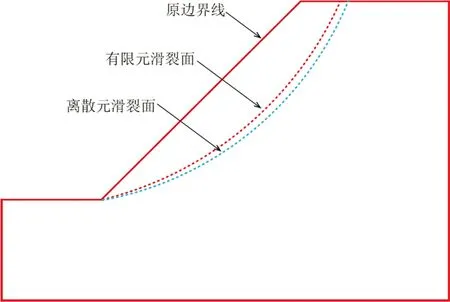
图9 不同计算理论下边坡滑裂面
结合图7、图8,采用有限元和离散元计算得出的边坡的最大位移几乎相等,土体的不同部位处的位移也相差不大。同时两者的坡体滑裂面均呈现弧形,且其弧形相差不大,这说明采用DEM进行边坡稳定性计算与安全系数计算是相对可靠的。采用DEM进行边坡的安全系数计算时,可以直观的观测到土体的变形,具有较优的可视性。
如图9所示,为不同计算理论下(离散元、有限差分)边坡滑裂面分布图。从图9可知,离散元与有限差分的滑裂面均呈现弧形,且均从坡脚处开始,两个滑裂面相差不大,可近似认为滑裂面相同。
通过对FLAC计算的边坡安全系数进行对比,采用基于DEM进行的强度折减理论所得到的安全系数、边坡位移和滑裂面的位置与形状和采用FLAC进行强度折减得到的边坡的安全系数、边坡位移、滑裂面的位置与形状基本一致,说明采用本文基于DEM的强度折减方法具有一定的可行性与科学性。
[1]MATSUI T,SAN K C.Finite element slope stability analysis by shear strength reduction technique[J].Soils and Foundations,1992,32(1):59-70.
[2]AWSON E M,ROTH W H,DRESCHER A.Slope stability analysis by strength reduction[J].Geotechnique,1999,49(6):835-840.
[3]ZHENG H,LIU D F,LI C G.On the assessment of failure in slope stability analysis by the finite element method[J].Rock Mechanics and Rock Engineering,2008,41:629.
[4]Duncan J M.State of the art:limit equilibrium and finite-element analysis of slopes.Journal of Geotechnical engineering,1996,122(7):577-5960
[5]Griffiths D V, Lane P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3) :387—403.
[6]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57- 61.
[7]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.
[8]赵尚毅,郑颖人,张玉芳.极限分析有限元讲座—Ⅱ有限元强度折减折减法中边坡失稳的判据探讨[J],岩土力学,2005,26(2):332-336.
[9]赵尚毅,郑颖人,时卫民等.用有限单元强度折减法求边坡稳定安全系数[J],岩土工程学报,2002,34(3):343-346.
[10]栾茂田,武亚军,年延凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.
[11]刘金龙,栾茂田,赵少飞等.关于强度折减有限元方法中边坡失稳判据的讨论[J],岩土力学,2005,26(8):1345-1348.
[12]郑宏,李春光,李焯芬,等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):626-628.
[13]曾远.土体破坏细观机理及颗粒流模拟[D].上海:同济大学,2006.
[14]张晓平,吴顺川,张志增等.含软弱夹层土样变形破坏过程细观数值模拟及分析[J].岩土力学,2008,29(5):1200-1204.
[15]吴顺川,张晓平,刘洋.基于颗粒元模拟的含软弱夹层类土质边坡变形破坏过程分析[J].岩土力学,2008,29(11 ):2900-2904.
[16]周健,王家全,曾远等.颗粒流强度折减法和重力增加法的边坡安全系数研究[J].岩土力学,2009,30(6):1549-1555.
[17]Han-Jiang L,Jun-Jie Z,Jun Zhang.DEM analysis of soil-arching within geogrid-reinforced and unreinforced pile-supported embankments[J].Computers and Geotechnics.2014(61),13-23.
Slope strength reduction investigation based on DEM
ZHANG Jing1,ZHAO Bo2
(1.ChongqingConstructionEngineeringMunicipalTrafficEngineeringCo.Ltd.,Chongqing400000,China;2.DesignandResearchInstituteofChongqingConstructionEngineeringGroupGroupCo.,Ltd.Chongqing400000,China)
Based on the strength reduction theory,the strength reduction theory of the discrete element is discussed,and the FLAC software is used to verify the theory.The results show that the strength of this reduction by using the strength reduction method and traditional reduction theory obtains the safety coefficient of slope,slope displacement,landslide sliding position and shape of the basic agreement,which shows that the strength reduction method has certain rationality and scientific nature.
DEM;slope;strength reduction;verification analysis
2016-03-30
国家自然科学基金(51408086);重庆市研究生科研创新项目(CYS14165)
张婧(1989—),女,河南许昌人,助理工程师。
1674-7046(2016)05-0016-07
10.14140/j.cnki.hncjxb.2016.05.004
TU470
A

