一种电路机理等效的船舶 Nomoto 模型
张显库,杨光平
(大连海事大学 航海学院,辽宁 大连 116026)
一种电路机理等效的船舶 Nomoto 模型
张显库,杨光平
(大连海事大学 航海学院,辽宁 大连 116026)
为使船舶 Nomoto 模型方程形象化,用电阻、电容和放大器搭建电路,经推导其传递函数与船舶Nomoto 模型相同,通过适当选取电路元件参数,实现“育鲲轮”的电路机理等效模型。将融入旋回降速补偿后的电路仿真实验结果与实船回转试验结果进行比对,证明电路机理模型可以较高精度等效船舶 Nomoto 模型,对船舶运动半物理仿真具有重要指导意义。
船舶模型;电路;等效
0 引 言
建立数学模型是分析系统性能、控制器设计及系统仿真的关键。船舶运动数学模型一般可由理论推导、系统辨识、实船试验等方法获得[1-6]。船舶运动数学模型是否有较高的精度一切以是否与实船试验结果符合较好为标准,实船试验费用太昂贵,数字仿真试验不直观。本文希望以 Matlab 电路系统工具箱中的电路元件搭建一个系统,来实现软件半物理仿真,其数学方程与推导的船舶运动数学方程相同。文献[1]介绍了一种电路网络的快速建模方法,本文将其反过来使用,即将数学模型变成电路网络,使之等效于船舶Nomoto 模型。Nomoto 模型虽然是一种最简单的船舶运动数学模型,但因其参数只有 2个且物理意义明显,故在船舶操纵性能预报和线性控制器设计等方面仍然具有较好的应用价值。相对地,以日本学派为代表的船舶运动分离型数学模型和以欧美学派为代表的整体型船舶运动数学模型因参数众多,且大部分参数求取使用回归公式或经验公式,对于新型船舶或大型船舶,其模型的精度并不能保证。故本文研究使 Nomoto 模型形象化仍然具有较好的实用价值。
1 等效电路
式(1)给出了从舵角输入 δ 到船首向输出 ψ 的传递函数形式 Nomoto 数学模型 G(s),式中 K和T 在航海领域中分别称为旋回性指数和追随性指数。
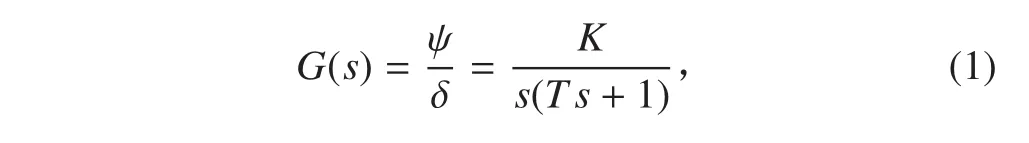
观察式(1)可知它由比例、积分和一阶惯性 3个环节组成。比例和积分环节的实现需要放大器元件,而一阶惯性环节可由一阶 RC 网络实现。将文献[1]中使用电路网络法获得传递函数数学模型理解透彻后,可反过来使用该方法,将传递函数的数学模型变成电路网络,图1给出了式(1)最后的实现电路。
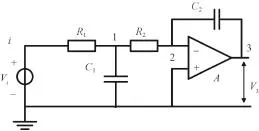
图1 Nomoto 模型等效电路Fig. 1 An equivalent Nomoto model by circuit
由文献[1]给出的快速推导传递函数数学模型方法,该电路由 3个有效节点组成,有 1个放大器元件,分母中除了含放大器元件回路项外,其他项都可省略,得到数学模型的过程如下:
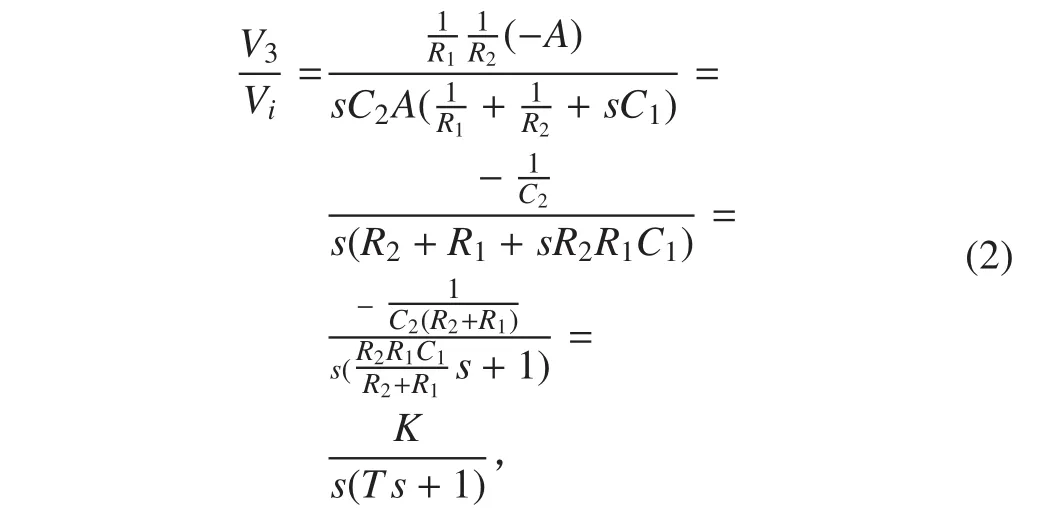
为了简化,令 R1=R2,则
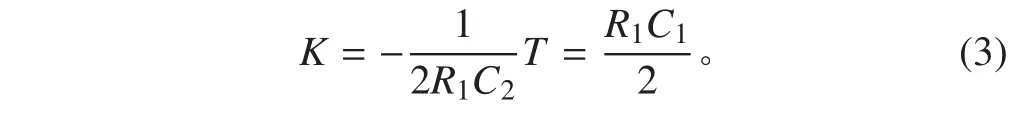
以大连海事大学教学科研实习船“育鲲”为例,其船舶两柱间长为105 m,船宽 18 m,吃水 5.4 m,排水体积 5 735.5 m3,实验航速 15 kn(设计航速 16.7 kn),方形系数为0.559 5,舵叶面积 11.46 m2,理论计算 K=-0.28 s-1,T=71.84 s。船舶实际回转时都有速度下降,30°舵角回转实验时船舶转一圈速度可降为初始速度的48%,而使用电路网络实现的船舶模型难以实现回转时的速度下降,但可进行相应的影响折算[7-10]。海上试验时速度下降、水深变浅等影响折合成对 K,T 的改变,都是减小 K、增大 T,使船舶的旋回和操纵性能下降。进行 30°舵角海上旋回试验时,其影响最终折合为K=-0.167 s-1,T=115.8 s,则由式(3)可设:R1=R2=1 200 Ω,C1=0.193 F,C2=0.0025 F。
2 仿真实验
使用 Matlab 2010b 的 Powerlib 电路系统工具箱进行仿真。在 Powerlib 工具箱中不存在放大器元件,如图2所示利用电阻元件、电压测量元件、Gain 增益元件、可控电压源元件和Powergui 元件构建一个放大器元件[11],全选后单击鼠标右键选择“create subsystem”进行封装,再单击右键选择“Mask subsystem”,在弹出的图3~图5窗口中按所示设置好各参数。注意图3绘制放大器元件形状的 3 根线时,使用 Plot 函数时如plot([0 0],[-1 1]),绘制直线的 2个坐标点是横坐标放在一个向量里、纵坐标放在一个向量里,即 2个坐标点实际为(0,-1)和(0,1)。另外图2中元件的变量名要与图4中的变量名设为一致。图6给出最后的使用电路元件进行 30°舵角回转的仿真实验框图,图中最右侧的 Gain 元件用于弧度变角度的转换。船舶位置是根据仿真得出的船首向角 ψ、初始航速 u=15 kn 使用计算得出。图7给出了电路仿真结果与实船试验结果的比较,图7中稍高一些的曲线为实船试验曲线,稍低一些的曲线为电路等效 Nomoto 模型仿真曲线,船舶的横纵坐标都除了船长 L。
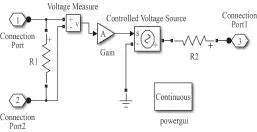
图2 放大器元件构建Fig. 2 Building amplifier
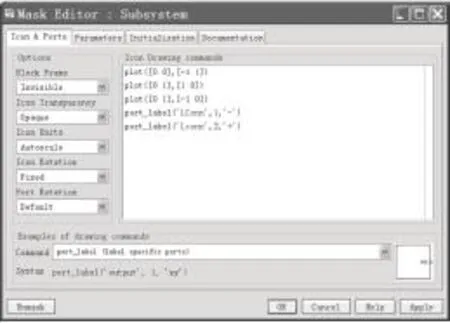
图3 放大器参数设置界面一Fig. 3 First setting window of amplifier parameters
为了方便分析,定义了式(4)所示的曲线符合度。使用曲线符合度的概念可以较好地说明仿真曲线与实船试验曲线的符合程度。
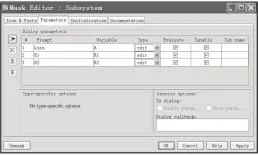
图4 放大器参数设置界面二Fig. 4 Second setting window of amplifier parameters
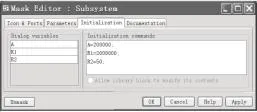
图5 放大器参数设置界面三Fig. 5 Third setting window of amplifier parameters
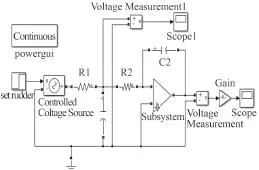
图6 仿真电路图Fig. 6 Circuit diagram of simulation
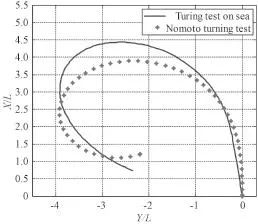
图7 仿真结果Fig. 7 Simulation result

由图7可知,仿真时横向战术直径 3.5 L,实船3.35 L;仿真时纵向战术直径 2.8 L,实船 3.6 L,横向纵向平均符合度为86.8%。因为进行了速度和水深影响的折合,其精度比 Nomoto 模型本身的精度稍高。Nomoto 模型的优点是形式简单、只有 2个参数且物理意义明显,但精度不高是其不足。如果 Nomoto 模型与实船试验的结果曲线符合度能达到 90%以上,反而难以让人相信。
3 另外一种解法
深入研究发现,Nomoto 模型的电路实现方法并不唯一,图8给出了式(1)另外一种实现电路。
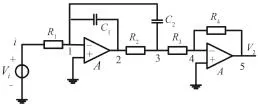
图8 Nomoto 模型另外一种等效电路Fig. 8 Another equivalent Nomoto model by circuit
由文献[1]给出的快速推导传递函数数学模型方法,该电路由 5个有效节点组成,有 2个放大器元件,分母中除了相互独立的 2个放大器元件回路项外,其他项都可省略,得到数学模型的过程如下:
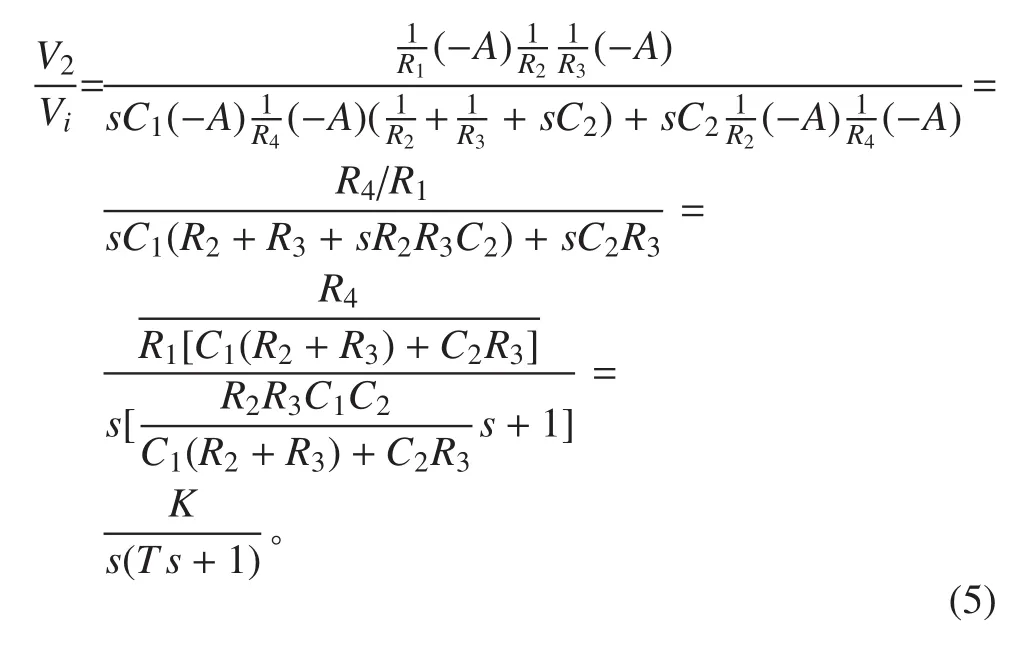
式中:
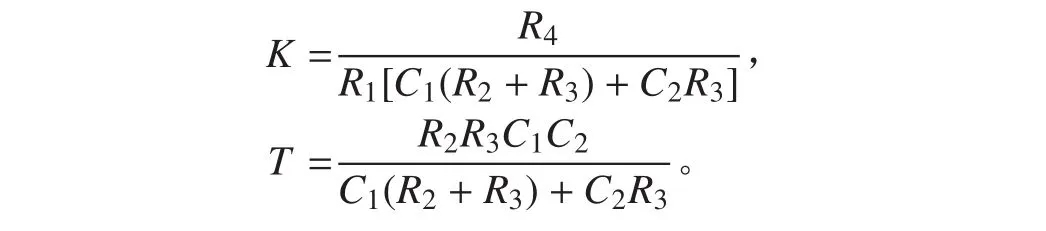
为了简化,令 R2=R3,C1=C2,则
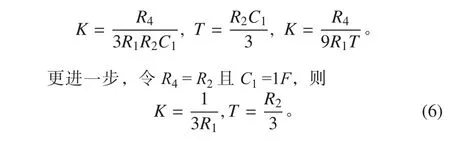
这样,任意船舶的等效数学模型的旋回性指数 K唯一由电阻 R1确定,追随性指数 T 唯一由电阻 R2确定,等效模型的构建变得更为简单。
设 R1=2 Ω,R2=347.4 Ω,即可得到与图7相同的仿真结果。
4 结 语
本文给出了 2种船舶 Nomoto 模型的电路网络实现形式,从理论上推导出的数学模型与 Nomoto 模型相同,使用 Matlab 仿真验证了其与实船试验结果符合度为86.8%。如果船舶 Nomoto 模型的 K,T 指数不做速度等影响的折合,则模型精度只能达到约 75%。下一步计划真正使用电路、电容和放大器元件搭建成电路板,然后使用仪器测量输出电压,进行相关的物理实验,结果将更直观。本研究使用电路软件仿真船舶模型,为进一步的半物理仿真打下理论基础。
[1]王贤惠, 纪致纹. 线性电工、电子及机械网络计算新法[M].大连: 大连海事大学出版社, 1997. WANG Xian-hui, JI Zhi-wen. A new method for calculating linear electrical, electronic and mechanical network[M]. Dalian: Dalian Maritime University Press, 1997.
[2]张显库, 金一丞. 控制系统建模与数字仿真[M]. 2版. 大连:大连海事大学出版社, 2013. ZHANG Xian-ku, JIN Yi-cheng. Modeling and digital simulation for control systems[M]. 2nd ed. Dalian: Dalian Maritime University Press, 2013.
[3]张显库. 船舶运动简捷鲁棒控制[M]. 北京: 科学出版社,2012. ZHANG Xian-ku. Concise robust control for ships[M]. Beijing: Science Press, 2012.
[4]ZHANG X K, ZHANG G Q, ZHANG S H, et al. Researches on the Williamson turn for very large carriers[J]. Naval Engineers Journal, 2013, 125(4): 129-137.
[5]ZHANG G Q, ZHANG X K. Concise robust adaptive path-following control of underactuated ships using DSC and MLP[J]. IEEE Journal of Oceanic Engineering, 2014, 39(4): 685-694.
[6]赵越. 欠驱动船舶水面的非线性数学模型及跟踪控制[J]. 舰船科学技术, 2015, 37(5): 192-195. ZHAO Yue. Nonlinear methematical model and tracking control study for underactuated marine surface vessels[J]. Ship Science and Technology, 2015, 37(5): 192-195.
[7]李晓君, 谢新连. 重大件运输的货物分配与航速联合优化[J].西南交通大学学报, 2015, 50(4): 747-754. LI Xiao-jun, XIE Xin-lian. Integrated optimization of cargo distribution and ship speed for heavy-cargo transportation[J]. Journal of Southwest Jiaotong University, 2015, 50(4):747-754.
[8]范爱龙, 严新平, 尹奇志, 等. 船舶主机能效模型[J]. 交通运输工程学报, 2015, 15(4): 69-76. FAN Ai-long, YAN Xin-ping, YIN Qi-zhi, et al. Energy efficiency model of marine main engine[J]. Journal of Traffic and Transportation Engineering, 2015, 15(4): 69-76.
[9]赵志强, 闫亚胜, 黄连忠, 等. 船舶翼帆回转速度的非线性补偿控制[J]. 哈尔滨工程大学学报, 2015, 36(10): 1346-1350. ZHAO Zhi-qiang, YAN Ya-sheng, HUANG Lian-zhong, et al. Nonlinear compensation of ship wing-sail slewing speed[J]. Journal of Harbin Engineering University, 2015, 36(10):1346-1350.
[10]张显库. 基于 Lyapunov 稳定性的船舶航向保持非线性控制[J]. 西南交通大学学报, 2010, 45(1): 140-143. ZHANG Xian-ku. Nonlinear control for ship course-keeping based on Lyapunov stability[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 140-143.
[11]哼之月. 有关如何让用matlab制作放大器[EB/OL]. (2012-11-21). http://blog.sina. com.cn/s/blog_a19f963501012ysl.html. HENG Zhi-yue. (2012-11-21). http://blog.sina.com.cn/s/ blog_a19f963501012ysl.html.
An equivalent Nomoto model of ships by circuit
ZHANG Xian-ku, YANG Guang-ping
(Navigation College, Dalian Maritime University, Dalian 116026, China)
In order to make the Nomoto model of ships visual, a circuit is built using resistances, capacitors and the amplifiers. The derived transfer function of circuit is the same as the Nomoto model of ships. An equivalent Nomoto model of Vessel Yukun by circuit is realized by appropriately choosing the parameters of circuit elements. The simulation results of circuit added speed loss compensation during turning, indicate that the model of circuit can be equivalent to the Nomoto model with satisfactory precision, comparing with the experimental results of real ship turning. And this has the important guiding significance to the semi-physical simulation of ship motion.
ship model;circuit;equivalent
U661.73
A
1672-7619(2016)09-0112-04
10.3404/j.issn.1672-7619.2016.09.023
2016-02-02;
2016-02-29
国家自然科学基金资助项目(51109020,51409033);中央高校基本科研业务费专项资金资助项目(3132014302)
张显库(1968-),男,教授,主要从事船舶运动控制及鲁棒控制研究。

