钢筋混凝土柱实验的OpenSEES建模参数敏感性分析

王　涛，　孙　严，　孟丽岩，　薛志成，　杜文学

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)



钢筋混凝土柱实验的OpenSEES建模参数敏感性分析

王涛，孙严，孟丽岩，薛志成，杜文学

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

利用OpenSEES进行结构建模时，需要人为定义单元及模型参数。为了验证参数取值对数值模拟结果精度的影响，以清华大学钢筋混凝土框架结构盲测实验中的中柱拟静力实验为对象，进行基于两端塑性铰单元建模参数敏感性分析。结果表明：塑性铰长度Lp和箍筋约束引起的核心区混凝土强度增强系数K对模拟精度有较大影响，并分别给出Lp和K的取值建议。该研究可以为OpenSEES建模提供参考。

OpenSEES； 两端带塑性铰单元； 纤维模型； 滞回曲线

数值模拟是一种再现结构弹塑性地震反应的主要手段，目前，数值模拟结果与实验结果仍存在一定差距[1-2]。数值模拟结果的误差来源有多方面原因：一是目前结构弹塑性分析理论上存在不足；二是使用者在有限元模型的选择及模型参数确定上仍存在困难。

OpenSEES是一种源代码公开的开放式结构分析软件，集合了较新的科研成果，受到研究者们及工程界的广泛关注。单元模型包括非线性梁柱单元、基于位移法的梁柱单元、两端带塑性铰单元[3-4]。文献[5]针对基于位移法的梁柱单元进行建模参数敏感性分析。

笔者针对清华大学实验中的中柱C和中柱D，分别采用两端带塑性铰的梁柱单元进行建模，分析塑性铰长度和截面核心区混凝土强度提高系数K对模拟精度的影响规律。

1　单元模型与实验

1.1两端塑性铰单元

两端塑性铰单元假定塑性变形集中在单元两端，单元中间部分为弹性变形，如图1所示。两端塑性铰单元通过对塑性区塑性铰长度、控制截面定义来模拟整个结构的非线性反应[6]。在每一端塑性区设置一个积分控制截面，塑性区控制截面采用纤维截面，纤维同样采用材料的单轴本构。

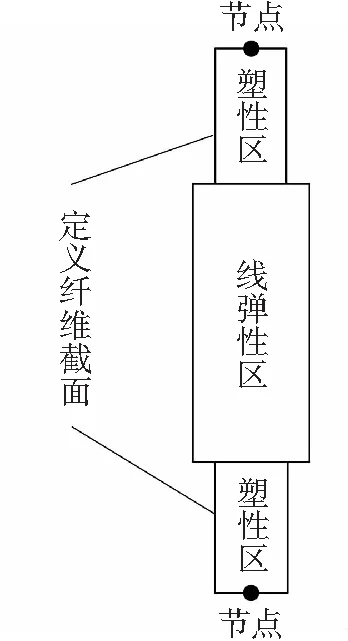
图1　两端塑性铰单元示意

1.2实验

钢筋混凝土框架结构中柱C、中柱D的拟静力实验得到的滞回曲线分别如图2a和图2b所示[2]。

2　钢筋混凝土柱的数值模拟

2.1基于中柱C对塑性铰长度分析

1992年,Paulay和Priestley[7]考虑了纵筋黏结滑移和应变渗透对模拟结果的影响，修正塑性铰长度Lp表达式为

Lp=0.08L+0.022dbfy，

(1)

式中：L——柱反弯点到最大弯矩截面的距离；

db——纵筋直径；

fy——纵筋屈服强度。

2008年，Sungjin Bae[8]提出基于混凝土压应变方法来估计柱的塑性铰长度，塑性铰长度表达式为

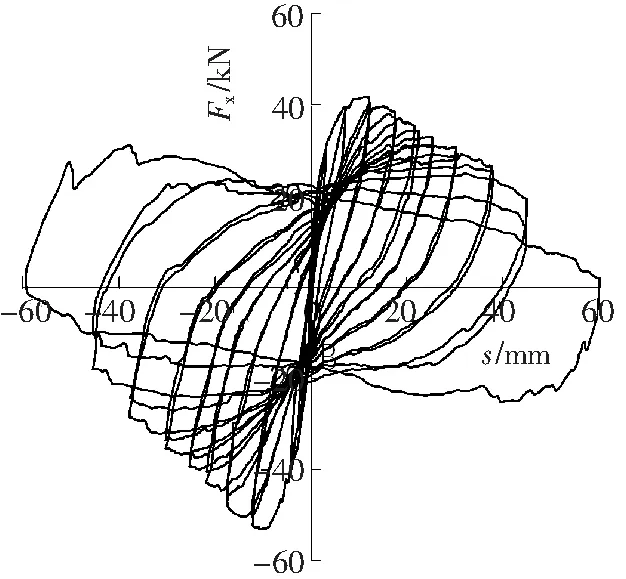
a　中柱C

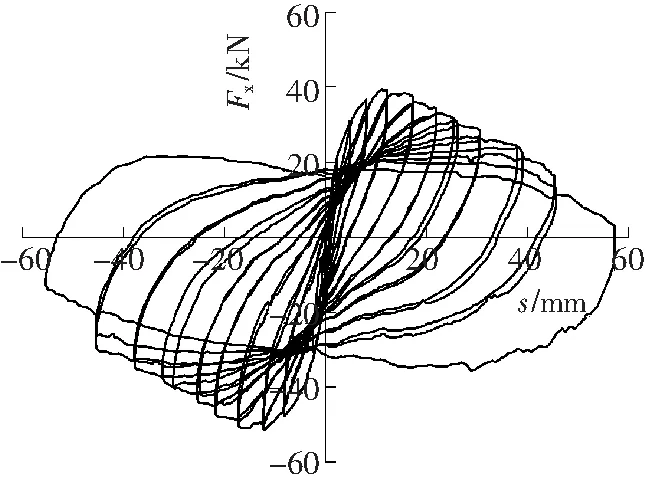
b　中柱D

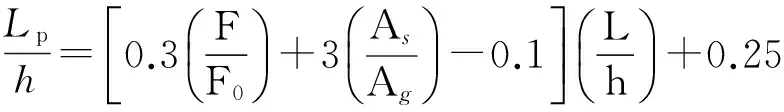
(2)

式中：h——柱截面高度；

F——轴向力；

Ag——柱截面面积；

As——受拉纵筋面积。

F0定义为

(3)

按照式(1)和式(2)计算得到的塑性铰长度分别为165和57 mm。各国学者对塑性铰长度计算提出许多经验公式，适用于柱的塑性铰长度Lp在0.5h～1.0h[9]。可见，目前塑性铰长度的取值并没有比较统一认可的建议。文中分别选取塑性铰长度57、110、165、180、220 mm进行建模，相应的模拟结果分别对应图3a～3e所示。

通过图3a和图3c比较，对于该构件基于式(1)计算得到的塑性铰长度明显好于基于式(2)计算得到的塑性铰长度。式(1)中影响塑性铰长度的因素包括反弯点到最大弯矩截面的距离、纵筋直径、纵筋屈服强度，而中柱D和C的这些参数均相同，因此,对于中柱D可以采用与中柱C相同的塑性铰长度。

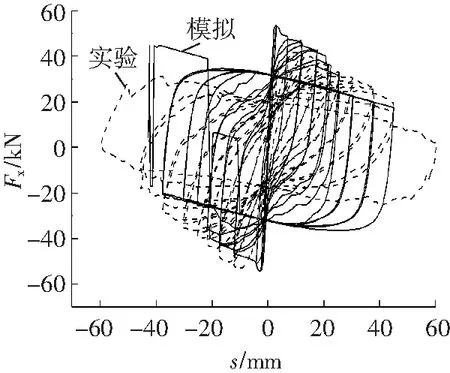
a　Lp=57 mm

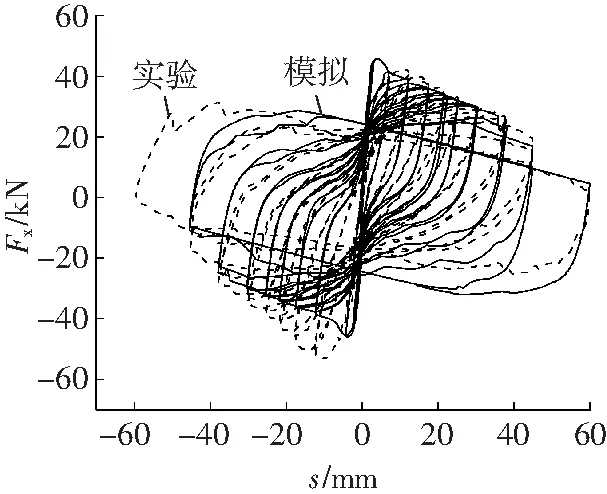
b　Lp=110 mm

c　Lp=165 mm

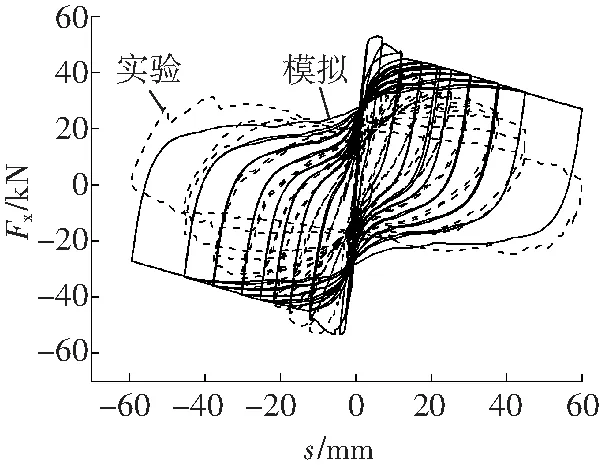
d　Lp=180 mm

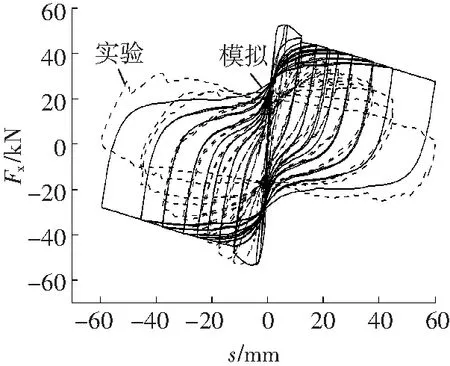
e　Lp=220 mm

为了评价数值模拟得到的滞回曲线和实验测得的滞回曲线相近程度，采用相关系数作为一种定量的评价指标[10]，即

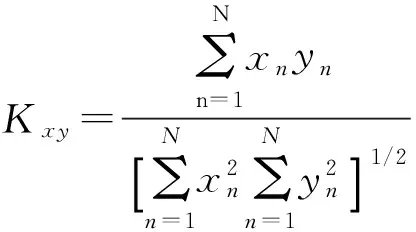
(4)

式中：xn——恢复力实验测量值；

yn——恢复力数值模拟值；

N——实验加载步数；

Kxy——相关系数，是一种量纲为一指标，该值越接近1就表示两组曲线的近似程度越高。

相关系数Kxy也可定量评价在不同参数设定情况下模拟结果的精度。

为了方便绘制相关系数与不同塑性铰长度变化关系，塑性铰长度为57、110、165、180、220mm时，分别按方案1、2、3、4、5来进行分析。由于方案1、方案2,部分加载位移下的水平力模拟失败，故暂不考虑方案1、方案2对应的相关系数。方案3、方案4、方案5对应的相关系数如图4所示。

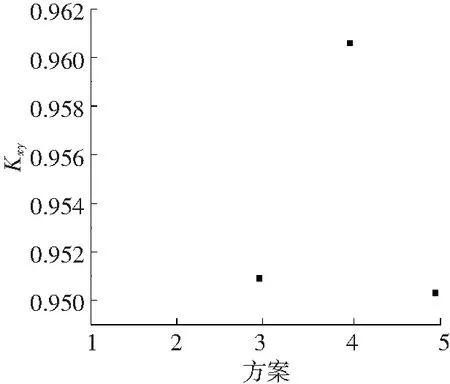
图4　不同塑性铰长度方案对应的相关系数

通过图4得出，塑性铰长度Lp=180 mm时，对应相关系数明显大于Lp=165 mm、Lp=220 mm时对应的相关系数。因此，对于中柱C和中柱D塑性铰长度均取为180 mm。为了提高数值模拟精度，对塑性铰长度的理论值计算式(1)进行简单修正，在原公式中增加了增大系数η：

Lp=η(0.08L+0.022dbfy)，

(5)

式(5)中增大系数η为修正后与修正前塑性铰长度的比值，可取η=180/165=1.091。

2.2基于中柱C对K分析

在进行模型建立时，混凝土材料模型选用基于Kent-Park模型定义参数的单轴本构材料Concrete01[11]。Kent-Park模型能反应配箍特征值和箍筋间距对约束混凝土的影响。Concrete01模型受约束区混凝土的本构关系调整为：

当εc≤0.002K时，则

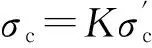
(6)

当εc>0.002K时，则

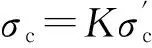
(7)

且

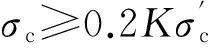
(8)

式(6)、(7)中，εc为约束混凝土峰值应变；K为箍筋约束引起的混凝土强度增强系数，K定义为

(9)

式中:fyh——箍筋屈服强度,MPa；

ρs——试件的体积配箍率。

式(7)中，Zm为混凝土应变软化段斜率，定义为

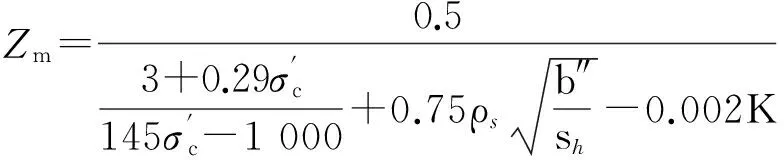
(10)

式中:b″ ——从箍筋外边缘算起的核心混凝土宽度；

sh——箍筋间距。

保护层区混凝土极限应变默认为0.004；核心区混凝土脱落失效时应变εmax确定为

(11)

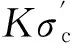
下面针对C柱的拟静力实验进行数值模拟，以检验式(9)的有效性。

由式(9)计算得到混凝土强度增强系数理论值K=1.281 1，模拟结果如图5所示。同时，将K分别取1.2、1.4、1.5、1.6、1.7、1.8进行建模，相应的模拟结果分别对应图6所示。

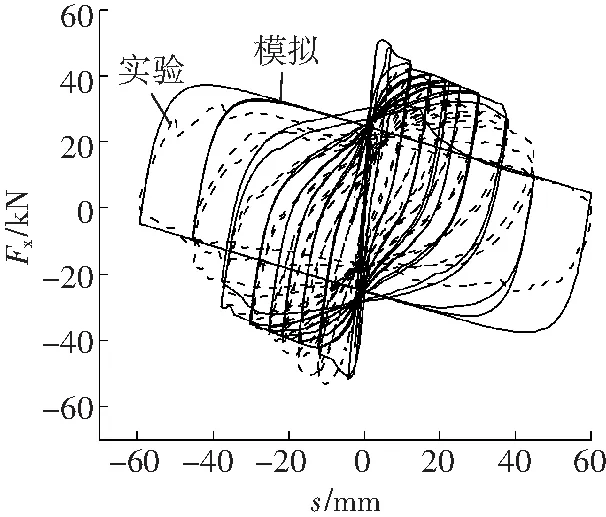
图5　K=1.281 1时C柱滞回曲线对比

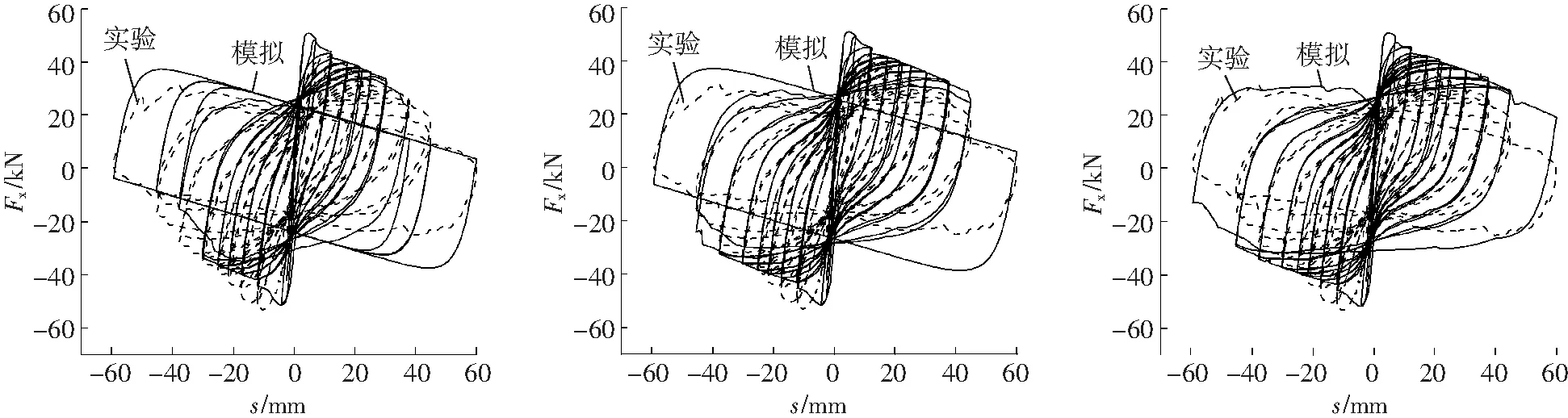
a　K=1.2　　　　　　　　　　　　　　　　b　K=1.4　　　　　　　　　　　　　　　　c　K=1.5

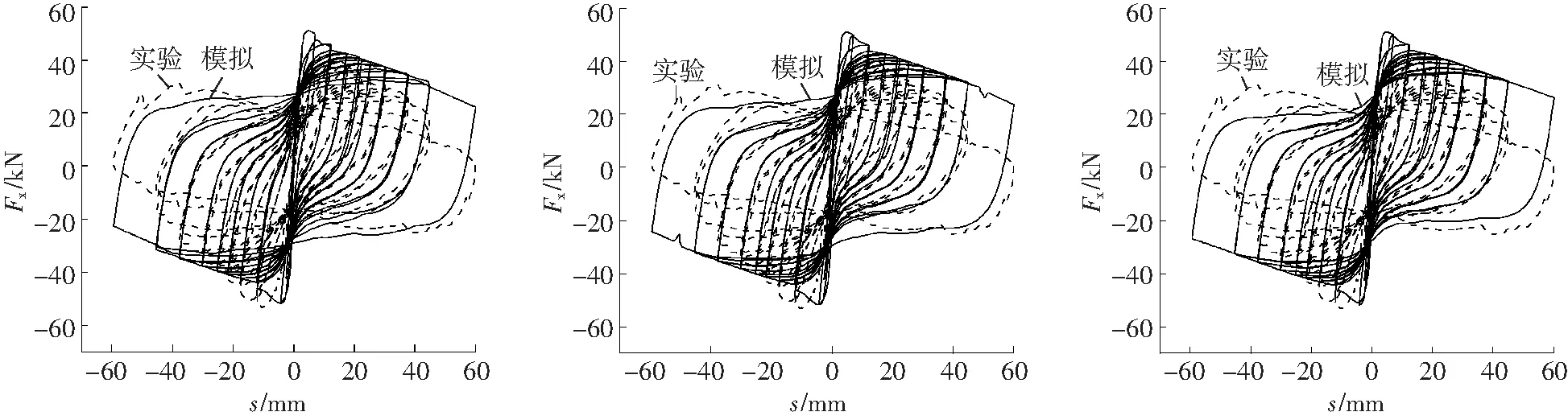
d　K=1.6　　　　　　　　　　　　　　　　e　K=1.7　　　　　　　　　　　　　　　　f　K=1.8

图7为C柱采用不同K值的相关系数曲线。由图7可以看出，K取值不同，数值模拟的滞回曲线形状和走势发生了明显变化。随着K值的增加，滞回曲线会变得更加丰满，耗能能力增强，同时模拟结果与实验结果的差距也逐渐加大。为了定量评价K对数值模拟精度的影响，图7给出了K取不同值所对应的相关系数。可以看出，取理论值K=1.281 1时的相关系数为0.962 8，而在K=1.4时相关系数取得最大值0.972 9。当K<1.4时， 相关系数随着K值单调递增，当K>1.4时，相关系数随着K值单调递减。与K的理论值相比，K取1.4为K理论值的1.09倍，模拟结果的相关系数提高了1.05%。

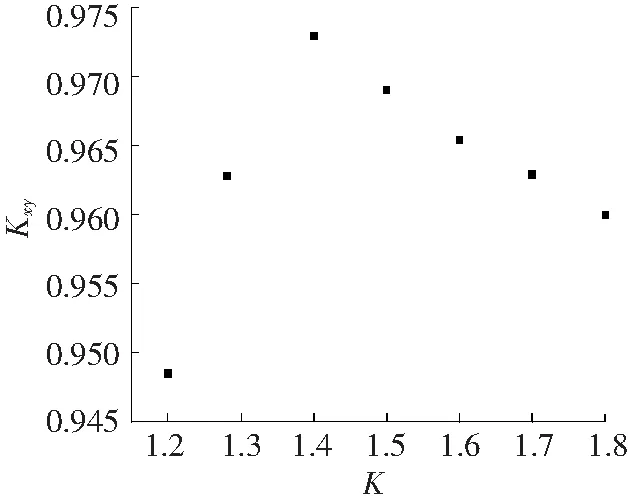
图7　C柱采用不同K值的相关系数

2.3基于中柱D对K分析

下面针对中柱D的拟静力实验进行数值模拟，以检验式(9)的有效性。塑性铰长度取Lp=180 mm。由式(9)计算得到的混凝土强度增大系数理论值为K=1.260 4，数值模拟结果如图8所示。将K分别取值1.1、1.4、1.5、1.6、1.7、1.8进行建模，相应的模拟结果分别对应图9所示。

从图9可以看出，K取值不同，数值模拟的滞回曲线形状和走势依然发生了明显变化。随着K值的增加，滞回曲线会变得更加丰满，耗能能力增强。K取较小值和较大值时，模拟结果均与实验结果的差距较大。

图10为不同K值的相关系数曲线。图10表明，相关系数随着K增大开始增大，然后减小。K取理论值1.260 4时的相关系数为0.915 1，K=1.5时相关系数取得最大值0.950 2。与K的理论值相比，K取1.5为K理论值的1.19倍，模拟结果的相关系数提高了3.84%。

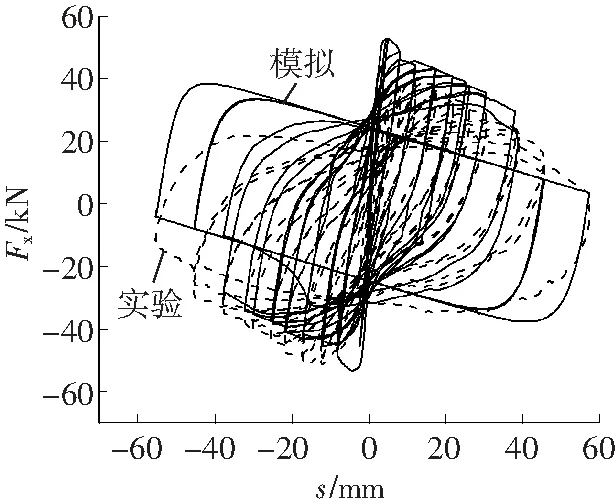
图8　K=1.260 4时D柱滞回曲线对比

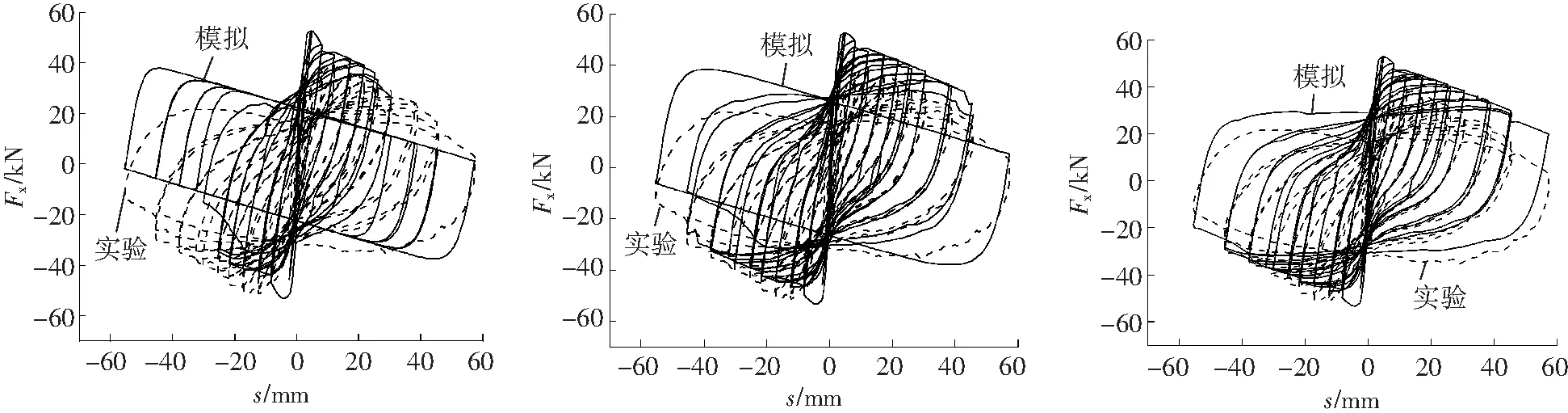
a　K=1.1　　　　　　　　　　　　　　　b　K=1.4　　　　　　　　　　　　　　　c　K=1.5

d　K=1.6　　　　　　　　　　　　　　　e　K=1.7　　　　　　　　　　　　　　　f　K=1.8

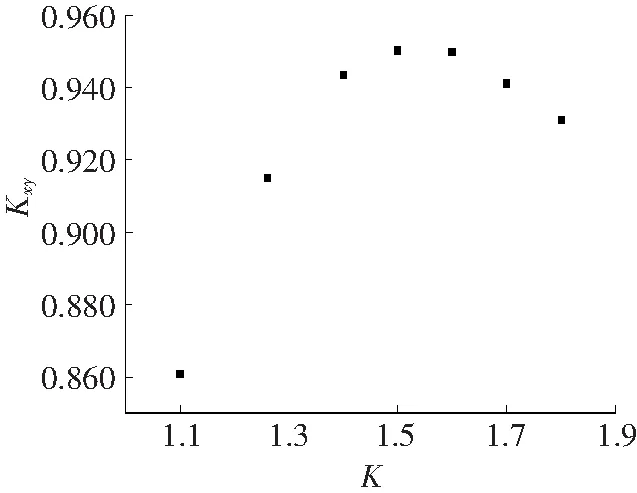
图10　D柱采用不同K值的相关系数

为了提高数值模拟精度，对K的理论值计算式(9)进行简单修正，在原公式中增加了一个K值增大系数ξK：

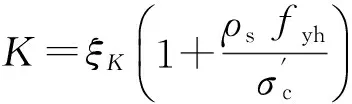
(12)

根据对C柱和D柱的上述数值模拟结果，K值增大系数ξK建议取两次数值模拟最好结果时的K值增大倍数的平均值，即

ξK=(1.19+1.09)/2=1.14。

(13)

3　结　论

利用钢筋混凝土柱拟静力实验数据，基于两端塑性铰单元进行了建模参数的敏感性分析，得到如下结论：

(1)塑性铰长度对模拟结果精度影响较大，基于式(1)提出了修正的塑性铰长度Lp表达式，建议Lp增大系数η取值为1.091。

(2)箍筋约束引起的核心区混凝土强度增强系数K对模拟结果的影响较大，提出了修正的强度增强系数K表达式，建议K值增大系数ξK取为1.14。

[1]中国建筑学会建筑结构防倒塌专业委员会. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅲ: 模拟结果分析[J]. 建筑结构， 2012, 42(11): 27-30.

[2]陆新征， 叶列平， 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅱ: 关键构件试验[J]. 建筑结构， 2012, 42(11): 23-26.

[3]宁超列， 段忠东. OpenSEES中三种非线性梁柱单元的研究[J]. 低温建筑技术， 2009, 31(3): 49-52.

[4]许建立， 余琼， 刘金成. 基于OpenSEES的RC梁柱组合件低周反复试验数值模拟[J]. 结构工程师, 2013, 29(2): 82-87.

[5]王涛， 孙严， 孟丽岩. 基于OpenSEES的RC柱拟静力实验数值分析[J]. 黑龙江科技大学学报， 2016， 26(1)： 89-94.

[6]凌炯. 面向对象开放程序OpenSEES在钢筋混凝土结构非线性分析中的应用与初步开发[D]. 重庆: 重庆大学， 2004： 13-20.

[7]PAULAY T, PRIESTLEY M J N. Seismic design of reinforced concrete and masonry buildings [M]. New York: John Whey & Sons, 1992.

[8]BAE S , BAYRAK O. Plastic hinge length of reinforced concrete columns[J]. Aci Structural Journal， 2008, 105(3)： 290-300.

[9]MEHMET I, BAYTAN O H. Effects of plastic hinge properties in nonlinear analysis of reinforced concrete buildings[J]. Engineering Strutures, 2008, 28(11): 1494-1502.

[10]刘永昌， 关淑贤， 任贵兴， 等. 地震模拟振动台波形再现定量判别法[J]. 地震工程与工程振动， 1998, 18(1): 109-112.

[11]SCOTT B D， PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. Aci Journal, 1982, 79(1): 13-27.

(编辑徐岩)

Sensitivity analysis of modeling parameters for OpenSEES based on reinforced concrete columns tests

WANGTao,SUNYan,MENGLiyan,XUEZhicheng,DUWenxue

(School of Civil Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

The OpenSEES is an open structure nonlinear analysis software combining the latest research development which has received a wider attention from researchers and engineering area. Structure modeling forces an artificial definition of parameters of elements and model. The verification of the effect of parameters on simulation accuracy builds on the quasi-static test of the middle columns involved in the blind experiment of reinforced concrete frame structures in Tsinghua University and a resultant analysis of modeling parameters sensitivity for the displacement-based beam-column element. The results show that the hinges lengthLpand the strength enhancement coefficientKof the core concrete caused by stirrup constrains have obvious influence on simulation results. The recommended value ofLpandKare given. The study can provide useful reference for structure modeling using the OpenSEES.

OpenSEES； beam with hinges element； fiber model； hysteretic curves

2015-09-30

黑龙江省自然科学基金项目(QC2013C055);国家自然科学基金项目(51408157;51308159;51308160)

王涛(1978-)，男，黑龙江省集贤人，副教授，博士，研究方向：结构地震反应分析、结构抗震实验方法与技术，E-mail: hitwangtao@126.com。

10.3969/j.issn.2095-7262.2016.02.023

TU398.7

2095-7262(2016)02-0224-06

A