联合新型分块稀疏表示和梯度先验图像盲复原
杨爱萍,梁 斌,何宇清,张莉云,魏宝强
(天津大学电子信息工程学院,天津 300072)
联合新型分块稀疏表示和梯度先验图像盲复原
杨爱萍,梁 斌,何宇清,张莉云,魏宝强
(天津大学电子信息工程学院,天津 300072)
针对目前基于稀疏表示的图像盲复原算法计算量大且细节恢复能力有限等问题,提出一种新的图像盲复原方法.首先针对现有稀疏表示模型中重叠分块计算复杂度高的问题,提出一种多模式非重叠分块策略,在每种模式下独立求解复原图像,然后对各模式下复原图像求平均以消除“伪像”;另外,用范数作为稀疏性度量,将图像梯度稀疏先验融入基于稀疏表示的图像盲复原模型.最后,本文提出了联合新型分块字典稀疏表示和图像梯度稀疏先验的盲复原模型,采取迭代方法交替估计模糊核和待复原图像.实验结果表明,该方法在主观和客观评价下均取得较好的复原结果,并显著降低算法整体复杂度.
盲复原;新型分块字典稀疏表示;梯度稀疏先验
图像复原是典型的病态逆问题,根据模糊核是否已知可将图像复原算法分为两大类:一类是当模糊核已知时,称为非盲复原问题,如维纳滤波[1]和RL算法[2]是两种最常见的非盲复原方法;另一类是当模糊核未知时,称为盲复原问题,需要从退化图像中同时估计出模糊核和原始图像.
近年来,图像盲复原技术成为研究的热点,学者们提出了一系列有效算法.其中一类方法基于自然图像梯度的稀疏性先验而提出,Fergus等[3]提出变分贝叶斯方法,对图像梯度的重尾分布用混合高斯模型进行建模.Krishnan等[4]使用la(a=0.5~0.8)范数度量稀疏性对图像进行约束,提高了对自然图像梯度重尾分布的拟合度.在此基础上,Krishnan等[5]提出了基于l1/l2范数的稀疏性度量,保证算法收敛于全局最优解.这些方法取得了很好的复原效果,但都需要求解反卷积问题,导致算法不稳定且计算量大.
随着稀疏表示理论的发展,基于字典稀疏表示[6-7]的图像盲复原方法取得了一系列进展.Hu等[8]提出一种基于自适应字典学习的图像盲去模糊算法,但该算法仅适用于小的核模糊,对于大的核模糊图像复原效果很差.Zhang 等[9]提出基于稀疏表示的图像盲去模糊算法,但因对图像块进行字典稀疏表示与重构,导致复原后图像块连接构成整幅图像时产生“伪像”,影响图像整体复原效果.Jia等[10]联合字典稀疏表示和空域约束,以及Li等[11]引入正则化规范,均取得了不错的复原效果,但对细节的恢复能力有限,仍需进一步改进.
笔者针对目前基于稀疏表示的盲复原算法中存在的计算复杂度高、细节恢复能力有限、易产生“伪像”等不足,结合字典稀疏表示和图像梯度先验约束,提出了一种新的图像盲复原算法.主要包括:为了降低算法的复杂度,引入一种新的图像非重叠分块方式,并利用高效的稀疏编码方法,提高训练字典的自适应性和编码的有效性;融入新的图像稀疏先验和模糊核先验,构造新的代价函数.实验结果表明,本文方法可有效克服目前算法中普遍存在的缺陷.
1 基于稀疏表示的图像盲复原
1.1图像盲复原问题
图像模糊退化过程可建模如下:

式中:x和y分别为原始清晰图像和模糊图像字典排列的向量形式;k为模糊核或点扩散函数;n为加性高斯白噪声;*为卷积运算符.由此可知,图像复原过程即为由模糊加噪图像y估计清晰图像x的过程.当未知量个数小于已知变量个数时,图像盲复原是典型的欠定问题,需要利用正则化方法融入图像的先验信息以得到稳定解,常表示为如下最优化问题:

式中:ρ(x)为正则化项,常基于自然图像的先验信息而给定[12-14];φ(k)为模糊核先验正则化项;μ和β分别为图像先验和模糊核正则化参数,μ≥0,β≥0.
1.2基于稀疏表示的图像盲复原模型
在稀疏模型中,图像通常被分解成很小的块进行稀疏表示和重构[15].对于给定的图像x∈Rn,令为图像块提取矩阵,则每个图像块可表示为

如果图像块xi具有稀疏性,则xi可由过完备字典D∈Rn×L(n<L)的原子进行线性表示,即

式中:字典D每1列称为1个原子;αi为图像块xi在字典D下的稀疏表示系数.整幅图像可表示为

由式(2)可知,基于稀疏表示的图像盲复原模型可表示为

式中:Ri为提取图像的第i块的矩阵;公式右边第1项为保真项,确保恢复的图像与原始清晰图像尽可能地接近;第2和第3项为图像块在过完备字典D下的稀疏表示;ξi和ψi分别为字典表示和稀疏系数向量参数,ξi≥0,ψi≥0;第4项为模糊核约束项.
1.3现有分块模式的缺陷
如前所述,在稀疏表示模型中,图像通常被分解成很小的块进行稀疏表示和重构.为了降低复原图像的块效应,目前通常采用重叠取块方式,如图1所示.这种重叠取块方式可在一定程度上抑制复原图像的块效应,但需要对每一块进行稀疏表示.一方面,相邻的块具有相似特征,会产生过多无用的稀疏系数;另一方面,需要对每一块进行复原计算,大大增加了算法的复杂度,而且恢复的图像常常出现“伪像”[9].

图1 图像重叠取块方式Fig.1 Method of overlapping image patches
另外,目前基于稀疏表示的图像盲复原框架中,对图像先验的约束常采用l1范数进行稀疏性度量.由文献[5]可知,l1范数仅适用于图像去噪,对于图像复原问题,采用可取得更好的结果.因此,为解决上述问题,本文提出基于非重叠分块稀疏表示的图像盲复原框架,并将作为稀疏性度量,提出新的盲复原模型.
2 本文算法
2.1不同模式下的非重叠分块
重叠取块会产生过多无用的稀疏系数且大大增加了算法的复杂度,特别是当图像尺寸较大时,问题尤为严重.在不降低复原图像质量的前提下,为了解决这一问题,本文采用一种新的非重叠分块方式,如图2所示.

图2 图像非重叠取块方式Fig.2 Method of non-overlapping image patches
由于这种非重叠取块方式要求相邻图像块之间没有重叠区域且这些块必须包含图像的每个像素点,所以图像可能不被均匀分割,即提取图像块的尺寸可能不相同.基于这一现象,本文将图像按照几种不同的模式进行非重叠分块.例如,将一个大小为N1×N2的图像按照块尺寸n1×n2进行分块.为便于说明,现将图像块类型分为内部块、边界块和拐角块,并规定所有的图像块水平和垂直对齐.
(1) 内部块.如图3中标记为1的块,块尺寸为n1×n2.
(2) 边界块.如图3中标记为2的块,若在图像左边界和右边界,则行数为n1,列数小于n2;若在图像上边界和下边界,则列数为n2列,行数小于n1.
(3) 拐角块.如图3中标记为3的块,块的尺寸小于n1×n2.
根据上述规定,图像的非重叠取块方式可以由图像左上角块的尺寸唯一确定,如图3所示60× 60的图像,在3种模式下进行的8× 8非重叠分块.取图像左上角块大小分别为4× 8、8× 4和8× 2,并依据上述规定进行划分,可以看出3幅图像提取块的边界位于不同的像素点.

图3 3种非重叠块分割Fig.3 Three different ways of non-overlapping patches
在上述每种非重叠分块模式下,求解基于稀疏表示的图像盲复原问题模型.在每种独立分块模式下,复原图像会在分块边界处产生明显的块效应,为了解决该问题,本文采用在多种分块模式下独立求解复原图像,然后再总体求算术平均的方式.后续实验验证了该方法,能有效抑制“伪像”效应,提高PSNR值,且大大降低算法的复杂度.
2.2基于非重叠分块字典稀疏表示和梯度先验的图像盲复原
自然图像的梯度直方图服从一种典型的重尾分布[3],算法通常采用图像的l1范数或la(a=0.5~0.8)范数作为稀疏性度量.由文献[5]可知,这些范数在代价函数求解过程中,图像高频区域反而变得更加模糊,纹理细节无法有效得到复原.


式中:公式右边第4项为图像梯度约束项;∇x为图像在水平和垂直方向上的梯度,采用作为稀疏性度量范数,可以有效地提高图像的复原能力;最后一项为模糊核约束项,选用l1范数进行约束,同时核满足归一化和非负值;ηi、λi、ρ、γi为平衡各项之间的参数.
3 模型的求解
稀疏表示中,字典D起着至关重要的作用,其原子与图像特征的匹配程度直接影响着图像复原的质量.本文采用文献[16]提出的块邻域梯度字典学习(block proximal gradient,BPG)算法对Berkeley Segmentation Dataset[17]中200幅图像随机提取20,000个8× 8图像块进行学习得到需要的字典.BPG算法相比之前的KSVD算法[17]和OLM算法[18]等,具有更快的收敛速度和更强的自适应性.
式(7)中存在3个未知量:模糊核k、稀疏系数向量α、清晰图像x,直接求解将面临收敛慢速和容易陷入局部最小值等问题,本文采取交替更新的方法进行求解.分别固定其中两个未知量,每次只求解1个参数,因此每一个迭代过程,将式(7)转化成多个简单的子问题.
3.1k-子问题:模糊核估计
该子问题中,固定系数α和图像x,求图像的模糊核k,式(7)可简化为

这里采用在梯度域通过迭代收缩软阈值ISTA算法对式(8)进行求解,求解过程可分两步进行.首先求得约束下的梯度图像∇x,然后通过梯度图∇x、∇y估计模糊核k,因此,式(8)可分解为
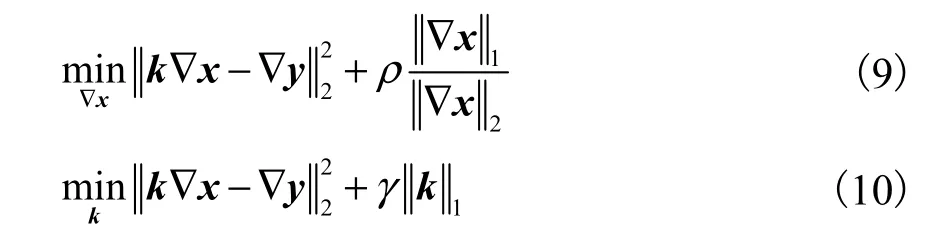
式中∇x、∇y分别为待复原图像和模糊图像在水平和垂直方向上的梯度.
这里可将式(9)中梯度的范数l2看作已知量,即则式(9)可转化为范数l2与l1相加的形式,即

式(11)即可采用迭代收缩软阈值ISTA算法求解,求得图像的模糊核k,具体步骤如表1所示.

表1 模糊核k更新Tab.1 Kernel updating
3.2x-子问题:清晰图像估计
当模糊核k和稀疏系数向量α固定时,可将式(7)简化为

该子问题为最小二乘问题,可利用快速傅里叶变换(FFT)求解[14],其解形式为

式中:F(·)为傅里叶变换;F-1(·)为F(·)的逆变换;为F(·)的共轭;°表示矩阵对应元素相乘.
在每种非重叠分块模式下,分别得到清晰图像的1个估计,即

通过多次实验测试发现,对图像进行3种模式的非重叠分块即可有效抑制复原图像的块效应,过多模式的分块对改善“伪像”影响不大,且会降低算法的效率,因此,本文采取3种非重叠分块方式估计清晰图像.
3.3α-子问题:稀疏系数估计
当估计得到的图像x及模糊核k固定时,式(7)可简化为

式(15)中,图像块之间是相互独立的,可以转化为各图像块的稀疏系数求解问题,即

为了提高稀疏表示效率,平衡所有系数对最优解的影响,式(16)利用加权l1范数优化算法.加权l1范数通过对图像的平滑区域和边缘采用不同的权重来提升细节恢复能力,在实际中获得了广泛的应用.这里采用稀疏系数的反函数形式,并为了确保权系数恒大于0,采用如下形式:

利用文献[19]中的YALL1算法求解加权l1范数最优化问题(即式(16)).
本文提出的基于新型分块字典稀疏表示和梯度先验的快速图像盲复原算法具体步骤如表2所示.

表2 算法的整体思路Tab.2 Overall algorithm
4 实验结果及分析
为了验证本文所提算法的有效性,选取Levin图像集中的16幅测试图像[20]和2幅实拍模糊图像[5],分别进行盲复原实验.
首先,针对测试图像进行实验.实验对象选取模糊核分别为7× 7、13× 13、17× 17以及23× 23的高斯模糊图像,并添加方差为0.01的加性高斯白噪声.稀疏模型中选取图像块为8× 8;式(7)中各参数取值依次为:η=0.05、λ=0.1、ρ=0.15、γ=4.6.将本文提出的算法与近年来公认较为优秀的单幅图像盲复原算法(Levin和Babacan的空域复原方法[21-22]、Hu等[8]的稀疏域复原方法)进行比较,计算复原图像与原图像的峰值信噪比(PSNR),计算结果如表3所示.由表3可看出,本文提出的基于新型分块字典稀疏表示和梯度先验的盲复原方法取得了较高的PSNR值.

表3 几种算法盲复原结果比较Tab.3Comparison of blind recovered results with different algorithms
图4和图5给出了复原图像效果及估计的模糊核.由图可看出,Levin算法和Babacan算法对模糊核的估计比较准确,复原图像能够恢复出一定的细节,但是相比于原始清晰图像感觉有一层“薄雾”覆盖在图像上方;Hu的算法适用于模糊核尺寸不超过9× 9的图像盲复原[8],当尺寸较大时,对模糊核估计不准确,造成图像复原效果较差;本文方法可准确估计较大尺寸模糊核,且复原图像细节清晰,主观效果较好.

图4 Building复原效果比较Fig.4Recovered results of Building with different algorithms

图5 Children复原效果比较Fig.5 Recovered results of Children with different algorithms
下面对本文算法的复杂度进行讨论.上述几种算法中,Levin和Babacan的算法是在空域进行的,本文研究稀疏表示框架下图像盲复原问题,因此这里对相同条件下的Hu算法[8](重叠5像素)、传统重叠分块稀疏表示(重叠4像素)、本文非重叠分块稀疏表示下算法(式(7))的运行时间进行比较.实验中选取预先学习得到的字典,计算相同迭代次数下的稀疏编码、复原图像和估计模糊核3个子问题的总运行时间,分别对高斯模糊核为7× 7、13× 13和23× 23 3种图像盲复原时间进行统计,结果如表4所示.由表3、表4可以看出,本文提出的基于新型分块模式算法在较好改善图像复原质量的前提下,能有效降低算法的运行时间.
最后,为了进一步验证本文算法的有效性,对几幅实拍模糊图像进行盲复原实验,选取了盲复原算法中常用未知模糊核的“鱼”和“佛”实拍图像[5],复原效果如图6和图7所示.由图6和图7可以看出,所提算法对高斯模糊之外的实际拍摄的模糊图像也具有很好的复原效果.

图6 鱼复原效果比较Fig.6 Recovered results of Fish with different algorithms

图7 佛复原效果比较Fig.7 Recovered results of Buddha with different algorithms
5 结 语
针对现有基于稀疏表示的图像盲复原方法中计算量大且恢复细节有限等问题,本文采用一种新的非重叠分块方式降低算法的复杂度,并利用新型的稀疏编码算法提高字典的自适应性和编码的有效性.另外将作为稀疏性度量范数融入总的代价函数,提出新的盲复原模型.实验结果表明,本文提出的盲复原算法在保证改善图像复原质量的同时,大大降低了算法的整体复杂度.
[1] Wiener N. Extrapolation,Interpolation,and Smoothing of Stationary Time Series [M]. Cambridge:MIT Press,1964.
[2] Lucy L B. An iterative technique for the rectification of observed distributions [J]. Astronomical Journal,1974,79(6):745-754.
[3] Fergus R,Singh B,Hertzmann P. Removing camera shake from a single photograph [J]. ACM Transactions on Graphics,2006,25(3):787-794.
[4] Krishnan D,Fergus R. Fast image deconvolution using hyper-Laplacian priors [C]//Advances in Neural Information Processing System. Vancouver,Canada,2009:1033-1041.
[5] Krishnan D,Tay T,Fergus R. Blind deconvolution using a normalized sparsity measure [C]//IEEE International Conference on Computer Vision and Pattern Recognition. Colorado,USA,2011:233-240.
[6] 杨爱萍,钟腾飞,何宇清. 基于非局部相似性和分类半耦合字典学习的超分辨率重建[J]. 天津大学学报:自然科学与工程技术版,2015,48(1):87-94. Yang Aiping,Zhong Tengfei,He Yuqing. Superresolution reconstruction based on non-local similarity and clustered semi-coupled dictionary learning [J]. Journal of Tianjin University:Science and Technology,2015,48(1):87-94(in Chinese).
[7] 程广涛,宋占杰,陈 雪. 基于二维图像矩阵的稀疏表示分类方法[J]. 天津大学学报:自然科学与工程技术版,2014,47(6):541-545. Cheng Guangtao,Song Zhanjie,Chen Xue. Classification based on sparse representation with two dimensional image matrix [J]. Journal of Tianjin University:Science and Technology,2014,47(6):541-545(in Chinese).
[8] Hu Z,Huang J B,Yang M H. Single image deblurring with adaptive dictionary learning[C]// IEEE International Conference on Image Processing. Piscataway,NJ,United States,2010:1169-1172.
[9] Zhang H,Yang J,Zhang Y,et al. Sparse representation based blind image deblurring [C]// IEEE International Conference on Multimedia and Expo. Barcelona,Spain,2011:1-6.
[10] Jia C,Evans B L. Patch-based image deconvolution via joint modeling of sparse priors [C]// IEEE International Conference on Information Processing. Brussels,Belgium,2011:681-684.
[11] Li H,Zhang Y,Zhang H,et al. Blind image deblurring based on sparse prior of dictionary pair [C]// IEEE International Conference on Pattern Recognition. Tsukuba,Japan,2012:3054-3057.
[12] Roth S,Black M J. Fields of experts:A framework for learning image priors [C]// IEEE International Conference on Computer Vision and Pattern Recognition. Boston,USA,2005:860-867.
[13] Taeg S C,Joshi N,Zitnick Z L,et al. A content-aware image prior [C]// IEEE International Conference on Computer Vision and Pattern Recognition. San Francisco,USA,2012:3054-3057.
[14] Shan Q,Jia J Y,Agarwala A. High-quality motion deblurring from a single image [J]. ACM Transactions on Graphics,2008,27(3):1-10.
[15] Elad M,Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing,2006,15(12):3736-3745.
[16] Xu Yangyang,Yin Wotao. A Fast Patch-Dictionary Method for Whole Image Recovery. CAM-Report-13-38[R]. Los Angeles,CA:UCLA,2013.
[17] Aharon M,Elad M,Bruckstein A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing,2006,54(11):4311-4322.
[18] Mairal J,Bach F,Ponce J,et al. Online dictionary learning for sparse coding [C]// International Conference on Machine Learning. Montreal,Canada:ACM,2009:689-696.
[19] Zhang Y,Yang J,Wotao Y. YALL1:Your Algorithms for l1,MATLAB Software[EB/OL]. http://yall1. blogs. rice. edu/,2010-07-15.
[20] Levin A,Weiss Y,Durand F,et al. Understanding and evaluating blind deconvolution algorithms [C]//IEEE International Conference on Computer Vision and Pattern Recognition. Miami,USA,2009:1964-1971.
[21] Levin A,Weiss Y,Durand F,et al. Efficient marginal likelihood optimization in blind deconvolution [C]// IEEE Conference on Computer Vision and Pattern Recognition. Providence,USA,2011:2657-2664.
[22] Babacan S D,Molina R,Do M N,et al. Bayesian blind deconvolution with general sparse image priors[C]// Computer Vision-ECCV 2012. Berlin,Germany,2012,7577:341-355.
(责任编辑:赵艳静)
A Union of New Patch-Dictionary Sparse Representation and Gradient Prior for Blind Image Deblurring
Yang Aiping,Liang Bin,He Yuqing,Zhang Liyun,Wei Baoqiang
(School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China)
In the light of the heavy computational loads and the limited ability in detail preserving of sparse representation-based blind image deblurring algorithms,a new method based on patch-dictionary approach and gradient prior was proposed in this paper.First,in order to increase the computational efficiency,a multimode non-overlapping strategy,in which the image recovery was independently carried out in each mode,was presented,and then the results of the subproblems were averaged to eliminate artificial effects;In addition,using thenorm as the sparsity measure,we incorporated the gradient prior into the sparse deblurring model.Finally,we designed a novel combined new patch-dictionary sparse representation and gradient prior image deblurring model in which the deblur kernel updating and the deblurred image estimating were performed in turn via the iteration.Experimental results show that the approach proposed achieves better results in both subjective and objective evaluation criteria and significantly reduces the overall complexity of the algorithm.
blind deblurring;new patch-dictionary sparse representation;sparse gradient prior
TP391
A
0493-2137(2016)09-0984-08
10.11784/tdxbz201501058
2015-01-21;
2015-05-22.
国家自然科学基金资助项目(61372145,61472274,61201371).
杨爱萍(1977— ),女,博士,副教授.
杨爱萍,yangaiping@tju.edu.cn.
网络出版时间:2015-05-28. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20150528.0828.001.html.

