REVO测头在非正交式三坐标测量机中的探测矢量修正算法
刘书桂,张海涛,苏智琨
(天津大学精密测试技术及仪器国家重点实验室,天津 300072)
REVO测头在非正交式三坐标测量机中的探测矢量修正算法
刘书桂,张海涛,苏智琨
(天津大学精密测试技术及仪器国家重点实验室,天津 300072)
REVO测头是基于正交式三坐标测量机设计和应用的,针对在非正交悬臂式整体叶盘原位测量机下应用REVO测头探测姿态不正确的问题,根据悬臂式测量机的结构特点,提出了一种探测矢量修正算法,通过将控制器返回的数据进行分离,并经过建立的旋转臂与测头之间的准刚体模型变换,得到REVO测头探测矢量与机器坐标系下被测工件表面法矢的关系,达到探测矢量修正的目的.实验结果表明:探测矢量经过修正后,测量30,mm长的量块,平均误差值从0.015,6,mm降低到0.003,7,mm,提高了测量机的测量精度,为REVO测头在非正交式三坐标测量机中的应用和深入研究奠定了坚实的基础.
整体叶盘;非正交式三坐标测量机;REVO测头;探测矢量修正
由于在重量、效率和维修等方面的优势,整体叶盘已经取代传统的叶盘,成为国外先进战斗机发动机普遍采用的结构形式[1].整体叶盘的加工质量决定着战斗机发动机的性能,因此必须对其加工精度进行检测.目前,通用的检测方法是整体叶盘加工完成后在三坐标测量机上对其加工质量进行检测,但是,检测出任何一个地方不合格,整个整体叶盘就会报废.整体叶盘的造价昂贵,如果加工好的整体叶盘成品质量不合格,就会造成巨大的人力、物力浪费以及财产的巨大损失,因此,整体叶盘的在线原位测量成为亟待解决的问题.
受加工现场条件的限制以及整体叶盘复杂结构的约束,设计了一种基于REVO测头的发动机整体叶盘悬臂式原位测量机[2-3].本文中所设计的为非正交悬臂式坐标测量机,有一个绕竖直方向做旋转运动的旋转轴,其3个主轴是非正交的,不符合REVO测头的正常应用要求.如果直接使用机器坐标系下工件被测表面的法矢作为探测矢量,REVO测头几乎不会以垂直工件被测表面的姿态进行探测,轻则会降低测量精度,重则根本不会探测到被测表面,使后续测量、测头半径补偿[4]以及自动路径规划等工作都不能正常进行.因此,必须建立修正模型[5-8],对REVO测头的探测矢量进行修正.
据此,提出了一种悬臂式测量机下REVO测头探测矢量的修正算法,根据坐标测量机的结构特点,建立旋转臂与REVO测头之间的准刚体模型,通过分离控制器返回的数据,反求出旋转臂的角度值,经过模型变换,得到悬臂式测量机下REVO测头以垂直工件被测表面的姿态进行探测的探测矢量,达到修正的目的.
1 悬臂式坐标测量机结构
图1为悬臂式测量机结构示意,图2为REVO测头系统实体.

图1 悬臂式测量机结构示意Fig.1 Sketch of the CCMM structure
如图1所示,悬臂式测量机主轴由沿水平方向运动的直行轴X、沿竖直方向运动的直行轴Z以及旋转轴R组成,定义机器坐标系X轴的正向为测量机水平向前(图1中向右)的运动方向,Z轴的正向为测量机竖直向上的运动方向,Y轴正向由右手定则确定,旋转臂的零度定义为旋转臂与X轴方向平行且指向X轴正向的位置.其中,X向和Z向运动采用直线光栅计数,其输出值的单位为毫米,Y向采用圆光栅计数,其输出值的单位为度.
REVO测头是Renishaw公司生产的可以绕水平轴A和竖直轴B做无极转动的动态测头及测座系统,如图2所示.
2 REVO测头探测矢量分析
2.1正交CMM下REVO探测矢量分析
REVO测头自身可以看作是一个小型的三坐标测量机,安装时要求REVO测头B轴的零度朝向三坐标测量机Y轴的负方向.被正确安装后,REVO测头内部坐标系的3个轴就与正交CMM坐标系的3个轴同向且分别平行.因此,REVO测头探测位于正交CMM机器坐标系下的工件表面,其探测工件表面返回的探测矢量与工件被测表面的法矢量一致.
2.2CCMM下REVO探测矢量分析
在悬臂式测量机下,旋转臂位于零度位置时,REVO测头B轴的零度朝向CCMM机器坐标系Y轴的负方向,其内部坐标系的3个轴与CCMM机器坐标系的3个轴分别平行.此时使用B轴探测返回的探测矢量与工件被测表面的法矢一致.当旋转臂绕旋转轴转过一定角度时,REVO测头内部坐标系的3个轴与CCMM机器坐标系的3个轴不再平行,垂直于工件表面探测返回的探测矢量与工件表面的法矢量有很大的不同.
如图3所示,REVO测头的B轴角度为90°,旋转臂的角度为θ,被测工件绕机器坐标系的Y轴转过相应的角度,使REVO测头以垂直被测面的姿态进行探测,其返回的理论探测矢量应为(0,1,0),而在图3机器坐标系下,工件被测表面的法矢量为(-sinθ,cosθ,0),探测矢量与工件被测面法矢量不一致.在实际的测量实践中,如果按照上述工件被测表面的法矢量进行测量,就会产生测量误差.

图3 CCMM下REVO探测矢量分析Fig.3 Analysis of detecting vector on CCMM
3 探测矢量修正算法
3.1旋转臂角度的反求
控制器返回的坐标值为(XUCC,YUCC,ZUCC),单位mm,其构成如下所示:

式中:XREVO、YREVO、ZREVO为REVO测头A轴、B轴运动在X、Y、Z方向产生的线性量;XScale、ZScale为直线光栅的输出值,mm.R轴为旋转轴,采用圆光栅计数,其输出YScale为角度值,通过对控制器返回的YUCC值(单位mm)的分解,即可得到旋转臂转动的角度值,从而进行探测矢量的修正.
建立如图4所示的REVO测头坐标系,坐标系的原点O为REVO测头的中心(A轴与B轴的交点),其中,A轴垂直纸面,B轴在竖直方向,以A轴为坐标系X轴方向,X正向与机器坐标系相同,以B轴为坐标系的Z轴方向,竖直向上为正,测头坐标系Y轴正向由右手定则确定.

图4 REVO测头自身坐标系Fig.4 Coordinate of REVO itself
令测杆的长度为L,当A轴、B轴都处于零位时,如图4(a)所示,测端P在测头坐标系下的坐标值为(0,0,-L).当测杆绕A轴转动α角时,如图4(b)所示,测端在测头坐标系下的坐标值为
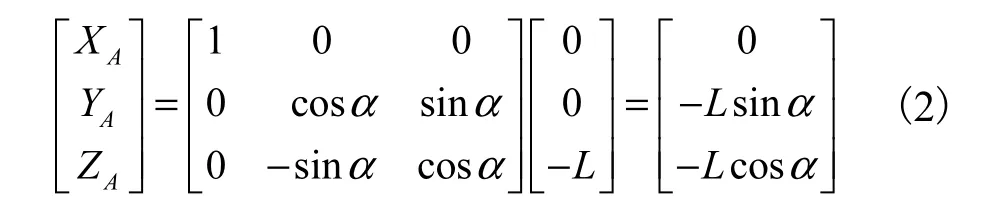
当测杆绕B轴转动β角时,如图4(c)所示,测端在测头坐标系下的坐标值为

根据式(1)与式(4),即可求出测量机3个主轴的光栅值,即

3.2探测矢量修正
如图5所示,设被测工件被测面在机器坐标系下的法矢量为(I,J,K),旋转臂绕旋转轴零位转过的角度为θ,即圆光栅的输出值YScale,(i,j,k)是在机器坐标系下REVO测头以垂直被测面的姿态进行探测的探测矢量,根据准刚体模型,可以建立两者之间的关系,即

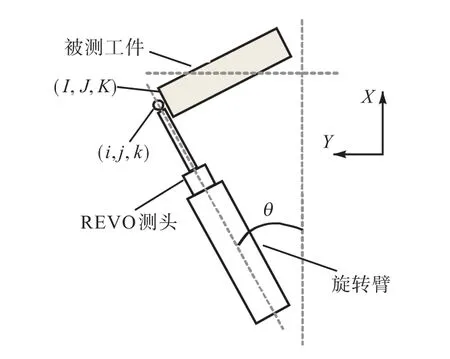
图5 探测矢量修正模型Fig.5 Correction model of detecting vector
通过式(5)与式(6),即可对机器坐标系中被测面的探测矢量进行修正,使REVO测头在探测时能够以垂直于被测面的姿态进行正确地探测.
4 仿真验证与实验数据及结果
令REVO测头A轴位于90°,B轴位于90°位置,设旋转臂绕旋转轴零位转过角度θ,被测工件绕机器坐标系的Y轴转过相同的角度θ,可以得到机器坐标系中被测工件被测面的法矢量,通过修正模型即可求出REVO测头以正确姿态探测的探测矢量,在REVO测头A轴90°、B轴90°位置,测头在探测被测工件朝向Y正向的表面时,其探测矢量为(0,1,0),在探测被测工件朝向Y负向的表面时,其探测矢量为(0,-1,0).
从表1可以看出,只要正确地给定了工件被测表面的法矢量(I,J,K),经过修正模型修正后的探测矢量(i,j,k)与REVO测头以垂直工件被测表面进行探测的探测矢量完全一致,验证了所提出的探测矢量修正模型的正确性.表2 是手动控制REVO测头尽量以垂直被测面的探测姿态探测00级平板平面后(平面法矢量为(-1,0,0))控制器返回的数据.表3中的θ 是由式(5)根据表2中的探测数据求出的旋转臂的角度值.表3的结果显示了探测矢量修正的必要性:被测平面的法矢量为(-1,0,0),旋转臂在不同的角度,REVO测头以垂直被测平面的姿态探测平面返回的探测矢量都与被测平面法矢量不同,旋转臂的角度越大,两者的相差就越大,如果以被测平面的法矢量作为探测矢量进行探测,必然会产生较大的误差.

表1 修正模型仿真验证Tab.1 Simulation of the correction model

表2 实际测量数据Tab.2 Measurement data

表3 修正后的探测矢量与实际探测矢量对比Tab.3 Comparison of the detecting vector between the correctional and the actual
在相同的条件下,分别使用机器坐标系下量块被测表面法矢量与经过模型修正后的探测矢量测量30,mm量块,测量数据与计算结果如表4所示.可以看出,使用机器坐标系下量块被测面的法矢量进行探测,3次测量的平均值与量块长度真实值之差为0.015,6,mm,使用修正后的探测矢量进行探测,3次测量的平均值与量块长度真实值之差为0.003,7 mm,在相同的实验条件下,使用修正后的探测矢量进行探测的测量误差平均值比没有修正探测矢量的测量误差平均值降低了0.011,9,mm,验证了本文所提出的探测矢量修正算法的正确性,提高了测量精度.

表4 测量30 mm量块实验数据及结果Tab.4 Data and results of measuring the block of 30,mm
5 结 语
本文提出了一种REVO测头在非正交式三坐标测量机中探测矢量修正算法,深入分析了在正交式三坐标测量机和非正交悬臂式三坐标测量机下,REVO测头以垂直工件被测表面姿态进行探测的探测矢量的不同,建立了REVO测头自身坐标系以及控制器返回数据构成的数学模型,根据控制器的返回数据反求出旋转臂的角度值,并建立了REVO测头探测矢量与机器坐标系下被测工件表面法矢的探测矢量修正模型,经过仿真与实际测量实验验证了探测矢量修正模型的有效性,极大地减小了测量误差,使后续的测量、测头半径补偿及路径自动规划都能够正常进行,对REVO测头在非正交三坐标测量机上的应用和深入研究具有重要意义.
[1] Yang Yanhui,Liu Dong,Luo Zijian. Microstructure homogeneity evaluation for TC11 blisk forging using loss function based on Taguchi method[J]. Rare Metal Materials and Engineering,2011,40(4):565-570.
[2] 裘祖荣,苏智琨,张国雄,等. 整体叶盘测量机参数标定的关键技术[J]. 纳米技术与精密工程,2014,12(4):235-241. Qiu Zurong,Su Zhikun,Zhang Guoxiong,et al. Key technology for calibrating parameters of a bladed disk measuring machine[J]. Nanotechnology and Precision Engineering,2014,12(4):235-241(in Chinese).
[3] 赵 磊,刘书桂. Revo测头的自适应测量算法及位置反解[J]. 天津大学学报,2012,45(5):430-434. Zhao Lei,Liu Shugui. Adaptive measurement algorithm of Revo probe and inverse position[J]. Journal of Tianjin University,2012,45(5):430-434(in Chinese).
[4] 张国雄. 三坐标测量机[M]. 天津:天津大学出版社,1999. Zhang Guoxiong. Coordinate Measuring Machine[M]. Tianjin:Tianjin University Press,1999(in Chinese).
[5] Li Xinghua,Zhang Guoxiong,Liu Shugui,et al. A study on machine calibration techniques[J]. CIRP Annals-Manufacturing Technology,2013,62(1):499-502.
[6] Giniotis V,Grattan K T V,Rybokas M,et al. Uncertainty and indeterminacy of measurement data[J]. Measurement,2004,36(2):195-202.
[7] Li Xinghua,Chen Bo,Qiu Zurong. The calibration and error compensation techniques for an articulated arm CMM with two parallel rotational axes[J]. Measurement,2013,46(1):603-609.
[8] 王学影,刘书桂,王 斌,等. 关节臂式柔性三坐标测量系统的数学模型及误差分析[J]. 纳米技术与精密工程,2005,3(4):262-267. Wang Xueying,Liu Shugui,Wang Bin,et al. Mathematical model and error analysis of the articulated arm flexible CMM[J]. Nanotechnology and Precision Engineering,2005,3(4):262-267(in Chinese).
(责任编辑:赵艳静)
Correction of Detecting Vector of REVO Applied in Non-Orthogonal Coordinate Measuring Machine
Liu Shugui,Zhang Haitao,Su Zhikun
(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)
REVO is designed and applied based on the orthogonal coordinate measuring machine(CMM).A correction algorithm of detecting vector of REVO was proposed according to the application of REVO to the non-orthogonal cantilever CMM(CCMM) for the blisk in-situ measurement.On the basis of separation of the data returned by the controller,the relationship between the detecting vector of REVO and the normal vector of the measured surface of workpiece was obtained via the translation of the pseudo-rigid model between rotary arm and REVO,and the correction of the detecting vector was then achieved.Experiments were carried out on measuring the block of 30,mm,and the measurement precision was improved a lot as the average error decreased from 0.015,6,mm to 0.003,7,mm.The research lays a solid foundation for the application and further research of REVO on the non-orthogonal CMM.
blisk;non-orthogonal CMM;REVO;detecting vector correction
TK721
A
0493-2137(2016)09-0956-05
10.11784/tdxbz201504085
2015-04-28;
2015-06-02.
中航工业创新基金资助项目(2009B41030).
刘书桂(1954— ),男,教授,sgliu@tju.edu.cn.
张海涛,zhanghaitao@tju.edu.cn.
网络出版时间:2015-06-26. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20150626.1642.002.html.

