孔板后台阶流动与钝化诊断中测压位置寻优
李红文,袁 超,张 涛
(天津大学电气与自动化工程学院,天津 300072)
孔板后台阶流动与钝化诊断中测压位置寻优
李红文,袁 超,张 涛
(天津大学电气与自动化工程学院,天津 300072)
针对孔板下游流场的后台阶流动问题进行了仿真研究,可知当雷诺数大于10,000后,其旋涡回流区长度固定,并且由仿真实验可以得到回流区长度数据.对于因孔板迎流面直角边磨损钝化造成的畸变流场,可用差压比值算法进行流场畸变量即钝化量诊断与测量值校正,但测压点位置寻优的实验方法采用凑试法,效率低、不具有通用性,故将旋涡稳定性用于测压点位置寻优研究中,得到了诊断算法测压点优化经验数据,实验证明其提高了寻优效率并具有通用性,同时也适用于其他类似情况.
孔板;后台阶流动;回流区;孔板磨损钝化;差压比值因子;畸变流场
后台阶流动是流体力学工程领域的典型实例,它包含了流动分离、再附、旋涡运动等三维复杂流动的特征,在复杂流动及湍流研究中占有重要地位,在工程实践中具有广泛的应用.而标准孔板节流器件下游流场类似于环形后台阶流场,其流动特点与后台阶流场具有相似的特点.针对后台阶流动,Spazzini等[1]、Barkley等[2]进行了实流实验研究,肖潇等[3]进行了计算流体动力学(CFD)研究并结合粒子图像测速技术(PIV)实验数据进行验证,这些研究都证明后台阶的旋涡稳定性与雷诺数有关.而艾万政等[4]对水利工程中消能孔板的下游流场的研究,证明当雷诺数足够大时,孔板后台阶流动稳定,并得出回流区长度经验公式.
本文在上述研究成果基础上,借助CFD仿真证明,对于流量测量的节流孔板,其下游流场的旋涡具有稳定性.其回流区长度与雷诺数符合一定规律.
应用标准孔板时,应符合国家标准规定.但实际中往往出现偏离国家标准的工况,造成流出系数值偏离标准中的规定值,而偏离情况在管道内不可见,这使得测量结果偏离准确值,例如最常见的典型工况是孔板入口直角边缘磨损钝化,孔板上游异物淤积,孔板迎流面沉积或沾污污物,孔板及管道粗糙度变大等等.文献[5-6]针对这些非正常工况,提出了畸变流场差压比值诊断法,用于诊断孔板的非正常工况程度与校正测量值.根据非正常工况所导致的流场畸变,在孔板下游增设一诊断测压点P3,与孔板测流量的两个测压点(P1与P2)进行差压比值运算.通过差压比值情况,来推知流场的畸变程度,从而推知非正常工况的量值,校正测量值.在研究中,诊断测压点P3的位置选择合适与否对诊断与校正效果具有明显影响,文献[5-6]中采用实验与仿真相结合的凑试法来优化P3点所在的合适位置.但效率不高,对不同规格的孔板要重新凑试,没有通用性.所以本文结合孔板下游回流区的相关研究,针对不同规格尺寸的孔板,得出其诊断测压点P3的最优位置区间,列出相应经验数据,并通过实验验证.
1 标准孔板下游旋涡与CFD仿真
1.1标准孔板下游旋涡描述
图1与图2为孔板结构与孔板后台阶旋涡示意.当流体流过孔板时,在孔板迎流面爬升,在背流面,流体从孔口喷射出,在孔板边缘分离,在下游管道中形成受限射流.

图1 孔板结构示意Fig.1 Orifice plate structure diagram
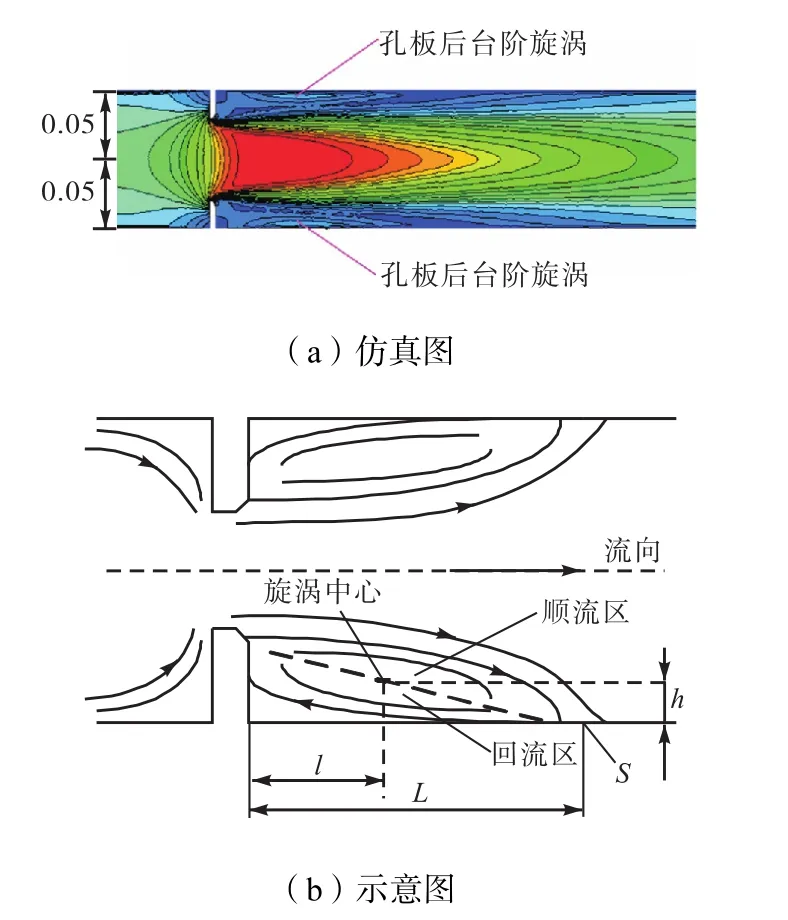
图2 孔板后台阶旋涡示意(单位:m)Fig.2Sketch diagram of backward-facing step vortex of orifice plate(unit: m)
孔板下游流场属于后台阶流动,同时也属于受限射流的湍流状态(Re>5,000).湍流是一种参数随时间和空间作随机变化的不规则的流动状态,但它并不是完全不规则的随机运动,在表面看起来不规则的运动中隐藏着某些可检测的有序运动,称为拟序运动.这种运动的结构,是指在切变湍流场中不规则触发的一种有序运动,它的起始位置和时刻是不确定的,但一经触发,它就以某种确定的次序发展为特定的运动状态.研究者对受限射流拟序结构进行了研究,认为孔板下游流场是一种大涡拟序结构[7-8].当雷诺数变化,例如流体速度增加,孔板下游旋涡的强度随着流体速度的增大而增强,而旋涡的形状具有一定规律,与以下几个因素有关:管道直径D,孔板孔径比β,孔板厚度E.
文献[4,8]中认为,孔板大涡拟序结构,流体产生卷吸与合并现象,射流由于受到管壁的限制,分离剪切层向下游并向靠近管壁的方向扩散,最终抵达管壁而附着在管壁上,在附着点S向右,形成湍流边界层,在点S向左,形成回流区,这样孔板下游就形成了旋涡,旋涡是三维轴对称形式的涡环结构,点S的轨迹为沿着内管壁一周.孔板下游回流区距离孔板下游端面长度为L,即点S距离孔板后端面的距离.旋涡中心距离孔板后端面距离为l,距离管壁高度为h.旋涡中心的轨迹为垂直于轴向直线的圆形.回流区长度L值是本文研究内容的关键.下面通过CFD加以说明.
1.2孔板管道系统的CFD概述
本文中采用的Fluent是流体力学研究所用的CFD软件中最为典型的一种.孔板尺寸规格如图1所示.管道内径D=100,mm、孔板的孔径比β=0.75及0.60;D=50,mm、β=0.75及0.50;孔板厚度E为2,mm;节流孔厚度e为1,mm.孔板的前后直管段长度分别为50D与30D,流体介质为标况下的水.
进行CFD仿真研究,首先需要证明孔板后旋涡的时间稳定性与空间稳定性,即L、l、h这3个量值的大小与变化,以此为基础进行后续寻优研究.
模型的网格划分方法见文献[5-6],要点为:GAMBIT网格划分需要做到疏密得当,这通过尺寸函数来实现,同时采用Fluent软件中的网格自适应功能,这里不再详述.
Fluent仿真控制方程采用标准k-ε黏性模型,采用三维单精度求解器,残差设为0.000,1,离散格式为一阶迎风格式,管道入口为速度入口,出口为自由流出口.
1.3孔板后旋涡的时间稳定性验证
CFD中所采用k-ε黏性模型属于定常模型或稳态模型,应用这一模型的前提是在假设一定雷诺数下,孔板下游是稳态的流场,为力求严谨,这点首先需要验证.
利用Fluent的非稳态模型对孔板流场进行验证,网格划分与稳态仿真相同.取D=100,mm、β=0.60的孔板,在恒定的入口速度,即雷诺数Re为1.0×106工况下,取孔板上游0.9D、0.6D、0.3D处,孔板下游0.3D、0.6D、0.9D、…、3.0D处,以及孔板前后端面共15个点的静压值,计算模型中取时间步长为0.005,s,仿真总时间为10,s.
孔板前后流场压力值随时间变化情况如图3所示.图中横轴代表管道中的位置,0点左侧表示孔板迎流面即上游端面,0点右侧表示孔板背流面即下游端面,这两点间距离为孔板的厚度E.由于孔板的阻碍作用,在孔板上下游端面间,产生了能量损失,造成压力值突变.
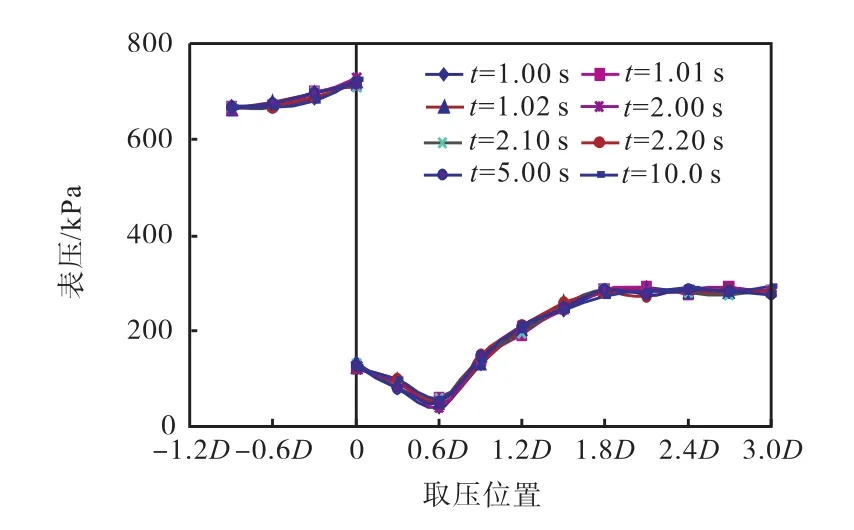
图3 孔板后台阶流动的时间稳定性仿真Fig.3 Time stability simulation of backward-facing step flow of orifice plate
图3中所列的时间间隔,包括0.01,s、0.10,s、1.0,s、5.0,s,从图3中可知,如雷诺数固定,孔板前后的静压值不随时间变化,于是孔板下游流场是稳定的,从而旋涡具有时间稳定性.当选取其他雷诺数以及不同的规格参数的孔板进行仿真计算时,除了具体表压值不同外,曲线都与图3类似,各条曲线重合,变化趋势相同.
1.4孔板后旋涡的空间稳定性
1.4.1孔板后旋涡形态的影响因素与仿真
孔板后台阶旋涡的形状,通过L、l、h 3个量来描述.仿真研究的目的,是研究旋涡的形状与Re、D、β、E等因素的关系.具体步骤为2步:①针对具体尺寸的孔板,研究回流区长度L与Re的关系;②确定在相同Re下,旋涡形状随D、β、E等的变化规律.
旋涡回流区长度确定方法为:经过管道中心的纵向剖面,在速度矢量图中找到回流点所在管壁上的位置所处的区域,在此区域内,有一反向回流的速度为0的点,在该点右侧,存在主流区再次附着管壁的情况,该点(即点S)到孔板背流面的距离即为回流区长度L.
孔板下游旋涡中心按如下方法确定:取经过管道中心的纵向剖面,在速度矢量图中寻找旋涡中心的位置范围,在这个范围内,通过仿真数据寻找速度矢量趋近于0的点,而旋涡强度在这一点经计算也趋近于零,或为无穷小量,这一点就是旋涡中心的准确值.
旋涡的空间稳定性是指描述孔板下游旋涡的回流区长度以及旋涡中心位置,随入口速度变化具有一定的规律.
1.4.2孔板后旋涡的数学描述
根据标准孔板CFD计算,按步骤①,得到孔板下游旋涡数据如表1所示.

表1 孔板后旋涡仿真计算L值(不同Re)Tab.1CFD L value of vortex behind orifice plate (different Re)
表1中,当雷诺数逐渐增大并超过10,000后,孔板后回流区的长度L趋于固定值,同时每只孔板的旋涡中心位置也处于固定位置.
按步骤②,在雷诺数5.0×104的情况下,D=100,mm,孔板厚度E为2~10,mm的孔板(节流孔厚度为1~9,mm),β取0.3、0.4、…、0.8的情况下,回流区L的情况如表2所示.

表2 孔板后旋涡仿真计算L值(不同β)Tab.2 CFD L value of vortex behind orifice plate (different β)
取D=50,mm、80,mm的孔板,研究回流区长度,其回流区长度与表2的差距在±0.003D之内,可见,表中数据具有通用性.
回流区长度有如下特性:在雷诺数与管道直径D一定时回流区长度随着β的增加而显著地减小;孔板厚度增加时,回流区长度减小,但减小的程度很小.
2 孔板非正常工况下旋涡稳定性研究
标准节流装置应按国标GB/T,2624—2006[9]来设计制造安装和使用,此时差压信号及其测量误差才符合标准的规定.但在现场应用中经常发生偏离标准的非正常工况,孔板迎流面直角边磨损钝化,是一种典型非正常工况.本节以这一典型实例,研究其下游旋涡稳定性.
2.1典型的钝化工况描述
标准孔板因磨损等原因钝化后锐利度下降,其流出系数发生偏差,文献[10]已给出校正公式,如图4所示.

图4 钝化后孔板示意Fig.4 Blunt orifice plate diagram
根据国家标准[10]的规定,孔板入口边缘圆弧半径rk应不大于0.000,4,d(此时视为标准孔板钝化量为0),这是一个很严格的要求,而超出了这个要求,孔板如果要继续使用,就要对流出系数进行校正,计算公式为


式中:C1为校正后的流出系数;C为根据国家标准计算出的标准流出系数;bk为孔板入口边缘锐利度校正系数.bk与钝化程度B(B=rk/d)具有明确的对应关系,如表3所示.
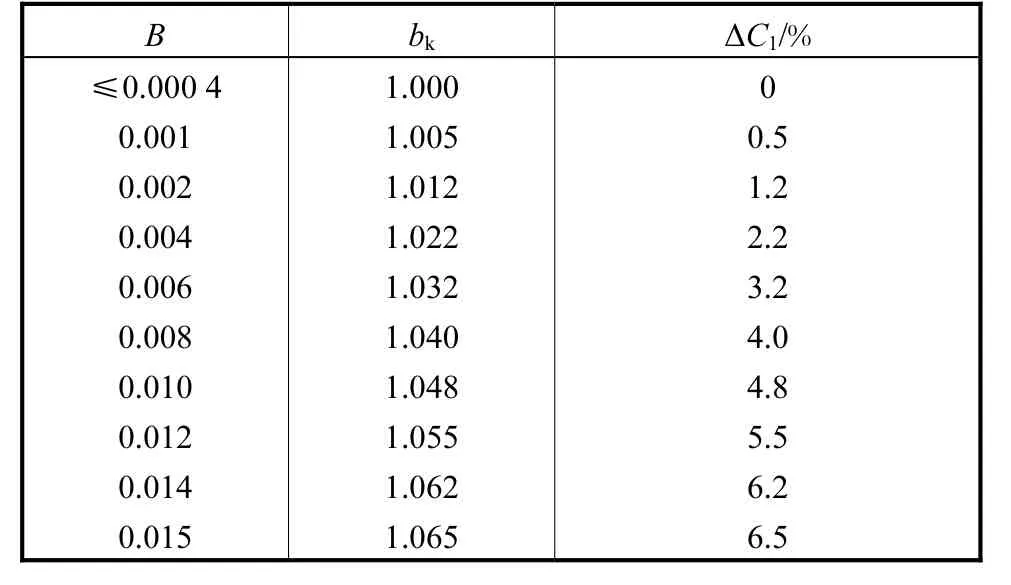
表3 钝化程度与校正系数bkTab.3 Bluntness and correction coefficient bk
rk的大小,即直角边被磨损后产生的圆弧的半径,表示了钝化量,ΔC1为钝化后流出系数偏离国家标准的百分量,显然,只要孔板规格确定,rk与B成正比.表3的优点在于,不论管道直径D、孔板的β值多大,校正系数只与钝化产生的圆弧半径rk及节流孔直径d二者比值有关.可见,只要准确地知道B,则可以很方便地校正流出系数,从而得到准确的流量值.
2.2钝化孔板下游的旋涡稳定性研究
用标准孔板类似的研究方法可得,孔板钝化后具有时间稳定性,不再详述.采用同样方法,研究发现钝化孔板后旋涡具有空间稳定性.
孔板尺寸确定后,其入口直角边磨损钝化的程度不同,其旋涡中心位置、回流区长度,均有所变化.具体如表4所示,研究中孔板参数为D=100,mm、β=0.6、E=2,mm、e=1,mm,Re为5×104.
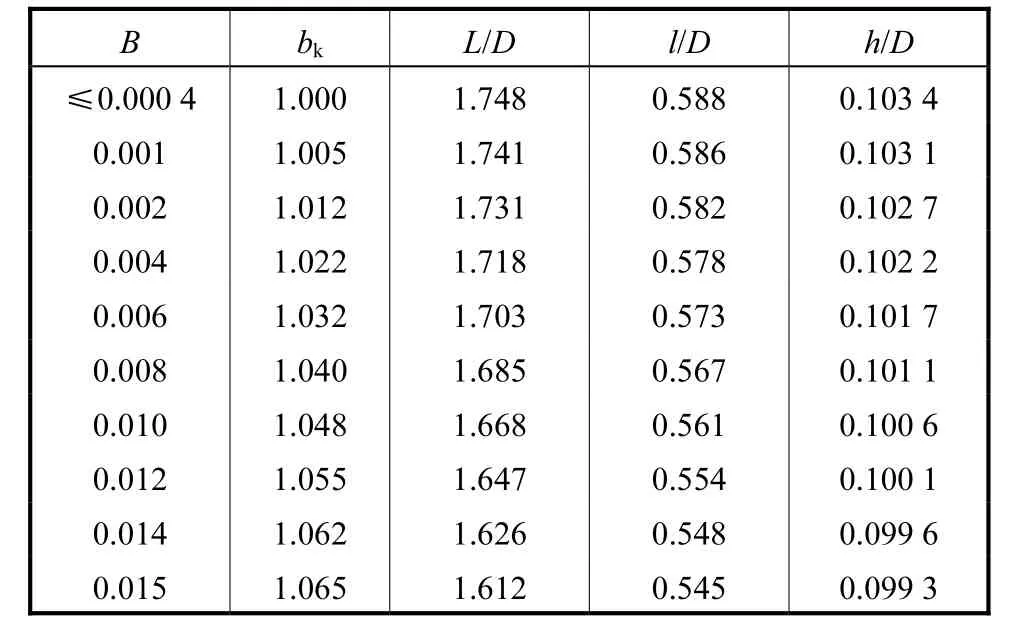
表4 钝化孔板后旋涡仿真Tab.4 CFD simulation of vortex after blunt orifice plate
可见,孔板结构确定后,钝化量越大,流体流经孔板的压力损失就更少一些,其回流区长度越小.此时,在不同钝化程度下,回流点S位于一个区间内,即S位于[1.612,D,1.748,D]内.钝化程度B增大,旋涡中心位置也更靠近孔板下游直角区方向(l与h减小),但程度很小.当雷诺数大于10,000以上,只要B确定,回流区长度以及旋涡中心位置不变.
2.3其他非正常工况下旋涡的稳定性
仿真研究中,对以下工况进行了探讨:模拟天然气或煤气测量孔板,上游水分凝结沉积,污物淤积[11],孔板迎流面沾污固体物质(如奶液)流量测量中,奶油沾污孔板迎流面[12],天然气测量中含硫的析出物沾污管壁与孔板迎流面,等.发现在各种非正常工况下,孔板下游的旋涡同样具有稳定性,当雷诺数在10,000以上,其回流区长度为固定值,不随流体速度变化.采用上文类似的研究方法,可以得出时间稳定性与空间稳定性的结论.因为迎流面直角边磨损钝化更常见,具有典型性,故作为研究重点.
3 基于旋涡稳定性的诊断测压点寻优
3.1钝化畸变流场诊断法描述
流量稳定前提下,质量流量一定,则孔板上游入口速度一定,因孔板磨损钝化,与无钝化工况比较,流场发生畸变,表现为流体流经孔板压力损失减小.根据伯努利方程可知,孔板下游的静压梯度就会比正常工况下小,钝化程度越大,流场畸变程度越大,静压梯度改变越明显.诊断算法原理是用静压的改变程度来推算流场畸变程度,即钝化程度.
在测量中流量未知,仅通过法兰测压或者径距测压(测压点设为P1与P2),无法推测钝化程度,于是在孔板下游增设诊断测压点(P3),通过差压比值的不同反映静压梯度的变化程度,来反映磨损钝化后静压的变化,从而反映钝化程度,进而校正测量值.算法为计算比值

式中:η为差压比值因子;p1、p2与p3分别为P1、P2与P3点的静压值(表压);实验与仿真中发现,钝化程度越大,η值越偏离标准孔板(无钝化).文献[5-6]已对差压比值因子进行了有效的应用.
对于结构尺寸确定的标准或钝化孔板,从孔板下游速度或静压云图数据中可知,其流场具有相似性,当Re大于10,000时,速度场或静压场梯度是相同的,并且孔板下游旋涡回流区长度已确定,所以差压比值因子η与流体的流速无关,接近一个恒定值.这样可知P3点,可任意选取,只要与P2点不重合即可,但是研究中发现,η的数值与P3点的位置有关,针对不同规格尺寸的孔板,只有选取P3最优的位置区间,η恒值特性才更显著,才能对钝化程度准确诊断.
3.2P3最优位置区间的确定方法
如何选择诊断测压点P3的最优位置,通过一个CFD仿真及实流实验的实例引入.
图5是D=100,mm、E=2,mm、e=1,mm、β=0.60的孔板在不同钝化程度下,差压比值因子曲线,其中P3点选取孔板下游2.1D处.

图5 不同速度和B值下的η变化曲线Fig.5 Curve of η under different flow rates and B
从图5中可见,当流体速度在[1,6],m/s范围内,取不同的钝化程度下的η值,曲线比较平直,接近于一条直线.计算不同钝化程度下的6个速度点的差压比值因子的方差,进行比较,结果绘制于图6中.

图6 P3=2.1D时不同B值下η的方差Fig.6Variance of η under different values of B when P3=2.1D
显然,η的方差越小,说明该钝化程度下图5中的曲线越平直,η越接近恒定值,此时速度变化对η所造成的影响就越小,对钝化的诊断就越准确.
而选择P3位于其他不同位置,取孔板下游0.4,D至2.4,D,间隔0.2,D,计算各个钝化程度下差压比值因子的方差,所得到的曲线,绘制在同一幅图中进行比较研究,如图7所示,文中方差量级为10-3.
从图7中可见,位于下方的4条曲线的方差值在[5.0,6.0]之间,代表的η的方差比较小,说明作为P3的测压点位置适宜.它的位置分别为1.0,D、1.2,D、2.0,D、2.2,D.而位于上方的2条曲线方差在[8.0,9.5],代表P3取1.6,D与1.8,D,此时η的方差较大,最不适宜作为P3的位置.而图6中2.1,D是采用凑试法得到的P3点的位置,此时的方差,与图7中最低端的4组曲线处于同样范围内.

图7 不同B值下η的方差Fig.7 Variance of η under different values of B
3.3P3最优位置区间讨论
诊断测压点P3所在的最优位置区间如何确定,这个问题与上面研究所得到的孔板后漩涡稳定性结论有直接的关系,经分析,得到几个结论.
(1)如果P3点与旋涡回流点S点很接近,是最不适宜的.原因如下:假定流量是恒定稳态流动,这只是理想的情况,流量不可能绝对稳定,当流体从孔板孔口喷射出,形成孔板的后漩涡的过程中,在旋涡回流区长度的位置存在大涡拟序结构的振荡,这必然造成S点位置处的静压有微小的波动,压力的稳定性差,这个振荡影响P3点的静压值p3的稳定性,所以影响η的恒值性,所以P3点应明显地离开S点.
第3.2节的实例中,对于不同钝化程度的孔板,旋涡回流区长度为1.612D~1.748D,即S位于[1.612D,1.748D]内,当P3点取1.6D与1.8D正好位于S区间两侧,距离很近,这就是这两点方差最大的原因.又有1.4D距离S区间比较近,方差比较大,为[7.0,8.1].经计算,如果P3点取在1.7D处,落在S区间内,η的方差显著增大,达到11.245.
(2)如果P3点靠近下游测压点P2,这样,尽管P3点距离S点比较远,P3点压力较稳定,但是P3点距离P2如果较近,则p3与p2的差压值接近,这就容易造成式(3)的分母部分过小,则η的数值偏大,尽管对仿真计算影响不大,但对于实际仪表装置,对于流速的波动,p3-p2过小,则比值η抗干扰能力低,容易放大误差,对诊断钝化不利.实例中,0.4D、0.6D、0.8D就属于这种情形,此时η的方差在[6.0,8.0].
(3)从仿真与实验中得到如果P3点在孔板下游比较远的位置,这样P3距离S点比较远,距离P2点也比较远,似乎对于辨识钝化有利,实际上不然.
这是因不同钝化程度的孔板,钝化B对流场的压力梯度的影响,只有在孔板下游2.5,D之内,才比较明显,而在孔板下游2.5,D之后,流场开始逐渐恢复成充分发展的状态,孔板造成的压力损失也逐渐恢复,P3在下游距离孔板越远,不同钝化程度下的η数值就逐渐接近,表现为图5中的各组曲线距离变得密集,这对于钝化诊断的分辨率下降.
实例中2.4,D、2.6,D就是此种情况,此时η的方差在 [6.2,8.0],如果P3取在2.6,D之后,方差还会有继续加大的趋势.
3.4P3最优位置实流实验验证
P3位置寻优的目的是诊断畸变流场与钝化量,校正测量值,在研究过程中,仿真计算与实流实验是同时进行的.首先采用实验室内的水和空气流量标准装置,做了大量的实验工作,最后进行现场验证.识别算法后求得的bk结果误差在最大不超过±1.0%,,即识别算法的精确度为±1.0%,,此时P3点取孔板下游2.1,D处.实验中采用法兰测压套件,将P3测压点改为其他位置进行实流实验,重新进行实验,计算钝化程度,结果如表5所示.

表5 P3最优位置实流实验验证Tab.5 Real flow experiments on the optimal position of P3
从表5中可见,实流实验证实,P3最优测压点为1.1,D、2.1,D,最差的测压点为1.7,D,这与第3.3节根据CFD仿真得到的孔板后回流长度分析讨论结果相符合,从而说明仿真分析正确.
3.5不同规格孔板P3最优位置确定
为寻找测压点P3最优位置区间更普遍性的结论,采用第3.2节中的研究方法,针对各种不同尺寸的孔板,利用仿真计算数据,得出P3取不同位置时,不同钝化程度下差压比值因子的方差的平均值,当β=0.40、0.50、0.60时得到图8(a),当β=0.65、0.70、0.75时得到图8(b).

图8 不同β值下η的方差平均值Fig.8 Mean of variance of η under different values of β
在图8中,与表2或图4相互参照,每条曲线的最大值点基本都位于该β值下的回流点S区间内,再结合第3.3节中的讨论,选取因子η方差的平均值最小的区间,在回流点S的位置一侧或两侧,应距离S点至少应0.3D或以上,因为差压比值因子诊断法可适用于法兰测压与径距测压,故距离测压点P2要在0.4D以上.于是得到表6如下.除个别区间外,下面表格数据对法兰测压、径距测压都适用.

表6 P3最优位置区间(D=100,mm)Tab.6 Optimal range of P3(D=100,mm)
采用同样过程,得到D=50,mm、80,mm的P3点最优位置区间经验数据,与表5略微不同的是,仅仅是β=0.40、0.75两种情况,如表7所示.

表7 P3最优位置区间(D=50,mm,80,mm)Tab.7 Optimal range of P3(D=50,mm,80,mm)
在表6、7中,孔板厚度为4,mm,同样适用于厚度为3与5,mm的孔板,对于其他厚度的孔板,回流区长度,根据表2与表4来确定,进而可求取P3点最优位置区间,事实上因为孔板厚度对回流区数值影响很小,所以P3点最优位置区间的变化很微小.
基于孔板后旋涡稳定性的P3点寻优的讨论中,Re大于10,000时回流区长度L固定,雷诺数Re在5,000至10,000范围内,回流区长度稍小于固定值,对表6、7影响很小,结论同样适用,这样基于回流区稳定性的诊断中P3点寻优适用孔板的全部工作范围.从研究过程可知,在Re大于10,000条件下,上面的经验数据适用于其他流体介质,也适用于孔板的其他非正常工况的流场畸变诊断算法的测压点位置寻优,以及类似的节流元件.
4 结 语
本文验证了孔板下游回流区旋涡的稳定性,将雷诺数在一定范围时,其回流区长度固定这一特点,应用于差压比值法诊断磨损钝化孔板畸变流场的测压点寻优之中.仿真与实流实验证明,寻优方法有效,比之前采用的凑试法提高了功效,而且研究所得到的经验数据具有一定的通用性.
孔板迎流面直角边缘磨损钝化属于非正常工况中典型的一种,对于其他非正常工况,同样可以结合孔板下游的旋涡稳定性这一特点,通过畸变流场差压比值诊断算法测压点寻优,更准确地进行诊断及测量值校正.
[1] Spazzini P G,Luso G,Onorato M,et al. Unsteady behavior of back-facing step flow[J]. Experiment in Flu-ids,2001,30(5):551-561.
[2] Barkley D,Gabriela M,Gomes M,et al. Threedimensional instability in flow over a backward-facing step [J]. J Fluid Mesh,2002,473(1):167-190.
[3] 肖 潇,吴时强,樊新建,等. 后台阶流的水动力特征[J]. 江苏大学学报:自然科学版,2014,35(2):149-153. Xiao Xiao,Wu Shiqiang,Fan Xinjian,et al. Hydraulic characteristics of backward-facing step flow[J]. Journal of Jiangsu University:Natural Science Edition,2014,35(2):149-153(in Chinese).
[4] 艾万政,周 琦. 孔板后回流区长度数值模拟研究[J]. 水动力学研究与进展:A辑,2011,26(6):731-735. Ai Wanzheng,Zhou Qi. Study on the length of the recirculation region behind the orifice plate based on numerical simulation [J]. Chinese Journal of Hydrodynamics:Series A,2011,26(6):731-735(in Chinese).
[5] 李红文,张 涛. 钝化孔板下游流场畸变在线识别与测量值修正[J]. 农业机械学报,2014,45(6):317-323. Li Hongwen,Zhang Tao. Orifice inlet edge bluntness online identification and correction based on downstream flow field distortion [J]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(6):317-323(in Chinese).
[6] 张 涛,李红文. 孔板流量计上游淤积故障诊断与修正研究[J]. 化工自动化及仪表,2013,40(10):1232-1237. Zhang Tao,Li Hongwen. Fault diagnosis and correction of orifice meter with upstream water deposition[J]. Control and Instruments in Chemical Industry,2013,40(10):1232-1237(in Chinese).
[7] 王 池,王自和,张宝珠,等. 流量测量技术全书[M]. 北京:化学工业出版社,2012. Wang Chi,Wang Zihe,Zhang Baozhu,et al. The Flow Measurement Technology Encyclopedia [M]. Bei-Jing:Chemical Industry Press,2012(in Chinese).
[8] 王 兵,张会强,虞建丰,等. 后台阶分离流动中大涡结构演变的数值模拟[J]. 力学季刊,2003,24(2):166-172. Wang Bing,Zhang Huiqiang,Yu Jianfeng,et al. Numercial simulation of large eddy structures evolution behind backward-facing step [J]. Chinese Quarterly of Mechanics,2003,24(2):166-172(in Chinese).
[9] 中华人民共和国质量监督检验疫总局. GB/T 2624—2006 流量测量节流装置用孔板,喷嘴和文丘里管测量充满圆管的流体流量[S]. 北京:中国标准出版社,2006. General Administration of Quality Supervision,Inspection and Quavantine of the People's Republic of China. GB/T 2624—2006 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full-Part[S]. Beijing:Standards Press of China,2006(in Chinese).
[10] 中华人民共和国质量监督检验疫总局. GB/T 21446—2008用标准孔板流量计测量天然气流量[S]. 北京:中国标准出版社,2008. General Administration of Quality Supervision,Inspection and Quavantine of the People's Republic of China. GB/T 21446—2008 Measurement of Natural Gas Flow by Means of Standard Orifice Meter[S]. Beijing:Standards Press of China,2008(in Chinese).
[11] Li Hongwen,Zhang Tao,Zhang Jinjing. Malfunction diagnosis of sludge deposition in standard orifice plate flowmeter [C]//IEEE 2nd International Conference on Measurement,Information and Control. Harbin,China,2013:1319-1323.
[12] Michael R H,Neil B. The effect of contaminated orifice plate on the discharge coefficient [J]. Flow Measurement and Instrumentation,2012,25(3):2-7.
(责任编辑:王晓燕)
Backward-Facing Step Flow of Orifice Plate and Pressure Measuring Location Optimization in Bluntness Diagnosis
Li Hongwen,Yuan Chao,Zhang Tao
(School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)
In view of the backward-facing step flow of orifice plate flow field,simulation study was conducted and it was validated that the length of recirculation region could be fixed and length data could be obtained when Re is greater than 10,000.The right angle of inlet edge of orifice is often blunt because of abrading,and the bluntness can be diagnosed by differential pressure ratio factor.But experiment method has been employed to optimize the pressure points of diagnosis algorithm,which has low efficiency and lacks versatility.So vortex stability was introduced to optimization study.The experience data of pressure points optimization was gained and experimental results show the efficiency and generality of the method.At the same time,this method can also be applied to optimization diagnosis algorithm of other abnormal conditions of orifice plate.
orifice plate;backward-facing step flow;recirculation region;bluntness of orifice plate;differential pressure ratio factor;flow field distortion
TP391
A
0493-2137(2016)09-0992-08
10.11784/tdxbz201408016
2014-08-03;
2015-05-05.
国家高技术研究发展计划(863计划)资助项目(2007AA04Z180);国家自然科学基金资助项目(60974118).
李红文(1970— ),男,博士,工程师,lize739@163.com.
张 涛,zt50@tju.edu.cn.

