基于累积损伤的张力腿平台疲劳及时变可靠性评估

余建星，刘 杰，余 杨，黄福祥，樊志远，王华昆

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 高新船舶与深海开发装备协同创新中心，上海 200240；3. 海洋石油工程股份有限公司，天津 300451）

基于累积损伤的张力腿平台疲劳及时变可靠性评估

余建星1,2，刘 杰1,2，余 杨1,2，黄福祥3，樊志远1,2，王华昆1,2

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 高新船舶与深海开发装备协同创新中心，上海 200240；3. 海洋石油工程股份有限公司，天津 300451）

张力腿平台在各种恶劣海况和复杂交变载荷作用下，平台结构疲劳破坏是结构失效的重要形式.首先，基于累积损伤的疲劳寿命谱分析方法，系统地建立了平台关键部位的疲劳可靠性分析方法.然后，建立张力腿平台的整体结构模型，计算得到其在工作海况下主体结构的应力传递函数.同时引入疲劳累积损伤增加函数，提出了一种针对平台各关键部位的疲劳可靠性的时变性分析方法，得到张力腿平台的时变疲劳可靠度，并通过实例计算验证了方法的适用性和可靠性.

张力腿平台；疲劳可靠度；累积损伤；谱分析法；时变可靠度

深海蕴藏着丰富的油气资源［1］，张力腿平台（tension leg platform，TLP）凭借运动性能好、抵抗环境荷载作用能力强等优点，已成为深海油气资源开发的一种主要平台［2］.由于处在各种恶劣海况和复杂交变载荷作用下［3］，平台结构疲劳破坏是结构失效的重要方面，因此，进行张力腿平台结构的疲劳可靠性研究具有重要意义.

从目前的国内外研究情况来看，对于TLP，已有的研究主要集中在TLP张力腿系索系统的疲劳分析领域.Siddiqui等［4］采用了一次二阶矩和蒙特卡洛方法模拟计算了张力腿平台筋腱的疲劳可靠性；余建星等［5］同时采用S-N曲线方法和断裂力学方法，计算了张力腿平台系索系统的疲劳可靠性.在平台主体的疲劳可靠性领域，目前主要是针对半潜平台［6-7］，而国内外针对张力腿平台的的研究成果不多.另外，基于时变的可靠性研究方法，目前国内外主要集中在钢筋混凝土结构的安全寿命评估，而在海洋工程领域的运用几乎是一片空白［8-10］.

笔者采用基于累积损伤的疲劳寿命谱分析方法，采用水动力分析软件SESAM，求出张力腿平台在不同工作海况下的主体结构应力传递函数，系统地研究了平台关键部位的疲劳可靠性.同时，结合疲劳累积损伤增加函数，提出了一种针对各关键部位疲劳可靠性的时变性分析方法，从而得出张力腿平台的时变疲劳可靠度.

1　基于累积损伤的疲劳可靠性分析方法

1.1基于累积损伤的疲劳寿命分析方法

本文的平台结构的疲劳分析主要考虑海浪荷载的作用，运用疲劳谱分析法，分析步骤如下.

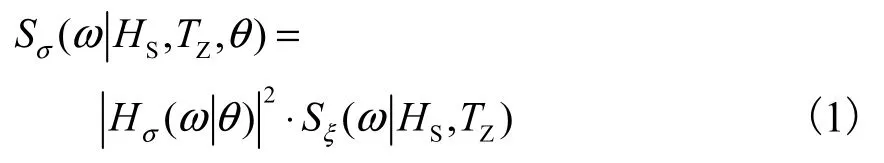
（3） 计算应力能量谱的谱矩，第n阶谱矩

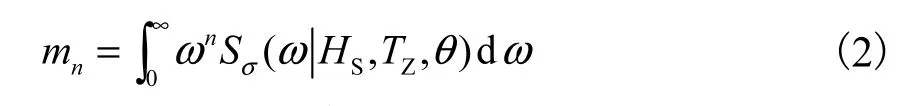
（4） 应用得到的谱矩，则应力范围短期分布的概率密度函数（雷利分布）可以表示为

式中σ为应力谱的零阶矩的平方根.

（5） 应用迈因纳准则（Miner law）计算累积疲劳损伤，对波浪散布图中各个短期海况（假设共M 个）造成的损伤Di（i=1，…，M）进行累加，即可得到总的累积损伤D，即

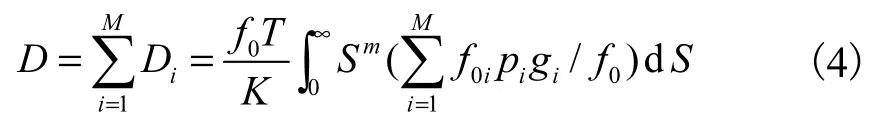
式中：f0为计算点在结构整个生命期中的应力范围S的“平均”频率，为有义波高和上过零周期的联合概率.

（6） 损伤计算解析表达式如下.

对于两段直线的S-N曲线，在拐点（NQ，SQ）处，该S-N双直线的直线段的m变为r=m+Δm（Δm＞0），常数由K1变为K2.在这种情况下，疲劳损伤为

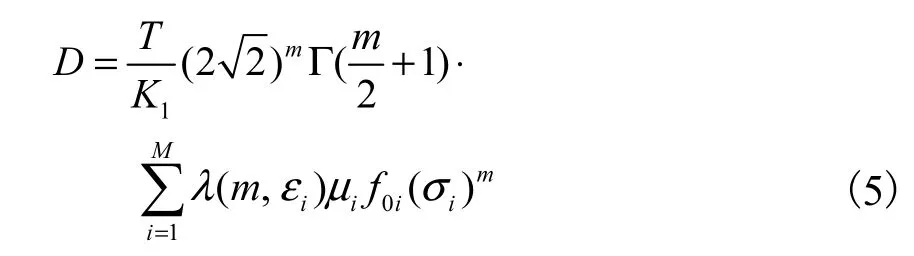
式中：Γ为伽马函数；λ为威尔逊雨流修正因子；εi为谱宽；μi为持续参数，在0和1之间.

（7） 疲劳寿命.

结合平台的设计寿命和节点的疲劳安全因子，疲劳寿命可以表示为1.2 基于累积损伤的疲劳可靠性分析方法

在疲劳寿命可靠度的计算中，常常引入应力参数Ω的概念，当应力范围的短期分布为雷利分布时，同时考虑威尔逊雨流修正因子λ和低应力范围作用下疲劳损伤修正系数Λi，应力参数［11］可表示为

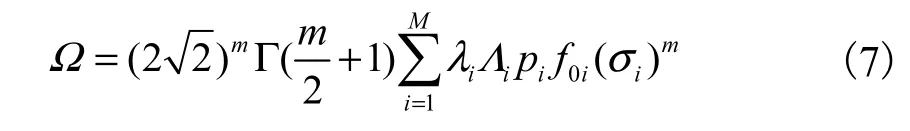
引入应力参数的概念后，结构的疲劳寿命可以表示为Tf=A/Ω.考虑计算所得的应力范围与真实的应力范围之间存在着误差，用随机变量B表示；由于Miner理论本身的近似性存在的误差用随机变量Δ来表示，结构的疲劳寿命成为

式中A、B、Δ均为随机变量.因此，结构的疲劳寿命Tf也是一个随机变量.

于是，结构的疲劳失效概率可表示为

由于A、B、Δ均为对数正态分布的随机变量，采用对数正态格式，安全裕量方程可以写成

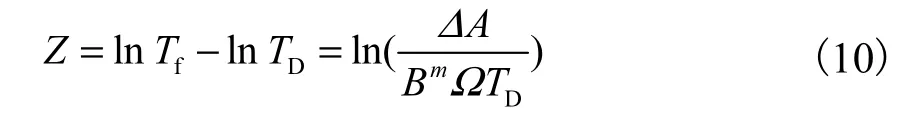
于是可靠性指标可表示为

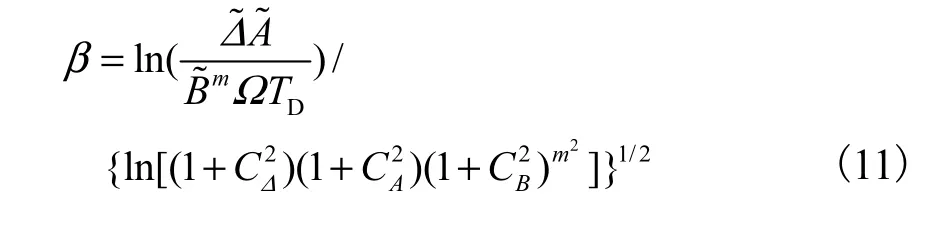
2　关键节点的应力传递函数

2.1平台信息简介

TLP浮体结构由浮箱、立柱、上部甲板及设备3部分组成，其几何参数和示意图见表1和图1.

表1　张力腿平台主要参数Tab.1 Main parameters of TLP

图1　张力腿平台的示意Fig.1 Schematic diagram of TLP

2.2平台的有限元模型和疲劳分析的关键节点

1） 平台的有限元模型

建立平台总体有限元模型时，首先根据构件的构型、外载荷的作用方式以及结构功能将构件分为3类：主要构件（对平台结构整体完整性有重要作用的构件，如立柱、浮箱外板等）、次要构件（其失效后不可能影响平台结构整体完整性的构件，如立柱、浮箱等的内部结构）和特殊构件（在关键载荷传递点和应力集中处的构件，如立柱和浮箱外板的交接部分等）［12］.然后确定模型的粗网格尺寸，根据构件的特性，对其设置不同的网格大小，并对局部进行逐步的网格细化和优化.对于主要构件，把网格都控制调整为四边形网格，只在个别结构交叉处和开孔处允许出现少量的三角形单元.这样经过反复的网格形状调整和尺寸控制，张力腿平台总体有限元模型共有64,164个节点和107,942个单元.

此外确定平台的边界条件，也是建立平台有限元模型的重要环节.对于重力与浮力不平衡的张力腿平台，相关文献和工程上一般将张力腿模拟成线性弹簧单元作为张力腿平台总体强度分析的边界条件，并且对每个自由度都使用一个弹簧单元，弹簧单元刚度的选取依赖于张力腿自身的属性而定［13］.使用SESAM软件中的Genie模块，得到平台的有限元模型，如图2所示.

图2　张力腿平台的有限元模型Fig.2 Finite element model of TLP

2） 疲劳分析关键节点的选取

根据整体结构有限元分析结果，选取以下8个典型节点进行疲劳校核.节点1～4为立柱与两侧浮箱上表面相交的4个角点，如图3所示.节点5～8为水线面处立柱外板、内外立柱支撑板和环形T型材的交汇处，如图4所示，节点5更详细的位置可参照图5.

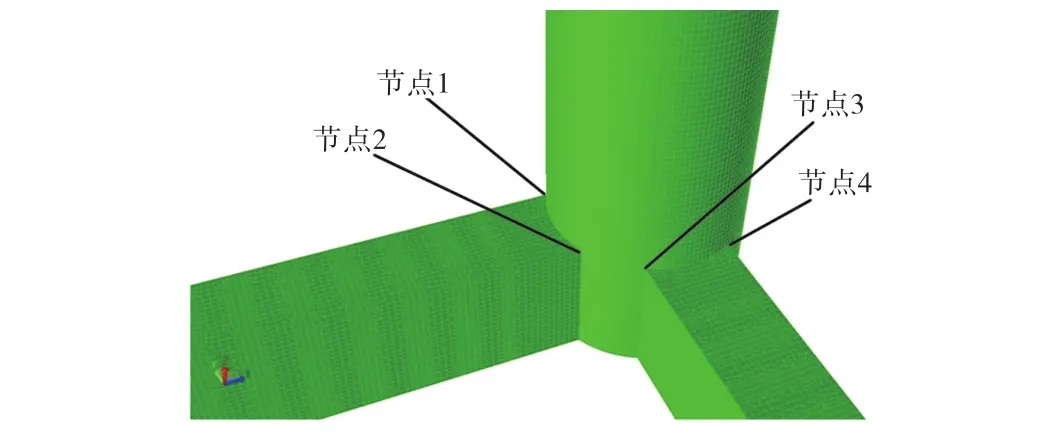
图3　节点1～4的位置Fig.3 Location of joints 1—4

图4　节点5～8位置Fig.4 Location of joints 5—8

2.3关键节点的应力传递函数

使用SESAM软件中的HydroD模块进行水动力计算，根据相关规范［14］推荐，总共选取了0°～180°、步长为30°的7个波浪方向，浪向均匀分布.波浪频率区间为0.25～2.00,rad/s，步长为0.05,rad/s，共计36个波浪频率.所以，总共的计算工况达252个.

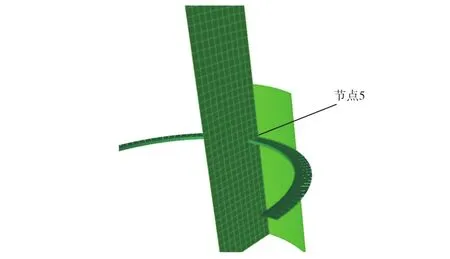
图5　节点5更为精确的位置Fig.5 Accurate location of joint 5

仅以节点1和2为例，给出在不同浪向下的应力传递函数，如图6和图7所示.

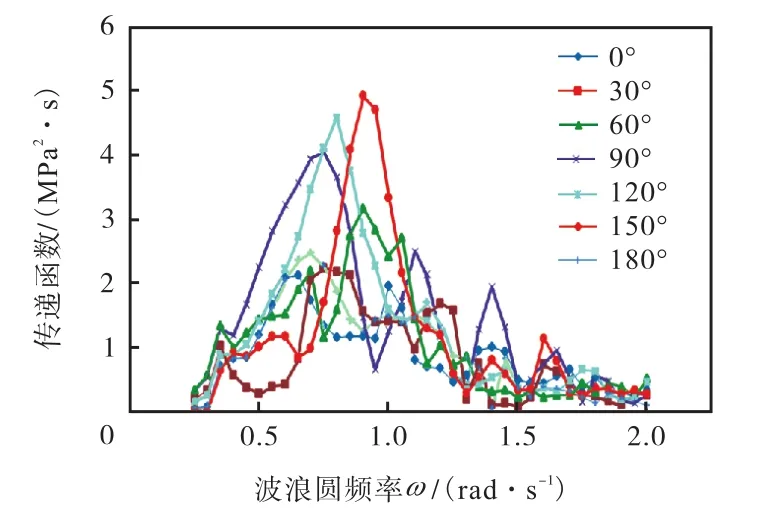
图6　节点1的应力传递函数Fig.6 Stress transfer functions of joint 1

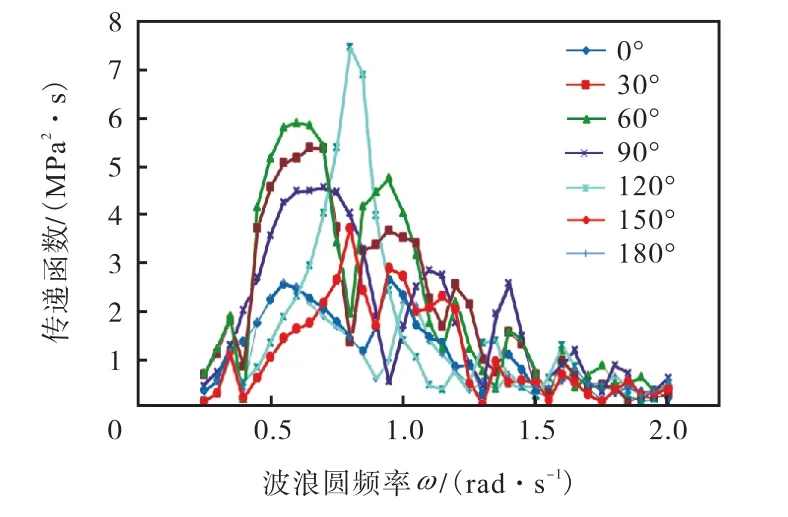
图7　节点2的应力传递函数Fig.7 Stress transfer functions of joint 2

3　基于累积损伤的TLP疲劳可靠性分析

3.1波浪散布图和短期海况的选取

波浪散布图中，每一海况由表征波浪特征的参数有义波高HS、平均跨零周期TZ以及该海况出现的频率来描述.选取南海某海域的波浪散布图，从中选取频率较大的海况，最终选定了24种短期海况，在总海况中的比重达到了95.7%,，能够比较理想地代表该海域的海况，24个短期海况如表2所示.

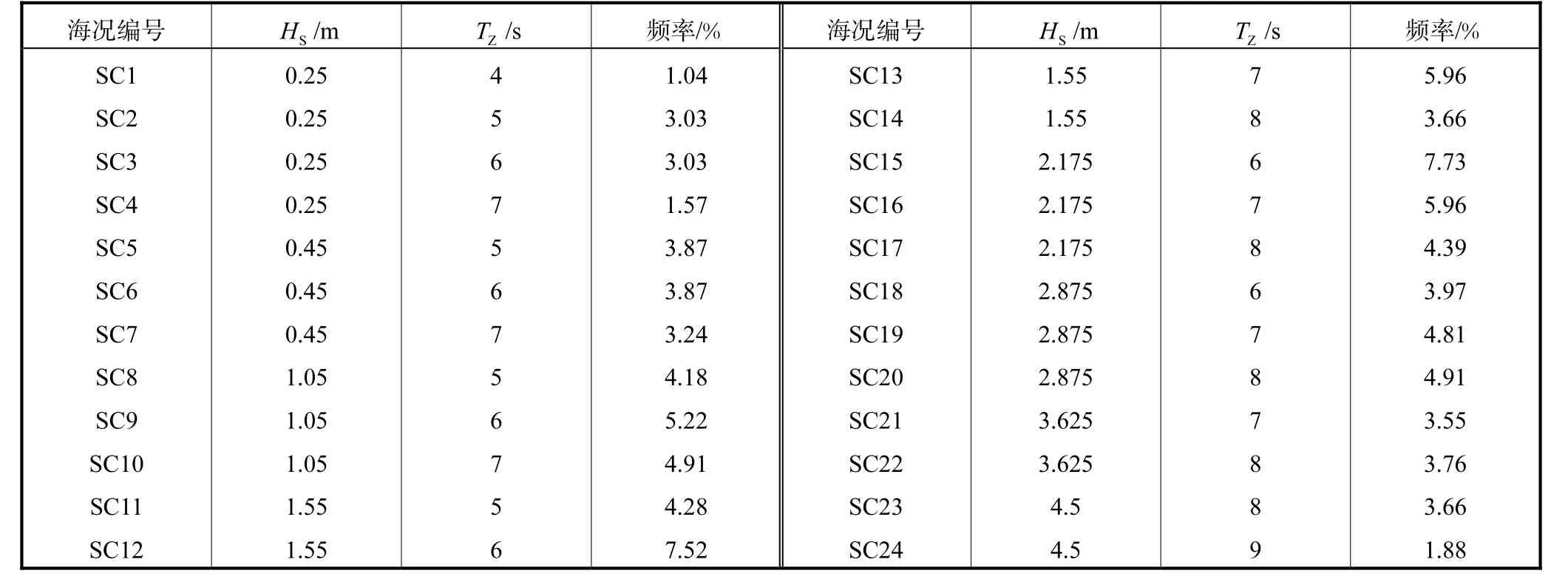
表2　24个短期海况Tab.2 Twenty-four short conditions

3.2波浪谱的选取

波浪谱取JONSWAP谱，采用波高和波浪周期表示的谱公式

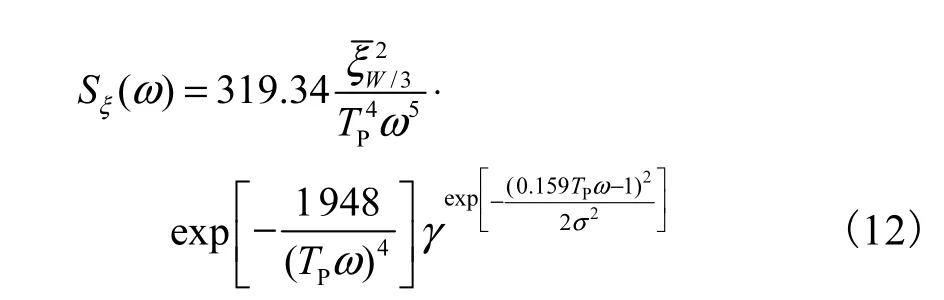
根据波浪散布图和选择的波浪谱，便可以得到24种短期海况的JONSWAP谱.

3.3生成关键节点的疲劳应力谱

于是，每个节点共有168条疲劳应力谱，加上之前确定的8个关键节点，那么共计需要生成1,344条疲劳应力谱曲线.

图8和图9给出了节点1在海况21（SC21）和海况22（SC22）时7个方向的应力谱密度.

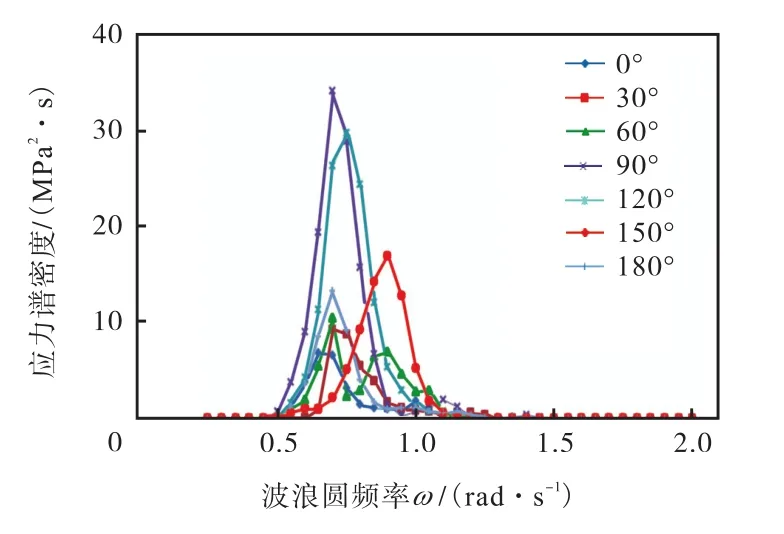
图8　节点1在海况21时的应力谱密度Fig.8 Stress spectral density under SC21 for joint 1

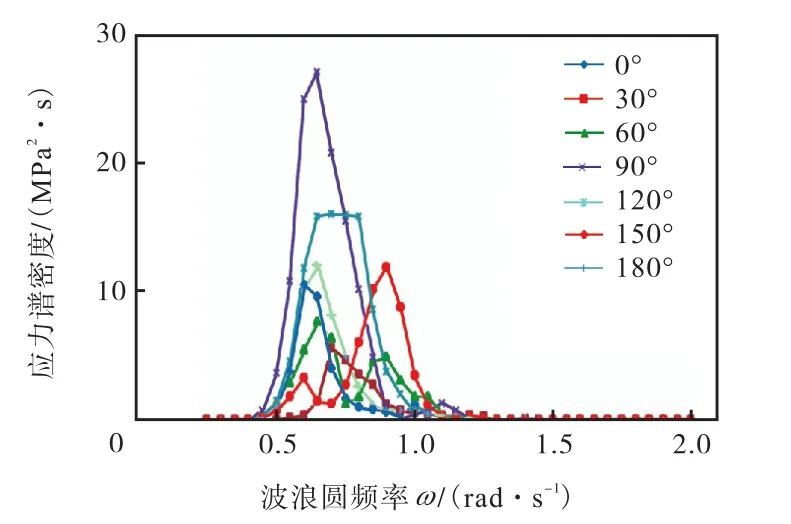
图9　节点1在海况22时的应力谱密度Fig.9 Stress spectral density under SC22 for joint 1

3.4S-N曲线的选择

本文计算的相关参数参考ABS的规范，对于非管节点，空气中和海洋环境有阴极保护下的结构的S-N曲线如表3所示.

表3　S-N曲线Tab.3 S-N curve

对于节点1～4选择ABS-（CP）非管节点曲线，对于节点5～8选择ABS-（A）非管节点曲线.

3.5疲劳寿命可靠度的计算结果

S-N曲线中随机变量A的中值和变异系数的选取参考ABS的规范［15］.而根据Wirsching等［16］的研究，可以得到疲劳损伤度Δ和参数B的中值与变异系数，最后的取值如表4所示.

表4　随机变量的中值和变异系数Tab.4 Mean and coefficient of variation of random variables

带入之前推导的可靠性计算公式，可以得到节点1～8的可靠性指标，如表5所示.

表5　8个节点可靠性的最终计算结果Tab.5 Final computing results of reliability of 8 joints

4　基于累积损伤的TLP时变可靠性分析

根据文献［17］，计算结构性能的时变性时，须对S-N表达式进行修正.本文引入疲劳累积损伤增加函数α（n），采用幂函数模型，对疲劳累积损伤指数按使用年限做适当提升，即

式中：D（n）、D（0）分别为第n年和最初的累积损伤；TD为设计寿命，本文为20年.根据Qin等［18］提出的船舶与海洋结构腐蚀衰减模型和总结出的平台抗力衰减规律，假设结构达到设计寿命时的累积损失增加了30%，取0.14k=.使用上述公式，便可以得到各关键节点在设计寿命期内的疲劳可靠性指标，结果如表6所示.

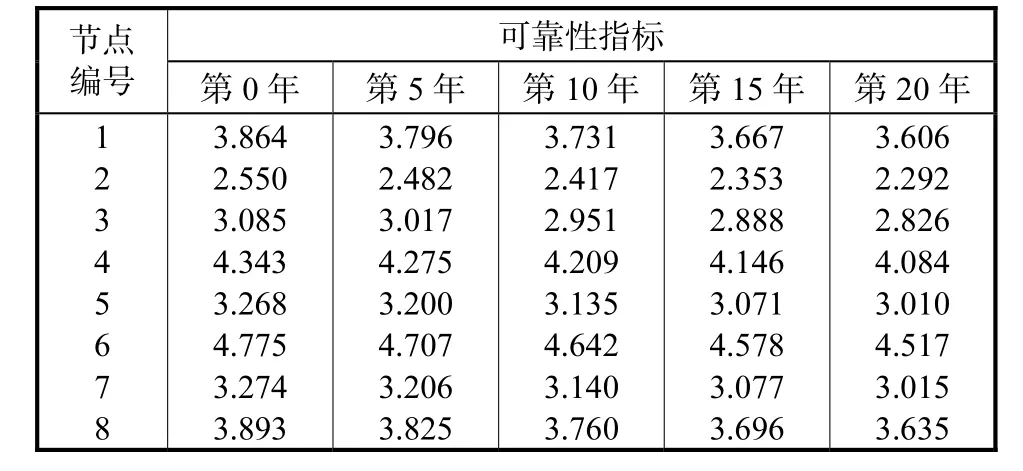
表6　各时间段的可靠性指标Tab.6 Reliability index during each period

5　结　论

（1） 本文建立了TLP的整体结构模型，求出不同工况下的应力传递函数.结合南海海况，基于累积损伤理论得到平台关键部位的疲劳可靠性，以保证工程安全.

（2） 疲劳可靠性具有时变性，引入疲劳累积损伤增加函数，从而得到平台各关键部位随时间而变化的疲劳可靠度.可以看到，在平台设计期内，可靠性指标均大于2，符合实际工程的要求，本方法可为所有海洋结构物的设计和建造提供参考.

［1］ 王 屹，李小森. 天然气水合物开采技术研究进展［J］. 新能源进展，2013，1（1）：69-79. Wang Yi，Li Xiaosen. Research progress of natural gas hydrate production technology ［J］. Advances in New and Renewable Energy，2013，1（1）：69-79（in Chinese）.

［2］ Zeng Xiaohui，Yu Yang，Zhang Liang，et al. A new energy-absorbing device for motion suppression in deepsea floating platforms ［J］. Energies，2015，8：111-132.

［3］ Zhang Liang，Wu Han，Yu Yang，et al. Axial and transverse coupled vibration characteristics of deep-water riser with internal flow ［J］. Procedia Engineering，2015，126：260-264.

［4］ Siddiqui N A，Ahmad Suhail. Fatigue and fracture reliability of TLP tethers under random loading ［J］. Marine Structures，2001，14：331-352.

［5］ 余建星，张中华. 波、流联合作用下张力腿平台系索系统疲劳可靠性分析方法研究［J］. 海洋技术，2009，28（2）：69-72. Yu Jianxin，Zhang Zhonghua. Research on fatigue reliability of tension leg platform tendon system under wave and current ［J］. Ocean Technology，2009，28（2）：69-72（in Chinese）.

［6］ 杨 鹏. 半潜平台结构疲劳可靠性评估方法研究［D］.北京：中国舰船研究院，2012. Yang Peng. Research on Reliability Assessment Method for Structural Fatigue of Semi-Submersible Platform［D］. Beijing：China Ship Research and Development Academy，2012（in Chinese）.

［7］ 崔 磊. 深水半潜式平台疲劳分析及关键节点的疲劳试验研究［D］. 杭州：浙江大学建筑工程学院，2013. Cui Lei. Fatigue Analysis of Deepwater Semi-Submersible Platform and Fatigue Test on Key Joint ［D］. Hangzhou：School of Civil Engineering，Zhejiang University，2013（in Chinese）.

［8］ 林 红，陈国明. 考虑多失效模式老龄平台结构可靠性分析［J］. 中国石油大学学报：自然科学版，2010，34（4）：107-112. Lin Hong，Chen Guoming. Reliability analysis for aging offshore platforms considering multi-failure modes［J］. Journal of China University of Petroleum，2010，34（4）：107-112（in Chinese）.

［9］ Akgul F，Frangopol D M. Computational platform for predicting lifetime system reliability profiles for different structure types［J］. Journal of Computing in Civ Eng，2004，18（2）：92-104.

［10］ Stewart Mark G. Reliability safety assessment of corroding reinforced concrete structures based on visual inspection information［J］. ACI Structural Journal，2010，107（6）：671-679.

［11］ 胡毓仁. 船舶与海洋工程结构疲劳可靠性分析［M］.哈尔滨：哈尔滨工程大学出版社，2010. Hu Yuren. Ship and Ocean Engineering Structural Fatigue Reliability Analysis［M］. Harbin：Harbin Engineering University Press，2010（in Chinese）.

［12］ 中国船级社. 海上移动平台入级与建造规范［S］. 北京：人民交通出版社，2005. CCS. Rules for Construction and Classification of Mobile Offshore Drilling Units［S］. Beijing：The People's Communications Publishing House，2005（in Chinese）.

［13］ 李 辉. 张力腿平台水动力响应与总体强度研究［D］.哈尔滨：哈尔滨工程大学船舶工程学院，2012. Li Hui. Tension Leg Platform Hydrodynamic Response and Global Strength Research［D］. Harbin：School of Naval Architecture，Harbin Engineering University，2012（in Chinese）.

［14］ ABS 6—2008 Rules for Building and Classing Mobile Offshore Drilling Unit［S］. New York：American Bureau of Shipping，2008.

［15］ ABS Guide for the Fatigue Assessment of Offshore Structures［S］. New York：American Bureau of Shipping，2003.

［16］ Torng T Y，Wirsching P H. Fatigue and fracture reliability and maintainability process［J］. ASCE，J Struct Eng，1991，117（12）：3804-3822.

［17］ 李桂青. 工程结构时变可靠度理论及其应用［M］. 北京：科学出版社，2001. Li Guiqing. The Theory and Its Application on Time-Dependent Reliability of Engineering Structures［M］. Beijing：Science Press，2001（in Chinese）.

［18］ Qin Shengping，Cui Weicheng. Effect of corrosion models on the time-dependent reliability of steel plated elements［J］. Marine Structures，2003，16（1）：15-34.

（责任编辑：赵艳静）

Fatigue Reliability and Time-Dependent Reliability Assessment on TLP Based on Cumulative Damage Theory

Yu Jianxing1,2，Liu Jie1,2，Yu Yang1,2，Huang Fuxiang3，Fan Zhiyuan1,2，Wang Huakun1,2
（1.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China；3.Offshore Oil Engineering Company Limited，Tianjin 300451，China）

Tension leg platform（TLP）is vulnerable to considerable fatigue damage over its design life period under severe sea conditions and alternating loads and thus fatigue damage is an important aspect of structural failure.Firstly，spectral analysis method was employed，based on cumulative damage theory，to systematically study the fatigue reliability of the key parts of the platform.Then，the whole structural model was built and the stress transfer functions of key joints under working conditions were obtained.At the same time，the fatigue cumulative damage increasing function was introduced to analyze the time-dependent reliability of the key parts.Finally，the time-dependent reliabilities of the key parts of TLP were obtained，and applicability and reliability of the method were then verified by specific examples.

tension leg platform（TLP）；fatigue reliability；cumulative damage；spectral analysis method；timedependent reliability

P751

A

0493-2137（2016）09-0896-06

10.11784/tdxbz201601047

2016-01-12；

2016-03-11.

国家重点基础研究发展计划（973计划）资助项目（2014CB046803）；国家自然科学基金资助项目（51239008，51379145）；上海交通大学国家重点实验室开放基金资助项目（1502）.

余建星（1958— ），男，教授，博士生导师.

余建星，yjx2000@tju.edu.cn.

网络出版时间：2016-04-29. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20160429.1030.006.html.