基于混沌遗传算法的永磁无刷电机优化设计研究
赵阳阳,闫鸿魁,王 森,杨秀敏,郭嘉成
(沈阳工程学院 a.电力学院;b.自动化学院,辽宁 沈阳 110136)
基于混沌遗传算法的永磁无刷电机优化设计研究
赵阳阳a,闫鸿魁b,王森b,杨秀敏b,郭嘉成a
(沈阳工程学院a.电力学院;b.自动化学院,辽宁 沈阳 110136)
以永磁无刷直流电机为研究对象,介绍了遗传算法中的自适应交叉和自适应变异,在此基础上,提出了一种应用于永磁无刷直流电机的新型混沌遗传优化算法。给出了遗传算法操作设计步骤和永磁无刷电机优化设计的流程图,完成了混沌遗传算法优化设计的理论推导。利用MATLAB软件对优化算法进行编程和仿真分析,得到电机优化前后参数对比表和混沌遗传算法寻优跟踪图,结果显示新型混沌遗传优化算法迭代次数短,优化效果好,可以为永磁无刷电机优化设计提供理论参考。
永磁无刷电机;混沌;遗传;优化设计
电动汽车和电动飞机领域是当前两大新型研究方向,未来有巨大的发展潜力。由于其低廉的成本和优越的性能,经常采用永磁无刷电机作为电动汽车和电动飞机的主推进源。国内外专家学者采用不同的算法对永磁无刷电机本体进行优化设计,力争追求最优的电机性能,常用的电机优化算法为遗传算法[1-5]、混沌算法[6-7]及其衍生算法[8-9]。
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索的最优解方法。但在实际应用中,遗传算法容易产生早熟收敛的问题,不利于问题的求解。混沌算法是将混沌空间的变量切换到解空间,进而完成动力学方程式的求解,是一种新型搜索算法。通过混沌变量的特点进行搜索,混沌优化方法具有对初值敏感、局部极小点易跳出、全局渐进收敛和搜索速度快的特点。
1 自适应交叉和自适应变异
在遗传算法中,影响算法收敛性、遗传算法行为和性能的关键所在是如何选择交叉概率Pc和变异概率pm。交叉概率Pc与新个体产生速度成正比,但是大到一定程度时,交叉概率Pc又与模式的破坏可能性成正比,导致高适应值的个体结构很快被破坏,搜索过程将变得缓慢,最终早熟停止。产生新个体结构的难易程度取决于变异概率pm,越小越难产生。根据交叉概率和变异概率的收敛状态,进行自适应变化以克服局限性,即简单遗传算法中交叉概率和变异概率在简单遗传算法中固定不变,这保证了进化前期的快速搜索以及个体的多样性。自适应交叉概率变化公式为
(1)
式中,fc是2个个体交叉后较大的适应值,fav是上代平均适应值,fmax是上代最大的适应值。
当要交叉的2个个体适应度都较低时,若小于上一代平均适应度,说明它们适应度很差,以概率1交叉以便获得更高适应度的新个体;当交叉的2个个体较大适应值大于fmax时,说明此个体适应度很高,不需要交叉,通过最优的保留策略,直接复制到下代;当fc介于fav和fmax之间时,采用自适应变化的交叉概率,即比平均概率大得越多,交叉概率越小,以此来降低优秀个体被破坏的概率。
自适应变异概率变化可表示为
pm=pm1+(pm2-pm1)×t/tmax
(2)
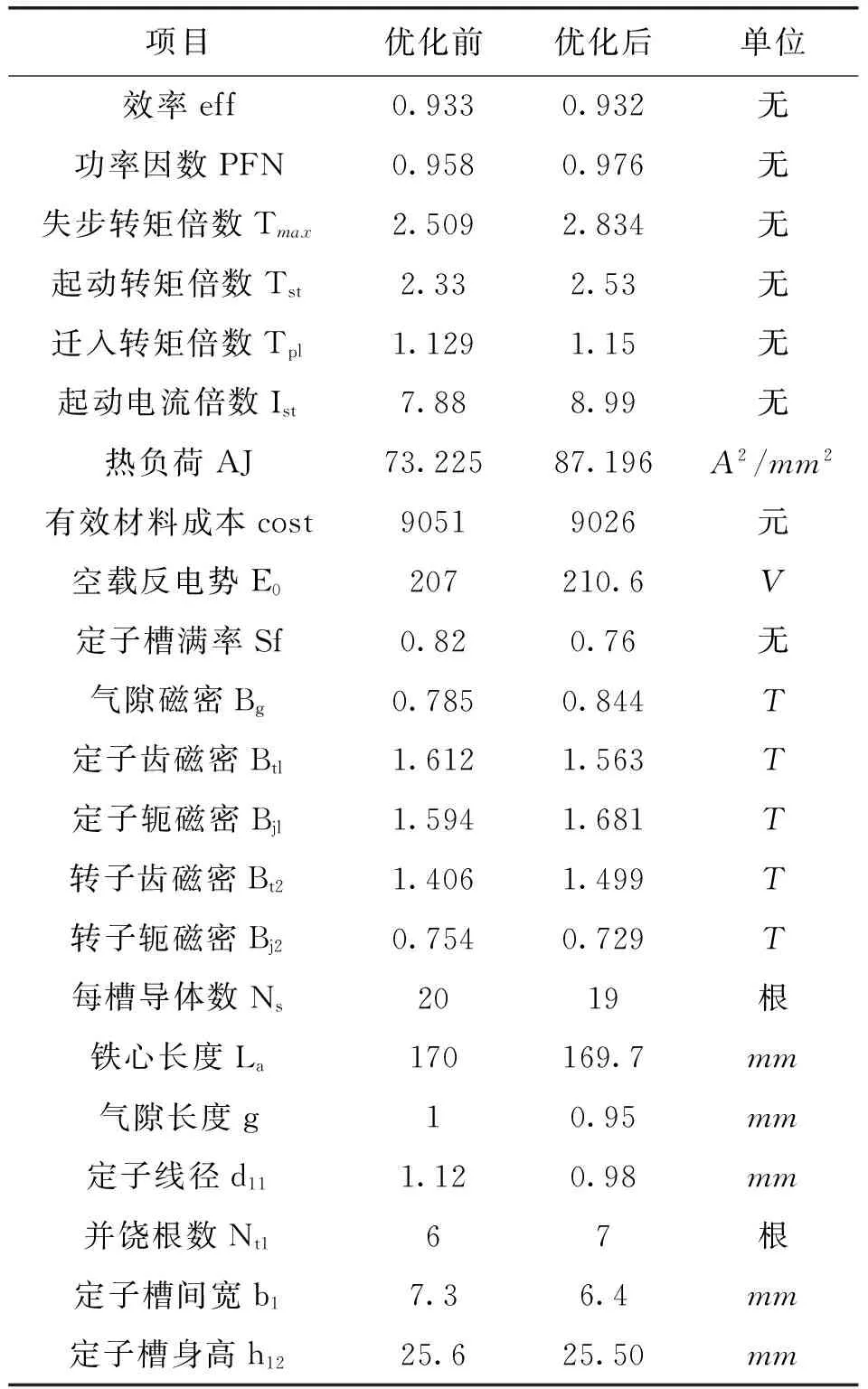
式中,tmax是最大进化代数,pm是第t代个体的变异概率,pm1、pm2分别是初始和末代的变异概率,且满足pm1 在交叉和变异概率中,其数值的自适应改变确保进化初期可产生大量新个体,多样性丰富的必要条件,又满足了后期优秀个体被破坏可能小的要求,极利于需求最优解。 2.1遗传算法设计 遗传操作设计以永磁直流无刷电机为研究对象,包括编码及译码、初始种群的产生、选取、交叉以及变异。 根据遗传算法的易操作性和二进制编码、解码的灵活性,采用了二进制编码。根据离散化精度和变化范围,将8个优化变量编码成长度不同的二进制子串按顺序连接形成一个个体。 考虑尽可能降低计算量、均衡每个优化变量的编码长度和考虑加工工艺精度等几个方面的因素,对优化变量的离散化步长(单位:mm)作如下定义: scale=[1,1,0.35,0.1,0.1,0.1,0.1,0.05] (3) 式(3)中对应的各优化变量: X=[Ns,Nt1,La,bM,hM,b1,h12,g] (4) 式中,Ns为每槽导体数,Nt1为并饶根数,La为铁心长度,bM为永磁体宽度,hM为永磁体磁化方向长度,b1为定子槽肩宽,h12为定子槽身高,g为气隙磁密。 上述优化变量编码采用如下的函数: (5) 式中,ceil是取整数函数,randint是产生一定位数矩阵的函数。 由于永磁无刷电机导线直径是非均匀变化的,所以独立编码。通过读取初始方案值周围的8种线规,其整数编号为0,1,2,…,7。编号与绕组线径成正比,优化变量的线径对应编码串长为3位,编码成000~111间的编码。 二进制的染色体转化为设计优化变量数值过程称为译码。对于连续均匀离散化变量,解码值通过二进制与十进制的对应关系获得;对于导线直径,由编码转换成数得到导线的序号,然后根据序号与导线直径的对应关系,得到导线直径。译码结束需要生成初始种群。 在生成初始种群前,需要确定种群规模大小popsize。群体领域与群体中个体的多样性成正比,与算法陷入局部最优解的可能性成反比。同时,群体规模与计算量成正比,与优化的速度直接关联。 在确定种群规模大小后,把永磁无刷电机的初始方案编码作为种群的一个个体,因为是在初始方案的基础上进行的永磁无刷电机的优化设计,在可行领域内对应的点是其优化设计变量数值,性能的各项技术指标相对较好。 个体适应度值与决定其在下一代中得到繁殖的机会概率成正比称之为选择操作。适应度与被选择的概率成正比。选择概率的计算方法如下: (6) 交叉分为一点交叉和N点交叉,两个交叉的个体部分基因片段互换,是新个体产生的主要原因。采用一点交叉方式,交叉过程如图1所示。 图1交叉过程 随着适应度的不断提高,交叉概率在不断减小,同一代种群中充斥大量相同的个体,在遗传算法后期,算法处于停滞状态,几乎丧失搜索能力。引入变异算子的目的是保持群体中个体的多样性并增强遗传算法的搜索能力。 对染色体中每一位,随机数δ在[0,1]区间产生,变异是否发生取决于δ和pm的大小,若Pm≥δ,则该位由0至1或由1至0;若Pm<δ,则该位保持原基因值,如图2所示。 图2变异过程 以上具体探讨了改进遗传算法用于永磁无刷电机设计中涉及到的一些遗传操作的具体设计问题。这些为实现直线式永磁同步电机优化程序的编制奠定了坚实的基础。 2.2优化软件设计 图3是基于改进遗传算法的永磁同步电机的优化程序流程图。优化设计程序采用MATLAB语言编制。程序采用模块化设计,兼容性强,思路缜密,为功能的扩展奠定了良好的基础。 该优化程序主要包括初始数据输入模块、永磁无刷电机电磁计算程序、交叉算子、变异算子、选择算子、结果输出模块等。该优化程序已经调试成功,可以用于优化设计。 图3 电机优化流程 2.3混沌遗传算法优化设计 假定连续优化问题可描述为以下形式: minf(x1,x2,x3,…,xn), xi∈[ai,bi],i=1,2,…,n (7) 遗传和混沌优化方法由于其内在的算法结构,差别很大的是检索粒度和映射方式,在遗传算法中是将原问题的解空间映射到编码空间,设xi∈[ai,bi],用m位二进制编码,xi检索结果精度达(bi-ai)/2m,搜索粒度达(bi-ai)/2m。为提高搜索精度,编码位数必然要提高,因而运算次数将会增加。因此,遗传算法要综合考虑精度和算法复杂度双因素。而混沌优化算法是将混沌区域反映到原问题解空间,通过自身变量的内在特性而进行整体性扫描。在实际情况下,混沌空间大小是有局限性的,如式(8)Logistic映射: tk+1=μtk(1-tk) (8) 式中,μ是支配参考量,取μ=4,设0≤t1≤1,k为正整数,当μ=4时,系统体现为混沌状态,其混沌空间为[0,1],设原问题解空间范围为li,精度设为0.001,则混沌优化搜索精度为li×0.001。原问题解空间与混沌优化的搜索精度成反比。混沌优化会出现失效的情形同原问题解空间的大小有关,为了避免这种情况,可采用遗传混沌优化组合算法。遗传算法采用二进制编码,把xi的取值周期线性反映到长为li的二进制位串,搜索粒度设为θ,则该问题的一个可行解对应为∑li=1的二进制位串。在杂交时选用离散杂交,杂交点选在各变量的子位串的特定位上。混沌优化方法选用式(8)的Logistic映射所产生的混沌空间。 遗传混沌优化组合算法的过程如下: 1)随机选取m个二进制位串作为初值,置p=0; 2)求取二进制位串在原解空间所对应值,并求取fj(=1,2,3,…,m),设 为适应度函数,如果所取的随机数小于适应度函数,则新的随机产生的长为l的二进制位串替代该位串; 3)对于前k(1≤k 4)对所有的位串实现自适应位变异算法,对每个变量而言,在所有的循环次数内,实行变异算法的位数逐步从最高位到最低位; 7)确定搜索张度σ=(σ1,σ2,…,σn),x-σ0/2,x+σ0/2为搜索空间。对混沌变量进行如下线性变换,目的是实现混沌变量从混沌空间和问题解空间的转换: 10)置k=k+1,转第7步,搜索m步后,f*维持不变,最终结束。 由于遗传算法搜索得到的粗解和精确解分布的位置不同,并且搜索粒度θ为遗传算法的位串之间的最小Hamming距离,所以算法的有效性需要保证,搜索张度必须满足σi≥2。 为了验证算法的正确性,采用MATLAB编程,完成22kW永磁无刷电机优化设计。其中,种群领域popsize=40,pc1=0.95,pc2=0.5,pm1=0.001,pm2=0.01,进化最大代数设置为generation=100。 表1列出了永磁无刷电机优化前后的数据对比情况,迭代次数选为100次。从表1可看到电机参数优化后,功率因数PFN、失步转矩倍数Tmax、 起动转矩倍数Tst、牵入转矩倍数Tpi有了提高,电机的有效材料成本降低了几十元。虽然效率在降低,起动电流倍数和热负荷有所上升,但仍然处于合理范围之内。总体来看,优化效果很明显。 图4为遗传算法寻优跟踪图,经过100次迭代,种群个体的最大适应度、平均适应度都在平稳地增加。在混沌遗传算法后期,种群中最佳个体适应度保持在一个平衡点,因此认为最优结果已产生,终止优化。 表1 22 kW永磁无刷电机优化前后性能变化表 图4 遗传算法迭代100次寻优跟踪 提出的用于永磁无刷电机优化设计的混沌遗传优化算法的搜索效率和精度均较高,可以使优化变量的搜索空间减小,变量的搜索精度能够得以加深,充分发挥了遗传算法和混沌算法的优点,算法的提出为永磁电机本体优化设计更好、更快地发展奠定了理论基础。新型算法编程简单,通俗易懂,优化算法有代表性和可扩展性,连续对象优化的有效性通过MATLAB仿真实例得到了验证。 [1]张桂臣,马捷.船舶电力推进SSP电机应用IGA-ANFIS优化控制[J].电机与控制学报,2011,15(11):73-78. [2]陈云云,全力,朱孝勇,等.双凸极永磁双转子电机优化设计与电磁特性分析[J].中国电机工程学报,2014(12):1912-1921. [3]ArabaliA,GhofraniM,Etezadi-AmoliM,etal.Genetic-Algorithm-BasedOptimizationApproachforEnergyManagement[J].IEEETransactionsonPowerDelivery,2013,28(1):162-170. [4]HasanienHM,Abd-RabouAS,SakrSM.DesignOptimizationofTransverseFluxLinearMotorforWeightReductionandPerformanceImprovementUsingResponseSurfaceMethodologyandGeneticAlgorithms[J].IEEETransactionsonEnergyConversion,2010,25(3):598-605. [5]OkamotoY,TominagaY,WakaoS,etal.TopologyOptimizationofRotorCoreCombinedWithIdentificationofCurrentPhaseAngleinIPMMotorUsingMultistepGeneticAlgorithm[J].IEEETransactionsonMagnetics,2014,50(2):725-728. [6]鲍晓华,王群京,倪有源,等.爪极发电机建模及参数优化设计[J].中国电机工程学报,2006,26(21):138-142. [7]ZhuMin,YangChun-ling,LiWei-liang.AutotuningalgorithmofparticleswarmPIDparameterbasedonD-Tentchaoticmodel[J].JournalofSystemsEngineeringandElectronics,2013,24(5):828-837. [8]韩力,罗张尧,金钊,等.定子双绕组风力感应发电机优化设计方法[J].电力自动化设备,2015,35(3):33-40. [9]JollyL,JabbarMA,LiuQ.Designoptimizationofpermanentmagnetmotorsusingresponsesurfacemethodologyandgeneticalgorithms[J].IEEETransactionsonMagnetics,2005,41(10):3928-3930.OptimizationDesignofPermanentMagnetBrushlessMotorBasedonChaosGeneticAlgorithm (责任编辑佟金锴校对张凯) ZHAOYang-yanga,YANHong-kuib,WANGSenb,YANGXiu-minb,GUOJia-chenga (a.GraduateDepartment;b.SchoolofAutomation,ShenyangInstituteofEngineering,Shenyang110136,LiaoningProvince) Inthispaper,theadaptivecrossandadaptivemutationofthegeneticalgorithmwereintroduced.Onthebasis,anewchaosgeneticoptimizationalgorithmappliedinpermanentmagnetbrushlessdcmotorwaspresented.Theoperationdesignstepsofgeneticalgorithmanddesignflowchartofpermanentmagnetmotorwereshowed,andthen,thetheoreticalderivationofoptimizationdesigninchaosgeneticoptimizationalgorithmwasillustrated.ThemotorparametercomparisontablebeforeandafteroptimizationandtheoptimaltrackingfigureofchaosgeneticalgorithmwasobtainedbyMATLABsimulation.Theresultsshowedthatthenewchaosgeneticoptimizationalgorithmhadlesseriterationsandbettereffect.Thispaperprovidesatheoreticalreferenceforoptimizationdesignofmainpropulsionpermanentmagnetmotor. permanentbrushlessmotor;chaos;genetic;optimizationdesign 2015-11-06 辽宁省教育厅项目(L2015374);博士启动基金(201501088) 赵阳阳(1990-),男,河北衡水人,硕士研究生。 闫鸿魁(1982-),男,辽宁沈阳人,讲师,硕士。 10.13888/j.cnki.jsie(ns).2016.03.009 TM341 A 1673-1603(2016)03-0234-052 永磁直流无刷电机混沌遗传算法设计

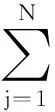




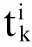
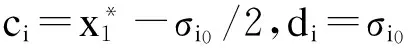


3 仿真分析

4 结 语

