结构化填充床内流体流动的三维数值研究

刘　洋，史俊瑞，李　楠，夏永放，徐有宁

(沈阳工程学院 a.能源与动力学院;b.沈阳市循环流化床燃烧技术重点试验室，辽宁 沈阳 110136)



结构化填充床内流体流动的三维数值研究

刘洋ab，史俊瑞b，李楠b，夏永放b，徐有宁b

(沈阳工程学院 a.能源与动力学院;b.沈阳市循环流化床燃烧技术重点试验室，辽宁 沈阳 110136)

流体在多孔介质空隙内的流动非常复杂，采用常规的实验方法，测量流速分布的数据非常有限，并且有可能破坏流场结构。为了研究不同Re下，结构化填充床流通区域内不同截面的流速分布情况，采用CFD方法进行数值研究，定量分析孔隙内的流动特性。研究结果表明：在层流范围内，当Re较小时，随着流通截面积的增大，流速降低得非常明显，粘性力起主要作用；当Re增大到204.74时，流速降低的速度不再明显，此时惯性力在流动过程中起主导作用，数值模拟结果与实验值取得了定性的一致。

多孔介质；数值研究；层流；填充床

填充床是一个非均相体系，由固体颗粒和颗粒空隙间的流体组成，颗粒堆积在一定形状的容器或限定范围内。根据填充床的物理性质，可将填充床看作是由固体颗粒组成的骨架和由骨架分隔成的大量密集成群的微小孔隙所构成的物质。

多孔介质具有较好的蓄热传热能力、相间强烈的传质特性和优良的过滤特性。多孔介质填充床广泛应用于加热器、反应器、换热器和燃烧器等设备中，多孔介质中的传热传质和燃烧一直是研究的热点之一。但由于多孔介质的结构复杂，研究中对多孔介质的详细结构做了大量的简化，甚至通过经验公式考虑多孔结构对流体输运过程的影响[1-2]，因此可能造成很大的误差，甚至产生定性的失真。随着数值计算模型和方法的不断完善、发展以及高性能计算机的涌现，对于孔隙尺度的微观研究方法得到了迅猛的发展，数值计算将成为揭示微孔内流动、传热传质和燃烧的有力工具[3]。

Suekane等[4]采用核磁共振成像技术研究了简单立方体均匀堆积填充床内的惰性流动特征，选取了沿着主流方向的第五单元作为特征单元，提供了孔隙内流场分布的详细信息。郭雪岩等[5]采用CFD模拟研究了由120个小球组成的小直径比固定床内的流动，发现壁面效应对随机固定床流量分配的影响大于对结构化固定床的影响，小Re范围内小直径比随机固定床和结构化固定床的压降明显大于Ergun公式的预测值。

1　数值模拟

1.1问题描述

以Suekane等[4]实验研究的简单立方体均匀堆积填充床为原型，流体通道由6层小球堆积成5个纵向布置的单元体，如图1所示。每个单元体由8个1/8小球组成，小球的直径为28 mm，堆积后的填充床尺寸为28 mm×28 mm×168 mm，填充床孔隙率为0.476。为了避免在小球接触点附近产生扭曲度较大的网格，将小球直径缩小为原直径的99%，小球之间留有0.01 d，即0.28 mm的距离。

图1　简单立方体均匀堆积填充床原型

1.2控制方程

鉴于填充床结构的对称性，为节省计算资源，沿纵向方向取其中的1/4作为研究对象。实验中，在进出口处采用了整流段，用以保证入口流场的均匀性[6]。对复杂的整流结构进行简化，计算区域分别向单元体上游和下游延伸3个小球长度，得到的计算域总体尺寸为14 mm×14 mm ×336 mm。

由于实验中的颗粒雷诺数较小，假设流动为层流且流体不可压缩，得到下面的控制方程[7]：

1)连续性方程

(1)

2)动量方程

P+μ(

(2)

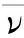
1.3边界条件

1.4求解过程

对于复杂的填充床结构，采用GAMBIT软件进行几何建模。由于孔隙尺寸变化大，计算区域全部采用适应性好的四面体网格。同时，由于局部孔隙间距狭小，采用size-function方法，对孔隙的网格进行加密处理[8]，如图2所示。为了方便比较，图2中给出了未划分网格的几何体。对所研究的问题进行网格无关性考核，在不同的网格数量下，对简单立方体的内部流动进行考核。网格数量共计258万，并获得了相应的无关解。计算基于CFD求解器FLUENT进行，压力与速度耦合采用SIMPLE算法[9]。

图2　单元体网格划分

2　结果与分析

2.1验证数值模型

当颗粒Re分别为12.17、28.88和204.74时，在第4个单元体中心(y=0.014 m，z=0.196 m)沿x轴的z方向无量纲速度(vz/vmean)实验值与模拟值的分布曲线如图3所示。其中，vmeam表示平均速度，vmeam=Q/Aε，Q指通过单元体的体积流量，A指单元体的横截面积，ε指孔隙率。从图3中可以看出，模拟数据与实验值吻合得较好。无量纲速度在x/r=0处的速度最大，即轴流速度在单元体中心速度最大，随着横坐标的增大或减小，无量纲速度降低，近似呈抛物线分布[10]。在Re=12.17时，速度变化较平缓，最大值为2.5左右，数值预测与实验值显示无回流；在Re=28.88时，速度变化比Re为12.17时稍大，在x/r=0处，实验值略高于模拟值，离散速度的最大值为3左右，在小球侧壁面无回流；在Re=204.74时，沿着x轴从单元体中心到小球壁面，流速变化较大，最大值为4左右，在x/r=0处，实验值略高于模拟值，在x/r=±0.8附近，实验值和模拟值都显示出了负数，说明此时产生了回流。总之，模拟值与实验值吻合的结果较好，从定量角度验证了模拟的准确性。

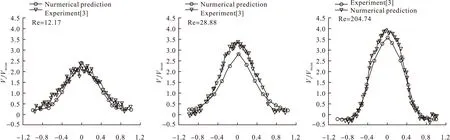
图3　沿x轴的vz/vmeam分布

2.2不同截面上的流速分布

当Re分别为12.17，59.78和204.74时，沿着z轴不同截面上的轴向速度分布如图4所示。在截面C(z/r=0.0)处，没有小球界面，流动区域充满了水；在截面A(z/r=-0.56)和E(z/r=0.56)处，在截面的4个角点处有4个小球界面，小球中心处的孔隙率为0.898；同样，在截面B(z/r=-0.28)和D(z/r=0.28)处，截面的4个角点处有4个小球界面，小球的中心处的孔隙率为0.694。结合实验值和数值模拟结果可以看出，当Re=12.17时，随着流通截面积的增加，流动速度降低，特别是对于z/r=-0.56处的截面，其效果更加明显；当Re=59.78时，随着流通截面积的增加，流动速度降低，但是降低的幅度并不明显，这说明随着雷诺数的增大，流动的惯性力相对增大，其中心处的速度受到边界层的约束而导致速度降低；当Re=204.74时，流速在不同截面上的速度降低幅度已经不再明显，说明惯性力在增强，小球表面对流动的约束在降低，且随着流速的增大，在侧壁面附近出现了回流，特别是对于z/r=0处的截面。比较模拟和文献中的图可以看出，数值模拟模型预测的结果和实验中得出的结果吻合，证明数值模型是有效的。

图4　不同截面轴向速度分布

3　结　论

1)在层流范围内，流通区域中间部位的流速达到平均流速的2倍以上；当Re数较小时，粘性力在流体的流动中起到主导作用，而惯性力的影响较小。

2)当Re=204.74时，在流通截面变化的情况下，沿着主流方向的速度变化不大，说明惯性力的作用在增强。

[1]史俊瑞，李本文，徐有宁，等.扩散过滤燃烧特性[J].化工学报，2012,63 (11)：3500-3505.

[2]夏永放，史俊瑞，徐有宁，等.燃烧模型对多孔介质内预混燃烧的影响[J].沈阳工程学院学报：自然科学版，2014，10(2)：118-122.

[3]WoodBD，ApteSV，LiburdyJA，etal.Acomparisonofmeasuredandmodeledvelocityfieldsforalaminarflowinaporousmedium[J].AdvancesinWaterResources,2015，85：45-63.

[4]SuekaneT,YokouchiY,HiraiS.Inertialflowstructuresinasimple-packedbedofspheres.FluidMechanicsandtransportphenomena[J],2003,41(9):10-17.

[5]GuoXue-yan，ChaoDong-hai，ChaiHui-sheng，etal.CFDanalysisofwalleffectsinpackedbedswithsmalltube-to-spherediameterratio[J].CIESCJournal，2012,63(1)：103-108.

[6]NijemeislandM.CFDstudyoffluidflowandwallheattransferinafixedbedofspheres[J].AICHEJournal,2006,50(5):906-921.

[7]杨 剑，周 觅，李师阳，等.三维颗粒有序列阵多孔介质湍流方程改进研究[J].工程热物理学报，2014,35(12)：42-47.

[8]NijemeislandM,DixonAG.ComparisonofCFDsimulationtoexperimentforconvectiveheattransferinagas-solidfixedbed[J].ChemicalEngineeringJournal,2001,82:231-246.

[9]DixonAG,NijemeislandM,SittEH.Systematicmeshdevelopmentfor3DCFDsimulationoffixedbeds:contactpointsstudy[J].ComputersandChemicalEngineering,2013,48:135-153.

[10]ChenKai，YuZhao-sheng，ShaoXue-ming.Directsimulationofnaturalconvectioninsquarecavityfilledwithporousmedia[J].JournalofZhejiangUniversity：EngineeringScience，2012,46(3):549-554.

(责任编辑张凯校对佟金锴)

ThreeDimensionalNumericalStudiesonFluidFlowinaStructuredPackedBed

LIUYangab,SHIJun-ruib,LINanb,XIAYong-fangb,XUYou-ningb

(a.CollegeofEnergyandPower;b.ShenyangKeyLaboratoryonCirculatingFluidizedBedCombustionTechnology,ShenyangInstituteofEngineering,Shenyang110136,LiaoningProvince)

Fluidflowintheporesofporousmediaisverycomplex.Thedataofflowdistributionintheporebythetraditionalexperimentalmethodisverylimitedandthismaydestroytheflowstructureunderthismethod.InordertostudytheflowvelocitydistributionintheregionindifferentcrosssectionofastructuredpackedbedatdifferentRenumber,thefluidflowinastructuredpackedbedwasstudiedusingCFDmethodandflowcharacteristicsintheporewereanalyzedwithquantitativeanalysis.ResultsshowthatthevelocitydecreasesgreatlyandtheviscousforceisdominantwhenincreasingtheflowareawithinthescopeoflaminarflowandasmallRenumber.WhentheReincreasesto204.74,thedecreaseinthevelocityisnotobviouslyobservedandtheinertialforceisdominantinthefluidflow.Thenumericalpredictionswereverifiedbytheexperimentalresults.< class="emphasis_italic">Keywords

:Porousmedia;numericalsimulation;laminar;packedbed

Porousmedia;numericalsimulation;laminar;packedbed

2016-02-29

国家自然科学基金资助项目(51406123)

刘洋(1992-)，女，辽宁瓦房店人，硕士研究生。

史俊瑞(1973-)，男，内蒙古包头人，副教授，博士，硕士生导师，主要从事低热值气体燃烧方面的研究。

10.13888/j.cnki.jsie(ns).2016.03.004

TQ051

A

1673-1603(2016)03-0208-05