球的接、切问题处理策略
安徽省太和中学 岳峻 韩长峰
球的接、切问题处理策略
安徽省太和中学 岳峻 韩长峰
从2016年起,安徽省高考不再是自主命题,而是采用全国Ⅰ卷,这是挑战,其中的一个挑战包括球的接、切问题。近十年安徽省自主命题一般不考查此类问题,但是这在全国Ⅰ卷属于必考知识点。作为一个不可小觑的考点,我们要了解球的概念,掌握球的性质,掌握球的表面积公式、体积公式,从而解决与球的截面有关的问题。
下面就球的接、切问题进行分类探讨,并给出相应的解决对策。
一、考查球的表面积、体积
策略 关键是由已知球的接、切信息的几何特征探求球的半径,然后代入相应的公式S球=,求解球的表面积和体积。
例1 设球的体积为V1,它的内接正方体的体积为V2,下列说法最合适的是( )。
A.V1比V2大约多一半 B.V1比V2大约多两倍半
C.V1比V2大约多一倍 D.V1比V2大约多一倍半

评注 本题利用球的直径亦即内接正方体的体对角线这一知识点,建立等量关系求得两个几何体的内在联系。
二、考查球的截面的性质
策略 球心与球的截面圆的圆心的连线垂直于该截面圆,球心与球面上任意一点所连的线段都是球的半径。这些性质是解决球的接、切问题过程中化空间为平面的根本依据。
例2 已知A、B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )。
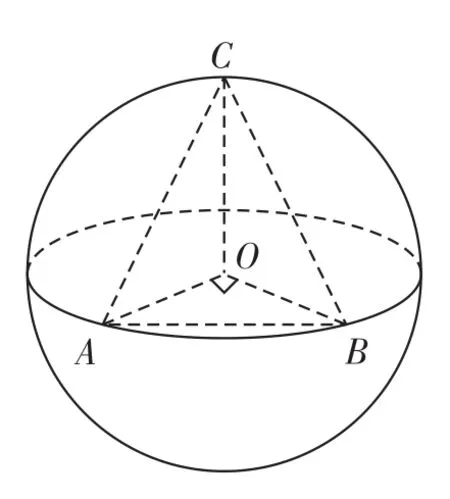
A.36π B.64π C.144π D.256π
解析 如右图所示,当点C位于垂直于平面AOB的直径端点时,三棱锥O-ABC的体积最大。设球O的半径为R,此时
解得R=6,所以球O的表面积为S=4πR2=144π。故选C。
评注 本题求三棱锥O-ABC体积的最大值时,灵活地借助于三棱锥的特性转化为求三棱锥C-AOB体积的最大值,是一个很好的策略。
例3 如右图所示,半径为R的球O中有一内接圆柱。当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是。
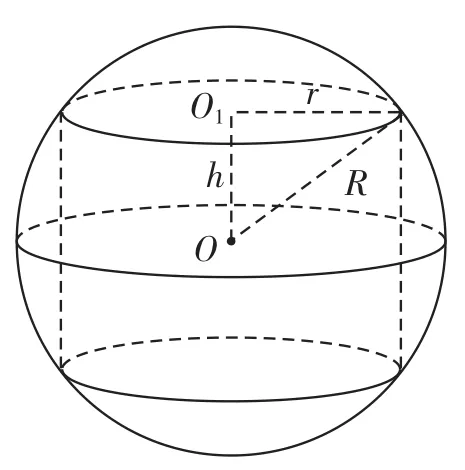
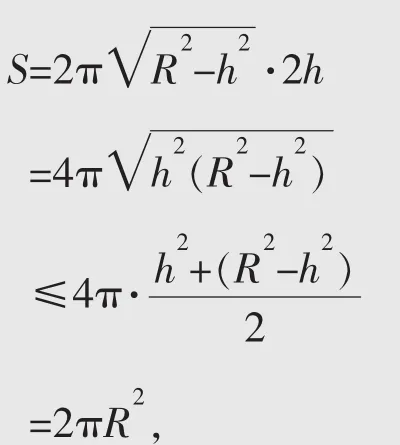
当且仅当h2=R2-h2,即2h2=R2时取等号。
故圆柱侧面积的最大值为2πR2。
此时球的表面积与该圆柱的侧面积之差是4πR2-2πR2=2πR2。故填2πR2。
评注 本题运用已知信息及圆柱体的有关性质,建立圆柱体侧面积关于球半径R的关系式,灵活应用基本不等式,求得圆柱的侧面积最大时R与圆柱体高h的关系。
三、考查与球有关的组合体
策略与球有关的组合体问题,一种是内切,一种是外接。解题时要认真分析图形,明确切点和接点的位置,确定有关元素之间的数量关系,并作出合适的截面图,常见的一些轴截面图如下:

内切问题的关键是抓住相切时的实质,即球心到切点的距离等于球的半径;外接问题的关键是抓住相接时的特征,即球心到接点(多面体的顶点)的距离等于球的半径。
例4 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )。


解析 如右图所示,设O为球心,PO=OA=R,OO1=x,

评注 本题巧妙运用正四棱锥的性质,确定其外接球的球心在它的高PO1上,进而建立直角三角形,解出球的半径,再求出球的表面积。
例5 如右图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )。


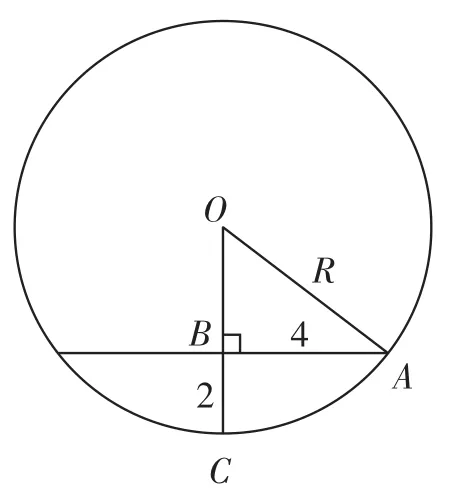
解析 设球的半径为R,则由题知,球被正方体上底面所在平面截得圆的半径为4,球心到截面圆的距离为R-2,球平行于正方体侧面的轴截面如右图所示,△OBA为直角三角形,
则R2=(R-2)2+42,解得R=5,
评注 球与多面体间的“切”的问题,关键突破口是作出过它们的切点且与轴截面重合的一个截面,将空间问题转化为平面问题解决,在计算过程中要抓住球半径这个主要元素。

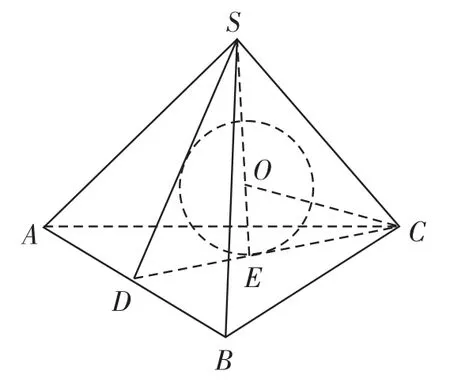
解析 如右图所示(部分线段未画出),设球心为O,正方形ABCD的中心为O1,

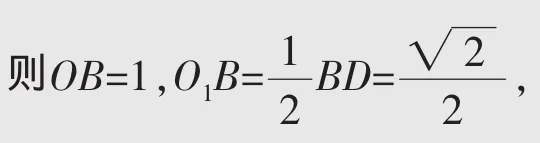
易知SO2为线段OO1的垂直平分线,所以SO1=SO=1。故选C。
评注 解决球与其他几何多面体间的“接”的问题,关键在于仔细观察和分析,弄清相关元素的几何关系和数量关系,选准最佳角度作出截面,使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系,达到空间问题平面化的目的。
例7 正四面体的内切球、与棱相切的球、外接球这三类球的半径之比为。
解析 设正四体的棱长为1,外接球和内切球半径依次为R、r,由正四面体三个球心重合及其特征,则正四面体的高
评注 正四面体的棱长为a,高为h,外接球、内切球的半径分别为R、r,相邻两个表面所成的角为θ,则,其推导方法中隐含着等体积变换和分割法。如果将正四面体纳入正方体中得到其伴随正方体,正四面体的体积等于其伴随正方体体积的,正四面体的外接球和其伴随正方体的外接球是同一个球,正四面体的棱长等于其伴随正方体棱长的倍。利用这种伴随关系可以简化求正四面体的有关问题。
例8 设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )。

解析 过三棱柱的侧棱AD及球心O作一平面截球,得如图所示的平面,设点G为正三角形ABC的中心,连接AO、OG,则OG⊥AG,


四、考查与多球有关的接、切
策略解决此类问题的关键是抓住球与球之间的连心线的长是两球半径的和。
例9 将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为( )。

解析 由题意,四个半径为1的小球的球心O1,O2,O3,O4恰好构成一个棱长为2的正四面体O1-O2O3O4,并且各面与正四面体容器P-ABC的各对应面的距离都为1。

如图所示,正四面体O1-O2O3O4与P-ABC是有共同的外接球球心O的相似正四面体,从而有,
又HQ=1,所以O1P=3,由于

由于“球”是“圆”在空间概念上的延伸,所以研究球的性质时,应注意与圆的性质类比。球的轴截面是大圆,它几乎含有球的全部元素,所以针对有关球的计算,往往可以作出球的一个大圆,化“球”为“圆”来解决问题;在解决与球有关的“切”“接”问题时,一般要过球心及多面体中的特殊点或线作截面,把空间问题转化为平面问题,从而寻找几何体各元素之间的关系。总之,只要发挥好空间想象力,借助于数形结合进行合理转化,所有问题便可迎刃而解。

