活跃节点相关性考虑下的多跳无线网络性能分析

陈 捷，阚保强

（1.湄洲湾职业技术学院自动化工程系，福建莆田 351254；2.南京电讯技术研究所，江苏南京 210007；3.空军工程大学防空反导学院，陕西西安 710051）

为了分析网络的平均吞吐量，首先分析一下节点的占用率问题.由式（1）可知，在随机信道接入概率下，节点的占用率为

活跃节点相关性考虑下的多跳无线网络性能分析

陈 捷1，2，阚保强2，3

（1.湄洲湾职业技术学院自动化工程系，福建莆田 351254；2.南京电讯技术研究所，江苏南京 210007；3.空军工程大学防空反导学院，陕西西安 710051）

对于无线网络性能分析的研究多是采取信息论和排队论的方法，这些方法虽然可以较好得对点到多点的无线网络进行建模分析，但是对于多跳无线网络（MHWN），由于其固有的分布式及相关性特点，已有方法存在建模复杂和可扩展性差等问题.为了更好的反映多跳网络中的活跃节点相关性特点，提出了一种结合随机几何理论和统计物理学理论的分析方法.数值分析结果表明，本文的模型不仅易于建模和分析，也更加准确和具有可扩展性.

多跳无线传感网络；相关性；随机几何；统计物理学

0　引言

随着无线网络技术的发展，以多跳为架构的网络不断涌现，比如WSN、VANET、Mesh网、多跳微蜂窝网等.多跳无线网络之所以得到广泛的应用，主要是相比于传统蜂窝网络和WLAN具有：易于快速部署，可重构，容错性强等特点.正是由于多跳网络这些特点，也使得对其网络性能建模，相比于传统网络更加困难.目前，对于多跳无线网络的网络性能建模多是基于信息论和排队论.信息论对于传统的点到点的性能分析已经非常成熟［1］，但是对于多跳下的网络性能分析则显得非常困难，这主要是传统信息论无法对节点间活跃相关性进行准确描述，因为在多跳无线网络中，每个链路都是随着时间变化的.同时，在多跳网络中，由于可能存在多条数据流，流间的相互作用对于网络的端到端延时及吞吐量也是非常重要的，当网络规模较小时用排队论进行分析也许可行［2-6］，但随着网络规模的不断增加，排队论的方法将很难进行分析.由此可以看出，对于多跳无线网络的性能分析，必须采取综合考虑网络链路动态变化特性的方法.

对于无线网络下的点到点链路性能分析一直是无线网络领域的一个研究重点［7-13］.基于以上考虑，本文提出了一种结合随机几何理论和统计物理学理论的分析方法.首先给出针对多跳无线网络性能分析的国内外相关典型研究方法；接着对网络模型进行了分析研究，并给出了与统计物理学理论的关系；采取统计物理学理论对多跳无线网络的吞吐量和延时性能进行了理论分析；最后给出了数值分析结果并与实验仿真结果进行了对比.

1　系统模型

1.1网络模型

对于多跳无线网络，其典型的拓扑结构如图1（a）所示，这里以一个数据流（flow）为例.源节点S以固定速率产生定长的包，并通过中继节点1-N传输到目的节点D.为了便于分析，假设中继节点间距是等长的，并且设网络是以时槽工作的，即传输发起均在槽边界发生，时槽的宽度设为恰好完成一个包的传输.

图1　多跳无线网络数据流模型及其基于时槽的随机接入工作过程

同时，对于网络的排队假设都在源节点处，其余中继节点对于每一个数据流只存在单位缓存长度，也就是说中继节点最多拥有一个包.对于传输过程，对当前中继节点有包时其不能接收传输，上一节点通过不断不限次数的重传实现包的成功传输.也就是说当源节点有包待传和目的节点处于队列空状态时，才会成功地完成一次包传输过程，由于不限次数，理论上来说，包的传输最终会成功.

为了便于分析，寻址方式采取基于时槽随机接入的方法，即节点在每个时槽以概率q接入信道发起传输［9，10］.图1（b）给出了基于时槽的共享信道下的多跳传输过程.

1.2统计物理学排他过程模型

为了更直观地考察多跳无线网络流模型与统计物理学排他过程的关系，这里首先简要介绍以下排他过程模型.

统计物理学排他过程模型最早由Macdonald J T和Gibbs J H提出，用以模拟高分子聚合物的动力学原理，并且成功解释了核糖体在细胞中的运动情况，虽然排他过程模型只是一种简单的具有排斥作用的一维格子气系统，但它具有很多独特的特性：如自发性对称性破缺，由边界条件导致的相变及缺陷导致的相变.在排他过程模型中，若粒子仅向一个方向跳转，则该模型变为完全非对称简单排他过程.近年来，这些模型吸引了人们的注意，被广泛应用于分析动态系统中.

一个典型的开放边界一维排他过程如下：假设一个系统有N+1个点（site），编号为0到N，点0作为源被注入粒子，开放边界的意思是粒子在系统的点1被注入，在点N离开.在时刻t对于点i（1≤i≤N）的配置定义为或简记为，其取值为，也就是在每个状态，点要么被占用，即τi［t］=1，要么是空的，即τi［t］=0，而对于源点0则一直处于被占用状态，即任意t＞0，τ0［t］≡1，同时在初始时刻，所有其他点都是空的，即τi［0］=0，0＜i≤N.

在离散时间条件下，则是在时槽（slot）t选择配置（τ1［t］，τ2［t］，…，τN［t］）∈｛0，1｝N，在下一个时槽t+1，则基于采用的何种更新过程来完成配置.即如果粒子在site i的下一个点i+1处于空状态，则粒子以一定概率跳跃到site i+1，以此类推，直到出口点.这个过程类似于空洞的迁移过程，其具体演化过程如下：

当1＜i≤N-1，如果点i+1处于空态，则粒子在点i处以概率p跳跃到i+1，即在时槽t+1，点i为空态的概率为（1-τi［t］（1-p+pτi+1［t］）），点i+1被占用的概率为pτi［t］+τi+1［t］（1-pτi［t］）.

对于点i=1，如果在t时处于被占用状态，则t+1时则仍被占用，而如果处于空态则被占用的概率为αp，即P（τ1［t+1］=1）=αp+（1-αp）τ1［t］.

对于点N，如果其在t时处于空态，则t+1时则仍处于空态，而如果处于被占用则t+1时被占用的概率为βp，即P（τN［t+1］=1）=（1-βp）τN［t］.

参数α，β，p分别是入率（influx rate）、出率（outflux rate）及跳跃概率.图2给出了完全非对称简单排他过程的基本模型图.可以看出，只有（τi［t］，τi+1［t］）配置为（1，0）时，粒子才从site i以概率p发起跳跃.

图2　统计物理学一维排他过程模型

前面提到的几个参数的取值，是依赖于排他过程的更新规则的，即粒子空时跳跃、注入以及移除顺序.对于排他过程一般有4种基本的更新过程：1）随机序列更新：即在每个slot以概率1/（N+1）选择site，粒子在i=0，i=N和0＜i＜N的跳跃概率分别为αp，βp和p；2）成对并行更新：即采取成对的方式进行，首先在site 0/N执行注入/移除，接着在（2，3），（4，5）等进行跳转，在下一个时槽则更新（1，2），（3，4）等等；3）按序更新：就是按照出口到入口的顺序依次更新；4）并行更新：就是所有右向site处于空态的粒子同时发起跳转.

从上面的分析不难看出，统计物理学排他过程模型非常类似于多跳网络的数据流过程.site类似于网络中的节点（node），而粒子类似于网络数据流的包，跳跃概率p类似于包传输成功率，而排他过程的空洞迁移模型类似于单位队列的变化过程.如果配置τ0［t］=1，∀t，即源节点处于饱和状态，则引入排他过程模型的网络流模型可描述成如图3所示.中继节点活跃相关性特征完全可以用排他过程模型来进行描述.图中p表示跳跃概率，相当于网络链路的连接状态或可用带宽，圆形实体类似于数据包，中继节点均为单元队列长度.

图3　基于统计物理学排他过程对多跳网络建模的等效图

2　基于统计物理学理论的MHWN性能分析

由前面的分析可以看出，基于流的多跳无线网络过程与统计物理学中的排他过程模型非常类似.为了便于分析，首先采用单数据流下的网络模型为例进行分析，随后分析多数据流下的网络性能.

2.1单数据流下的网络性能分析

在单数据流网络中，一般包括源节点S、目标节点D和中继节点，假设跳数为N，如图1（a）所示.假设网络源节点处于饱和状态，则网络将在α=β=1时处于最大服务状态.同时，假设相邻中继节点的距离均为d，则在大尺度衰落条件下，链路信道传输成功率为ps=Pr［SNR＞θ］=exp（-θN0dγ），其中θ是最小信干比要求阈值，γ是路径衰落指数，N0是接收带宽噪声.

1）吞吐量分析

首先分析稳态占用率.由于采取时槽随机接入控制机制，则可基于并行更新的排他过程模型进行分析.由文［11］知，对于并行更新的排他过程，其稳态占用率为：

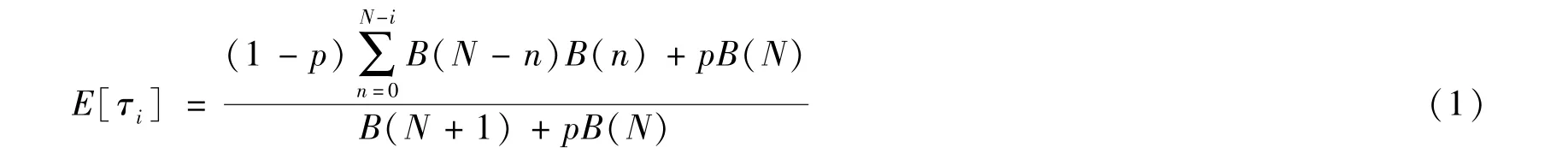
其中，p是基于并行更新的排他过程的粒子跳转概率，图4给出了稳态占用率与参数p的关系.基于单数据流的网络模型，对于网络链路来说，设其平均成功率为ps，则结合节点信道接入概率q，则可得p=

基于以上稳态占用率分析，可得到以下定理.

定理1 对于类似与拓扑1的网络，在基于时槽随机接入概率q机制下，网络稳态吞吐量为

证明 在任意时槽，节点N有包的概率为E［τN］，由其发起传输的概率为q，链路成功率为ps，则网络的吞吐量为S=qpsE［τN］，基于式（1）代入后化简可得式（2）.证毕.

2）网络平均延时分析

对于单数据流网络，节点i遍历的平均数据包个数为E［τi］，所以由Little理论可得包在节点i的平均延时为E［τi］/S.即E［Di］=E［τi］/（qpsE［τN］），0≤i≤N.

则可得网络的平均端到端延时为：

2.2多数据流下的多跳无线网络性能分析

在多条数据流下，网络的业务可以分解为多个多跳数据流.假设源节点服从密度为δ的PPP（Poisson point process）分布，其余节点服从密度为1-δ的PPP分布，这样网络节点的总密度为1.网络的路由策略选择基于方向和位置的逐跳路由策略.如图5所示，即节点的下一跳选择是基于方位角φ区域内的最近的第n个节点.比如图5所示，取n=1，则i节点则选择在φ区域内距离最近的第一个节点i+1作为下一跳，然后节点i+1以同样的方法在其与目的节点形成的φ区域内，选择距离最近的第一个节点i+2作为下一跳，以此类推.图6给出了一个基于该路由策略形成的路由拓扑图.

图4　稳态占用率与参数p的关系

图5　逐跳最近n节点路由算法示意图（n=1）

图6　路由拓扑图（φ=0.05，n=1）

接下来，基于随机几何理论和排他过程模型分析多数据流下的网络平均吞吐量和延时性能.通过对网络性能的分析，可以对如何优化网络设计提供参考，比如对于源节点密度的优化、路由跳数的优化、空间吞吐量最大化等.

由随机几何理论知，对于密度为λ的PPP网络，任意节点夹角为φ的区域内，与其最近的第n个节点相距该节点为Rn的分布函数概率密度为

由上式可得

为了分析网络的平均吞吐量，首先分析一下节点的占用率问题.由式（1）可知，在随机信道接入概率下，节点的占用率为

其中，q是节点的信道接入概率，ps是链路信道成功传输率.

对于链路信道成功传输率ps，涉及到多流下的链路相互间干扰，由前文假设可知，稳态时，对于每个数据流，如果有N个中继的话，平均数据包数为（1+N/2）.由源节点的密度为δ，则在随机信道接入下干扰源的密度最大为δq（1+N/2）.尽管每个流的发起是不一致的，为了从平均意义上分析，这里可以认为干扰节点服从密度为δq（1+N/2）的PPP分布.则可以得到以下定理.

定理2 对于上述描述的基于时槽随机接入的多数据流网络，如果采取基于最近第n个邻居的路由策略，其链路的平均成功率为其中，φ是方向角，λ≤δq（1+N/2）是干扰I节点密度，c=πΓ（1+2/γ）Γ（1-2/γ）θ2/γ.

证明 由干扰节点密度为λI，则基于文［2］，可知对于Poisson网络中距离为r的链路信道成功率为ps（r）=exp（-λIcr2），其中，c=πΓ（1+2/γ）Γ（1-2/γ）θ2/γ，由前面假设知，中继节点密度为1-δ，则令λ=1-δ，带入式（4），结合式（6）可得基于最近第n个节点传输链路成功传输率为

同样基于Little理论可以得到稳态下的典型数据流的端到端延时为：

由于是多数据流的网络，这里有必要分析以下网络吞吐量密度，吞吐量密度是指单位面积内网络成功传输的平均包数.由以上各式，考虑到干扰源密度选取的为上界，可得网络吞吐量密度的下界为：

由上式可以看出，通过调整δ或n可以使得网络吞吐量密度最优.

3　仿真分析

3.1仿真环境

将节点以密度为1的PPP分布部署在50×50的区域内，则在网络中平均有2 500个节点.取源节点密度为δ=0.01，SIR阈值θ设为10 dB，路由方向角φ取值为π/2，路径衰落系数γ设为4.为了避免边界问题带来的影响，在结果分析中，只对40×40区域内的数据流进行统计分析，时槽选取3 000～5 000之间，以更准确得反映网络平均性能.

3.2仿真结果

图7给出了N=4时，网络稳态吞吐量密度的示意图.可以看出，数值分析结果与实验结果非常接近（这里的试验结果是基于蒙塔卡洛模拟的结果），基本验证了本文所采取方法的准确性.

为了分析网络吞吐量与延时的折中问题，给出了D（N）/S（N）与ps、N的关系曲线，如图8所示，同时给出了D（N）、S（N）随着链路质量的变化曲线，如图9所示.可以看出，在一定的链路质量条件下，可以通过优化跳数实现一定延时要求下的吞吐量最优.

图7　网络稳态吞吐量密度数值分析结果与实验结果比较图（N=4，φ=π/2）

图8　网络性能与中继节点数N的关系图（R=1，q=0.2）

图9　网络性能与ps的关系图（R=1，q=0.2）

4　结论

针对多跳无线网络性能建模进行了研究，通过引入统计物理学排他过程模型，对多跳无线网络节点的活跃相关性进行了很好的描述，并结合随机几何理论对链路干扰对网络性能的影响进行了建模.数值仿真结果表明本文的方法不仅准确度较高，而且具有较好的可扩展性，通过模型还对网络的参数优化设置进行了研究.在以后的工作中，将围绕基于本文模型进行路由优化并开展相关研究工作.

［1］ Cover T，Gamal A E.Capacity theorems for the relay channel［J］.IEEE Transactions on Information Theory，1979，25（5）：572-584.

［2］ Andrews J G，Jindal N，Haenggi M，et al.Rethinking information theory for mobile ad hoc networks［J］.IEEE Communications Magazine，2008，46（12）：94-101.

［3］ Song G Z，Yang L，Wu J，et al.Performance comparisons between cellular-only and cellular/WLAN integrated systems based on analytical models［J］.Frontiers of Computer Science in China，2013，7（4）：486-495.

［4］ Cecilia A C，Solon V Carvalho.An analytical framework for distributed coordinated scheduling in IEEE 802.16 wireless mesh networks［J］.Ad Hoc Networks，2014，13：181-190.

［5］ 刘沼辛，高春雪.基于冲突感知的IEEE802.11DCF性能分析模型［J］.燕山大学学报，2013，37（2）：148-152.

［6］ 阚保强，范建华，王建业，等.认知无线网络信道接入协议［J］.软件学报，2012，23（7）：1824-1837.

［7］ Alamino R C，Saad D.Statistical mechanics analysis of LDPC coding in MIMO Gaussian channels［J］.Journal of Physics A：Mathematical and Theoretical，2007，40（41）：12259-12279.

［8］ Kramer G，Gastpar M，Gupta P.Cooperative strategies and capacity theorems for relay networks［J］.IEEE Transactions on Information Theory，2005，51（9）：3037-3063.

［9］ Goldsmith A，Wicker S B.Design challenges for energy-constrained ad hoc wireless networks［J］.IEEE Wireless Communications Magazine，2002，9（4）：.8-27.

［10］ Takeuchi K，Tanaka T.Statistical-mechanics-based analysis of multiuser MIMO channels with linear dispersion codes［J］.Journal of Physics：Conference Series，2008，95（1）：22-26.

［11］ Srinivasa S.Haenggi M.Combining stochastic geometry and statistical mechanics for the analysis and design of mesh networks［M］.Newyork：Elsevier Ad Hoc Networks，2011.

［12］ Evans M R，Rajewsky N，Speer E R.Exact solution of a cellular automaton for traffic［J］.Journal of Statistical Physics，1999，95（1）：45-96.

［13］ Srinivasa S，Haenggi M.The TASEP：A Statistical Mechanics Tool to Study the Performance of Wireless Line Networks［M］.//Proc.Int’l Conf.Computer Comm.and Networks，2010：1-8.

［14］ Scutari G，Facchinei F，Song P，et al.Decomposition by partial linearization：Parallel optimization of multi-agent systems［J］.IEEE Trans Signal Process，2014，62（3）：641-656.

Performance Analysis for MHWN Considering Correlation Among Active Nodes

CHEN Jie1，2，KAN Bao-qiang2，3
（1.Department of Automation Engineering，Meizhouwan Vocational Technology College，Putian Fujian 351254，China）（2.Nanjing Telecommunication Technology Research Institute of CESEC，Nanjing Jiangsu 210007，China）（3.Missile College of Airforce Engineering University，Xian Shanxi 710051，China）

In recent years，classical information theory and Queuing theory have been successfully studying point-to-multipoint links in wireless network.However，they are not enough to characterize the intricacies of multihop wireless networks（MHWN）for inherent interactions between nodes.In this paper，we focus on the modeling and analysis of multihop wireless networks.To make the model present strong correlations inter-dependencies between the active nodes in MHWN，we use exiting theory from stochastic geometry and statistical physics to analyze performance for MHWN.Numerical results show that our model can allow a clean，yet accurate analysis，and provide scalability with nodes in the network.

multihop wireless sensor networks；correlation；stochastic geometry；statistical physics

TP392

A

1671-6876（2016）03-0221-07

［责任编辑：蒋海龙］

2016-06-08

国家自然科学基金资助项目（61201216）；福建省中青年教师教育科研项目（JA15855）

阚保强（1980-），男，山东鱼台人，高级工程师，博士，主要研究方向为无线网络.E-mail：bqkan@163.com