情报数据驱动的在线仿真系统动态修正方法

焦　松，李　伟，楚　威，毛少杰

（1.中国电子科技集团公司第二十八研究所信息系统工程重点实验室，江苏　南京 210000；

2.哈尔滨工业大学控制与仿真中心，黑龙江　哈尔滨 150001）

情报数据驱动的在线仿真系统动态修正方法

焦松1，李伟2，楚威1，毛少杰1

（1.中国电子科技集团公司第二十八研究所信息系统工程重点实验室，江苏南京 210000；

2.哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨 150001）

为了保证面向指挥决策支持的在线仿真系统可信性，提出了情报数据驱动的在线仿真系统动态修正方法。首先，依据情报数据变化快慢，将其分为缓变和快变两类数据；然后，从位置接近性和外形相似性两个方面刻画缓变数据间差异，从趋势项差异和平稳项差异两个方面刻画快变数据间差异，由此实现了仿真输出与情报数据一致性的度量；进一步，基于拉丁超立方实验设计方法确定仿真模型“修正集合”，并利用主成分分析综合仿真输出一致性指标，从修正集合中选择使得仿真模型可信性最佳的修正方案。通过应用实例，表明了方法的有效性。

在线仿真；动态修正；仿真输出一致性；主成分分析

网址：www.sys-ele.com

0　引　言

随着军事技术的不断发展，战场环境日益复杂，作战方式将由按预案行动转变为根据战场态势临机调整行动。此时，如何辅助指挥员实现快速、准确的决策，对获取信息优势和决策优势，取得战场主动权起着决定性作用。

仿真具有安全、高效且能模拟多种战情等特点，由此成为了一种支持指挥决策的重要手段。美国海军制定的嵌入式仿真基础设施（embedded simulation infrastructure，ESI）计划、美国空军围绕实时行动方案分析相继开展的一系列研究以及美国国防部高级研究计划署（DARPA）提出了“深绿”计划［13］，目的均是将仿真嵌入实际指挥控制系统中，通过在线的作战方案仿真评估，为指挥员提供更为精确的战场态势和行动建议。“在线仿真”是上述应用的核心技术，与“动态数据驱动应用系统”（dynamic data driven application system，DDDAS）、“共生仿真”以及“嵌入式/平行仿真”具有相似的技术内涵［46］，均是通过对真实系统全局或局部进行实时、在线的交互式仿真，生成关键数据，为真实系统的运行、控制、决策等提供支撑。

对于面向指挥决策支持的在线仿真系统而言，如何依据实时的情报数据动态修正仿真系统，进而确保仿真系统的可信性，是一个亟需解决的关键问题。早在1967年，Naylor和Finger就开始研究了仿真模型可信性问题，指出可依据领域经验知识对仿真模型进行表面验证，还可以从典型事件以及系统特征等多种视角分析仿真模型与真实对象间的一致性［7］。至今，已形成较为丰富的仿真模型可信性评估方法，例如：Theil不等式系数（Theil inequality coefficient，TIC）、灰色关联分析以及误差分析等时域分析方法［810］，窗谱、最大熵谱和交叉谱等频域分析方法［1112］。当仿真输出为单输出且仿真模型仅存在有限种修正可能时，上述方法能较为有效地从有限种修正方案中选出最佳者。此外，文献［13-14］以仿真模型可信度为目标，通过优化指导仿真模型的修正。但是，文献［13］中基于贝叶斯的修正方法使用条件较为苛刻，且计算量大；文献［14］直接在仿真模型上开展可信度的优化工作，执行效率也较为低下。由上可知，已有方法未能很好地解决仿真输出为多变量输出的仿真模型修正问题。

为了解决面向指挥决策支持的在线仿真系统存在多变量输出时的动态修正问题，本文首先给出了仿真输出一致性度量模型，然后构建仿真模型的修正集合，进一步综合仿真输出一致性评估指标，从修正集合中选出使得仿真模型可信性最佳的修正方案。

1　问题描述及分析

用R和S分别表示战场目标及其仿真模型。用Yr=｛yr1，yr2，…，yrm｝和Ys=｛ys1，ys2，…，ysm｝分别表示战场目标情报及其仿真模型输出，其中yri和ysi（i=1，2，…，m）分别表示Yr和Ys的第i个输出量。

用C（Ys，Yr）表示Ys相对于Yr的一致性程度，简称仿真输出一致性，且C（Ys，Yr）∈（0，1］。图1示意性给出了Ys和Yr之间的差异与C（Ys，Yr）的关系。当Ys与Yr完全一致时，即二者没有差异时，可认为仿真模型完全可信，则有C（Ys，Yr）=1；当Ys相对于Yr一致性程度越差，即二者差异趋于无穷大时，可认为仿真模型越不可信，则有C（Ys，Yr）→0。

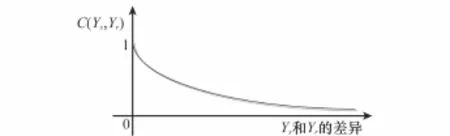
图1　Ys和Yr之间的差异与C（Ys，Yr）的关系

用Vi或Vi（ysi，yri）（i=1，2，…，m）表示yri相对于ysi的符合程度，简称仿真输出符合度，且Vi（ysi，yri）∈（0，1］。当yri与ysi完全吻合时，则有Vi（ysi，yri）=1；当yri与ysi越不吻合时，则有Vi（yis，yir）→0。

用Eij或Eij（ysi，yri）（i=1，2，…，m；j=1，2，…，ni）表示仿真输出符合度Vi的度量指标，且定义如下：

式中，Fi（·）为仿真输出符合度度量指标综合模型；G（·）为仿真输出符合度综合模型。

用ai（i=1，2，…，k）表示作战实体仿真模型S可调整的参数或者规则，其取值集合为Ti，则目标情报流驱动的在线仿真系统动态修正问题可被描述为如下的优化问题：

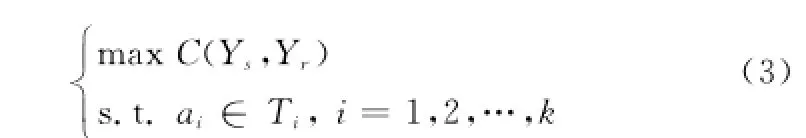
如果基于上述三式来解决在线仿真系统的动态修正问题，则存在两个难点：①当系统存在多个输出，且仿真输出符合度需要多个指标度量时，难以确定Fi（·）和G（·），由此也难以得到C（Ys，Yr）；②基于式（3）的仿真优化工作一般时耗较大，可能难以满足在线仿真的时效性要求。针对上述难点，本文给出了如下研究思路：

（1）为了提高修正效率，以牺牲修正精度为代价，将仿真模型的“优化”问题转变为仿真模型的“优选”问题，即仅从取值集合Ti中选取出有限个可选项构造修正集合Ai；

（2）将C（Ys，Yr）的“价值评估”问题转变为“排序评估”问题，由此避免了确定Fi（·）和G（·），而只需确定有限个可选项对应C（Ys，Yr）的大小排序关系。

2仿真输出一致性度量方法

假定y=＜y（1），y（2），…，y（N）＞为一个时间序列，其中y（i）（i=1，2，…，N）为按时间先后依次观察得到的数据，对应的观测时刻用t（i）（i=1，2，…，N）表示，且假定t（1）=0。由此定义y=＜y（1），y（2），…，y（N）＞随时间的变化频率为

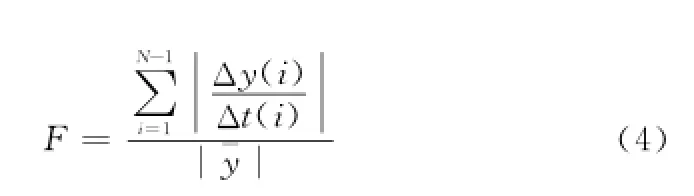
由此，假定f0≥0为评定数据变化快慢的临界值，可以由专家依据具体的领域设定。如果F≥f0，则认为y=＜y（1），y（2），…，y（N）＞为快变数据；否则认为y=＜y（1），y（2），…，y（N）＞为缓变数据。

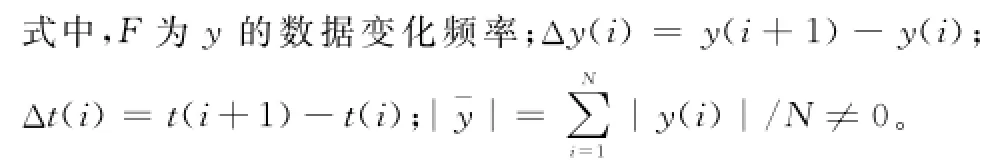
2.1缓变数据特征差异度量模型

假定情报数据yr和仿真输出ys为缓变数据，分别由相应的系统运行P次和Q次后，对多次运行输出在每个采样点进行平均处理后，得到的情报数据和仿真输出如下：

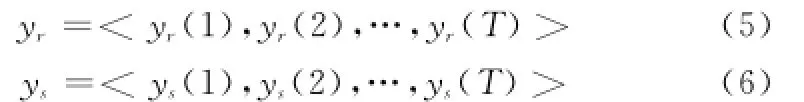
在此，令Z=＜z（1），z（2），…，z（T）＞=＜ys（1）-yr（1），ys（2）-yr（2），…，ys（T）-yr（T）＞，如果z（1），z（2），…，z（T）彼此间相差不大，则表明ys与yr的外形较相似，特别当ys与yr重合或平行时，有z（1）=z（2）=…=z（T）；如果z（1），z（2），…，z（T）彼此间相差较大，则表明ys与yr外形的相似性较差。从位置差异es和外形差异et两方面刻画yr与yr之间的差异，定义如下：

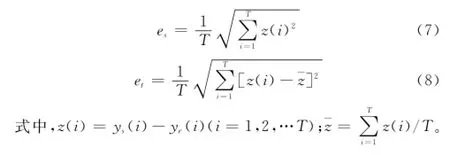
2.2快变数据特征差异度量模型

假定情报数据yr和仿真输出ys为速变数据，与缓变数据处理方式相同，得到：

由于快变数据一方面包含反映波动特征的平稳项，另一方面包含反映数据整体变化趋势特征的趋势项。基于经验模态分解算法可将二者分离，具体算法见文献［15］。由此给出如下定义：

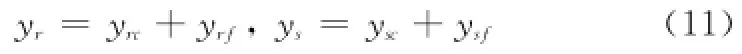
式中，yrc和ysc分别为yr和ys的趋势项；yrf和ysf分别为yr和ys的平稳项。

yrc和ysc为缓变数据，可以直接依据式（7）和式（8）计算es和et来刻画二者的差异。yrf和ysf可以通过窗谱分析转换至频域中得到各自的谱密度，进而通过谱密度差异刻画yrf和ysf之间的差异，具体原理见文献［11］，由此定义如下：

式中，ef表示yrf和ysf的谱密度差异；M 表示yrf和ysf转换至频域中的点数；m表示通过相容性检验的点数。

3　在线仿真系统动态修正方法

在仿真输出一致性度量的基础上，给出本文的在线仿真动态修正方法如下：

步骤1以作战实体仿真模型S的可调整参数和规则ai∈Ti（i=1，2，…，k）为试验因子，采用拉丁超立方方法确定修正集合K=｛A1，A2，…，Ap｝；

步骤2得到修正集合中每个元素对应的仿真模型输出Ysi（i=1，2，…，p），并采用上述度量方法得到Ysi与Yr之间的一致性度量指标值eij（i=1，2，…，p；j=1，2，…，q）；

步骤3由于ei1，ei2，…，eiq之间可能存在着较强的相关性，采用主成分分析方法进行处理，得到相互独立的若干主成分以及对应的贡献率ηi1， ηi2，…，ηil；

步骤4以ηi1，ηi2，…，ηil的大小表征的重要程度，进行归一化处理得到权重为ωi1，ωi2，…，ωil，进一步加权求和得到修正集合中每个元素对应的综合评估结果Ei（i=1，2，…，p），其中的最大者对应的仿真模型参数或者规则值即为最终的修正结果。

3.1基于拉丁超立方的修正集确定方法

将作战实体仿真模型S的可调整参数和规则ai∈Ti（i=1，2，…，k）视为实验因子，将Ti（i=1，2，…，k）划分为p个子集合Hji（j=1，2，…，p），使它们满足如下条件：

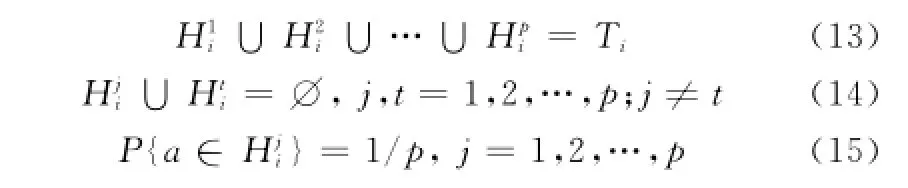
式中，P｛·｝表示事件概率。

基于拉丁超立方试验设计方法，具体算法内容参见文献［16］，生成一个p×k的拉丁超立方矩阵U，使得U中的每列均为1，2，…，p的一个随机全排列。令bij∈｛1，2，…，k｝（i=1，2，…，p；j=1，2，…，k）为U中第i行j列的取值，由此得到修正选项为

式中，Ai（i=1，2，…，p）为第i个修正选项；a（j=1，2，…，k）为aj在集合上的取值。

3.2基于PCA的修正方案优选方法

运行仿真系统，得到修正选项Ai（i=1，2，…，p）对应的仿真模型输出Ysi（i=1，2，…，p）。采用上述仿真输出一致性度量方法得到Ysi与情报数据Yr之间的一致性度量指标值eij（i=1，2，…，p；j=1，2，…，q）。

由于eij（i=1，2，…，p；j=1，2，…，q）之间存在相关性，即它们所蕴含的信息存在一定的“重叠”。在此，采用主成分分析法从q个数据差异中提取少数几个相互独立且包含了大部分信息的主成分，具体算法原理参见文献［17］。

首先对ei1，ei2，…，eiq（i=1，2，…，p）进行标准化处理如下：

进一步，构造协方差阵为

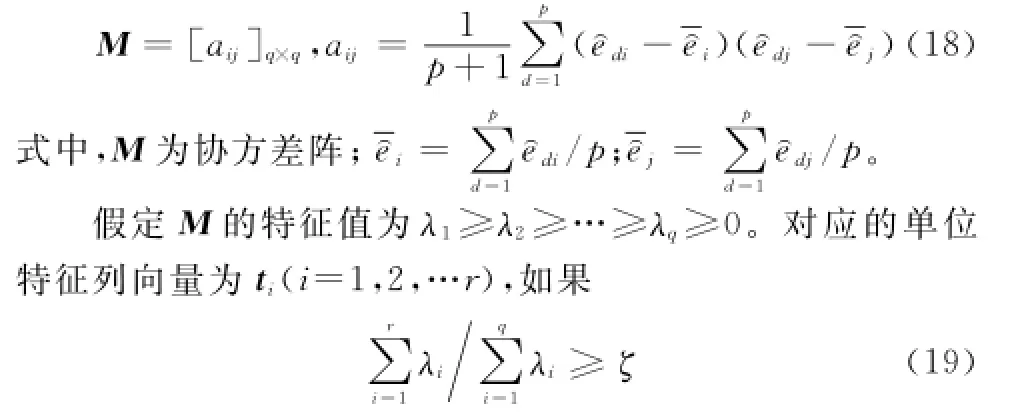
式中，ζ∈［0，1］为主成分判定阈值。

则经过主成分分析后得到新的数据差异为

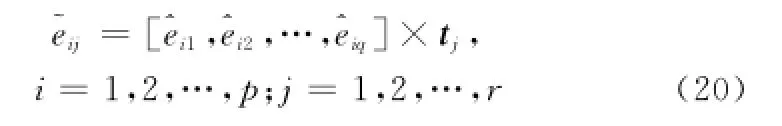
依据每个主成分对区分p个修正选项的贡献率，得到r个主成分的权重为

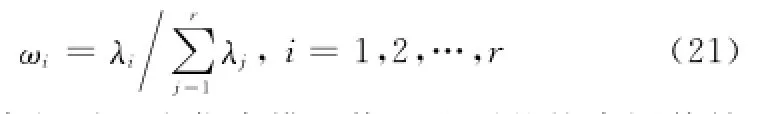
由此，综合得到p个仿真模型修正选项的综合评估结果如下：

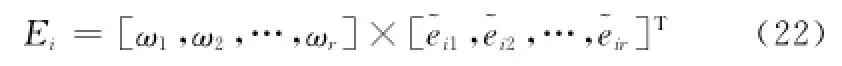
式中，Ei（i=1，2，…，p）为第i个模型对应的综合评估结果。

最后，依据综合评估结果从p个修正备选中选出最佳者，如下：

式中，El所对应的修正选项为最佳者。

4　应用实例

假定我方飞机正遭受敌方地空导弹攻击，如图2所示。M表示敌方导弹；T表示我方飞机；V为敌方导弹速度；VT为我方飞机速度；q为目标线角；η为敌方导弹速度矢量前置角；θ为敌方导弹弹道角，由于攻击平面为铅垂面，所以其也是弹道倾角；ηT为我方飞机速度矢量前置角；σT为我方飞机航向角。

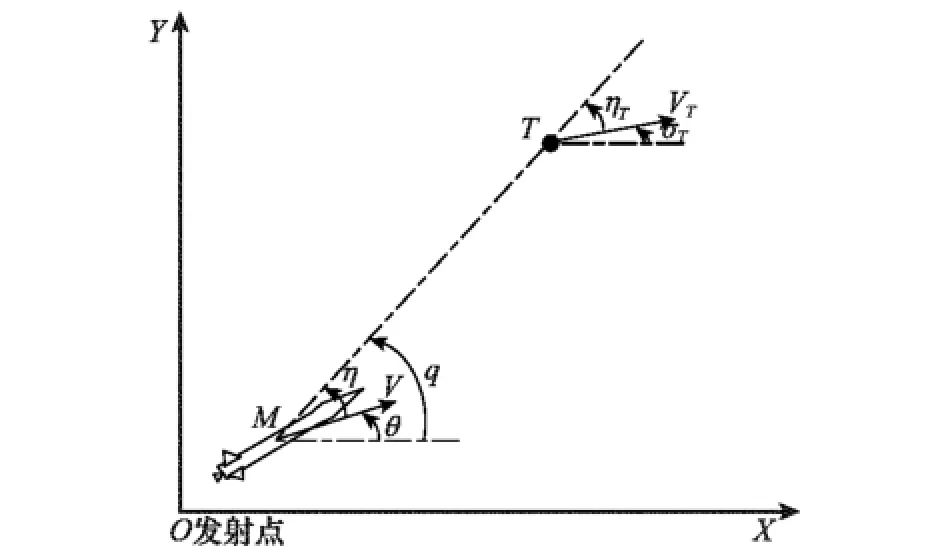
图2　我方飞机与敌方导弹的相对位置

假定现已获取当前12 s内的敌方导弹飞行轨迹数据，如图3所示，并估计得到了导弹的速度以及弹道倾角数据。现拟采用在线仿真的手段辅助我方作战人员制定规避策略，为此需要依据当前12 s内的情报数据，建立较为逼真的敌方地空导弹模型。

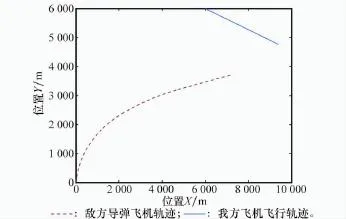
图3　我方飞机和敌方导弹的飞行轨迹

假定依据其他情报信息可知：该敌方导弹采用比例导引进行制导，比例导引律系数K∈［3，8］，导引头惯性环节时间常数Ta∈［0.1，0.6］。由此可知，此时的关键就是利用当前12 s内的情报数据，确定敌方导弹模型的比例导引系统以及导引头惯性环节时间常数。

依据本文方法，将K和Ta视为试验因子，采用拉丁超立方试验设计方法得到的试验点如表1和图4所示。进一步，将每个试验点对应的K和Ta取值代入仿真模型，得到导弹的位置、速度以及弹道角。为了便于清晰显示数据曲线，在此仅给出参考输出和前5组仿真输出，如图5～图8所示。

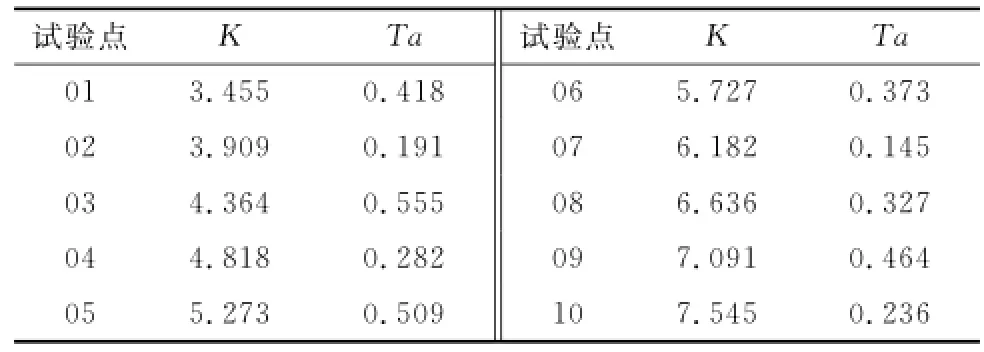
表1　试验点

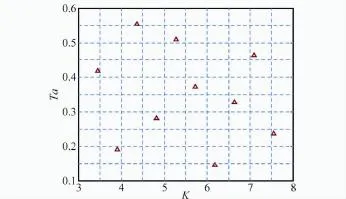
图4　我方飞机和敌方导弹的飞行轨迹

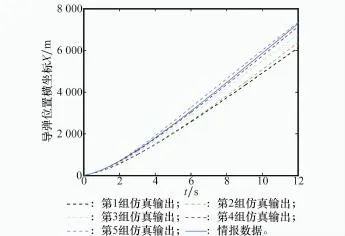
图5　导弹位置X

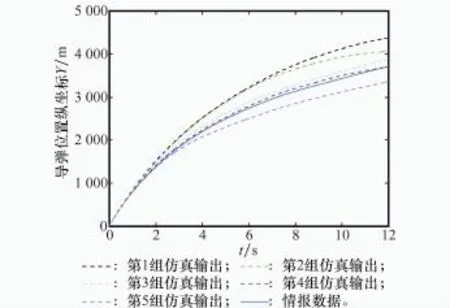
图6　导弹位置Y

图7　导弹速度

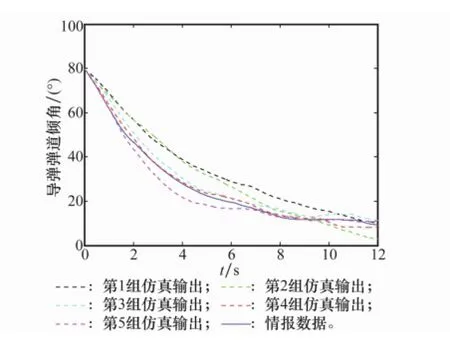
图8　导弹弹道倾角

由于这些数据变化缓慢，可采用式（7）和式（8）得到仿真数据与情报数据之间的差异如表2所示。其中，exs和ext表示位置x对应的仿真数据与情报数据之间的位置差异和外形差异；eys和eyt表示位置y对应的仿真数据与情报数据之间的位置差异和外形差异；eυs和eυt表示速度V对应的仿真数据与情报数据之间的位置差异和外形差异；eθs和eθt表示弹道角θ对应的仿真数据与情报数据之间的位置差异和外形差异。

由上可知，仿真输出与情报数据的一致性可由表2中的8个指标来刻画，由于它们之间存在较强的相关性，经过式（17）的归一化处理得

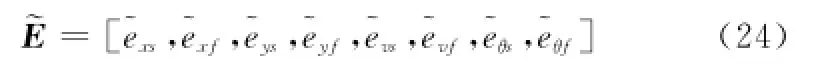
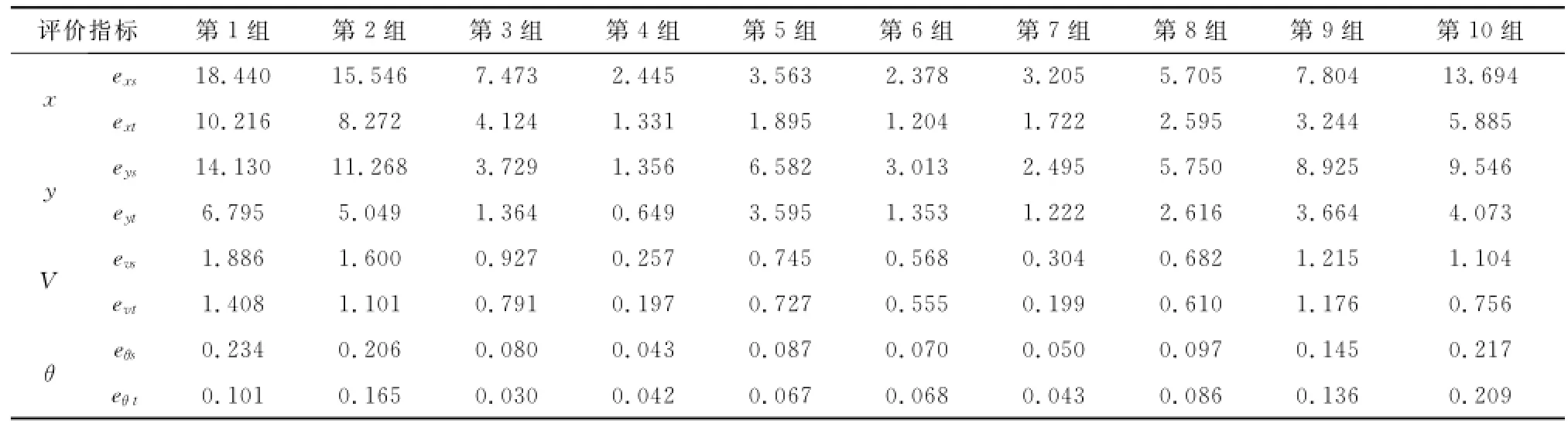
表2　每个试验点对应的仿真输出一致性指标值

进一步通过主成分分析得到各主成分对应的特征值以及对区分10个比较样本的贡献率，如表3和图9所示。

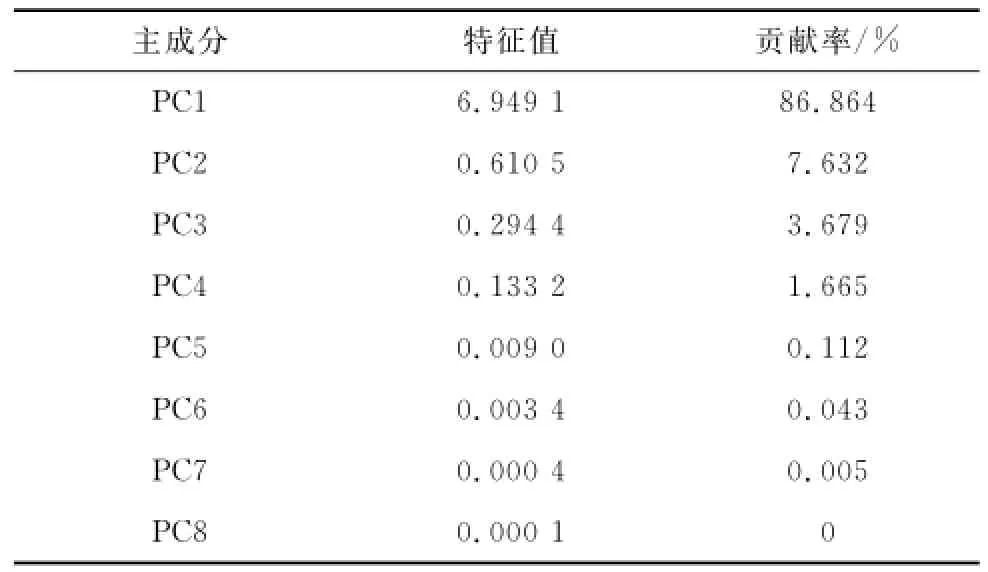
表3　每个主成分对应的特征值和贡献率

令主成分判定阈值ζ=90%，依据式（19），则仅取前2个主成分作为评估指标：

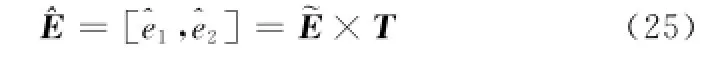
依据前两个主成分的贡献率，由式（21）归一化处理后得到二者的权重分别为0.919和0.081。再依据式（22），得到10组试验点对应的评估结果为4.080 4，3.017 0，-1.088 7，-2.918 1，-0.845 9，-1.956 6，-2.572 4，-0.853 7，1.012 7以及2.125 0。由此可知第4组仿真输出与情报数据差异最小，则将K= 4.818以及Ta=0.282视为最终结果，将第4组仿真输出与情报数据进行比较，如图10～图12所示，二者一致性较好，由此表明修正结果较为合理有效。

图9　前3个主成分的贡献率

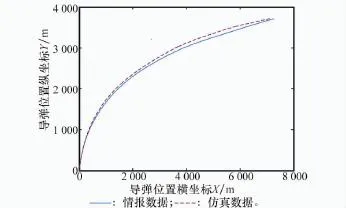
图10　实际位置和修正后的仿真位置

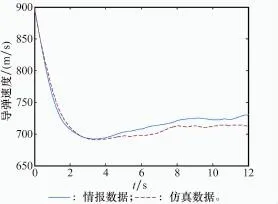
图11　实际速度与修正后的导弹仿真速度

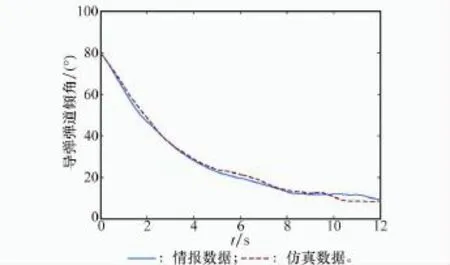
图12　实际弹道倾角与修正后的仿真弹道倾角

5　结　论

利用在线仿真支持指挥决策，前提是保证仿真系统的可信性。实时获取的情报数据是动态修正在线仿真系统的参考依据，本文考虑存在多个修正指标的情形，由此构建了一个多目标优化问题。进一步考虑到该多目标优化方程难以建立，且在线仿真系统存在时效性要求，本文综合利用拉丁超立方试验设计以及主成分分析方法，将上述仿真优化问题转换为排序评估问题予以解决。在应用实例中，基于本文方法有效地利用当前情报数据修正了敌方导弹模型。

［1］Layman G，Daly J.C4I tactical applications utilizing embedded simulations［C］//Proc.of the Command and Control Research and Technology Symposium，2002：1-15.

［2］Gilmour D A，Mc Keever W E.High performance computing（HPC）for real-time course of action（COA）analysis，AFRL-RI-RS-TR-2007 273［R］.Austin：Distribution Unlimited，2008.

［3］Committee on Modeling and Simulation for Defense Transformation，National Research Council.Defense modeling，simulation and analysis-meeting the challenge［R］.Washington，D C：National Academies Press，2006.

［4］Fujimoto R，Lunceford D，Page E，et al.Summary of the parallel/distributed simulation working group［R］.Grand Challenges for Modeling and Simulation，2002.

［5］DDDAS Workshop Report.NSF sponsored workshop on DDDAS-dynamic data driven applications systems［EB/OL］.［2015 05-30］.http://www.cise.nsf.gov/dddas，2006-01-20/2007 09-18.

［6］Hu X F，He X Y，Xu X L.The challenge and thinking of modeling and simulation in the era of big data［J］.China Science：Information Science，2014，44（5）：676-692.（胡晓峰，贺筱媛，徐旭林.大数据时代对建模仿真的挑战与思考［J］.中国科学：信息科学，2014，44（5）：676-692.）

［7］Naylor TH，Finger J M.Verification of computer simulation models［J］.Management Science，1967，14（2）：92-101.

［8］Kheir N A，Holmes WM.On validating simulation models of missile systems［J］.Simulation，1978，30（4）：117-128.

［9］Wu J，Wu X Y，Chen Y X，et al.Validation of simulation models based on improved grey relational analysis［J］.Systems Engineering and Electronics，2010，32（8）：1677-1679.（吴静，吴晓燕，陈永兴，等.基于改进灰色关联分析的仿真模型验证方法［J］.系统工程与电子技术，2010，32（8）：1677-1679.）

［10］Damborg M J.An example of error analysis in dynamic model validation［J］.Simulation，1985，44（6）：301-305.

［11］Liu Z Z.Simulation validation based on the data of the aero experimentation［J］.Journal of System Simulation，2002，14（3）：281-284.（刘藻珍.基于飞行试验数据的仿真模型验证方法的研究［J］.系统仿真学报，2002，14（3）：281-284.）

［12］Jiao S，Li W，Yang M.Validation of simulation models based on

empirical modal decomposition and grey relevance analysis［J］. Systems Engineering and Electronics，2013，35（12）：2613 2618.（焦松，李伟，杨明.基于经验模态分解和灰色关联度分析的仿真模型验证方法［J］.系统工程与电子技术，2013，35（12）：2613-2618.）

［13］Xiong Y，Chen W，Tsui K L，et al.A better understanding ofmodel updating strategies in validating engineering models［J］. Computer Methods in Applied Mechanics and Engineering，2009，198（15）：1327-1337.

［14］Yuan J，Ng S H，Tsui K L.Calibration of stochastic computer models using stochastic approximation methods［J］.IEEE Trans. on Automation Science and Engineering，2013，10（1）：171-186.

［15］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society Mathematical Physical&Engineering Sciences，1998，454：903-995.

［16］Minasny B，McBratney A B.A conditioned Latin hypercube method for sampling in the presence of ancillary information［J］.Computers &Geosciences，2006，32（9）：1378-1388.

［17］Huo DH，Yang D，Zhang XH，et al.Principal component analysis based Codebook back-ground modeling algorithm［J］. Acta Automatica Sinica，2012，38（4）：591-600.（霍东海，杨丹，张小洪，等.一种基于主成分分析的Codebook背景建模算法［J］.自动化学报，2012，38（4）：591-600.）

Dynamic modification of online simulation system based on intelligence data-driven

JIAO Song1，LI Wei2，CHUWei1，MAO Shao-jie1
（1.Science and Technology on Information Systems Engineering Laboratory，The 28th Research
Institute of China Electronics Technology Group Corporation，Nanjing 210000，China；2.Control and Simulation Center，Harbin Institute of Technology，Harbin 150001，China）

To ensure the creditability of the online simulation system for decision-making，the method for dynamically modifying the online simulation based on intelligence data-driven is proposed.The intelligence data are divided into gradual data and fast data according to the change ratio.For describing the consistency between the simulation output and the intelligence data，the differences between the gradual data are depicted by the proximity of the position and the similarity of the shape，the fast data is decomposed into the trend item and stationary item，and the measure models of differences for each item are given.Furthermore，the modification set of the simulation model is gained via Latin hypercube sampling，the best modification scheme is selected by integrating the consistency indexes of the simulation output based on principal component analysis.Finally，the validity of the method is shown in the application.

online simulation；dynamic modification；consistency of simulation output；principal component analysis

TP 391.9

A

10.3969/j.issn.1001-506X.2016.05.35

1001-506X（2016）05-1201-07

2015-06-04；

2015-11-17；网络优先出版日期：2015-12-14。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151214.1349.008.html

国家自然科学基金（61403097）资助课题

焦松（1985-），男，工程师，博士，主要研究方向为仿真试验评估。

E-mail：jiaosong1985@163.com

李伟（1980-），男，副教授，博士，主要研究方向为仿真实验设计与分析、分布式仿真。

E-mail：fleehit@163.com

楚威（1979-），男，高级工程师，主要研究方向为综合电子信息系统建模与仿真。

E-mail：wicked@163.com

毛少杰（1963-），男，研究员，主要研究方向为综合电子信息系统建模与仿真。

E-mail：maoshojie@163.com