基于私有云和改进粒子群算法的约束优化求解

张永强，徐　宗昌，呼凯凯，胡春阳

（1.装甲兵工程学院技术保障工程系，北京 100072；2.海军航空兵学院，辽宁　葫芦岛 125000）

基于私有云和改进粒子群算法的约束优化求解

张永强1，2，徐宗昌1，呼凯凯1，胡春阳1

（1.装甲兵工程学院技术保障工程系，北京 100072；2.海军航空兵学院，辽宁葫芦岛 125000）

为提高约束优化模型的求解准确度和运算速度，针对粒子群算法及其计算方法进行了改进。引入多样化机制避免算法陷入局部最优的危险：创建多个子群将决策空间划分为多个搜索子空间，多子群独立搜索以保证群间解的多样化；用量子粒子代替普通粒子，为其添加服从球状分布的伴随粒子来提高群内解的多样化。多样化的引入增加了计算量和计算复杂度，利用并行计算提高算法运行速度：分析了改进粒子群算法并行计算的方法，在私有云计算平台上编写了基于Map Reduce的并行求解流程。实验结果表明，本文方法具有较高准确度，算法的稳定性也较好，运算速度可成倍提高。

约束优化；粒子群算法；私有云计算平台；并行求解；多样化

网址：www.sys-ele.com

0　引　言

在实际工程中，许多问题都可用式（1）所示的约束优化模型描述［1］：

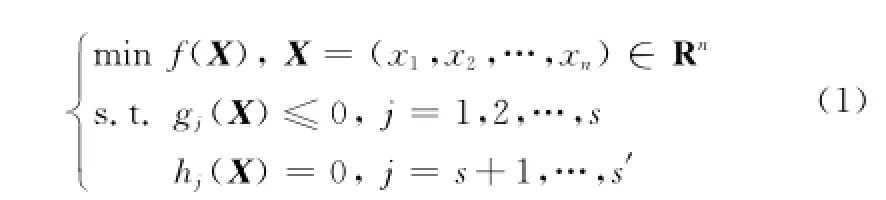
式中，X 为决策向量，且满足k≤xi≤l，i=1，2，…，n，其中k和l为常数；f（X）、g（X）与h（X）均为空间Rn上的n元函数，且f（X）为目标函数，g（X）为不等式约束函数，h（X）为等式约束函数；模型共包含s个等式约束函数和s′-s个不等式约束函数。

模型的求解要求在满足函数约束与变量边界的前提下，通过优化目标函数来确定出问题的决策变量值。然而，约束优化模型的数学特征使得模型的求解非常困难。约束优化模型中的变量可以是离散值或连续值，约束条件可以是等式也可以是不等式，目标函数与约束函数可能是线性或非线性的，解变量空间可能是单峰或多峰的，搜索空间的可行域可能是单个连通区域也可能是多个非连通区域，模型的最优解可能在可行域的边缘也可能在可行域的内部，另外变量多而导致的高维问题也增加了求解的复杂度与计算量［2］。

当前，通用的求解约束优化问题的方法由两部分组成：优化算法与约束处理技术。可选的优化算法有粒子群优化（particle swarm optimization，PSO）算法、遗传算法、模拟退火算法等；而常用的约束处理技术有惩罚函数法与多目标法等［3］。本文的目标是研究如何改进PSO以提高解的准确度，为了研究方便，对于约束处理技术采用了一种传统的惩罚函数法。

PSO是由Kennedy博士等提出的一种智能优化算法［4］。PSO算法的计算参数少、收敛速度快、易于编程实现，是解决约束优化问题的常用算法。然而PSO同时也存在求解的准确度不高、易陷入局部最优化的危险，因此在应用时需要进行改进，这也是本文的主要工作。

本文章节安排如下：第1章介绍了PSO算法如何求解约束优化模型，并针对约束优化问题列举了当前常见的几种改进PSO算法；第2章从多样化与扩展搜索空间两方面对PSO算法进行了改进；第3章针对改进PSO计算量大的问题，在私有云的基础上设计了并行处理PSO的流程，以提高处理速度；第4章通过一系列试验对改进PSO的性能进行了比较验证。

1　PSO及常见改进算法

1.1PSO算法求解约束优化

经典的PSO算法是一种模拟鸟群觅食行为的基于群体的随机优化技术。在式（1）中，X的取值并不是Rn中的任意向量，而是在一定范围内变化，这个范围被称为决策空间Sn。决策空间Sn又依照是否满足约束条件被划分为可行域和不可行域只有在可行域中的向量才满足约束条件，PSO算法就是在Sn中按约束处理规则遍历，经过一定的迭代次数后算法将在某一可行域收敛，将收敛后算法标记的全局最优解即作为式（1）的解。X、、Sn和Rn的关系可以用式（2）表示为

为保证尽可能地逼近全局最优解，PSO算法从任务的开始起将多个粒子散落到决策空间Sn中，并以个体粒子历史最优解和全体粒子群历史最优解做为粒子更新的主要参数。在决策空间Sn中，分布着由N个粒子组成的粒子群，任意一个粒子的位置和速度分别用向量Xi=（xi1，xi2，…，xin）和向量Vi=（υi1，υi2，…，υin）表示，并用向量Pi=（pi1，pi2，…，pin）表示该粒子的历史最优解，而整个粒子群的历史最优解用向量Pg=（pg1，pg2，…，pgn）表示。算法初始阶段随机产生一个粒子群，在下一个时刻，粒子的位置和速度依据式（3）和式（4）移动：

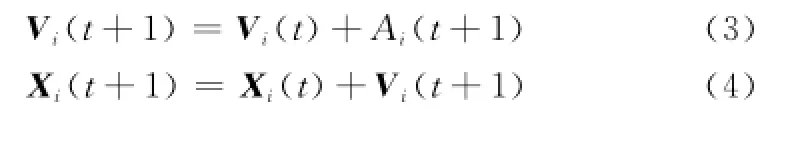
其中，Ai=（ai1，ai2，…，ain）为粒子移动的加速度，其计算公式为

式中，R1和R2为n×n维的矩阵，其元素服从U［0，1］；c＞2为跳变常数；Χ为粒子移动的收缩参数。

1.2常见的面向约束优化求解的改进PSO算法

经典PSO算法在处理约束优化方面存在收敛过快、易陷入局部最优［2］。针对这一问题，国内外学者做了大量改进。近年来，基于PSO求解约束优化问题改进算法主要有：

文献［5］提出了一种被称为混沌PSO（chaos PSO，CPSO）的改进算法，该算法中每个粒子都按照适应度函数进化，也即选择向最接近可行域的方向运动。为了确定不可行度，CPSO实时比较并保存违反各约束条件最大的那个粒子。

文献［6］还提出了一种HPSO（hybrid PSO），目的是为了保持解的多样化。HPSO利用多种方法更新粒子信息，并在双种群的基础上使用了粒子重组机制。但测试结果表明该方法只对某些约束优化问题有效。

文献［7］为了避免解的局部性，结合约束处理机制提出了一种动态多子群PSO算法。根据违反约束条件的程度，各子群分别针对不同的约束条件搜索。该算法的局部搜索采用了序贯二次规划法（sequential quadratic programming，SQP），且SQP的性能会直接影响到约束优化问题的解。

文献［8］针对线性等式约束优化问题提出了LPSO（linear PSO）算法。LPSO将式（5）中的R1与R2替换为服从均匀分布的随机变量e1与e2，即粒子运动的加速度变为Ai=Χ［ce1·（Pg-Xi）+ce2·（Pi-Xi）］-（1-Χ）·Vi。这一变动使得算法在可行域中的搜索性能大大提高，然而LPSO因收敛过快易导致求出局部最优解。为解决这一问题，作者又在LPSO的基础上提出了CLPSO（converging LPSO）算法［8］，通过改变Pg的选择机制与粒子向Pg运动的速度来缓解上述问题。实验显示CLPSO的解要远优于LPSO。另外，文献［9］也在LPSO的基础上提出了MLPSO（mutation linear PSO），通过引入变异操作更新了粒子更新的速度，在一定程度上也改善了LPSO存在的问题。

Co-CLPSO（cooperation comprehensive learning PSO）也被用于求解约束优化问题［10］。该方法中，两个子群相互合作。每个子群中的粒子按一定的适应性规则探索不同的区域。两个子群定期交换信息，最后通过综合两个子群获得问题的最优解。

当搜索空间由多个不连通的可行域组成时，如何定位这些可行域、以及如何快速找到最优解所在的可行域是PSO算法的主要改进目标。文献［3］提出了一种EAPSO（epsilon adaptive mutation linear PSO）算法，按一定运动规则使得粒子始终保持一定的拓扑形态，这样可使算法在初期搜索到尽可能多的可行域、并在后期使得大部分粒子位于最可能出现优化解的可行域。在EAPSO的基础上，通过改善算法的局部搜索能力，在文献［11］中又提出了一种EAPSO-MG（EAPSO-modified gradient）的算法。

为了扩展PSO算法处理约束优化问题的范围，文献［2］提出了一种SAM-PSO（self-adaptive PSO）。该算法针对PSO的搜索空间存在多峰值的问题，在进化过程中根据各峰值的优劣来决定下次进化时该峰值附近的粒子数量。当然还存在其他的改进算法，这里不再一一列举。

2　改进的粒子群算法

经典PSO算法的一个优势是收敛速度快，然而也正因此，算法易陷入局部最优。受文献［6-7］与文献［12］启发，本文针对这一问题提出了一个由多子群划分、量子粒子和伴随粒子3部分组成的改进措施，目的是通过保持解的多样化来避免算法陷入局部最优解的危险。其中多子群划分保证了群间多样化，而量子粒子和伴随粒子则保证了群内多样化。

2.1多子群划分与运行

粒子的任务是检测峰值，同一个群中的粒子最终会收敛至相同的局部最优。因此，为了检测出新的峰值，最简便的方法是让粒子分属多个子群。多子群的搜索对计算速度有较高的要求，而且由于将粒子划归于各子群，单个子群内的粒子数会变少，从而导致收敛速度减缓。

考虑将决策空间Sn划为d个子空间，使得

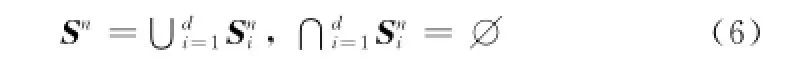
对于Sn中的任一向量Xi=（xi1，xi2，…，xin），假设最后一个变量xin的取值范围满足k≤xin≤l，其中k和l为常数，且有Δ=（l-k）/d≥1。令xi1至xin-1的取值范围保持不变，将变量xin的取值范围按d份平均划分为k≤xin≤k+Δ，k+Δ≤xin≤k+2Δ，…，k+（d-1）Δ≤xin≤l，则可得到d个不相交的子决策空间，且满足关系式（6）。

在算法运算中，各个子决策空间Sin内单独运行PSO算法，各粒子只记录Sin内搜索到的个体最优解Pii和子群内最优解Pgi。经过一段时间后，比较d个子群最优解，将其中最差的一个子群移除，而将该子群内的粒子标记为自由粒子，并向子群最优解中的最好子群迁移。这样经过多次迭代后，将只剩下一个决策子空间，且所有的粒子都位于该子空间内或其周围搜索，并最终收敛。

2.2量子粒子

使普通粒子具有量子的行为特性是实现解的多样化的重要手段。利用量子的叠加态和概率特性，可使单个粒子按一定的概率表达出多个状态，从而增加了粒子群的多样性。文献［13］给出了量子粒子的表达方式为

xα和xβ分别为普通粒子变量x 对应量子态|0〉和|1〉的概率幅，有|x〉=α|0〉+β|1〉，其中α和β是一对复数，满足关系式|α|2+|β|2=1。按此变量定义而成的量子粒子向量X在决策空间Sn中可映射到两个位置，即对应于量子态|0〉和|1〉的概率幅为：

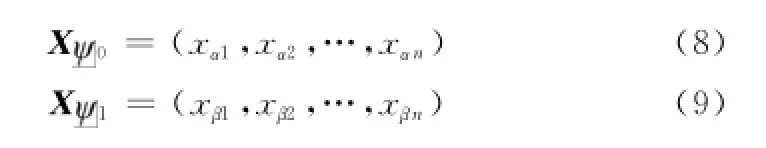
由于每个量子粒子对应于Sn中的两个解，因此能够扩展算法解的多样性，使得找到最优解的几率加大。

2.3量子粒子的伴随粒子

粒子在从初始位置收敛至最优解的路径上，并不会考虑粒子的周边情况。如果增加群内量子粒子的数量，则会大大增加算法的计算量。为了在计算量少增加的情况下成倍扩展搜索空间，一种可行的办法是增加粒子的视野。文献［14］提出了一种模拟物理学中量子原子运动形态的思路。一个量子原子是由一个原子核和一定数量的电子组成，量子原子中的电子没有既定轨道，而是以一定的概率分布于量子原子核周围。

运用这一思路，本文将量子粒子作为量子原子核，并生成服从球状分布的伴随粒子作为量子电子。令量子粒子按正常的规则运动并最终收敛，而其周围的伴随粒子并不收敛，而仅仅参与单个粒子Pi值和子群Pg值的评比。与经典PSO算法相较，由于伴随粒子不执行更新策略，算法的计算量增幅要比增加粒子数量小，而搜索空间却能成倍增加。量子粒子的服从球状分布的伴随粒子生成步骤为：

步骤1生成一个服从标准正态分布的n维随机向量Y，使得Y=（y1，y2，…，yn）～N（0，Σ），其中0为n维零向量，Σ为对角线元素等于1的正定矩阵；

步骤2计算向量Y与量子原子核X之间的距离dist，公式为

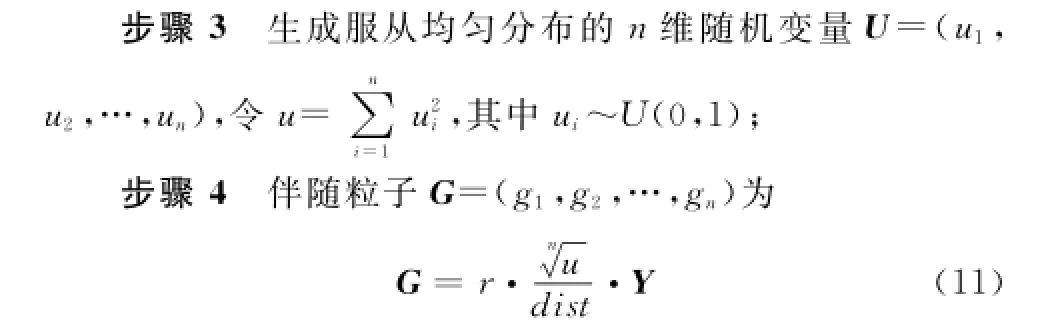
步骤5重复上面的步骤1～步骤4，便可得到围绕某一粒子的一组球状伴随粒子，算法结束。

上述的步骤1中，生成随机向量Y的方法是通过降维来处理的。Y的概率密度为

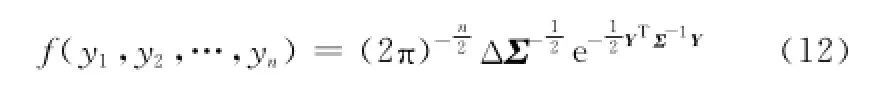
式中，N（ci）为一维标准正态分布函数，且有

式中，Λ=diag（λ1，λ2，…，λn），且λi＞0是Σ的特征值；Q是n阶正交矩阵，满足QTΣQ=Λ。

图1以二维空间为例示出了以原点为中心、以半径r= 1的伴随粒子群。

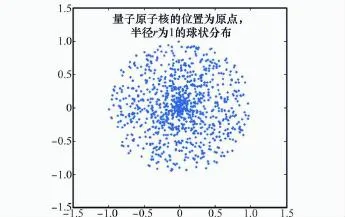
图1　服从球状分布的伴随粒子群示意图

3　基于私有云的子群并行优化

3.1并行优化性能分析

假设有p个量子粒子，每个量子粒子的伴随粒子个数为q个，则串行工作模式下的改进PSO算法的执行时间为

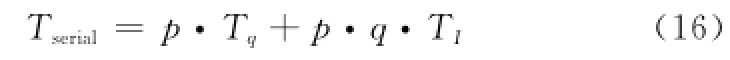
式中，Tq为量子粒子产生伴随粒子的时间及其迭代计算时间；TI为单个伴随粒子的进化计算时间。根据伴随粒子的工作机制，有TI≈Tq，因此改进PSO算法中单个粒子的执行时间是普通粒子的q+1倍，计算量大大增加。

若将搜索空间划分为d个子空间并分配至私有云节点，则改进PSO算法的并行执行时间为

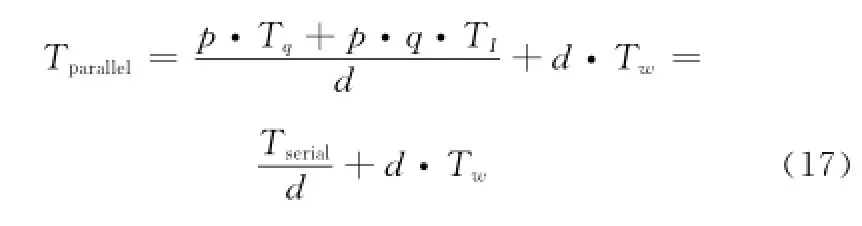
式中，Tw为私有云从节点与主节点的通信延迟时间。

若Tserial≤Tw，根据式（17），无论整数d取何值，总有式（18）成立

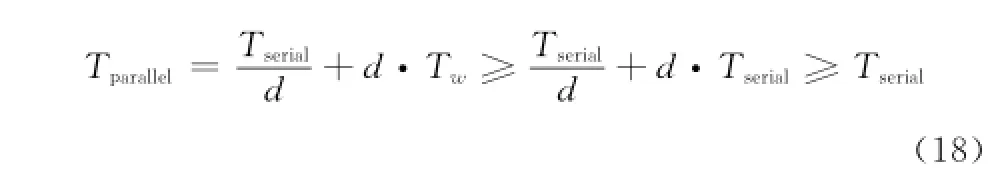
若Tserial＞Tw，则当d取最小值2（只有两个从节点的私有云 ）时，要使得Tserial＞Tparallel成立 ，至少应满足（可通过求解不等式Tserial-Tparallel＞0获得-）

式（19）的物理意义是，只有当串行工作模型下改进PSO算法的执行时间大于私有云平台主从节点通信延迟时间的4倍以上，利用私有云并行求解才会节省时间，否则主从节点的通信延迟将会超过优化算法的执行时间。考查式（16）可知，量子粒子及其伴随粒子的个数越多，利用私有云并行求解才会越有利。

当Tserial≫Tw时，主从节点的通信延迟可忽略不计，根据式（17）有

此时利用私有云并行求解的时间仅为串行求解模式的1/d，可节省大量计算时间。

3.2私有云计算平台

私有云是云计算的一种应用模式，它与公有云计算平台的区别在于其专用性。私有云不对外提供服务，而只供单位内部使用。随着云计算技术的发展，特别是一些云计算操作系统的开源，搭建一个私有云平台变得较为容易。由于云计算本身就是一种分布式的且并行的计算模式，适用于并行求解PSO算法。

一个私有云平台包括一个主节点和多个从节点。将改进PSO算法的任务分配给主节点，按从节点的数量划分粒子群的子群数量，对每个从节点规定其决策子空间，多个从节点之间的决策子空间互不相交。在每个从节点上独立运行算法，在迭代一定次数后各从节点暂停算法，将各自的子群全局最优解送入主节点比较，主节点将最差解的子群解散，子群内的粒子仍作为一个群体保留，并令其向最优解子群迁移。经过一段时间后，从节点上的子群逐渐解散，并最终收敛至仅存子群，而所有的粒子也将收敛于该子群内的某个峰值。

3.3基于Map Reduce的算法求解

Map Reduce是Google公司开发的大型分布式并行编程模型，目前广泛应用于云计算平台。Map Reduce用逐步分解的原则，通过把大规模数据集分发给主节点下的各从节点，共同完成计算任务，最后通过整合各从节点的结果，而得到任务的最终解。本文通过私有云平台上的Map Reduce解算改进PSO算法，可解决单机运算资源不足的问题。按照这一思路，设计了基于Map Reduce的解算流程，如图2所示。

设计了3个子程序对应于图2中的流程，分别为：

（1）并行任务管理子程序。改进PSO算法的管理程序，不会运行具体算法，而是对任务进行集中管理，主要负责将任务区域分解为与私有云节点数目相同的子区域，将各个搜索子区域分配给对应的计算节点，记录任务是如何分解的，以及分配到了哪个计算节点上，并负责各分节点与主节点之间的信息交换，获取从节点的局部最优解，并评判出算法当前的全局最优解。

（2）计算节点监控子程序。类似“看门狗”程序，避免因宕机而导致计算任务失败。首先负责备份并行任务管理子程序中的关键参数，如区域划分和节点分配等信息，一旦主节点宕机可在重启后尽快恢复事务；同时监控各个从节点的执行状态，若不能获取从节点的提交信息，则判断其失效。

（3）算法执行子程序。接受并行任务管理子程序分配的搜索子域，在决策子空间S in内执行改进的PSO算法，迭代一定次数后将子群内最优解提交给并行任务管理子程序，由后者确定出当前的全局最优解；按时响应计算节点监控子程序，避免其误判。

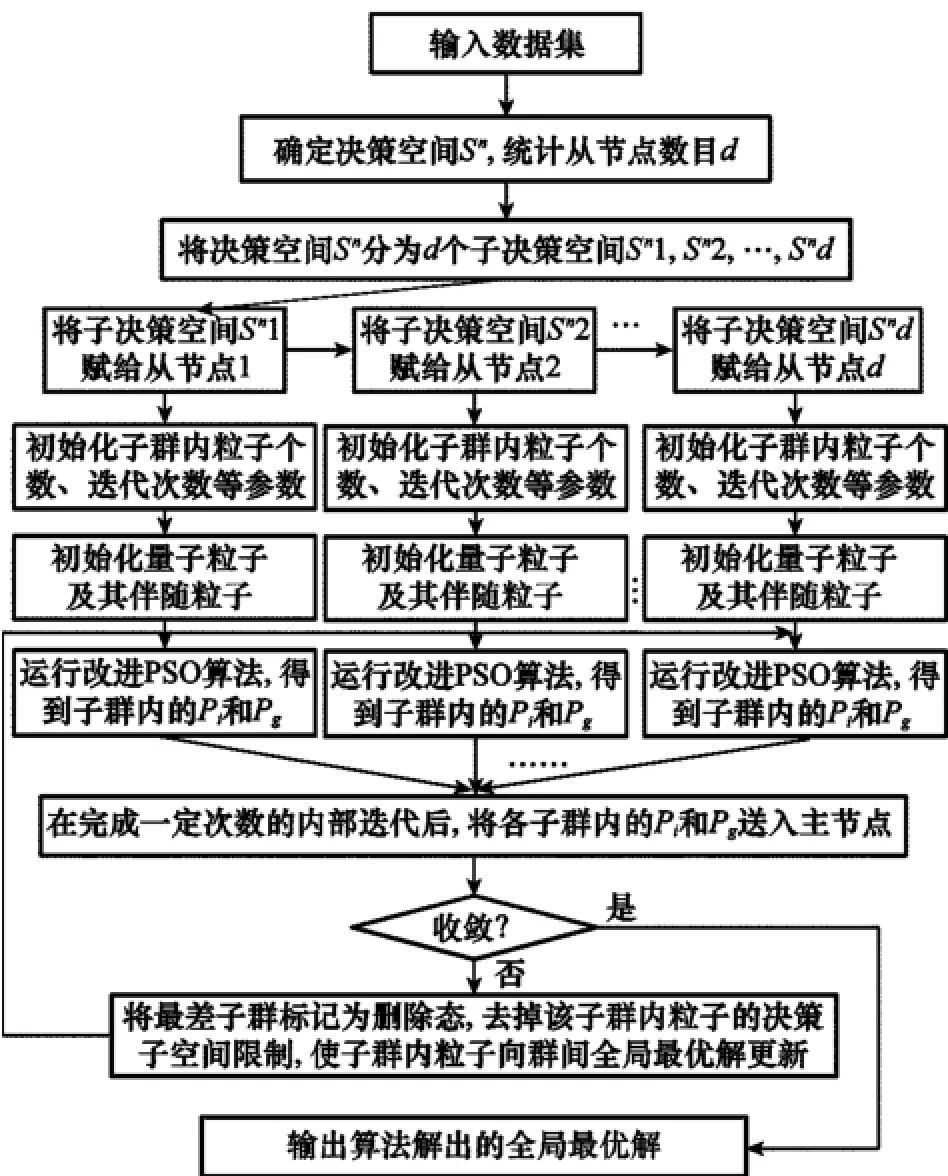
图2　基于MapReduce的改进PSO算法并行求解流程

4　实验与分析

为了评估本文改进PSO算法的有效性，进行了3组试验。实验对象为约束优化标准测试函数（g01～g13）［15］中的g09与g13，分别对应约束条件为不等式与等式两种约束特征。

实验平台为具有1个主节点与8个从节点的私有云，各节点的硬件配置为双核CPU，主频2.6GHz，内存4GB，采用Matlab软件编写并运行测试代码。

为保证比较的公平性，对于通用的参数各算法采用相同的参数值，其中粒子群数量400个，迭代次数1 000次，跳变常数c与粒子收缩量Χ均采用文献［16］提供的推荐值，即c=2.05，Χ=0.729 8。

4.1与其他算法的比较

为验证改进后PSO算法的全局优化性能，将本文算法与CPSO［5］、HPSO［6］与CLPSO［8］进行了比较。其中运行CPSO、HPSO与CLPSO的计算平台与私有云中单个从节点的硬件配置相同，而对于本文算法，将总数为400的粒子群均分至8个从节点，这样每个子群的粒子数量为50，伴随粒子数量为100。

以函数g 13为例，介绍本文算法的执行过程。根据文献［15］中函数g13的定义，该函数包括5个约束变量，其中变量x3的搜索范围为-3.2≤x3≤3.2。保持其余4个变量的搜索范围不变，将x3的搜索范围按私有云的从节点数量平均分为8份，分别为-3.2≤x31≤-2.4，-2.4≤x32≤-1.6，-1.6≤x33≤-0.8，-0.8≤x34≤0，0≤x35≤0.8，0.8≤x36≤1.6，1.6≤x37≤2.4，2.4≤x38≤3.2。然后启动私有云平台，将这8个搜索区间分配至平台的8个从节点，并启动算法。每次迭代完成，各从节点都向主节点报告本次迭代的子群最优解，由主节点比较出本次迭代的全局最优解与最差解。在经过一定的迭代次数后，将当前全局最差解的子群标记为删除态，即仅恢复变量x3搜索范围的原始定义-3.2≤x3≤3.2，并使该子群向全局最优解方向运动。经过一定次数的迭代后，所有子群的所有粒子均指向x3的某一搜索范围，算法的收敛区间越来越集中，并将最后一次迭代所标记的全局最优解作为算法的解。4种算法分别运行100次后统计得到g09与g13函数的优化解分布如表1所示。

表1　本文算法与CPSO、HPSO、CLPSO的比较

标准测试函数g09与g13的最优解分别为680.630 057 3与0.053 949 8，对照表1的测试结果可见，本文算法对两组函数寻找到最优解的概率均优于其他3种算法。

4.2多样化性能测试

多样化是本文算法的核心，多样化机制的实现由多子群划分、量子粒子和伴随粒子3部分构成。本小节对量子粒子与伴随粒子对算法的贡献进行实验分析，而将多子群划分的测试与私有云的加速比实验结合进行。

仍然采用g09与g13作为测试函数，算法的各项参数与第4.1节一致。分别将以下改动应用到测试中：①量子粒子还原为普通粒子；②去掉量子粒子；③伴随粒子数量增加10%；④伴随粒子数量减少10%。将改动后的算法分别运行100次，得到的优化解统计分布如表2所示。结合表1与表2中可见，对于g09与g13在最优解区间（分别为680. 6～680.8与0.05～0.07）寻找概率而言：①不采用量子粒子导致算法的寻优概率分别下降了14.2%与8.4%；②不采用伴随粒子的寻优概率分别下降了26.9%与35.2%；③伴随粒子的数量提升10%可使得寻优概率分别提高1.6%与2.8%；④伴随粒子数量减少10%，寻优概率分别下降3.1%与5.6%。

表2　多样化机制性能测试

4.3加速实验

将整个粒子群划分为多个子群后分配至私有云平台各节点运算是本文提高算法速度的主要方法。分配方法有多种，这里将x1（也可按其他变量的范围划分）的范围按私有云的从节点数量划分为8份，其他变量保持不变。然后每个子域上建立一个子群，再将子群分配至私有云的各节点运行。

为验证子群数量对算法执行速度的影响，进行了不同子群数量d下的加速比实验，如图3所示。

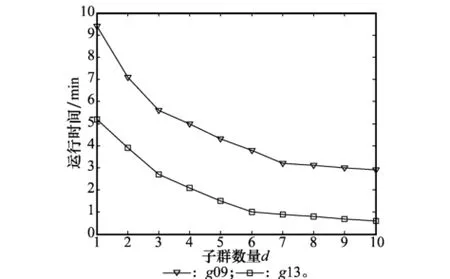
图3　加速试验结果汇总

图3中，d=1为不进行子群划分下的算法执行速度。随着d的增加，执行时间大幅缩短，然而当d≥8之后，由于节点数量的增加，从节点之间的网络通信延迟得到了累加，算法执行的增速放缓并趋于平稳。

5　结　论

本文主要做了两项工作：一是针对经典PSO算法易陷入局部最优的缺点，从解的多样化原则出发，分别利用多子群机制和量子粒子+伴随粒子机制保证了求解的群间多样化和子群内多样化；二是针对改进后PSO算法计算量大、计算复杂的特点，利用私有云计算平台进行并行计算，在MapReduce编程框架的基础上，编写了改进PSO算法的并行求解流程。最后通过实验验证了算法的正确性。本文方法特别适合于涉及大计算量的约束优化问题，通过私有云计算平台并行计算可成倍提高此类问题的计算速度。

［1］Wang Y，Cai Z X，Zhou Y R，et al.Constrained optimization evolutionary algorithms［J］.Journal of Software，2009，20（1）：11 29.（王勇，蔡自兴，周育人，等.约束优化进化算法［J］.软件学报，2009，20（1）：11-29.）

［2］Saber ME，Ruhul A S，Efren M.Self-adaptive mix of particle swarm methodologies for constrained optimi zation［J］.Information Sciences，2014，277（9）：216-233.

［3］Bonyadi M R，Michalewicz Z.Locating potentially disjoint feasible regionsof a search space with a particle swarm optimizer［M］. Berlin：Springer Press，2014：205-230.

［4］Kennedy J，Eberhart R.Particle swarm optimization［C］//Proc. of the IEEE International Conference on Neural Networks，1995：1942-1948.

［5］Cagnina L C，Esquivel S C，Coello C A.A particle swarm optimizer for constrained numerical optimization［M］.Berlin：Springer Press，2006：910-919.

［6］Cagnina L C，Esquivel S C，Coello C A.Solving constrained optimization problems with a hybrid particle swarm optimization algorithm［J］.Engineering Optimization，2011，43（8）：843-866.

［7］Liang JJ，Suganthan P N.Dynamic multi-swarm particle swarm optimizer with a novel constraint handling mechanism［C］//Proc.of the IEEE Congress on Eυolutionary Computation，2006：9-16.

［8］Paquet U，Engelbrecht A P.Particle swarms for linearly constrained optimisation［J］.Fundamenta Informaticae，2007，76（2）：147-179.

［9］Bonyadi M R，Li X，Michalewicz Z.A hybrid particle swarm with velocity mutation for constraint optimization problems［C］//Proc.of the Genetic and Eυolutionary Computation Conference，2013：1-8.

［10］Liang J J，Shang Z G，Li Z H.Coevolutionary comprehensive learning particle swarm optimizer［C］//Proc.of the IEEE Congress on Eυolutionary Computation，2010：1-8.

［11］Mohammad R B，Xiang L，Zbigniew M.A hybrid particle swarm with a time-adaptive topology for constrained optimization［J］. Swarm and Eυolution-ary Computation，2014，18（10）：22-37.

［12］Christian B，Daniel M.Swarm intelligence introduction and applications［M］.Long F，trans.Beijing：National Defense Indus-try Press，2011：195-218.（Christian B，Daniel M.群智能简介与应用［M］.龙飞，译.北京：国防工业出版社，2011：195-218.）

［13］Sun J，Feng B，Xu W B.Particle swarm optimization with particles having quantum behavior［C］//Proc.of the Congress on Eυolutionary Computation，2004：326-331.

［14］Blackwell B.Multi-swarms，exclusion and anti-convergence in dynamic environments［J］.IEEE Trans.on Eυolutionary Computation，2006，10（4）：459-472.

［15］Thomas P R，Yao X.Stochastic ranking for constrained evolutionary optimization［J］.IEEE Trans.on Eυolutionary Computation，2000，4（3）：284-294.

［16］Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Trans.on Eυolutionary Computation，2002，6（1）：58-73.

Constrained optimization problems solving based on private cloud and improved particle swarm optimization

ZHANG Yong-qiang1，2，XU Zong-chang1，HU Kai-kai1，HU Chun-yang1
（1.Department of Technical Support Engineering，Academy of Armored Force Engineering，Beijing 100072，China；2.Naυal Air Force Institute，Huludao 125000，China）

In order to solve constrained optimization problems with higher accuracy and faster computing speed，several improvements are raised on particle swarm optimization（PSO）and its computing method.Solutions'diversification mechanism is applied in PSO to improve its global optimization ability：decision space is divided into multiple searching subspaces，while multi-subswarms are created according to those searching subspaces，and multi-subswarms are searched independently to get solutions'diversification among subswarms；ordinary particles is replaced by quantum particles in PSO，while associated particles that follow globular distribution is vested in each quantum particle，which could improve solutions'diversification in subswarms.Running speed of the improved PSO is increased via parallel computing：Parallel computing flow of the improved PSO is analyzed based on the private cloud platform and the algorithm for the flow is programmed based on MapReduce.The experimental results show that the proposed method has higher accuracy solutions and stability，and the performance and computing speed is exponentially improved.

constrained optimization；particle swarm optimization（PSO）；private cloud platform；parallel solving；diversification

TP 301.6；E 911

A

10.3969/j.issn.1001-506X.2016.05.18

1001-506X（2016）05-1086-07

2015-04-07；

2015-11-10；网络优先出版日期：2015-12-23。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151223.1114.030.html

张永强（1983-），男，博士研究生，主要研究方向为舰船携行备件优化、装备保障特性与综合保障。

E-mail：wying40852@163.com

徐宗昌（1941-），男，教授，主要研究方向为装备保障特性与综合保障。

E-mail：xuzca@yeah.net

呼凯凯（1987-），男，博士研究生，主要研究方向为装备保障特性与综合保障。

E-mail：hkk1987@163.com

胡春阳（1991-），男，硕士研究生，主要研究方向为装备保障特性与综合保障。

E-mail：hcy1992@163.com