基于改进BP神经网络的机床基础部件可再制造性评价模型

潘尚峰　卢　超,2　彭一波

1.清华大学，北京，100084　　2.中国舰船研究设计中心，武汉，430064



基于改进BP神经网络的机床基础部件可再制造性评价模型

潘尚峰1卢超1,2彭一波1

1.清华大学，北京，1000842.中国舰船研究设计中心，武汉，430064

为了利用样本数据准确完成机床基础部件可再制造性评价，提高机床基础部件可再制造性评价预测精度，提出一种采用模拟退火遗传算法优化BP神经网络的机床基础部件可再制造性评价模型。该评价模型以机床基础部件可再制造性经典评价模型评价结果为样本数据，建立机床基础部件可再制造性评价BP神经网络预测模型，采用模拟退火遗传算法优化BP神经网络模型，寻找更优初始网络权值、阈值，以提高收敛速度和避免局部收敛。以一台机床基础部件可再制造性评价为例，验证了基于模拟退火遗传算法优化的BP神经网络评价模型具有更好的预测精度。

可再制造性；综合评价；BP神经网络；模拟退火遗传算法

0　引言

机电产品再制造是统筹考虑产品部件全寿命周期的系统工程[1]。再制造技术是绿色制造技术的重要分支，对重型机床实施再制造是最大限度地利用资源和减少环境影响的最佳“绿色制造”模式。重型机床再制造的核心是基础部件的再制造，评价基础部件的可再制造性是进行再制造的前提。国内外学者针对不同的评价对象提出了多种综合评价模型。张勇等[2]、劳兆利[3]结合层次分析法(analytic hierarchy process, AHP)与模糊综合评价法在确定评价影响因素权重的基础上，利用模糊评价方法减小权重的主观性，使评价结果更为准确。Rank等[4]提出数据包络分析方法，根据多项投入指标和多项产出指标，利用线性规划方法来评价多输入和多输出的相对有效性。Saaty[5]在AHP法基础上提出了网络分析法(ANP)，ANP法考虑评价指标之间的影响，通过求解超矩阵(Super Matrix)解决非独立层次结构问题。朱祖平等[6]、张中昱[7]利用模糊综合评价方法所得到的综合评价样本数据建立BP神经网络评价模型，使评价系统拥有自学习能力并且克服了评价的主观性和模糊性。冯冬青等[8]、郭晓婷等[9]采用遗传算法改进BP神经网络，针对不同评价对象进行综合评价，有效克服了BP算法易陷入局部收敛的缺点。

综合已有的文献可看出，针对评价对象的评价方法有很多种。传统的层次分析法未考虑评价指标间的相互影响，网络分析法虽然考虑了指标间的相互影响，但是超矩阵计算量过大。因此，本文利用指标间相关性法(CRITIC)求解部分权重，考虑了评价指标间的相互影响，且计算较为简便。数据包络法等诸多模型评价过程较为复杂，本文将模糊综合评价法和数学公式法相结合，计算基础部件可再制造性初始评价值。在建立传统基础部件可再制造性评价模型基础上，利用传统评价模型得到的评价数据构建基础部件可再制造性BP神经网络评价模型。相对于使用单一遗传算法对BP神经网络进行改进优化，采用模拟退火遗传算法(SGA)优化的神经网络具有更强的全局搜索能力和宏观优化性能，有效避免BP算法易陷入局部收敛的缺陷，提高了收敛速度。利用模拟退火遗传算法对BP神经网络的初始权值、阈值进行优化，再利用BP神经网络模型进行精确求解，从而使BP神经网络收敛到全局最小值，提高BP神经网络预测精度。

1　重型机床基础部件可再制造性BP神经网络评价模型

1.1重型机床基础部件可再制造性评价模型

重型机床基础部件可再制造性评价模型结构如图1所示。建立全面、准确的评价指标体系可以综合考虑多种因素对评价结果的影响，利用评价指标值量化数学模型得到基础部件各个二级评价指标值，结合初始评价指标值采用组合赋权法得到各个评价指标的权重，将初始指标评价值进行加权求和得到基础部件可再制造性综合评价值。

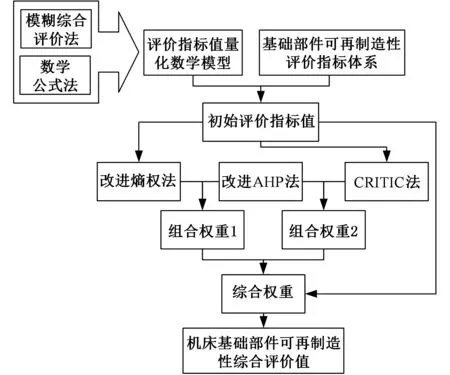
图1　重型机床基础部件可再制造性评价模型结构图

重型机床基础部件具有质量大、完整性好的特点，对基础部件实施具有资源节约特点的再制造具有更好的经济和社会效益。重型机床再制造主要针对床身、工作台、立柱、横梁、顶梁等质量较大的基础部件。基础部件可再制造性受多种因素的共同影响，综合机床再制造过程的影响因素，建立的重型机床基础部件可再制造性评价指标体系如图2所示。评价指标体系包含技术性、经济性等五个一级评价指标和若干个二级评价指标。评价指标权重采用主客观组合赋权法进行计算。改进熵权法和改进AHP法组合求解得到组合权重1，指标间相关性法和改进AHP法组合求解得到组合权重2，综合两个组合权重得到评价指标综合权重。

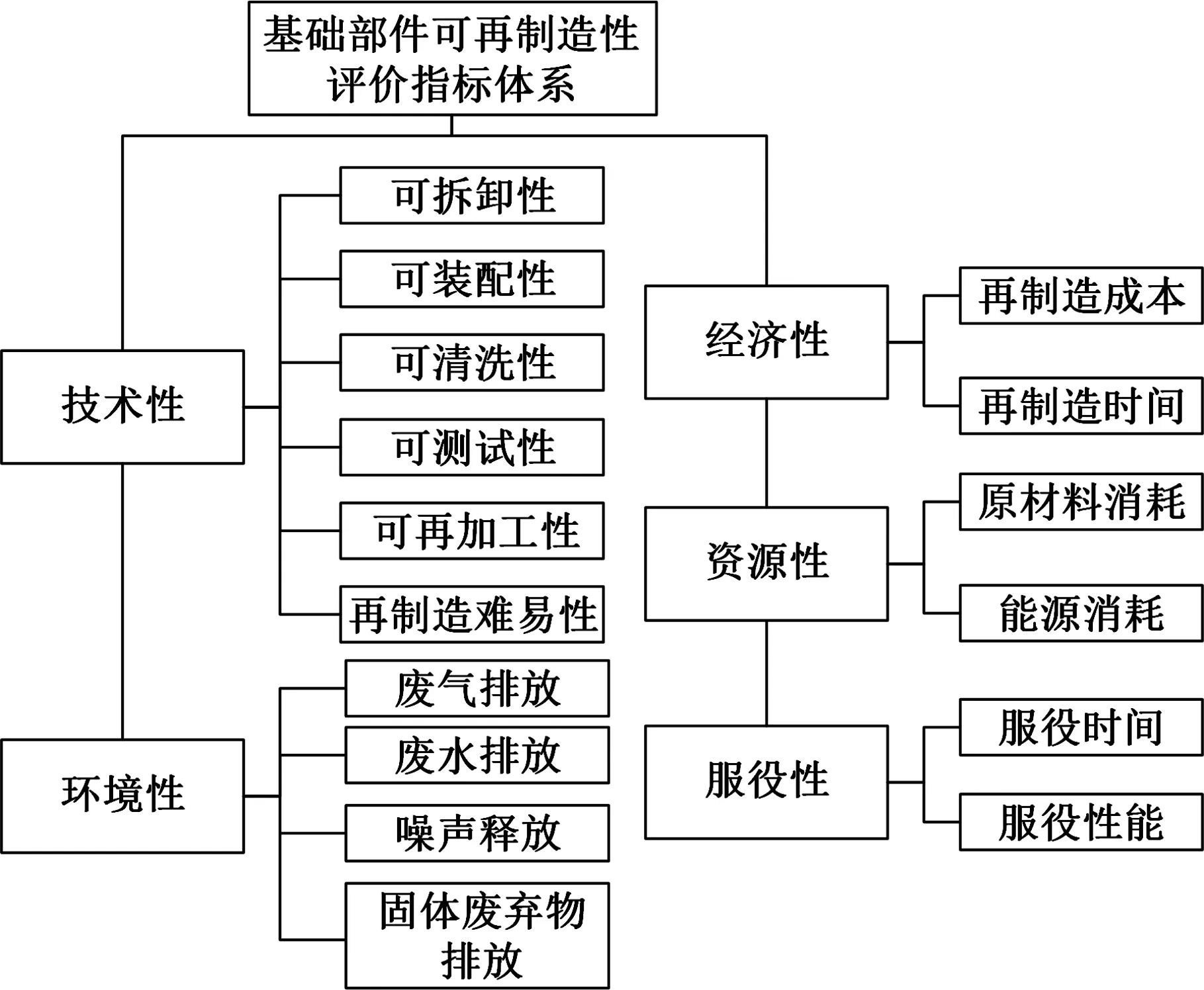
图2　基础部件可再制造性评价指标体系

评价指标值量化数学模型用于求解评价对象二级评价指标值。结合各二级评价指标的特点，本文提出模糊综合评价法和数学公式法计算二级评价指标值。模糊综合评价法通过建立评语集和评语集向量对评价指标值进行计算。选取评语集向量为WE=(1，0.8，0.6，0.4，0.2)T，评语集为{很好，好，较好，一般，差}。统计各个评价对象在各个评价指标上的评语集频数得到矩阵A，A中元素aij表示评价对象在评价指标i上评语集j的频数；计算隶属度矩阵B，B中元素，bij为评价对象在评价指标i上评语集j的比重，且有

bij=aij/m

(1)

式中，m为评定专家人数。

则采用模糊综合平均法求出的二级评价指标值为BWE。在评价指标中，技术性、环境性和服役性能评价指标值采用模糊综合评价法求出。

数学公式法针对的是能够通过数学公式直接求解的评价指标。经济性评价指标值、资源性评价指标值和服役时间评价指标值采用数学公式法直接求得。以再制造成本和服役时间评价指标值计算为例，再制造成本评价指标值计算公式为

(2)

式中，C1rem为基础部件再制造成本；C1new为新基础部件成本。

当再制造机床成本小于新机床成本时，该项评价指标值为节约的成本与新机床成本的比值，当机床成本小于新机床成本时，再制造失去经济价值，该项评价指标值为0。再制造服役时间评价指标值计算公式为

(3)

由m名专家评定，第i名专家评定某再制造基础部件剩余寿命为S1seri，评定再制造机床下一生命周期为S1lifei。

以一台正在进行再制造的INGERSOLL重型龙门铣床的基础部件可再制造性评价为例，通过上述评价指标值量化数学模型得到的基础部件可再制造性评价数据如表1所示，各评价数据均已归一化。

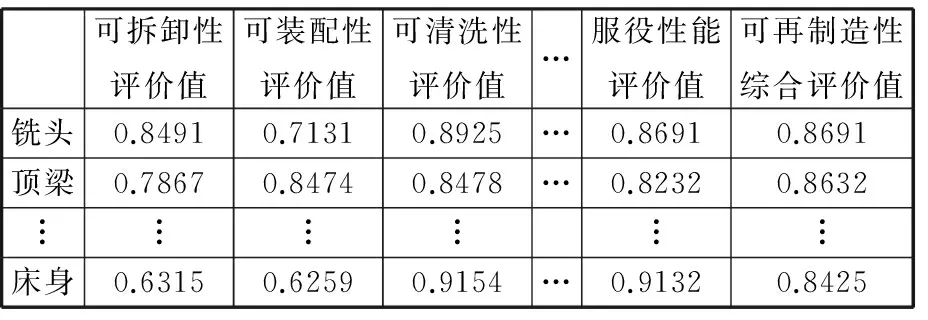
表1　基础部件可再制造性评价数据

1.2重型机床基础部件可再制造性评价BP神经网络构建

以传统的重型机床基础部件可再制造性评价模型得到的若干评价数据为样本，训练BP神经网络模型，建立重型机床基础部件可再制造性BP神经网络评价模型。由于三层BP神经网络模型就具有很好的非线性映射能力，因此隐含层选择一层，输入层为基础部件各个二级评价指标值，输出层为基础部件可再制造性综合评价值。基础部件可再制造性BP神经网络评价模型结构如图3所示。

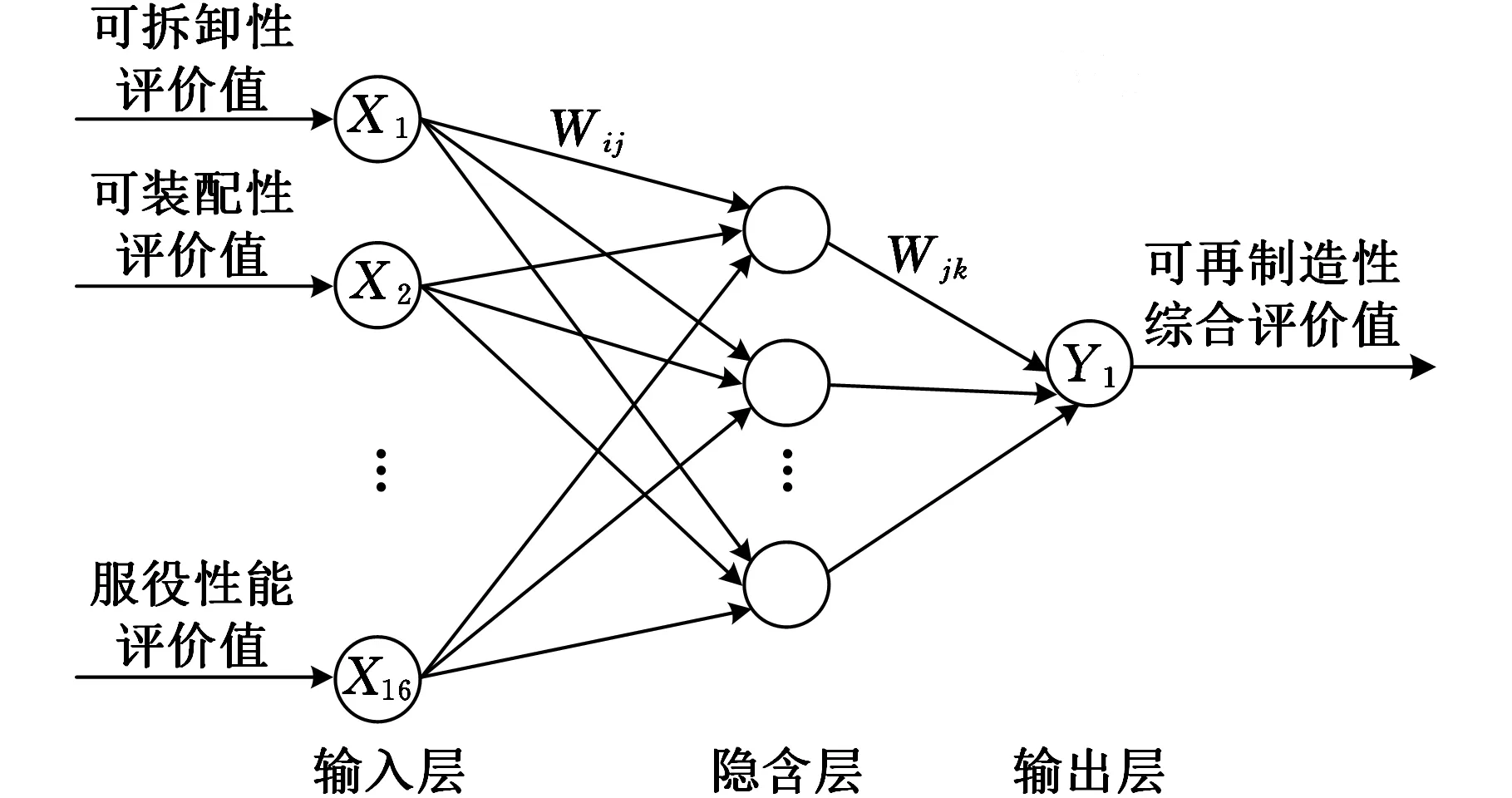
图3　基础部件可再制造性BP神经网络评价模型结构

为了提高收敛速度，BP神经网络训练函数选为trainlm函数。选取40组基础部件的可再制造性评价数据为训练样本，10组基础部件的评价数据为预测样本，分别测试不同隐含层节点数平均预测误差。不同隐含层节点数的对应BP神经网络的平均预测误差如图4所示。由图4可以看出，当隐含层节点数为20时，预测误差较低，因此BP神经网络模型隐含层节点数设为20。

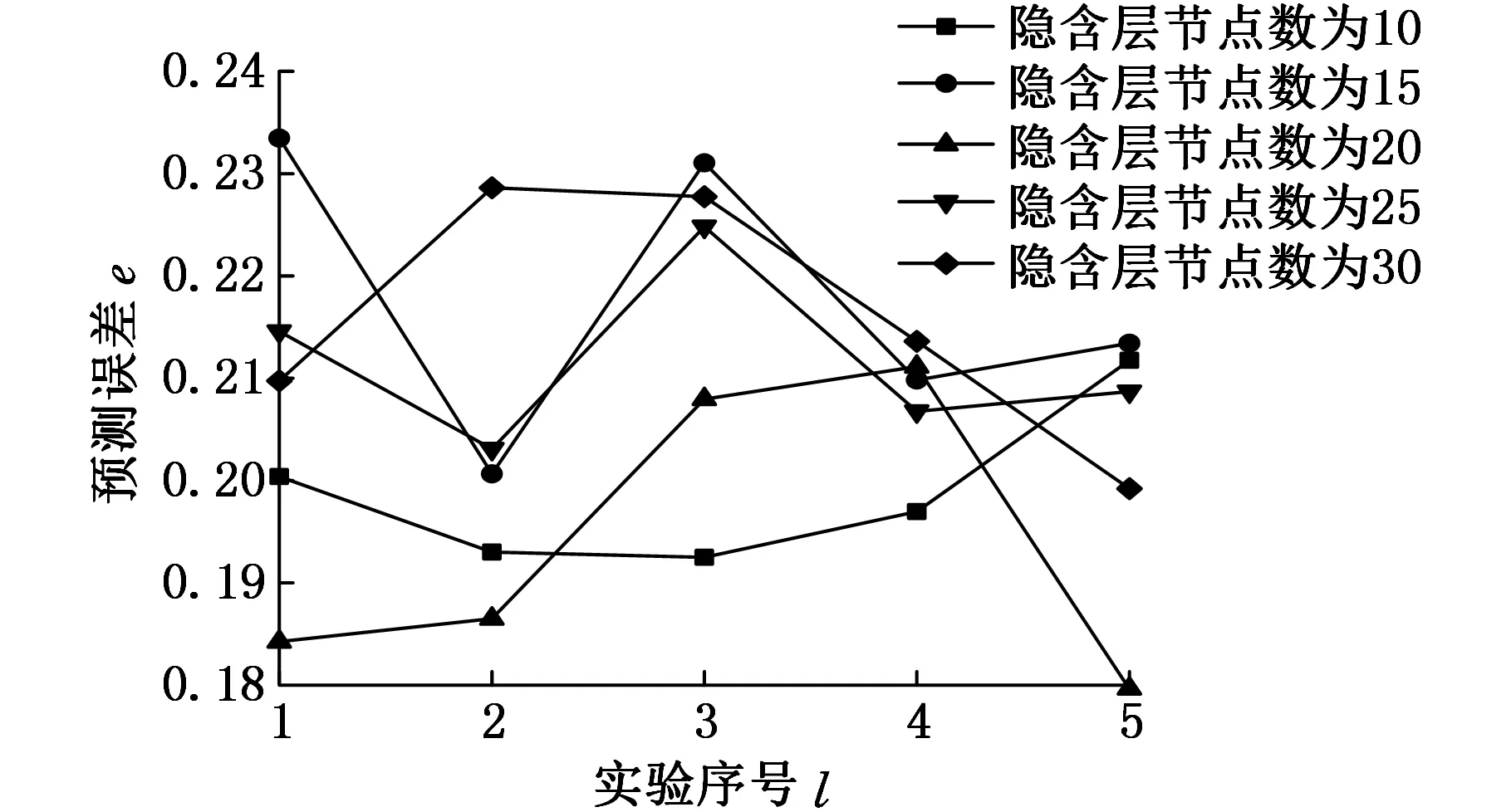
图4　不同隐含层节点数平均预测误差

2　模拟退火遗传算法优化BP神经网络

2.1模拟退火遗传算法原理

模拟退火算法是一种模拟固体退火过程的全局搜索算法[10]。模拟退火算法将优化对象目标函数用系统能量函数表示，通过模拟物体退火冷却至最低能量状态来达到全局搜索最优解的目的。选择一个初始状态xi代入退火算子并计算xi的能量函数值f(xi)，利用状态发生函数产生新状态xj并且计算新状态能量函数值f(xj)。若f(xj)≤f(xi)，则接受状态xj；若f(xj)>f(xi)，则以概率γ判断是否接受状态xj。γ的计算公式为

(4)

式中，T为当前迭代温度；k为比例因子。

设ξ为随机数发生器产生的范围为[0,1]的随机数，当γ>ξ时，状态xj为新的状态，否则状态仍为xi。

遗传算法是模拟生物在自然界中优胜劣汰的进化过程而形成的一种具有自适应性和全局搜索能力的概率搜索算法[11]。遗传算法能够自适应地控制搜索过程以求得最优解。在遗传算法中，个体或当前近似解被编码为染色体，染色体以二进制字符串表示，多个染色体个体构成进行寻优的种群。每一代个体将被计算出其适应度值，适应度较高的个体被选择进行变异和交叉的概率更高，交叉变异后产生新的种群，如此往复直到满足结束条件得到最优个体[12]。

适应度函数决定个体被选中的概率，个体适应度越高被选中的概率越大。一般采用预测输出与期望输出的绝对值之和作为个体适应度值，适应度函数为

(5)

式中，k′为比例因子；n为输出层网络节点数；yi和oi分别为网络实际输出和期望输出。

遗传算法有选择操作、交叉操作和变异操作三个基本操作[13]。

(1)选择操作。遗传算法通过选择适应性强的个体作为优良个体遗传给下一代。选择方法选用轮盘赌法，个体被选择的概率为

(6)

式中，N为种群规模。

(2)交叉操作。交叉操作通过选择操作选择两个基因Xk1和Xk2，分别在其染色体上第j位进行交叉操作，具体如下：

(7)

其中，r为[0，1]之间的随机数。

(3)变异操作。变异操作是以一定的概率改变种群中个体某些基因值，第i个个体的第j个基因Xij以概率Pv变异，变异规则如下：

(8)

式中，Xmax、Xmin分别为基因Xij的上下界；r1、r2为[0，1]之间的随机数；s为当前迭代次数；smax为最大进化次数。

2.2模拟退火遗传算法优化BP神经网络原理

采用模拟退火遗传算法优化的BP神经网络来预测基础部件可再制造性，其算法步骤如图5所示。

(1)初始化BP神经网络。根据输入输出要求确定输入输出节点数和网络层数，确定最大训练次数、训练精度等，确定隐含层节点数和初始网络权值、阈值。

(2)初始化模拟退火遗传算法参数。确定编码长度、种群大小、最大迭代次数和初始温度。

(3)模拟退火遗传算法迭代计算。进行染色体编码，计算个体适应度，选择适应度较大个体进行选择、交叉、变异和退火计算，优化种群个体，并且再次计算适应度，判断是否满足结束条件，迭代直至得到最优网络权值、阈值。

(4)利用最优网络权值、阈值训练BP神经网络，直到满足训练终止条件。

(5)利用训练好的BP神经网络进行基础部件可再制造性评价值预测，并且计算预测样本误差。

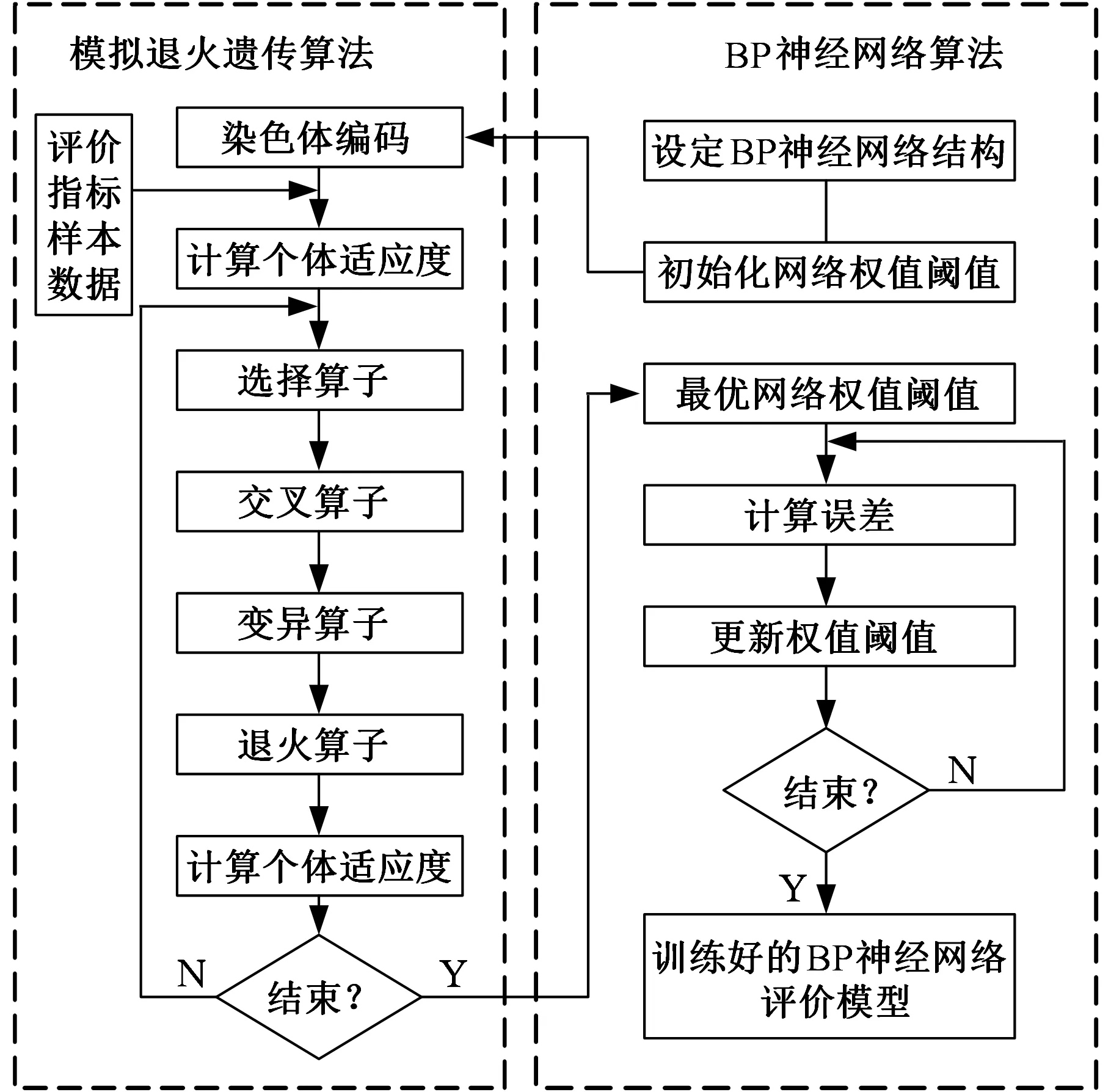
图5　模拟退火遗传算法优化的BP神经网络算法流程图

3　实验分析

在MATLABR2012a环境下，利用传统的重型机床再制造基础部件可再制造性评价模型得到若干基础部件可再制造性评价数据，以其作为样本建立BP神经网络，并研究模拟退火遗传算法优化的BP神经网络预测模型的预测精度。设置BP神经网络初始化参数如下：学习率为0.3，最大训练次数为2000，最大训练精度为10-20。设置遗传算法初始化参数如下：种群规模为50，遗传代数为100，交叉概率为0.1，变异概率为0.02，基因编码位数为20+2+16×20+20=362。二级指标评价值综合各个指标权重得到可再制造性综合评价值；以二级指标评价值为输入，神经网络预测输出可再制造性综合评价预测值，综合评价值和预测值的偏差即为预测误差。设置模拟退火算法初始化参数如下：初始温度为500。以40组样本数据为训练样本，10组数据为预测样本，对三种神经网络进行训练。以预测样本为输入，分别对三种网络进行5次训练和预测，得到每组预测样本在三种神经网络下对应的预测误差如图6所示。

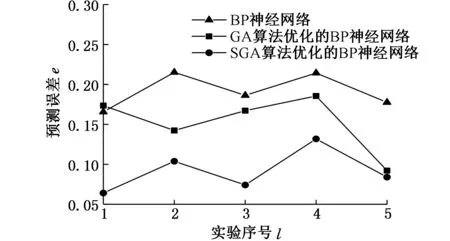
图6　10组预测样本对应不同网络的预测误差

由图6可以判断，相对于标准BP神经网络和单独由遗传算法优化的BP神经网络，经过模拟退火遗传算法优化的BP神经网络具有更好的预测精度。种群在迭代过程中，不同代数对应的均方误差变化如图7所示。由图7可以看出，当种群代数超过80时，种群迭代均方误差趋于稳定，随着种群迭代次数的增加，均方误差不会明显降低，因此采用最大迭代次数为100的合理性得到验证。

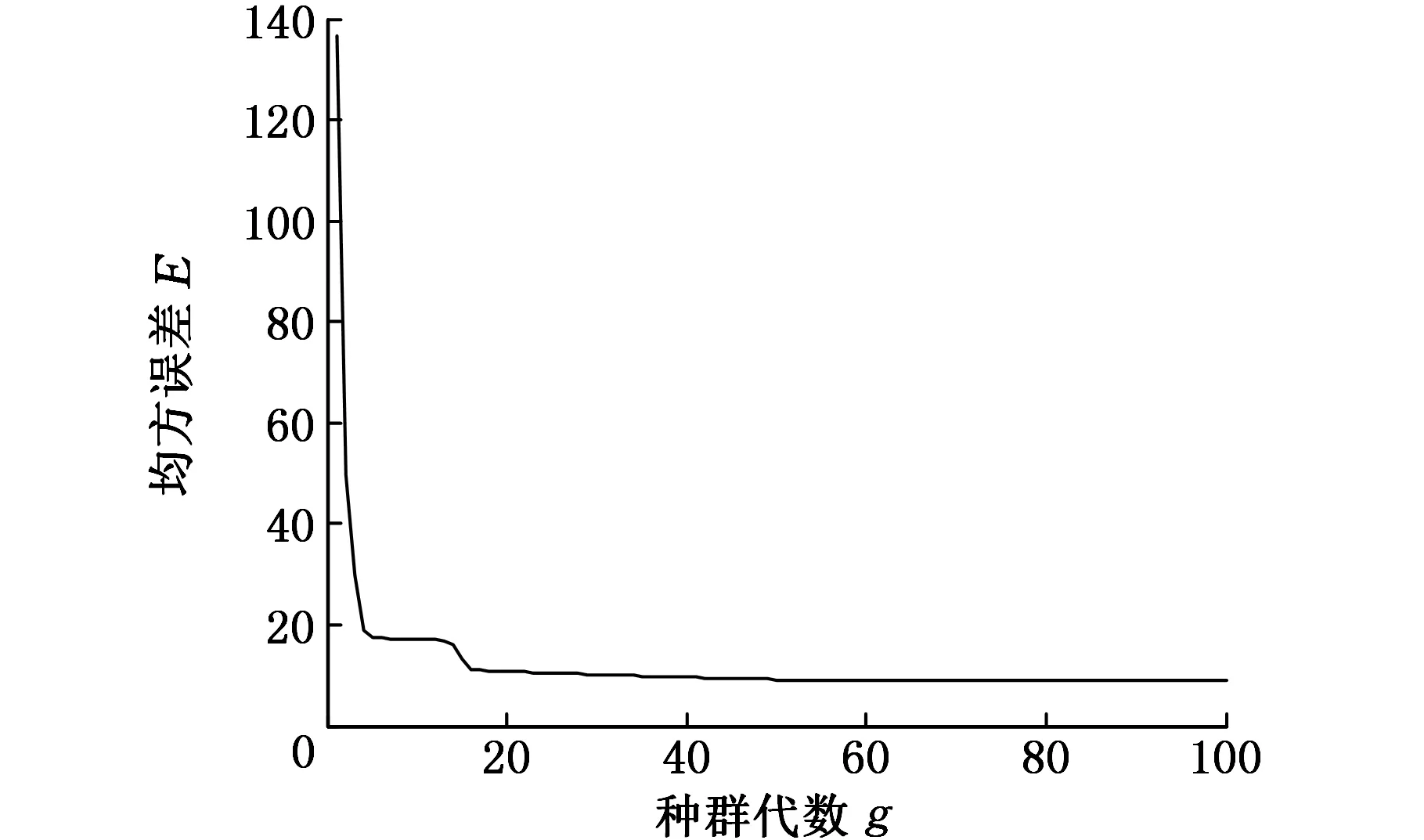
图7　不同种群代数均方误差

图8　重型卧式车床实物图

以一台重型卧式车床的基础部件可再制造性评价为例，该机床如图8所示。采用评价指标值量化数学模型求解出各基础部件二级评价指标值。以基础部件二级评价指标值为输入，利用SGA优化算法对BP神经网络进行训练，通过训练好的神经网络来对基础部件可再制造性进行预测分析。BP神经网络进行3次预测取平均值，预测结果如表2所示。根据评价指标值量化数学模型中的评语集和评语集向量，确定不同可再制造性综合评价值对应的可再制造等级如表3所示。一般认为可再制造性等级为Ⅰ级和Ⅱ级的基础部件适合进行再制造。由预测结果知，该机床床身、工作台、尾座和主轴箱可再制造性为Ⅰ级，具有很好的可再造性。刀架和中心架可再制造性为Ⅱ级，具有较好的可再制造性。

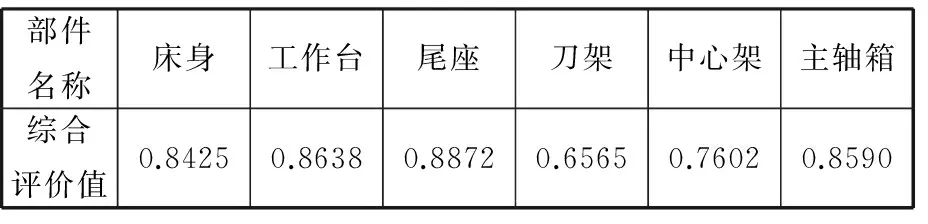
表2　基础部件可再制造性综合评价值

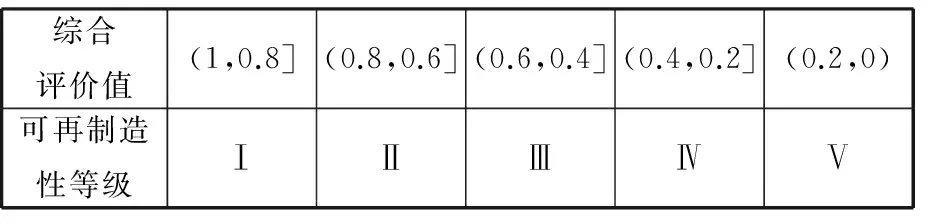
表3　可再制造性等级

4　结语

相对于传统机床基础部件可再制造性评价模型，BP神经网络评价模型具有高效、便捷等优点，因此建立基础部件可再制造性BP神经网络评价模型对传统评价模型的延伸与补充具有重要意义。由于采用了梯度下降法，所以BP神经网络存在容易陷入局部最优解的缺点，从而影响神经网络模型的预测精度。本文采用模拟退火遗传算法对BP神经网络初始权值、阈值进行优化，以提高神经网络的全局搜索能力，避免出现局部最优解。实验分析表明，模拟退火遗传算法优化的BP神经网络具有更高的预测精度。以一台重型卧式车床基础部件可再制造性评价为例，采用模拟退火遗传算法优化的BP神经网络评价模型预测出各基础部件可再制造性综合评价值，并确定出基础部件可再造性等级。

[1]徐滨士，张伟，马世宇，等. 面向21世纪的绿色再制造[J].中国表面工程，1999(4)：1-3.

Xu Binshi, Zhang Wei, Ma Shining et al. 21st Century Green Remanufacturing[J]. China Surface Engineering,1999(4)：1-3.

[2]张勇，林焰，纪卓尚. 基于AHP的运输船舶多目标模糊综合评判[J]. 系统工程理论与实践，2002(11)：129-133.

Zhang Yonghui, Lin Yan, Ji Zhuoshang. Multi-objects Fuzzy Comprehensive Evaluation of Sea-going Cargo Ship by AHP[J]. System Engineering Theory and Practice,2002(11)：129-133.

[3]劳兆利. 基于层次分析法与模糊综合评判法的集中运维点选择优化研究[D]. 上海：上海交通大学，2007:28-45.

[4]Rank R D ，Charnes A, Copper W W. Some Models Foe Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis[J]. Management Science,1984,30:1078-1092.

[5]Saaty T L. Decision Making with Dependence and Feedback[M]. Pittsburgh,PA:RWS Publication,1996.

[6]朱祖平，朱彬. 基于BP神经网络的企业技术创新效果的模糊综合评价[J]. 系统工程理论与实践，2003(9)：16-21.

Zhu Zuping, Zhu Bin. Fuzzy and Comprehensive Evaluation Based on BP Nerve Network to the Effectiveness of Technological Innovation in Enterprises[J]. System Engineering Theory and Practice, 2003(9)：16-21.

[7]张中昱. 基于BP神经网络和模糊综合评价的环境分析评价系统[D]. 天津：天津大学，2006.

[8]冯冬青，郭艳. 遗传算法改进BP神经网络在地下水水质评价中的应用[J]. 郑州大学学报(工学版)，2009，30(3)：126-129.

Feng Dongqing, Guo Yan. The Application of BP Nerve Network Optimized by Genetic Algorithm in Groundwater Quality Evaluation[J]. Journal of Zhengzhou University(Engineering Science), 2009, 30(3)：126-129.

[9]郭晓婷，朱岩. 基于遗传算法的进化神经网络[J]. 清华大学学报(自然科学版)，2000,40(10)：116-119.

Guo Xiaoting, Zhu Yan. Evolutionary Neural Network Based on Genetic Algorithm[J]. Journal of Tsinghua University(Natural Science), 2000, 40(10)：116-119.

[10]康立山，谢云.非数值并行算法——模拟退火算法[M].北京：科学出版社，1994.

[11]赵晶，唐焕文，朱训芝.模拟退火算法的一种改进及其应用研究[J].大连理工大学学报，2006，46(5)：776-780.

Zhao Jing, Tang Huanwen, Zhu Xunzhi.[J]. Journal of Dalian University of Technology, 2006, 46(5)：776-780.

[12]刘学士，肖旭，戴勇.基于遗传算法优化BP神经网络的磨削力预测[J].机械设计与制造，2013(1)：227-229.

Liu Xueshi, Xiao Xu, Dai Yong. BP Neural Network Based on Genetic Algorithm for Prediction of Grinding Force[J]. Machinery Design & Manufacture, 2013(1)：227-229.

[13]边霞，米良.遗传算法理论及其研究应用进展[J].计算机应用研究，2010，27(7)：2425-2428.

Bian Xia, Mi Liang. The Development of Genetic Algorithm Theory and Application[J]. Application Research of Computers, 2010，27(7)：2425-2428．

(编辑苏卫国)

Evaluation Model for Machine Tool Basic Parts Remanufacturability Based on Optimized BP Neural Network

Pan Shangfeng1Lu Chao1,2Peng Yibo1

1.Tsinghua University,Beijing，100084 2.China Ship Development and Design Center,Wuhan,430064

To utilize sample data to accomplish the remanufacturability evaluation of the machine tool basic parts, and to improve the prediction accuracy of remanufacturability evaluation of the machine tool basic parts, a BP neural network remanufacturability evaluation model optimized by the simulated annealing algorithm and genetic algorithm was proposed. A BP neural network remanufacturability evaluation prediction model of the machine tool basic parts was built according to the evaluation results of typical remanufacturability evaluation model. The BP neural network evaluation model optimized by the simulated annealing algorithm and genetic algorithm has better initial weights and thresholds to increase the convergence rate and avoid the local convergence. Remanufacturability evaluation of a machine tool basic parts was taken as an example to demonstrate that the remanufacturability evaluation model optimized by simulated annealing algorithm and genetic algorithm has higher prediction accuracy.

remanufacturability; comprehensive evaluation; BP neural network; simulated annealing genetic algorithm

2015-12-16

国家科技重大专项(2014ZX04014-011)

TP183

10.3969/j.issn.1004-132X.2016.20.009

潘尚峰，男，1961年生。清华大学机械工程系副教授。研究方向为机床可靠性绿色制造。卢超，男，1990年生。清华大学机械工程系硕士研究生，中国舰船研究设计中心助理工程师。彭一波，男，1989年生。清华大学机械工程系硕士研究生。