基于性能退化的小子样电主轴可靠性试验研究
邱荣华 巨孔亮 董友耕 屈萍鸽 刘宏昭
1.西安工程大学,陕西,西安,710048 2.西安理工大学,陕西,西安,710048
基于性能退化的小子样电主轴可靠性试验研究
邱荣华1巨孔亮1董友耕1屈萍鸽1刘宏昭2
1.西安工程大学,陕西,西安,7100482.西安理工大学,陕西,西安,710048
针对高速电主轴可靠性研究存在的问题,探讨了小子样电主轴性能退化可靠性试验方法,完成了两根170MD18Y16型电主轴的退化试验;依据选定的性能退化特征量和截尾时间,检测了主轴轴端径向跳动量,据此建立试样电主轴退化模型,分析其失效寿命;基于跳动量测试数据和Weibull分布函数,应用修正极大似然函数分析分布参数,得到170MD18Y16型电主轴特征寿命,并确定其寿命分布模型。电主轴寿命理论值与实际使用值基本一致,表明小子样电主轴性能退化试验方法合理,建立的退化模型较准确地反映了电主轴性能退化轨迹,且寿命分布模型分析方法有效。
小子样电主轴;性能退化;可靠性试验;轴端跳动量;退化模型
0 引言
为改进高速电主轴可靠性设计,提高国产电主轴可靠性水平,国内研究机构近年来相继开展了电主轴可靠性试验技术研究。电主轴作为高新技术产品,具有转速高、寿命长、造价高等特点,不仅难以完成加载及可靠性试验,受试验条件影响,还难以进行大样本、失效数据的可靠性理论分析。针对电主轴可靠性试验及理论分析存在的问题,邱荣华等[1]设计了高速电主轴电磁加载装置,解决了电主轴可靠性试验方法的问题。近二十年来,随着高可靠、长寿命产品可靠性分析的需要,研究者提出了小子样条件下基于性能退化量的无失效数据可靠性分析方法,为电主轴可靠性分析提供了理论基础。
目前,小子样条件下无失效数据处理与分析方法仍是可靠性理论研究的难点问题,主要原因在于,依据小子样性能退化试验检测的无失效数据难以准确分析产品退化轨迹模型和失效值,由此难以确定合理的寿命分布模型。针对此问题,多数研究均选用几种典型函数拟合退化模型,如线性、指数、幂函数及对数函数等,寿命分布模型则根据工程经验选择Weibull分布、正态分布或Beta分布函数等。根据上述小子样退化模型和寿命分布模型评估的产品寿命与实际使用值基本一致,上述方法不仅完善了可靠性理论,也很好地推动了可靠性理论在工程中的广泛应用。
基于性能退化量的小子样可靠性分析方法主要有虚拟增广样本法、贝叶斯法和极大似然法,Jayaram等[2]提出产品性能退化数据的分析模型,利用极大似然法对主轴产品实时可靠性水平进行了分析和预测;Xu等[3-4]提出了识别不明显退化量及动态系统实时可靠性水平的在线分析方法;Xu等[5]利用EM算法建立退化数据模型,据此分析了通用主轴可靠性指标;Wang等[6]利用模糊退化数据,提出基于竞争失效模式的可靠性分析方法;Zhao等[7]利用退化数据评估了金属化膜电容器的可靠性;Peng等[8]应用贝叶斯法评估了卫星的可靠性水平;朱德馨等[9-10]针对随机性能退化过程,应用混合Beta分布模型评估小样本高速列车轴承寿命;邓爱民等[11]利用加速退化试验数据建立武器装备性能退化量分布模型,并提出可靠性评估方法;傅惠民等[12]针对航空设备,提出Weibull分布定时无失效数据可靠性分析方法;金光[13]建立小子样航天轴承性能退化过程的Bayes层次化模型,应用虚拟增广样本法评估了轴承对数正态寿命分布参数;蒋喜等[14]分析了极小子样电主轴伪寿命分布及虚拟增广样本数,应用虚拟增广法评估了电主轴平均寿命等可靠性指标。
综上所述,基于性能退化量的小子样可靠性研究涉及诸多领域,但有关电主轴的可靠性研究资料并不多。为完善高速电主轴可靠性试验技术,本文探讨了小子样电主轴性能退化试验方法;针对170MD18Y16型电主轴性能退化试验,以轴端径向跳动量(位移)作为性能退化特征量,应用对数线性函数拟合两根试样电主轴退化量,建立退化轨迹模型,由设定的退化量失效阈值确定试样电主轴失效寿命;根据Weibull寿命分布,分析170MD18Y16型电主轴分布模型参数,确定其寿命分布模型。
1 性能退化试验装置
为完成电主轴可靠性试验,文献[1]设计了非接触电磁加载装置,通过直流电磁铁与加载盘相互作用,在主轴上产生电磁力,模拟主轴切削力载荷,以此实施可靠性负载试验。本文利用电磁加载装置设计了电主轴性能退化试验台,完成170MD18Y16型电主轴性能退化可靠性试验。具体方法如下:在加载装置产生电磁力载荷作用下,电主轴长时间、连续运行,其轴承出现磨损,使主轴轴端径向跳动量增大,该值达到设定值即可判定电主轴失效,故轴端径向跳动量为表征电主轴性能劣化的退化量;负载试验中,在定时截尾时间内实时检测该性能退化量,即可完成电主轴性能退化试验。图1所示为电主轴性能退化试验台,主要由电主轴、加载盘、直流电磁铁、直流电源、激光位移传感器和大功率轴流风机组成。其中,加载盘为高导磁铁镍合金圆盘,安装在电主轴轴端,直流电源采用恒流源为电磁铁提供励磁电流,经电磁铁产生直流电磁场,并经加载盘在主轴上形成电磁力载荷,实现电磁非接触加载;激光位移传感器用于检测电主轴轴端径向跳动量,采集性能退化量数据;大功率轴流风机用于电磁加载装置散热,使性能退化试验台可长时间连续运行。

图1 试验台实物图
2 截尾时间及性能退化特征量分析
高可靠、长寿命产品可靠性试验多采用小子样方法,针对复杂系统,考虑装置造价及试验条件,试验样本数可取1~2个[11,13],电主轴装置结构复杂、技术含量高、价格昂贵,故可靠性试验选取两根试样电主轴,样本数为2。根据电主轴性能,采用定时截尾方法判定试验终止时间,截尾时间依据GJB899A-2009标准进行判定,具体方法为:选取170MD18Y16型电主轴定时试验统计方案,确定两根试样电主轴总试验时间Td=2880h,则每根试样截尾时间Tr≥Td/2,即截尾时间Tr≥1440h。依据类似电主轴的平均寿命,本文设定Tr=1700h。在规定截尾时间内,连续若干个轴端径向跳动量测试值超过初始值的1.6倍,则终止性能退化试验;若到规定截尾时间,测试值未达到初始值的1.6倍,则按定时截尾试验原则,仍终止性能退化试验。
为准确获得电主轴性能退化数据及退化失效状况,需适当选取电主轴工作性能指标作为性能退化特征量。170MD18Y16型电主轴主要性能指标为前后轴承温升、主轴振动速度及轴端跳动量。电主轴在轴端径向载荷持续作用下,前后轴承磨损加剧,加大了轴承温升及主轴的振动,并导致轴端径向跳动量超过允许值,表现为主轴回转误差过大、丧失精度,造成电主轴失效。故轴端径向跳动量反映了主轴回转精度,确定其为电主轴性能退化特征量。
3 小子样电主轴退化轨迹模型
3.1退化量数据
文献[1]设定的电主轴可靠性试验条件为应力载荷Fy=81.1N,主轴转速9000r/min。按此试验条件,选用FT5070F型激光位移传感器检测170MD18Y16试样电主轴的轴端径向跳动量,按一定间隔时间连续采集轴端径向位移,一个采样周期内的实测波形如图2所示。

图2 轴端径向跳动量实测波形
一个采样周期时间显示的轴端径向跳动量幅值变化不大,随着采样时间的增加,轴端径向跳动量幅值将逐渐增大。根据采样间隔时间,整理的两根170MD18Y16型试样电主轴轴端跳动量部分实测数据如表1所示。
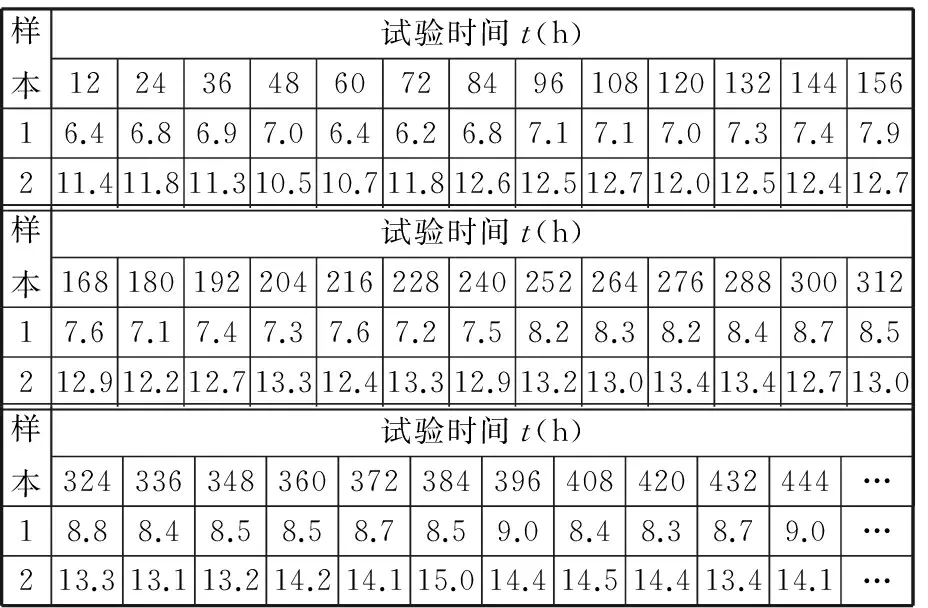
表1 电主轴性能退化试验数据(轴端径向跳动量) μm
3.2退化量建模
表1中测试数据按试验时间间隔12 h取值,试验时间应取至试验设定的截尾时间Tr=1700 h,轴端径向跳动量y为采样时间点的测试值。根据表1轴端径向跳动量数据,可建立退化量统计模型。该模型为电主轴的退化轨迹,表示退化量与时间变化关系。对于应力加载的性能退化试验,由磨损效应产生退化量,则退化轨迹方程可采用幂函数表示[11],即
y=atβ
(1)
对式(1)两边取对数,可得线性化方程:
lny=α+βlnt
(2)
式中,y为退化量;α、β为模型参数。
该模型实际表示退化量与时间的对数线性关系。设定失效阈值,根据退化量统计模型可得失效寿命。
表1中两根试样电主轴轴端径向跳动量数据分布点如图3所示,图中样本退化量分布点基本呈直线退化趋势。应用最小二乘法拟合样本退化量分布点,得到电主轴性能退化拟合曲线。
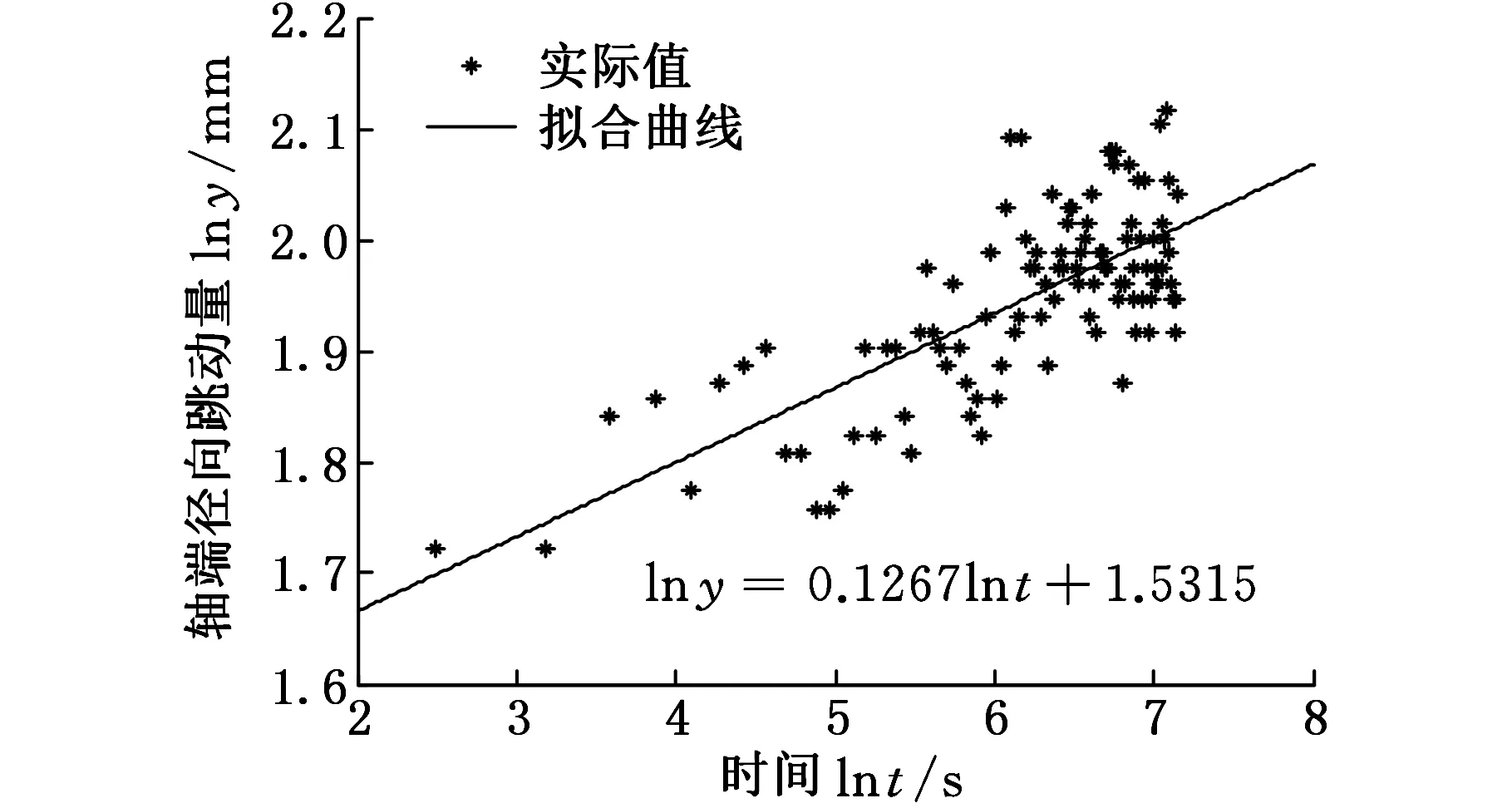
(a)样本1退化量拟合曲线
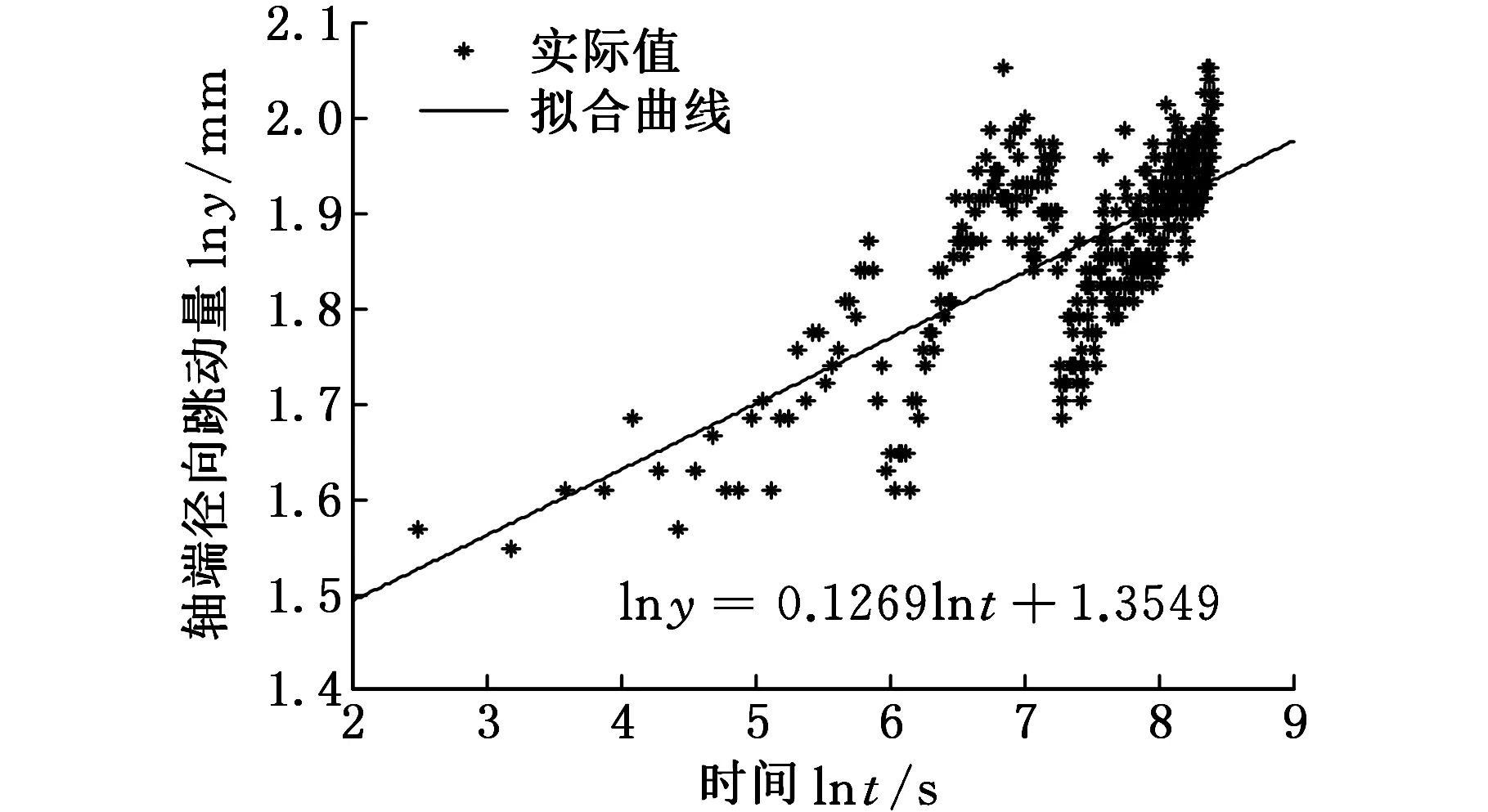
(b)样本2退化量拟合曲线图3 样本退化量拟合曲线
图3中拟合曲线表示电主轴轴端径向跳动量的实际退化轨迹。通过数据拟合,直接得到相应退化量拟合函数式如下:
样本1线性退化模型为
lny1=1.5315+0.1267lnt
(3)
样本2线性退化模型为
lny2=1.3549+0.1269lnt
(4)
式(3)和式(4)中所示直线退化模型与式(2)一致,表明退化模型与主轴磨损退化量经验分布模型相符。根据退化数据拟合的退化模型,可直接得到模型参数α和β的估计值,如表2所示。

表2 退化模型参数估计值与失效寿命
3.3退化模型假设检验
根据退化量试验数据,可选用经验分布函数对样本退化模型进行拟合检验[15]。经验分布函数Fn(t)是理论分布函数F(t)的较优估计,可表示为
(5)
计算检验统计量Dn,并确定Dn计算值中的最大值,方法如下:
(6)
式(6)中,Fn(t0)=0。
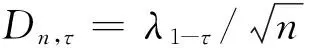
样本1幂函数退化模型
y1=4.625t0.0857
(7)
样本2幂函数退化模型
y2=3.876t0.0858
(8)
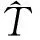
两根试样电主轴失效寿命存在一定偏差,主要原因如下:轴端径向跳动量为微米级,而FT5070F型激光位移传感器精度也为微米级,受试验条件限制,若选用更高等级精度的激光位移传感器,可明显提高跳动量测试精度,减小失效寿命误差;激光位移传感器安装支架需采用更有效固定方式,以减小周围环境对试验测试的影响;减小采样间隔时间,增大采样值数量也可有效减小误差。文献[14]给出170MD18Y16型电主轴实际使用寿命为2221 h,考虑误差影响及小子样条件,本文试样电主轴失效寿命均值与同类型电主轴实际寿命基本一致,表明小子样电主轴退化量建模方法有效。此外,本文失效阈值取值较为保守,适当降低失效阈值,可缩短试样电主轴失效寿命均值,更接近于实际使用寿命。
4 电主轴寿命分布模型及参数估计
根据小子样失效寿命,应用极大似然法或虚拟增广样本法可确定电主轴寿命分布模型。虚拟增广样本法需合理选择虚拟增广样本数,而样本数的确定有一定主观性,不同样本数分析的可靠性指标存在较大偏差。极大似然法可有效利用退化量测试数据计算寿命分布参数,并利用寿命分布验前、验后信息确定寿命分布置信限,分析结果较为准确。该方法先假定寿命分布函数,对于电主轴等高可靠长寿命机电产品,可假定寿命服从Weibull分布[15]。基于此,鉴于极大似然法已广泛用于小子样可靠性分析[2,11-12],本文针对两根试样电主轴的可靠性试验,应用改进极大似然法分析电主轴可靠性指标。该方法依据寿命分布函数推导出修正极大似然函数,并应用修正极大似然函数和性能退化试验数据估计分布参数,其估计值可取代真值,从而确定电主轴寿命分布模型,评定其可靠性指标[17]。
电主轴性能退化试验数据可表示为(ti,ni),i=1,2,…,k,针对Weibull分布函数,文献[17]推导了修正极大似然函数和分布参数估计式如下:
(9)
(10)
(11)
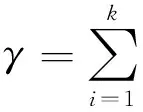
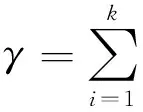
因修正极大似然参数估计值可取代真值,所以Welbull分布形状参数m=1.6472,尺度参数η=2494。Welbull寿命分布尺度参数η即为电主轴特征寿命,故170MD18Y16型电主轴寿命理论值为2494 h,而该型电主轴使用寿命为2221 h。对比可知,寿命理论值与实际使用值基本一致,表明本文分布模型及参数分析方法有效。
根据模型参数m和η计算值,可得170MD18Y16型电主轴Welbull寿命分布概率密度函数f(t)为
f(t)=4.1819×10-6t0.6472exp(-2.5388×10-6t1.6472)
分布函数F(t)为
F(t)=1-exp(-2.5388×10-6t1.6472)
5 结语
探讨了小子样电主轴性能退化试验方法,检测了两根170MD18Y16型电主轴性能退化数据;对试样电主轴轴端径向跳动量检测数据进行拟合,得到对数线性退化模型,完成模型假设检验,建立了170MD18Y16型电主轴幂函数退化模型;基于小子样轴端径向跳动量试验数据和Weibull分布函数,应用修正极大似然函数分析分布参数,确定170MD18Y16型电主轴寿命分布模型。
根据标准确定的失效阈值略为保守,致使样本失效寿命偏差较大,且均值与实际使用值存在一定偏差,后续研究应开展不同型号电主轴使用寿命统计分析,合理确定失效阈值,从而建立更为准确的退化模型,据此分析寿命分布模型及参数,提高理论分析准确性。本文研究补充了小子样电主轴可靠性试验及分析方法,对完善小子样电主轴可靠性试验技术具有重要意义。
[1]邱荣华,刘宏昭.高速电主轴非接触电磁加载装置设计与实现[J].中国机械工程,2014,25(8):1027-1032.
QiuRonghua,LiuHongzhao.DesignandImplementofHighSpeedMotorizedSpindle’sNon-contactElectromagneticLoadingSystem[J].ChinaMechanicalEngineering,2014,25(8):1027-1032.
[2]JayaramJSR,GirishT.ReliabilityPredictionthroughDegradationDataModelingUsingaQuasi-LikelihoodApproach[J].JournalofChemicalTechnology&Biotechnology, 2005, 85(3): 410-415.
[3]XuZhengguo,JiYindong,ZhouDonghua.Real-timeReliabilityPredictionforaDynamicSystemBasedontheHiddenDegradationProcessIdentification[J].IEEETransactionsonReliability, 2008, 57(2): 230-242.
[4]XuZhengguo,JiYindong,ZhouDonghua.ANewReal-timeReliabilityPredictionMethodforDynamicSystemsBasedonOn-lineFaultPrediction[J].IEEETransactionsonReliability, 2009, 58(3): 523-538.
[5]XuAncha,TangYincai.EMAlgorithmforDegradationDataAnalysis[J].JournalofEastChinaNormalUniversity, 2010,10(5): 38-48.
[6]WangZhonglai,HuangHongzhong,DuLi.ReliabilityAnalysisonCompetitiveFailureProcessesunderFuzzyDegradationData[J].AppliedSoftComputing, 2011, 11(3): 2964-2973.
[7]ZhaoJianyin,LiuFang.ReliabilityAssessmentoftheMetallizedFilmCapacitorsfromDegradationData[J].MicroelectronicsReliability, 2007, 47(2/3): 434-436.
[8]PengWeiwen,XiaoZhenlin,WangYanyan,etal.ACombinedBayesianFrameworkforSatelliteReliabilityEstimation[C]//InternationalConferenceonQuality,Reliability,Risk,Maintenance,andSafetyEngineering.Xi’an:IEEE, 2011: 13-21.
[9]朱德馨,刘宏昭.随机性能退化下极小样本高速列车轴承的可靠性评估[J].机械科学与技术,2013,32(10):1499-1504.
ZhuDexin,LiuHongzhao.ReliabilityEvaluationofHigh-speedTrainBearingBasedonStochasticPerformanceDeteriorationwithMinimumSample[J].MechanicalScienceandTechnology,2013,32(10):1499-1504.
[10]朱德馨,刘宏昭.混合Beta分布下高速列车轴承的可靠性寿命评估[J].机械科学与技术,2014,33(5):763-768.
ZhuDexin,LiuHongzhao.ReliabilityLifeAssessmentofHigh-speedTrainBearinginMixedBetaDistribution[J].MechanicalScienceandTechnology,2014,33(5):763-768.
[11]邓爱民,陈循,张春华,等.基于性能退化数据的可靠性评估[J].宇航学报,2006,27(3):546-552.
DengAimin,ChenXun,ZhangChunhua,etal.ReliabilityAssessmentBasedonPerformanceDegradationData[J].JournalofAstronautics,2006,27(3):546-552.
[12]傅惠民,张勇波.Weibull分布定时无失效数据可靠性分析方法[J].航空动力学报,2010,25(12):2807-2810.
FuHuimin,ZhangYongbo.MethodofReliabilityAnalysisforTimeTruncatedZero-failureDataBasedonWeibullDistribution[J].JournalofAerospacePower,2010,25(12):2807-2810.
[13]金光.小子样条件下航天轴承性能可靠性建模与评估[J].国防科技大学学报,2010,32(1) :133-137.
Jing Guang.Performance Reliability Modeling and Estimation for Space Bearing under Small Sample Circumstance[J].Journal of National University of Defense Technology,2010,32(1):133-137.
[14]蒋喜,刘宏昭,刘丽兰,等.基于伪寿命分布的电主轴极小子样可靠性研究[J].振动与冲击,2013,32(19):80-85.
Jiang Xi,Liu Hongzhao,Liu Lilan,et al.Extremely Small-scale Sample’s Reliability of an Electric Spindle Based on Distribution of False Lifetime [J]. Vibration and Shock,2013,32(19):80-85.
[15]兑红娜,孙秦.小子样疲劳试验数据的特征寿命估算方法评估[J].航空工程进展,2013,4(4):515-521.
Dui Hongna,Sun Qin.Evaluation of Characteristic Life’s Estimation Methods for Small Sample Fatigue Test Data[J]. Advances in Aeronautical Science and Engineering,2013,4(4):515-521.
[16]赵宇.可靠性数据分析[M].北京:国防工业出版社,2011.
[17]刘晗.基于Bayes理论的小子样可靠性评定方法研究[D].长沙:国防科学技术大学,2006.
(编辑苏卫国)
Research on Reliability Test Based on Small Sample Motorized Spindle Performance Degradation
Qiu Ronghua1Ju Kongliang1Dong Yougeng1Qu Pingge1Liu Hongzhao2
1.Xi’an Polytechnic University,Xi’an,710048 2.Xi’an University of Technology,Xi’an,710048
To avoid the disadvantages of reliability analysis on high-speed motorized spindle, a performance degradation reliability test method was proposed herein by two 170MD18Y16 motorized spindles. Firstly, according to the feature quantity and truncated time, a model of small sample motorized spindle was established with shaft end radial run out data to analyze failure life. Secondly, the characteristic life model of 170MD18Y16 motorized spindle was based on the data and Weibull distribution to analyze the distribution parameters by modified maximum likelihood function. Finally, the characteristic life of motorized spindle is consistent with the actual value. The results indicate that the method of performance degradation reliability test is reasonable, and the degradation model may reflect the performance degradation trajectory.
small sample motorized spindle; performance degradation; reliability test; run out data of shaft end; degradation model
2015-12-23
陕西省教育厅科研计划资助项目(15JK1309);西安工程大学博士科研启动基金资助项目(BS1503)
TH113.1
10.3969/j.issn.1004-132X.2016.20.008
邱荣华,男,1974年生。西安工程大学机电工程学院副教授、博士。主要研究方向为高速电主轴可靠性试验技术、机电系统测试技术。巨孔亮,男,1988年生。西安工程大学机电工程学院助理工程师、硕士。董友耕,男,1963年生。西安工程大学机电工程学院副教授。屈萍鸽,女,1977年生。西安理工大学机械与精密仪器工程学院讲师。刘宏昭,男,1954年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。

