工业机器人倍四元数轨迹规划算法的研究

李宏胜　汪允鹤　黄家才　施昕昕

南京工程学院，南京，211167



工业机器人倍四元数轨迹规划算法的研究

李宏胜汪允鹤黄家才施昕昕

南京工程学院，南京，211167

针对工业机器人在笛卡尔空间的轨迹规划曲线的平滑性与实时性，提出一种用于描述超球面旋转的倍四元数对机器人运动轨迹进行球面线性插补，并结合正弦波加速度曲线升降速控制算法对轨迹规划的速度进行控制，为机器人的轨迹规划提供了一种新的位姿规划的解决方案。在六关节搬运机器人控制系统平台上进行了仿真与试验，验证了该算法解决方案的有效性。

工业机器人；倍四元数；正弦波加速度曲线；轨迹规划

0　引言

工业机器人在笛卡尔任务空间内的轨迹规划包括位置插补、姿态插补以及速度、加速度、加加速度曲线的规划[1]。对于工业机器人的轨迹规划，通常采用笛卡尔空间的欧拉角法、等效轴法对姿态参数进行插补，但欧拉角存在万向死锁的缺陷，而等效轴法在旋转量为0时存在无法确定旋转轴的问题[1]。使用四元数法[2-4]可解决机器人在姿态插补中遇到的上述问题，但轨迹的位置插补则需使用其他的插补算法[5]，运算复杂，影响控制系统对轨迹规划的实时性要求。

本文对工业机器人在笛卡尔空间的轨迹规划进行研究，在进行正弦波加速度曲线[6]运动速度控制的同时，采用倍四元数[7-8]将笛卡尔空间中的机器人位置与姿态转换至四维空间，用超球面旋转对机器人的运动轨迹进行球面线性插补，转换过程误差可控[9]，且其中的乘法运算比齐次矩阵坐标变换矩阵方法的乘法运算要少。因此，该方法不仅能够满足C2连续，并且运算量较小，具有较好的实时性。

1　姿态四元数描述

四元数在动画制作、飞行器姿态控制以及工业机器人轨迹规划等领域具有重要作用[3-4]，是实数、复数以及三维空间矢量的扩充，它由四个元素组成，包含一个实部和三个虚部，表达式为

Q=s+xi+yj+zk=s+u

(1)

其中，x、y、z为实数；s为四元数的实部；u为虚部，表示单位矢量旋转轴(x,y,z)；i、j、k为虚数单位，并满足i2=j2=k2=ijk=-1。

在三维空间坐标系OXYZ中，刚体绕单位矢量轴u旋转σ角度，如图1所示，可用单位四元数表示为

(2)

图1　单位四元数旋转示意图

坐标系中任一点位置P1绕单位矢量轴u旋转σ角度到达P2，用欧拉角表示为

P2=RP1

(3)

式中,R为3×3的单位旋转矩阵。

用四元数表示刚体旋转[10-11]，则有

P2=QP1Q*

(4)

式中,Q为对应旋转矩阵R的单位四元数;Q*为四元数Q的共轭。

刚体旋转的欧拉定理表明，任意旋转都可以简化为刚体绕着固定轴的一次旋转。已知机器人的姿态旋转矩阵R，其对应的旋转四元数Q的实部s和虚部u如下：

(5)

式中,rij为姿态旋转矩阵R中第i行第j列元素。

已知旋转四元数Q，其对应的姿态旋转矩阵R如下：

R=

(6)

2　机器人运动学方程的倍四元数表示

2.1倍四元数描述

倍四元数把三维空间中的位置和姿态变换统一表示为四维空间中的双旋转[7-8]，其表达形式为

(7)

其中，ξ和η为倍四元数符号，且满足ξ2=ξ，η2=η，ξ+η=1，ξη=0；G部和H部均为单位四元数。

(8)

即倍四元数的G部和H部可单独计算，从而可简化姿态变换和倍四元数插值计算。

2.2数值计算法

给定三维空间中位姿矩阵的计算精度δ和机器人工作空间的最大边界L时，可通过公式

Rl=L/δ1/2

(9)

得到四维空间超大球的半径Rl。在笛卡尔空间中将机器人的位置和姿态变换矩阵转换为倍四元数的算法如下：

(1)对如下机器人末端位姿矩阵T：

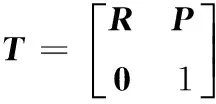
采用式(5)将姿态旋转矩阵R转换成旋转四元数Q，且平移向量P=(px,py,pz)T。

(2)将三维空间的平移向量P近似转换成四维空间的四元数，转换公式如下：

D=cos(ψp/2)+sin(ψp/2)up

(10)

其中，ψp=|P|/Rl，up为平移向量上的单位矢量，up=P/|P|，当|P|=0时，up为零矢量。

(11)

其中，Q由式(5)所得，即机器人末端姿态对应的四元数。

(4)对倍四元数的双旋转轨迹进行离散化得到一系列插值倍四元数点，需要将其转换成旋转四元数和平移向量，则转换算法如下：

Q=(G+H)/(2cosψ)

(12)

(13)

2.3连杆矩阵法

根据机器人连杆坐标系的D-H参数，将机器人相邻两个坐标系Oi-1Xi-1Yi-1Zi-1和OiXiYiZi之间的位姿关系用倍四元数进行描述。

坐标系Oi-1Xi-1Yi-1Zi-1绕Zi-1轴旋转关节角度θi，沿Zi-1轴平移di(di为机器人相邻连杆偏距)，即平移di=0i+0j+dik，用四元数表示为

Q=cos(θi/2)+0i+0j+sin(θi/2)k

(14)

结合给定的姿态矩阵R，由式(5)、式(10)、式(11)可转换为倍四元数:

(15)

即

(16)

γi=|di|/Rl

同样，坐标系Oi-1Xi-1Yi-1Zi-1绕Xi轴旋转连杆转角αi、平移ai=ai+0j+0k(ai为机器人关节连杆长度)，则可用倍四元数表示为

(17)

即

(18)

ρi=|ai|/Rl

由式(16)、式(18)，机器人各个关节齐次变换矩阵均使用倍四元数表示，运用式(8)倍四元数乘法，可得机器人末端执行器相对于基坐标系的位姿，用倍四元数表示为

即

(19)

式中，n为机器人关节数量。

由于倍四元数的G部和H部可独立运算，故式(19)可用如下两个表达式表示：

(20)

(21)

3　正弦波加速度曲线运动规划

为满足工业机器人轨迹的平滑性要求，采用正弦波加速度曲线速度控制算法对机器人轨迹进行升降速控制，如图2所示，其加加速度呈现余弦曲线，可以保证机器人运动轨迹的平滑性，减小机器人关节机构的机械振动[6，12-13]。图2中，ps、pe分别为起止位移，vs、ve分别为起止速度，va、vb为两个过渡点速度，amax为最大加速度，jmax为最大加加速度。

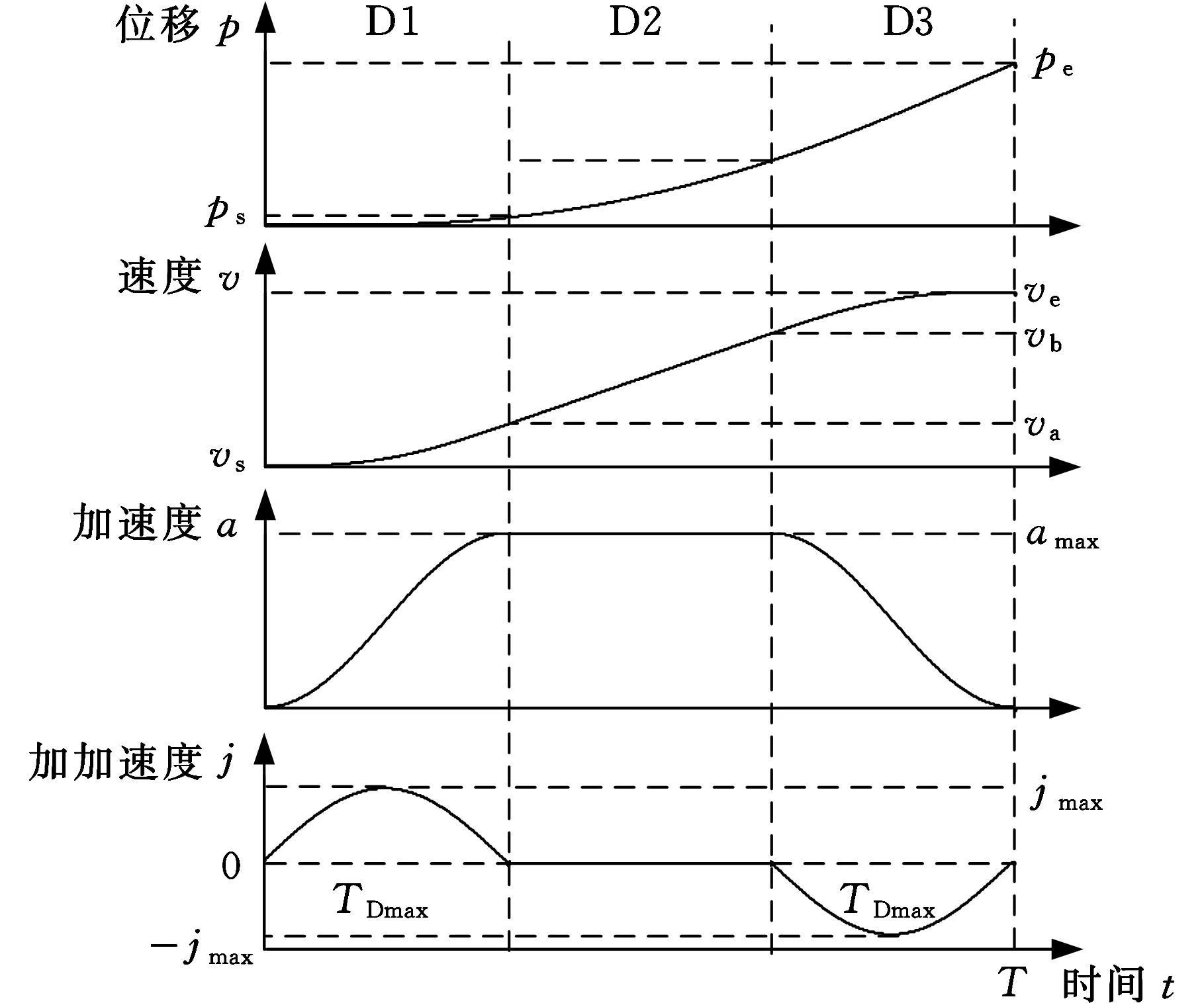
图2　正弦波加速度曲线运动规划曲线图

图2中，在(0,TDmax)时间段内，加速度曲线的正弦函数方程为

(22)

式中，t为变化时间；TDmax为加速度从0加速到最大加速度amax的时间。

对式(22)进行一阶求导，可得到加加速度的函数方程为

(23)

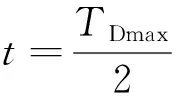
根据图2 ，可将规划轨迹划分为三段，即位移段D1(加加速段)、位移段D2(匀加速段)和位移段D3(减加速段)，可得三个轨迹段间的两个过渡点的速度分别为

(24)

根据划分的三个位移段D1、D2和D3，可得对应轨迹段的加速度函数分别为

a(t)=

(25)

由式(25)，可得对应三个轨迹段D1、D2、D3的位移量分别为

(26)

(27)

(28)

根据式(25)～式(28)，可得随时间变化的位置函数d(t)为

d(t)=

(29)

4　倍四元数的线性插值

基于倍四元数对机器人笛卡尔空间位姿的表达，使用一种利用四维空间超球面的双旋转来实现机器人笛卡尔空间曲线轨迹的插补方法进行曲线插补，该方法可实现机器人空间位姿的倍四元数插值，且其正弦波加速度曲线可保证轨迹规划曲线的C2连续，从而保证机器人在笛卡尔空间能够连续、平稳地完成指定轨迹路线[9，14-15]。

根据倍四元数的基本性质，倍四元数的G部和H部分别用单位四元数表示，在倍四元数的插值过程中可对G部和H部分别进行运算。因此，可将四元数的“球形线性插值法”(spherical linear interpolation，Slerp)运用在倍四元数中，完成倍四元数在超球面的线性插值。

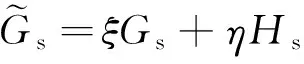
G(t)=Slerp(Gs,Ge,l(t))=

(30)

H(t)=Slerp(Hs,He,l(t))=

(31)

ωg=arccos(Gs·Ge),ωh=arccos(Hs·He)

其中，Gs·Ge、Hs·He分别为Gs与Ge、Hs与He两四元数的点积，l(t)∈[0,1]通过上述正弦波加速度曲线运动规划获得。

根据式(30)、式(31)，倍四元数的球面线性插值可表示为

(32)

f=(ωg,ωh)T

实际的插值计算过程包含倍四元数的G部和H部两个部分的球面线性插值，即式(30)和(31)，通过这两部分的单位四元数的球面线性插值完成倍四元数的球面线性插值。

5　实验仿真与验证

本文以埃夫特ER10L-C10型工业机器人为实验平台，该型号机器人适用于机床上下料、搬运、喷釉、打磨抛光等场合。采用上述倍四元数球面线性插补和正弦波加速度曲线运动速度控制对机器人末端空间轨迹位姿进行插补，利用MATLAB工具对轨迹规划进行仿真与验证。该型号工业机器人DH参数见表1。

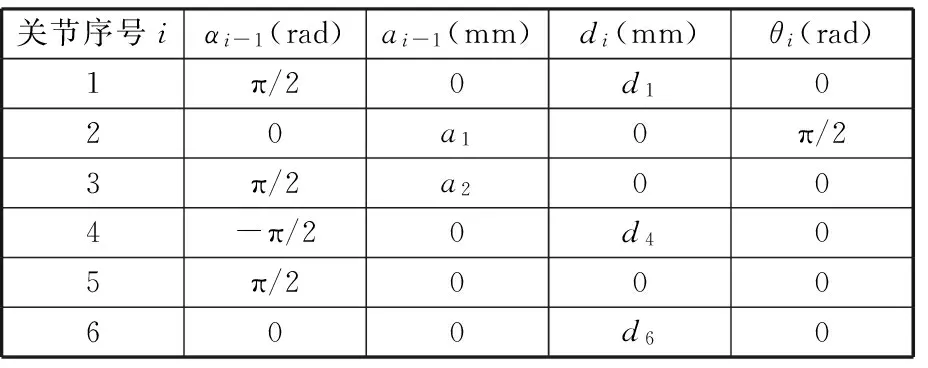
表1　ER10L-C10型机器人连杆参数

使用倍四元数球面线性插值对工业机器人任务空间的工作路线进行轨迹规划，利用Keba机器人控制器示教功能记录机器人末端执行器工作路线的起止点位姿数据，通过ER10L-C10型机器人实验平台得到路线起止点处机器人执行器末端相对于基坐标系的位姿齐次矩阵：

其中，位置数据单位为mm。

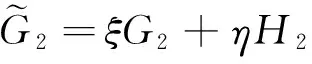
通过上述倍四元数的球面线性插补与正弦波加速度曲线的运动速度控制，可得倍四元数轨迹的位置插补仿真曲线，如图3、图4所示。图3所示为倍四元数轨迹的位置插补曲线与实际轨迹误差较大的情况下所得结果，图4所示为倍四元数轨迹的位置插补曲线与实际轨迹误差较小情况下所得结果。由图3和图4可知，使用倍四元数对机器人轨迹插补所得曲线与实际曲线间存在误差，其原因是将齐次矩阵转化为倍四元数时是近似计算的过程，整个过程有一定的精度损失。但误差大小是可控的，通过采用不同的数值计算精度δ、机器人工作空间的最大边界L等参数，计算误差可任意改变。

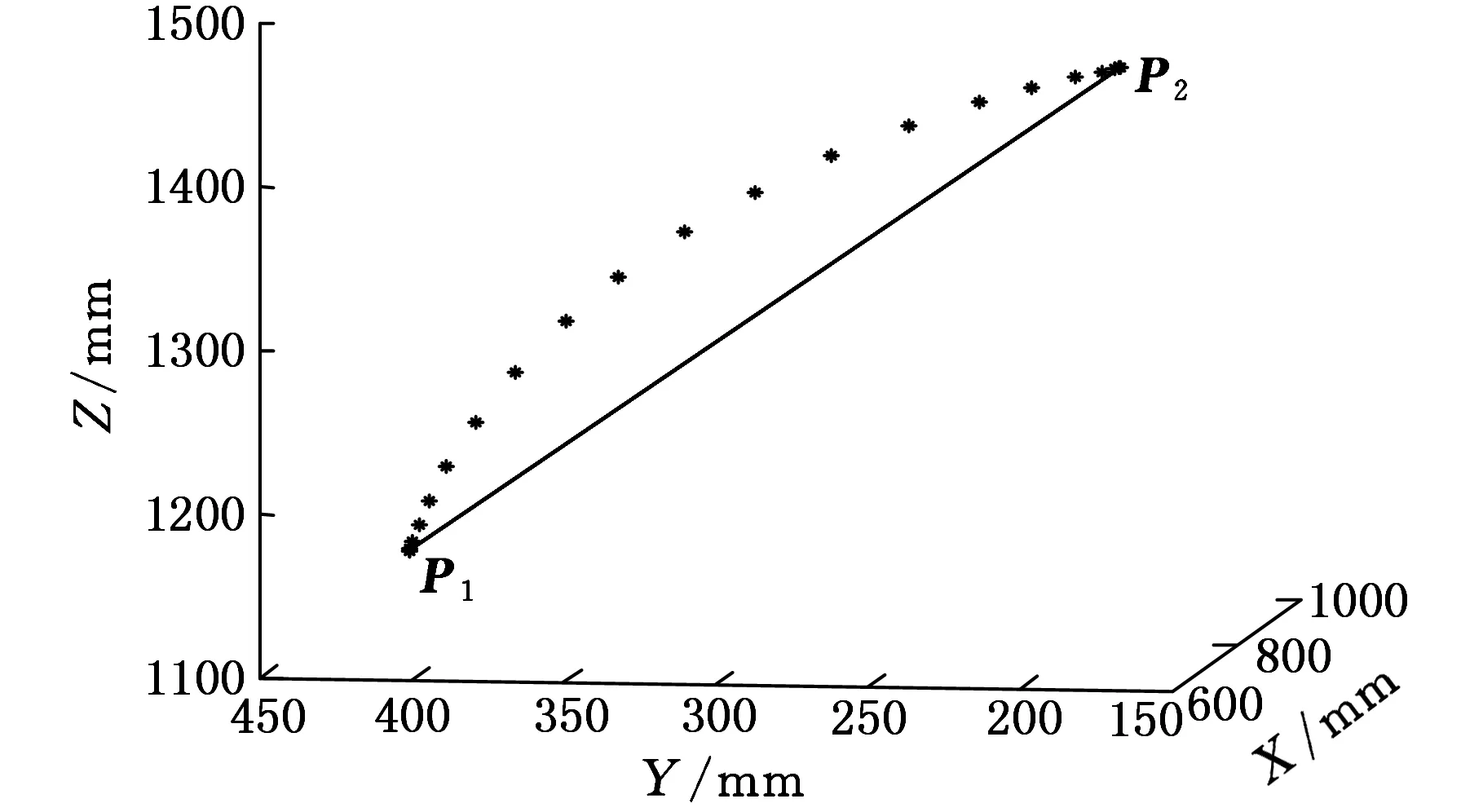
图3　倍四元数法位置曲线1

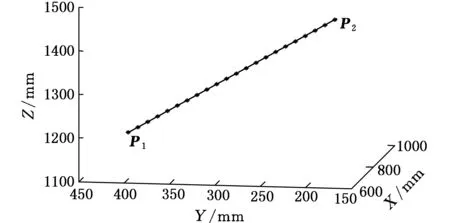
图4　倍四元数法位置曲线2

通过倍四元数球面线性插补获得轨迹位置插补点的同时，可获得相应的姿态插补数据，将其转化为超球面的旋转矢量表示，如图5所示。可见，四维空间超球面的旋转矢量过渡平滑。

图5　倍四元数姿态变化曲线

由式(6)，将实时插补所得的旋转四元数Q转化为旋转矩阵R，并经滚动-俯仰-偏航角(roll-pitch-yaw,RPY)姿态表示方法的逆变换可得绕X、Y、Z轴旋转的角度α、β、γ(图6)。可见，在笛卡尔坐标系中α、β、γ角的插补轨迹连续且平滑，说明利用倍四元数对机器人任务空间的姿态进行描述是可行的。

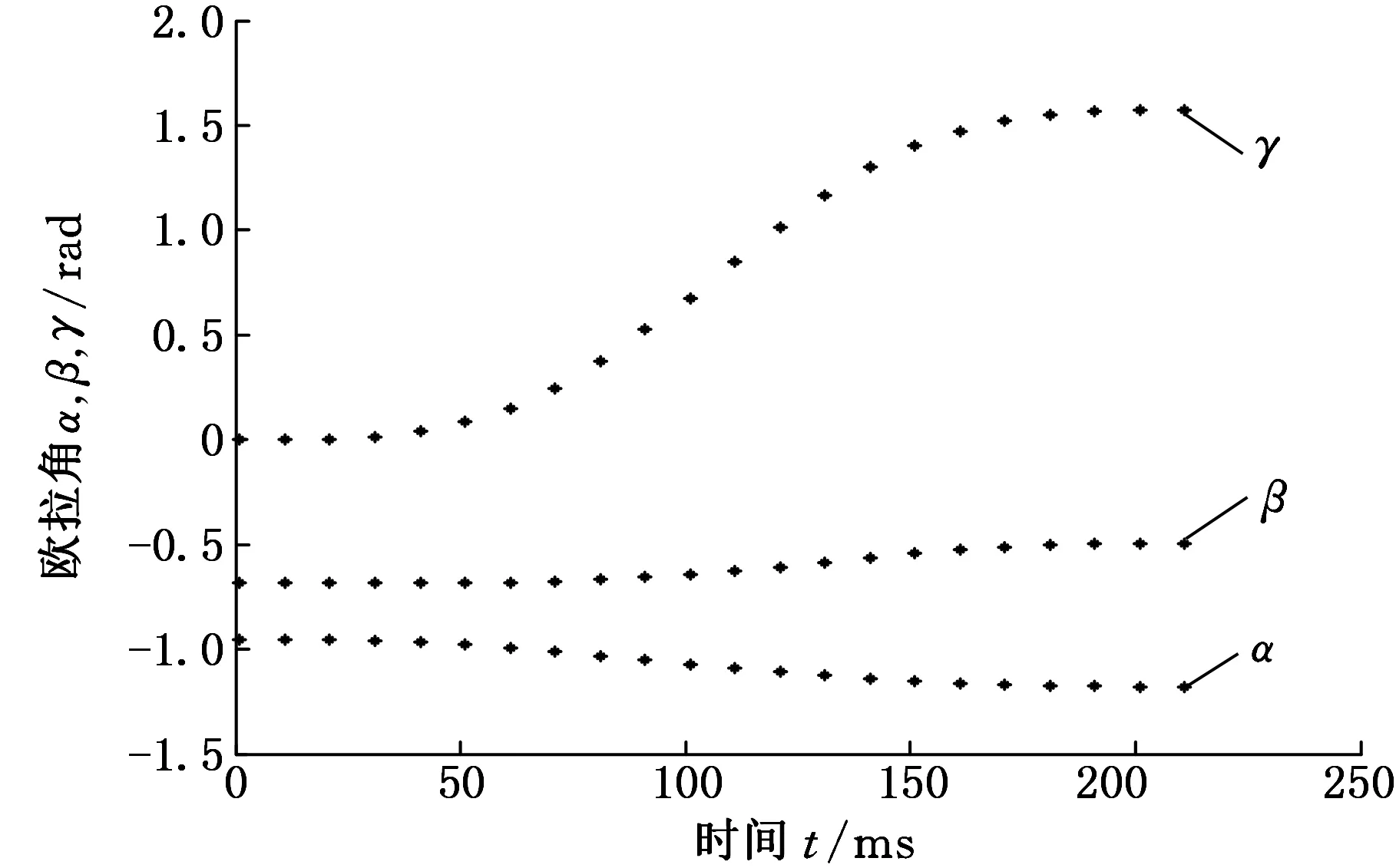
图6　RPY逆变换旋转角轨迹曲线

为显示倍四元数插补过程中笛卡尔空间的位姿变化，由式(12)、式(13)将倍四元数转化为旋转四元数和位置矩阵，其旋转角度ψ的变化曲线如图7所示，ψ的平滑连续变化验证了倍四元数进行轨迹规划的有效性。

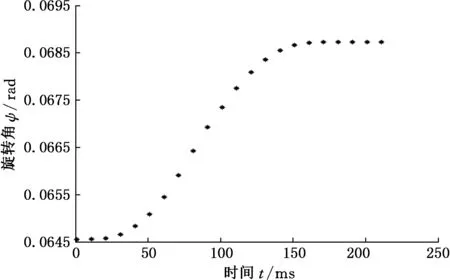
图7　旋转角度ψ的插补曲线

使用倍四元数进行轨迹规划的过程中，采用了正弦波加速度曲线升降速控制，其运动规划曲线如图8所示。由图8可见，加加速度曲线、加速度曲线、速度曲线以及位移曲线均符合机器人轨迹规划的要求，其加速度曲线平滑连续，保证了C2连续，为机器人位置与姿态插补提供了平滑连续的速度控制。

图8　运动规划曲线

6　结语

将机器人任务空间的齐次变换矩阵分解为旋转与平移两部分，通过变换得到倍四元数的表达形式，然后使用在四维空间超球面旋转的倍四元数，对机器人运动轨迹进行球面线性插补。虽然整个计算过程中存在精度损失，但通过采用不同的数值计算精度和控制参数，计算误差可进行调节。该方法为机器人轨迹规划提供了一种新的位姿规划的解决方案，具有计算速度快、鲁棒性强的特点；同时，针对轨迹的平滑性要求，采用正弦波加速度曲线进行升降速控制，能够保证C2连续，且计算量相对较小，较好地满足了机器人控制的实时性要求。测试和仿真结果证明了算法的有效性。

[1]CraigJJ.机器人学导论[M].牟超，译.北京：机械工业出版社,2012.

[2]DamEB,KochM,LillholmM.Quaternions,InterpolationandAnimation[R].Copenhagen，Denmark：UniversityofCopenhagen,1998.

[3]季晨. 工业机器人姿态规划及轨迹优化研究[D].哈尔滨：哈尔滨工业大学,2013.

[4]孙斌,常晓明,段晋军.基于四元数的机械臂平滑姿态规划与仿真[J].机械科学与技术,2015(1):56-59.

SunBin,ChangXiaoming,DuanJinjun.SmoothOrientationPlanningandSimulationofManipulatorBasedonQuaternion[J].MechanicalScienceandTechnologyforAerospaceEngineering, 2015(1):56-59.

[5]刘松国,朱世强,王宣银,等. 基于四元数和B样条的机械手平滑姿态规划器[J]. 浙江大学学报(工学版),2009,43(7):1192-1196.

LiuSongguo,ZhuShiqiang,WangXuanyin,etal.SmoothOrientationPlannerforManipulatorsBasedonQuaternionandB-spline[J].JournalofZhejiangUniversity(EngineeringScience),2009,43(7):1192-1196.

[6]高亚军.六自由度机器人平滑轨迹规划与控仿一体化系统研究[D].杭州：浙江工业大学,2014.

[7]王健. 6R串联机器人轨迹规划算法研究[D].北京：北方工业大学,2014.

[8]乔曙光,廖启征,黄昔光. 倍四元数及其在串联机构运动分析中的应用[J]. 机械设计与制造,2008(2):36-38.

QiaoShuguang,LiaoQizheng,HuangXiguang.ApplicationofDoubleQuaternionsinInverseSolvingofSerialMechanisms[J].MachineryDesign&Manufacture, 2008(2):36-38.

[9]廖啟征. 机构运动学建模的倍四元数法[J]. 北京工业大学学报,2015,41(11):1611-1619.

LiaoQizheng.KinematicModelingofMechanismsSsingDoubleQuaternion[J].JournalofBeijingUniversityofTechnology,2015,41(11):1611-1619.

[10]马艳红,胡军. 姿态四元数相关问题[J]. 空间控制技术与应用,2008,34(3):55-60.

MaYanhong,HuJun.OnAttitudeQuaternion[J].AerospaceControlandApplication, 2008,34(3):55-60.

[11]张劲夫,蔡泰信. 对偶四元数及其在刚体定位中的应用[J]. 黄淮学刊(自然科学版),1993,9(增刊4):27-30.

ZhangJinfu,CaiTaixin.DualQuaternionandItsApplicationinRigidPositioning[J].HuanghuaiJournal(NaturalScience),1993,9(S4):27-30.

[12]刘鹏飞,杨孟兴,宋科,等. ‘S’型加减速曲线在机器人轨迹插补算法中的应用研究[J]. 制造业自动化,2012,34(20):4-8.

LiuPengfei,YangMengxing,SongKe,etal.TheStudyofS-curve’sApplicationonManipulator’sTrajectoryInterpolationAlgorithm[J].ManufacturingAutomation, 2012,34(20):4-8.

[13]林仕高,刘晓麟,欧元贤. 机械手笛卡尔空间轨迹规划研究[J]. 机械设计与制造,2013(3):49-52.

LinShigao,LiuXiaolin,OuYuanxian.TheStudyofTrajectoryPlanningofManipulatorinCartesianSpace[J].MachineryDesign&Manufacture, 2013(3):49-52.

[14]杜滨. 全方位移动机械臂协调规划与控制[D].北京：北京工业大学,2013.

[15]张红强. 工业机器人时间最优轨迹规划[D].长沙：湖南大学,2004.

(编辑苏卫国)

Research on Trajectory Planning of Industrial Robots with Double Quaternion

Li HongshengWang YunheHuang JiacaiShi Xinxin

Nanjing Institute of Technology,Nanjing,211167

For the curve smoothness and real-time requirements of industrial robot trajectories in cartesian space, the paper represented hyperspheres rotation quaternion of robot trajectory spherical linear interpolation, combined with the algorithm of sinusoidal acceleration curve lifting velocity to control the trajectory planning. It provides a new solution of position and pose planning. Finally, simulations were performed in six joints handling robot control system platform, then to prove the validity of the algorithm solution.

industrial robot; double quaternion; sinusoidal acceleration curve; trajectory planning

2015-12-08

江苏省科技支撑计划资助项目(BE2014025)

TP242.2

10.3969/j.issn.1004-132X.2016.20.003

李宏胜，男，1966年生。南京工程学院自动化学院教授。研究方向为数控技术、高性能伺服驱动、机器人控制、智能控制。发表论文70余篇。汪允鹤(通信作者)，男，1990年生。南京工程学院自动化学院硕士研究生。黄家才，男，1977年生。南京工程学院自动化学院教授。施昕昕，女，1985年生。南京工程学院自动化学院副教授。