基于FDM成型工艺的适应性分层方法研究

姜化凯　于文强

(山东理工大学机械工程学院，山东 淄博 255000)



基于FDM成型工艺的适应性分层方法研究

姜化凯于文强

(山东理工大学机械工程学院，山东 淄博 255000)

为了兼顾FDM快速成型工艺的精度和效率，提出基于STL模型的适应性分层方法。从FDM快速成型工艺的特殊性和STL文件的数据结构特点出发，提出了不同FDM设备的最佳适应性层厚范围的理论计算方法，并针对STL格式文件中三角形面之间相互孤立、相邻三角形信息冗余度高和相邻两层之间信息继承性高的特点，采用了按三角形高度分组并建立自由三角形表及其动态拓扑结构求闭环轮廓的方法，适应性层厚根据同一面上相邻两层上的闭环轮廓长度差值比率来确定。结果表明，在提高成型精度的前提下，分层效率同时得到保证。

FDM；适应性分层；自由三角形表；动态拓扑

熔融沉积成型(FDM)的分层方法有等厚度和适应性分层两种[1-2]。等厚度分层存在精度失效率这一现象；适应性分层在分层方向上，能够根据零件的表面轮廓形状自动地改变分层厚度，兼顾了成型效率和精度。在熔融沉积成型工艺过程中，热塑性材料通过喷头时被加热挤压成熔融状态的细丝，喷头按照CAD模型分层后的二维层面上的信息运动，沿分层方向层层堆积成型。因此，CAD模型的分层效果直接决定了零件成型时的精度和效率。CAD模型经过表面三角离散化后就形成了FDM快速成型工艺中最常用的STL格式文件，它表现为一组无序的三角形集合。基于STL模型的适应性分层效率主要取决于：搜索与分层平面相交三角形、闭环轮廓和适应性层厚计算等方面。

目前搜索相交三角形主要有基于全局拓扑信息和三角形几何特征两种[3-4]，前者建立全局拓扑关系相当耗时，后者需要对三角形在分层方向上进行高低位置排序且求出的交点还需排序；适应性层厚的计算目前主要有相邻两层面积差比率法、表面曲率法和顶尖误差法，计算闭环轮廓面积采用三角形分割耗时多而用扫描线求解精度不高，曲率求解困难且一层上要计算多点的曲率，顶尖高度计算法公式多而复杂[5-7]。本文计算了理论上FDM快速成型的适应性分层过程中的最大和最小层厚，采用最大层厚值将所有三角形分组并建立自由三角形表减少三角形的搜索次数，适应性层厚计算采用相邻两层闭环轮廓长度差比率的方法，有效提高了分层效率。

1　最大和最小层厚的计算

受成型设备自身的条件限制，不同的FDM成型设备可允许的最大和最小分层厚度不同，具体表现为喷嘴直径的不同和所用耗材的不同。耗材经送丝机构进入喷头被加热至熔融态，以熔融态细丝形式从喷嘴处挤出落到加工层面上。细丝从喷嘴处被挤出那一刻到其上下左右都有细丝覆盖时，细丝的横截面形状由最初的圆形变成椭圆形最后受到力的挤压作用变形成带圆角的矩形。截面形状变化过程如图1所示。

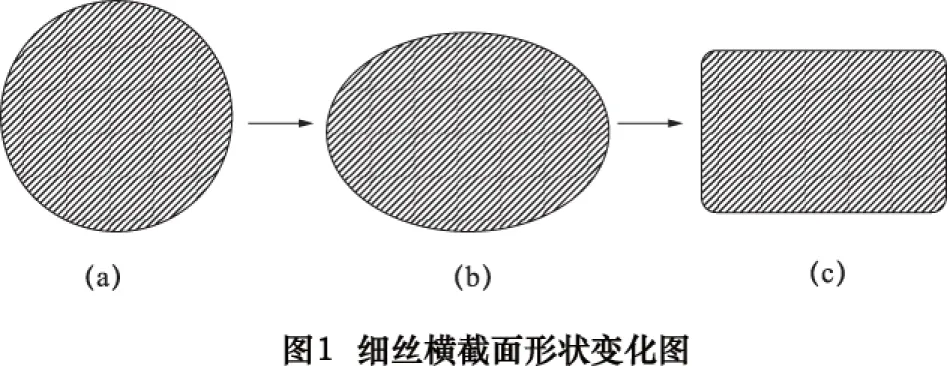
聚乳酸(PLA)材料是由可再生植物资源中的淀粉制成的生物降解材料，成型温度200 ℃左右、无刺鼻性气味、收缩率低。在实际成型中细丝在横截面形状的变化过程中截面面积变化不大，在这里假定图1所示的各过程中截面面积相等来计算层厚范围，式(1)是面积计算公式，式(2)是计算截面高度的公式。

(1)

(2)

式中：d是喷嘴直径；β是PLA材料的面热膨胀系数；Δt是温差；a、b是椭圆长、短半轴长度；a1、b1是圆角矩形的长和高(厚)。

PLA材料在205 ℃的成型温度下线热膨胀系数α=260×10-6[8]。在测量PLA材料线热膨胀系数时试体为一长方体 ，边长为L1，底面积为S1。当温度由T1升到T2时，长度变为L2，底面积变为S2，下面是由线膨胀系数α推导面膨胀系数β的计算过程。

(3)

(4)

由于式(4)中线膨胀系数较小，可忽略高阶无穷小，取一阶近似：β=2α。已知横截面的最佳长高比a1/b1的范围在3.5到6之间[9]，即3.5≤a1/b1≤6，Δt取200 ℃，当a1/b1的值取3.5时，可以求得最大层厚值。

(5)

当a1/b1的值取6时，可以求得最小层厚值。

(6)

由式(5)、(6)可知，FDM设备在使用PLA耗材时不同的喷嘴直径d对应的理论最佳层厚范围是：[0.380 1d,0.497 7d]。

2　最大层厚值分组分层算法

STL格式文件最先由3D System公司发明，它是由充满模型表面的无序三角形组成，相邻两个三角形共用两个顶点，每个顶点至少被3个三角形共用，其中每个三角形又包括3个顶点坐标和右手法则定义下的朝模型外侧的法矢量，这就容易在分层过程中产生冗余数据[10-11]。

由于STL模型上所有的三角形之间没有几何拓扑关系，所以能否高效地寻找与分层平面相交的所有三角形是提升分层效率的关键。首先，按三角形的高低位置将所有的三角形分组，大体确定三角形位置；其次，建立自由三角形表直接得到与分层平面相交的三角形；最后，把相交三角形的数据信息建立链表分类处理，创建动态拓扑结构得到闭环轮廓。

2.1三角形分组规则

在STL文件中，每个三角形都存储有3个顶点的坐标值，在分层方向上把3个顶点中高度最小点的Z坐标值称之为该三角形的高度。根据三角形的高度不同，将所有的三角形在Z方向上由低到高分组，分组按照FDM设备允许的最大加工层厚为每组的长度。这样做是为了使每个三角形都有精确的分组位置，在寻找与当前分层平面相交的三角形时就可以减小搜索范围，同时也避免三角形被重复搜索计算而尽可能地减少冗余数据。

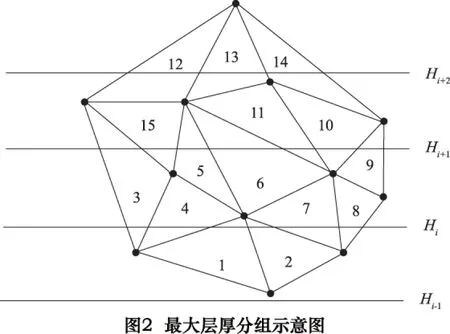
如图2所示，水平的直线就是分组界限，每两条平行直线之间为一组且距离就是最大层厚值的大小。每个三角形的最低点的Z坐标值代表它的高度，如果一个三角形的高度出现在高度(Hi-1～Hi)这个范围内，那么该三角形属于第i组内。这样的分组方法使得出现在组内的每个三角形都是首次出现的三角形。表1是图2所示的STL模型局部三角形分组情况表。

表1三角形分组

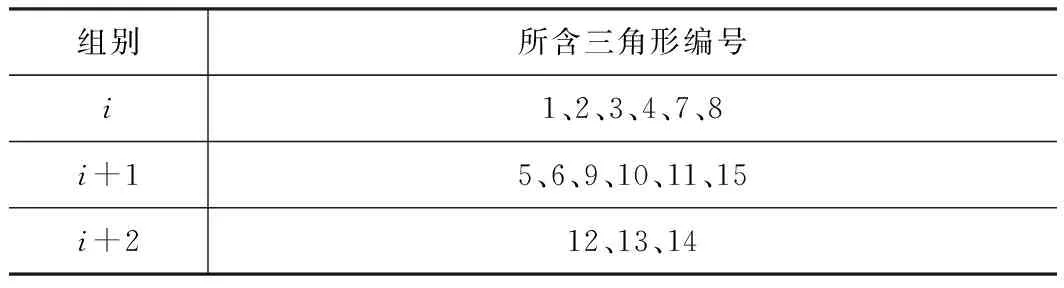
组别所含三角形编号i1、2、3、4、7、8i+15、6、9、10、11、15i+212、13、14

2.2自由三角表的建立

由于STL模型上某些三角形会跨越多个组别，如果只搜索分层平面所处组别中的三角形就会丢失数据使精度下降甚至出错[12]。这就需要在搜索第一层上的三角形时建立一个对象来储存与当前层相交的三角形，当搜索下一层面上的相交三角形时，除搜索新加入的组别中的三角形还要继续沿用上一层上的相交三角形。这个对象就是自由三角形表，自由三角形表就是与当前层所有相交的三角形的集合，是不断更新的。这些三角形包括：上一层中的相交三角形除去那些最高点坐标小于当前分层平面的和当前分层平面所处分组中那些三角形高度大于分层平面高度的。

适应性分层首先以最大加工厚度对第一层进行分层，由于分层平面处于第一组内，把第一组内的三角形全部存入自由三角形表。第一层分层结束后进行下一层上的分层工作，与第二层上的分层平面相交的三角形一部分来自分层平面所处的组内的三角形，还有一部分可能来自上一层上的自由三角形表中，舍去上一层自由三角形表中那些三角形的最高点的Z坐标值小于分层平面高度的三角形和本组中三角形高度大于分层平面高度的三角形，其中本组中不符合条件的三角形存入下一组。把这两部分的三角形重新赋给新的自由三角形表，即为第二层上的自由三角形表。把第i层上的自由三角形表用Ti表示，该层所处的组别是Gi，那么当前层上的自由三角形表就可以表示为：

Ti=Ti-1-F+Gi-F′

(7)

式中：F代表上一层的自由三角形表中位于分层平面下方的三角形；F′表示当前组别中高度值大于分层平面高度的那些三角形。

自由三角形表随着分层平面的升高不断有新的三角形加入也有不符合条件的三角形被删除，自由三角形表的存在大大减少了分层平面与三角形位置关系的判断次数。

2.3动态拓扑结构创建

动态拓扑创建的数据结构有3类，分别为点(Vertex)、边(Edge)和面(Facet)。建立这三类数据结构的双向循环链表：点表(VertexList)、边表(EdgeList)、面表(FacetList)。

双向循环链表节点结构体定义：

typedef struct NameList

{

DataType data;

struct NameList *next;

struct NameList *prev;

}

每个节点结构体内定义了指向前后节点的前驱指针*prev、后继指针*next和数据信息(data)。点表储存每个点的3个坐标(floatv1,v2,v3)和索引号(VIndex)，边表储存每条边的两个端点的索引号(EVIndex)和共享该边的两个三角形的索引号(EFIndex)，面表储存组成三角形三边的索引号(EIndex)和该三角形的索引号(FIndex)。图3是双向循环链表的结构图。下面是动态拓扑结构的构建过程。

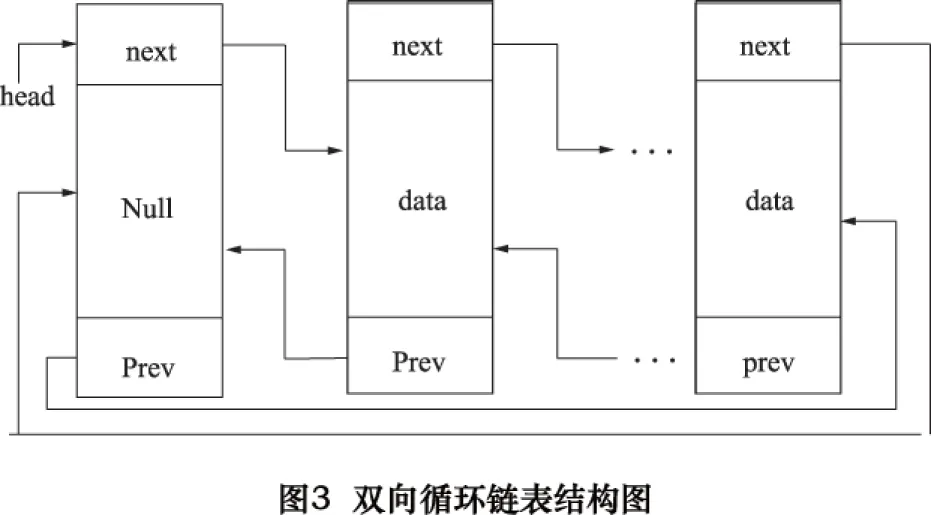
(1)首先建立第一层上的拓扑关系，从第一层的自由三角形表中任选一个三角形，将三角形的三点、三边及面赋初始索引值并将相应数据存入三个链表中。

(2)搜索下一个三角形，若三角形的点与已存在的点表中有重复，则把点表中的索引值赋给该三角形中共享该点的两条边的索引EVIndex；若没有，则表示该点是一个新出现的点，则给该点赋新索引值并添加到VertexList中，同时将新索引值赋给共享该点的两条边的EVIndex。依次遍历该三角形的三点。

(3)搜索三边中的一边，判断边表中有无该边。若有则将边表中的边索引号赋给面表中该三角形的FEIndex1并把该三角形面表的索引号赋给EFIndex2；若没有则表示该边是新出现的边，则给该边赋新索引值并添加至EdgeList中，同时将该三角形的面索引号赋给该边的EFIndex1。依次遍历该三角形中的三边。

(4)读取该层上自由三角形表中的所有三角形，至此该层上的拓扑结构完毕。

如果下一层的自由三角形表无新三角形加入，则沿用上一层上的拓扑结构。若有更新则按照上面的方法，将新增的三角形的3类数据进行相应的链表更新，那些已被判定为不与分层平面相交的三角形将其从FacetList链表中删除。

表2拓扑结构

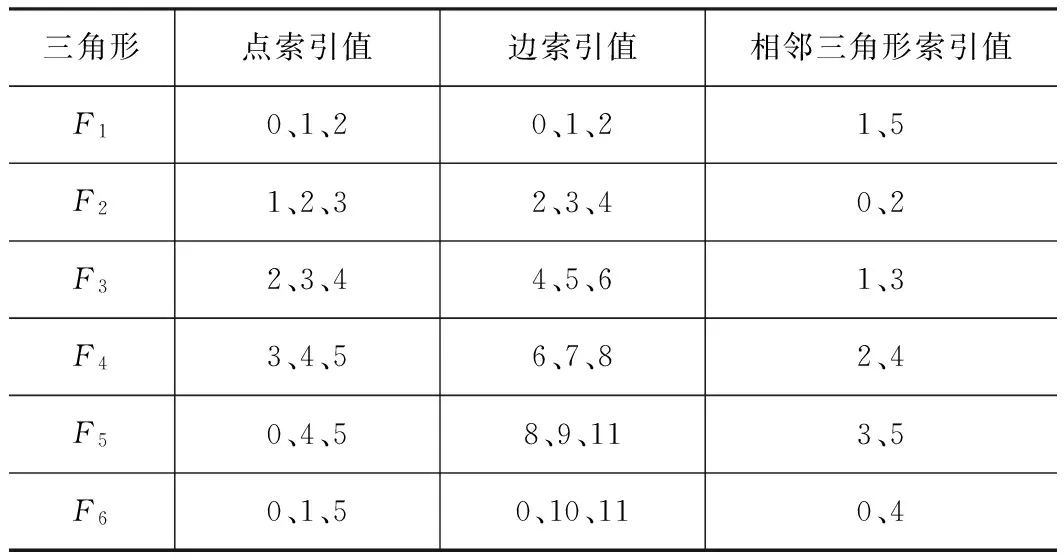
三角形点索引值边索引值相邻三角形索引值F10、1、20、1、21、5F21、2、32、3、40、2F32、3、44、5、61、3F43、4、56、7、82、4F50、4、58、9、113、5F60、1、50、10、110、4

图4表示的是某层上的能够闭合的三角形环结构，表2表示的是图4结构的拓扑关系，其中每类数据的索引值从0开始递增，即V1、E1和F1的索引值都为0。

3　适应性分层厚度

3.1闭环轮廓的计算

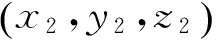
(8)

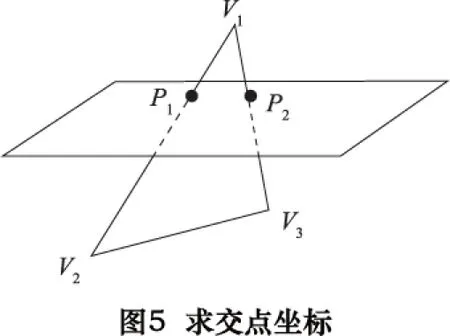
按照拓扑信息依次计算相邻三角形各边与分层平面的交点，直至首尾相接完成一个封闭环。有些层面上可能有多个闭环轮廓，继续搜索自由三角形表中剩余的三角形求出所有的闭环轮廓为止。

3.2分层厚度计算

在第1节中计算了理论上的PLA材料在FDM成型工艺中设备所允许的最小和最大加工厚度，适应性分层就是在这个加工范围之内根据表面形状变化自动地计算分层厚度，以减小阶梯误差。目前适应性层厚计算的方法主要有基于模型表面曲率的方法，该方法是通过计算模型表面轮廓上各点的曲率值来确定分层厚度，在轮廓上的点的曲率计算是比较困难的，且一个层面上要对多个点进行计算这就加大了算法的复杂程度；基于面积变化率的方法是比较相邻两层面积差值大小进而改变分层厚度，在求面积的时候如果采用三角形分割截面图形那么计算量会很大，如果用扫描线求面积则精度难以保证；基于顶尖高度误差的计算方法计算公式多而繁琐。所以提出基于同一表面相邻两层之间闭环轮廓长度差值比率的判断方法来计算当前分层层厚。

由于在求闭环轮廓的时候已经建立了动态拓扑结构，且求交后得到的点是有序的，因此就可以利用两点之间的距离公式计算出两点之间的距离，把相邻的所有的线段长度相加就得到了闭环轮廓的长度。根据相邻两层在同一个表面上的闭环轮廓的长度差值比率来控制分层厚度。给定相邻两层最大长度差值比率为[η]，当比率小于[η]则沿用最大层厚，否则将减小分层厚度。

(9)

(10)

式(9)是闭环轮廓的长度计算公式，i代表的是有动态拓扑结构求交后的有序点的序号；式(10)是相邻两层之间闭环轮廓长度的差值比率，其中Li代表第i层上的闭环轮廓长度。

基于STL格式文件的FDM成型工艺的适应性分层方法步骤如下：

(1)读取STL数据文件，获取模型的高度值。

(2)借助最大层厚值将模型上的所有三角形分组。

(3)建立自由三角形表并构建其动态拓扑结构。

(4)分层平面与三角形求交点，得出当前层闭环轮廓并计算长度。

(5)判断当前层闭环轮廓与上一层长度差值比率并与[η]比较，若大于给定值则改变层厚并返回步骤(3)，否则继续步骤(6)。

(6)当前层上成型。

(7)判断分层平面的高度是否大于模型高度，若大于则成型结束，否则返回步骤(3)。

本文算法已经通过VC++6.0和OpenGL实现。图6是1个以STL格式表示的CAD模型[13]，模型含960个三角形面，482个顶点，1 440条边，模型高度28.27 mm，表面积约24.913 3 cm2，体积11.645 9 cm3，FDM设备喷嘴直径0.5 mm。图7～9和表3是对图6模型进行不同分层情况的比较。

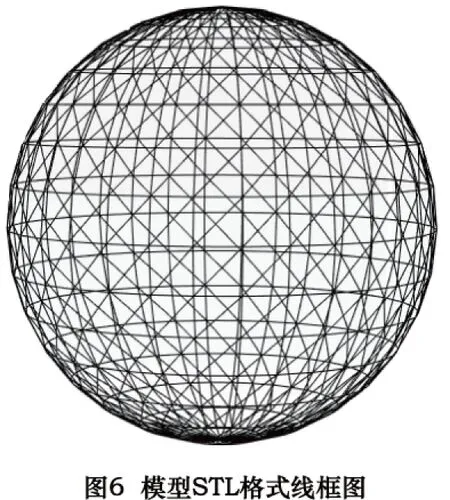
表3不同分层方式对比

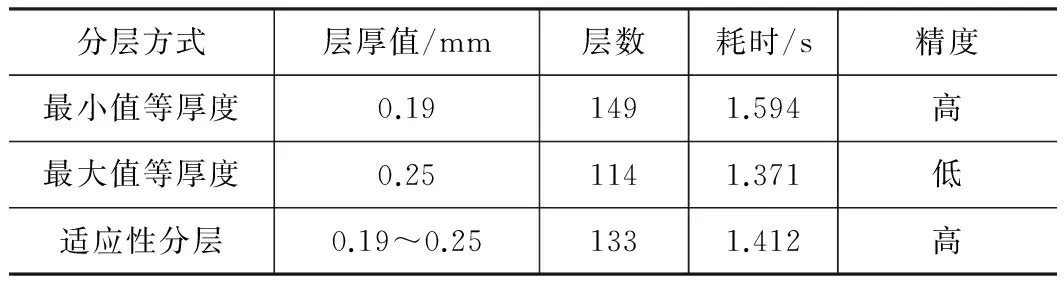
分层方式层厚值/mm层数耗时/s精度最小值等厚度0.191491.594高最大值等厚度0.251141.371低适应性分层0.19～0.251331.412高

4　结语

通过截面形状变化规律结合喷嘴直径以及耗材膨胀系数求得最大和最小层厚，为FDM后续适应性分层提供了理论取值范围。

以最大分层厚度值对STL模型上的三角形分组并建立自由三角形表和其动态拓扑关系，自由表的建立减少了分层平面与相交三角形位置关系判断次数，动态拓扑结构直接获得了有序交点提高了分层效率。

相邻闭环轮廓长度差值比率的层厚计算方法，直接沿用了动态拓扑结构求交后获得的有序交点，利用该方法确定当前层加工层厚简单有效。

[1]赵吉宾, 刘伟军. 快速成形技术中基于STL模型的分层算法研究[J]. 应用基础与工程科学学报, 2008, 16(2):224-233.

[2]张嘉易, 刘伟军, 王天然. 三维模型的适应性切片方法研究[J]. 中国机械工程, 2003, 14(9):750-752.

[3]谢存禧, 李仲阳, 成晓阳. STL文件毗邻关系的建立与切片算法研究[J]. 华南理工大学学报, 2000, 28(3):33-38.

[4]胡德洲, 李占利, 李涤尘,等. 基于STL模型几何特征分类的快速分层处理算法研究[J]. 西安交通大学学报, 2000, 34(1):37-40.

[5]毕晓亮, 朱昌明, 侯丽雅.快速成型中的自适应切片方法研究[J]. 计算机应用研究,2002, 19(4):21-22.

[6]周岩, 卢清萍, 郭戈,等.快速原型技术(RP)中的自适应分层[J]. 昆明理工大学学报:自然科学版,2001,26(4):51-54.

[7]黎步松, 周钢, 王从军,等. 基于STL文件格式的实体分割算法研究与实现[J]. 华中科技大学学报:自然科学版, 2002, 30(3):40-42.

[8]李明珠. 纳米纤维素/聚乳酸复合材料的制备与研究[J].塑料工业,2012,40(7):17-20.

[9]吴大鸣 刘颖 李晓林. 精密挤出成型原理及技术[M].北京：化学工业出版社, 2004.

[10]Szilvi-Nagy M, si, Gy. Analysis of STL files[J]. Mathematical & Computer Modelling, 2003, 38(7-9):945-960.

[11]赵保军, 汪苏, 陈五一. STL数据模型的快速切片算法[J]. 北京航空航天大学学报, 2004, 30(4):329-333.

[12]周华民, 成学文, 刘芬,等. STL文件错误的修复算法研究[J]. 计算机辅助设计与图形学学报, 2005, 17(4):761-767.

[13]陈太喜, 方亮, 刘艳伟,等. 基于OpenGL的STL数据模型建模方法[J]. 机床与液压, 2009, 37(3):155-158.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Research on the method of adaptive slicing based on FDM

JIANG Huakai, YU Wenqiang

(School of Mechanical Engineering，Shandong University of Technology，Zibo 255000,CHN)

In order to take into account the accuracy and efficiency of the FDM rapid prototyping, an adaptive slicing method based on STL model is proposed. Starting from the special characteristics of FDM rapid prototyping and the characteristics of the data structure of STL file, a theoretical calculation method for the adaptive slicing thickness range of different FDM devices is proposed. Based on the STL format file, the high degree of information redundancy between adjacent two layers is high and the information inheritance between the adjacent triangles is high. Proposed establish free triangle table and its dynamic topology structure to solve the closed loop profile. The thickness of slicing maximum and minimum of the FDM device are calculated, and the adaptive slicing thickness is controlled by the ratio of the length of the closed loop profile of two adjacent layers on the same surface. The results show that, under the premise of improving the molding precision, the efficiency of the delamination can be guaranteed.

FDM; adaptive slicing; free triangle table; dynamic topology

TP391

A

10.19287/j.cnki.1005-2402.2016.10.006

姜化凯，男，1991年生，硕士，研究方向为快速成型、增材制造技术。

(编辑陈纲)

2016-06-21)

161010