电力市场中Bertrand模型的复杂性分析
王国栋,卓春英
(重庆水利电力职业技术学院 基础教学部,重庆 402160)
电力市场中Bertrand模型的复杂性分析
王国栋,卓春英
(重庆水利电力职业技术学院 基础教学部,重庆 402160)
为了模拟电力市场中发电商采取不同策略的博弈行为,在考虑输电网约束条件下将动态Bertrand博弈模型引入电力市场,建立有限理性条件下的投资模型,并运用有限理性法和不完全信息法实现了投资模型由静态到动态的转化过程,求解了动态模型的价格均衡,并分析了均衡点的稳定状态,给出其经济解释。
电力市场;Bertrand模型;有限理性法;不完全信息法
0 引言
发电商、用户以及庞大的输电网组成了十分复杂的电力市场,追求自身利益最大化是各市场成员的唯一目标,最大利润点也是其运动方向.在市场供需关系和电价的调控下,发电商不断调整自己的发电量,用户不断改变自己的用电量,最终实现电力系统资源的优化配置[1]。电力市场的动态演化,即发电量、用电量与电价等随时间演化的行为包含了市场中的各种信息,分析并掌握电力市场的动态行为,有助于市场管理者制定有效的市场规则来合理运营电力市场,也有助于市场参与者制定有效的交易计划来获得最大的经济利润[2-3]。杨洪明[4]等在考虑输电网约束下对有限理性古诺博弈的动态演化进行了分析,传统的Cournot模型参与博弈的双方是以产量作为决策,而Bertrand模型参与博弈的双方是以价格为决策变量,会导致每个企业的定价采用完全竞争情况下的价格,即所谓的边际成本定价法。近年来,有限理性法与Puu的不完全信息法也被用来研究企业处于垄断市场的分析,有限理性的企业是基于离散时间和边际利润的局部估计来实现其生产策略。而Puu的不完全信息法[5]最大的特点是现实性,在预测一个企业的产量时不需要知道利润函数在当前时间步骤的具体形式,而只需要知道利润和价格在过去两个时间步骤的数值。现阶段对Bertrand模型的研究较多,大多集中在静态模型到动态模型的转化以及模型均衡点的求解,姚洪兴[6]等在动态Bertrand模型的复杂性现象与混沌控制一文中对模型进行了混沌控制,但只考虑到需求函数与成本函数为线性的,考虑到电力市场的复杂性,本文将成本函数定义为非线性,对模型实现由静态到动态的转化,并且对模型的均衡点进行分析。
1 模型的建立与分析
假设市场由两个区域市场组成,记发电商为A,B,他们通过一条输电线路连接,线路的最大传输功率为k ,且满足如下要求:
-2k≤q1-q2≤2k。
(2)当输电线出现阻塞时,且线路上传输功率为k时,电价函数为:
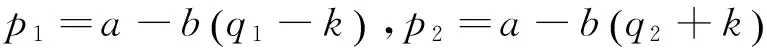
当线路上传输功率为-k时,电价函数为:

(3)于是在考虑输电网约束的情况下,电力市场的电价函数为:
(1)
和
(2)
2 动态Bertrand模型分析
(1)有限理性方法是使用基于局部评价调整机制的边际利润,描述动态调整机制的动力系统如下:
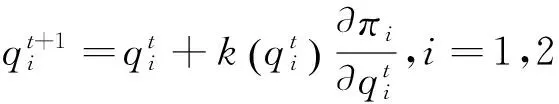
(3)
发电商A,B的利润函数为:

因此,发电商A,B组成动力系统:

(4)
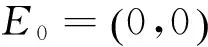
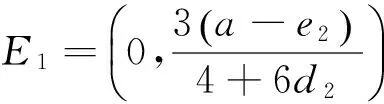

当a>e1,a>e2时(可以保证平衡发电量为正),均衡点E1,E2被定义为垄断平衡点。为了得到更多关于两个垄断点的信息,现进行如下分析与证明。
命题1如果a>e1,a>e2,则有(i)均衡点E0为排斥节点;(ii)垄断点E1,E2是不稳定均衡点;(iii)E3在满足一定条件下为局部渐进稳定点。
证明:基于标准的特征值分析,在点E0处的Jacobian矩阵为:

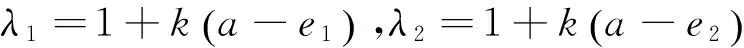
在E1处的Jacobian矩阵为:
特征值:


因为a>e1,a>e2,所以系统稳定的条件为:


进一步研究稳定点E3的稳定性,在E3处的Jacobian矩阵为:
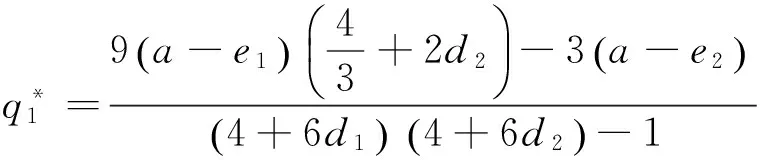
由非线性系统稳定条件可得到:


图1 变量q1、q2随k值变化的分岔图
当系数k,a,d1,d2,e1,e2满足上述条件①②时,系统处于稳定状态,当系数k,a,d1,d2,e1,e2超出条件①②时,系统会进入混沌状态,由于上述方程难于求解,下面将用软件来模拟系统的发展过程。
当a=4,d1=d2=0,e1=e2=0.5,0 (2)采用Puu的不完全信息法来研究Bertrand模型[7-8],此方法中发电商的发电量可以表达为; (5) (6) 证明:s0的证明同命题1,这里略去证明。为了讨论均衡点s1的局部稳定性,给出它的Jacobian矩阵,如下: 本文为了模拟电力市场中发电商采取不同策略的博弈行为,在考虑输电网约束条件下将动态Bertrand博弈模型引入电力市场,由于电力市场的复杂性,考虑成本函数为非线性,并通过有限理性方法与Puu的不完全信息方法来描述这两个模型,从而为发电商做出决策。在不完全信息下,发电商通过过去两次的发电量来决定未来的发电量,而在其他方法中,未来的发电量取决于随之增长的利润方法。 [1] 汤振飞,唐国庆,于尔铿,等.电力市场动态分析[J].中国电机工程学报,2001,21(12):88-92. [2] 白利超,康重庆,夏清.不确定性电价分析[J].中国电机工程学报,2002,22(5):36-41. [3] 白利超,康重庆,夏清.电力市场中发电商的风险决策[J].中国电机工程学报,2004,24(8):1-6. [4] 杨洪明,赖明勇.考虑输电网约束的电力市场有限理性博弈模型的动态演化研究[J].中国电机工程学报,2005,25(23):71-79. [5] Ahmed E.On Puu's Incomplete Information Formulation for the Standard and Multi-team Bertrand Game[J].Chaos,Solitons and Fractals,2006,30(5):1180-1184. [6] 姚洪兴,王梅.动态Bertrand模型的复杂现象与混沌控制[J].陕西师范大学学报(自然科学版),2015,43(2):24-27. [7] Ahmed E,Elsadany A A,Puu T.On Bertrand Duopoly Game with Differentiated Goods[J].Applied Mathematics and Computation,2015,251(C):169-179. [8] Wu F,Ma J H.Hyperchaotic Dynamic of Cournot-bertrand Duopply Game with Multi-Product and Chaos Control[J].Wseas Transactions on Mathematics,2014,13(1):152-160. [责任编辑、校对:周千] Complexity Analysis of Bertrand Model in the Electric Power Market WANGGuo-dong,ZHUOChun-ying (Department of Basic Courses,Chongqing Water Resources and Electric Engineering College,Chongqing 402160,China) To simulate the game playing of different power suppliers in the electric power market,the paper introduces the dynamic Bertrand game model into the electric power market under the constraint conditions of the power transmission grid,establishes the investment model under the bounded rationality,realizes the static-to-dynamic transition process of the investment model through the bounded rationality method and incomplete information method,finds solution to the price equilibrium of the dynamic model,analyzes the stability status of the equilibrium point,and presents the economic explanation. electric power market;Bertrand model;bounded rationality;incomplete information 2016-09-01 王国栋(1981-),男,副教授,主要从事非线性系统复杂性分析研究。 O211;F224.9 ;F270 A 1008-9233(2016)05-0078-04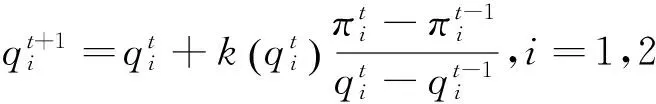



3 结论

