随机脉冲抽象积分方程温和解的存在性

李文胜，周　千,杨　青

(西安航空学院 理学院，陕西 西安 710077)



随机脉冲抽象积分方程温和解的存在性

李文胜，周千,杨青

(西安航空学院 理学院，陕西 西安 710077)

利用凝聚映射不动点定理结合积分预解算子理论，研究了一类随机脉冲一阶抽象积分方程，建立并证明了此类问题温和解的存在性。

积分方程;积分预解算子;随机脉冲

0　引言

近年来，积分微分方程温和解的存在性越来越受关注[1-4],有关随机脉冲的相关知识可参见文献[5-8].

本文主要考虑一类随机脉冲一阶抽象积分方程:

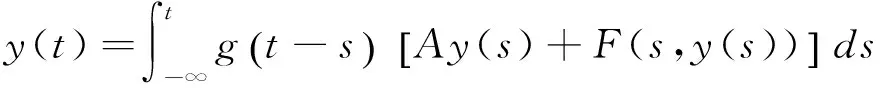
t≠ξk,τ≤t≤T

(1)

(2)

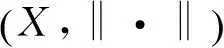
1　预备知识

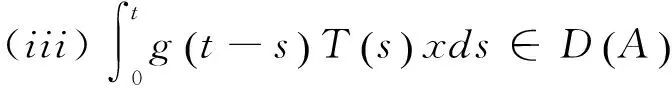
即：

2　主要结果

为了证明系统(1)-(2)温和解的存在性,假设下面条件成立：

并且,对于t∈Rτ,存在一个常数L0>0,使得

H3.存在常数Q>0，使得

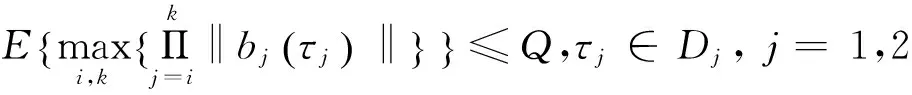
定理2.1 假设条件H1-H3成立,如果

(3)

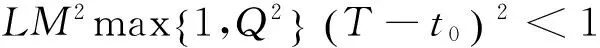
(4)

则系统(1)-(2)的温和解是存在的.

为了应用引理1.2,证明分为以下三步：

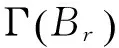
所以

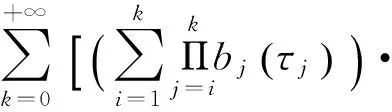
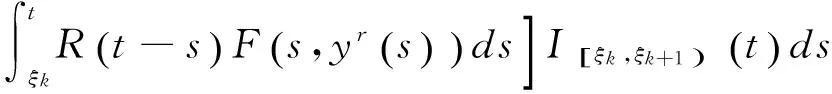
由此,对t∈Rτ,可得

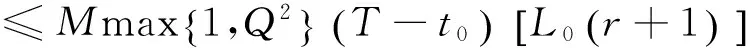
第二步,Γ是压缩的。

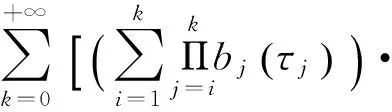
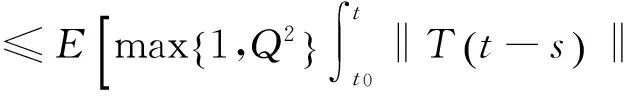
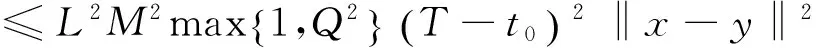
由(4)知,Γ有一个不动点x∈Λ.

第三步，类似于文献[8],Γ是全连续映射。由引理1.2知,随机脉冲积分方程问题(1)-(2)至少有一个温和解.

3　结语

本文研究了一类随机脉冲一阶抽象积分方程，首先将模型转化成定义1.2中的积分形式，然后在给定的条件下，利用积分预解算子理论结合凝聚映射不动点定理，证明了此类积分方程温和解的存在性。

[1] Aníbal C,Manuel P,Daniel S.Weighted Pseudo Almost Periodic Functions,Convolutions And Abstract Integral Equations[J].Journal of Mathematical Analysis and Applications,2016,435(2):1382-1399.

[2] Nugzar S.The Boundary Contact Problem of Electroelasticity And Related Integral Differential Equations[J].Transactions of A.Razmadze Mathematical Institute,2016,170(1):107-113.

[3] Najafalizadeh S,Ezzati R.Numerical Methods for Solving Two-dimensional Nonlinear Integral Equations of Fractional Order by Using Two-dimensional Block Pulse Operational Matrix[J].Applied Mathematics and Computation,2016, 280(C):46-56.

[4] 李文胜.时滞依赖状态的非自治多值偏积分微分方程[J].数学物理学报，2014,34(1),139-149.

[5] Li W S,Chang Y K,Nieto J J.Solvability of Impulsive Neutral Evolution Differential Inclusions with State-dependent Delay[J].Math Comput.Modelling,2009,49(9-10):1920-1927.

[6] Chang Y K,Anguraj A,Mallika M.Existence Results for Non-densely Defined Neutral Impulsive Differential Inclusions with Nonlocal Conditions[J].Journal of Applied Mathematics and Computing,2008,28(1-2):79-91.

[7] 李文胜,周千,韩慧蓉.随机脉冲随机偏发展微分包含解的存在性[J].应用数学学报,2015,38(6)：1059-1073.

[8] Zhao Z H,Chang Y K,Li W S.Asymptotically Almost Periodic,Almost Periodic And Pseudo-almost Periodic Mild Solutions for Neutral Differential Equations[J].Nonlinear Analysis:Real World Applications,2010,11(4):3037-3044.

[9] Yosida K.Functional Analysis[M].6th ed.Berlin:Springer-Verlag,1980.

[10] Lizama C,Poblete V.On Multiplicative Perturbation of Integral Resolvent Families[J].Journal of Mathematical Analysis and Applications.2007,327 (2):1335-1359.

[11] Zhao Z H,Chang Y K,Guérékata G M N.Pseudo-almost Automorphic Mild Solutions to Semilinear Integral Equations in A Banach Space[J].Nonlinear Analysis TMA.2011,74(8):2887-2894.

[12] Sadovskii B N.A Fixed-point Principle[J].Functional Analysis and Its Applications.1967,1(2):74-76.

[责任编辑、校对：周千]

Existence Results of Mild Solution to A Random Impulsive Abstract Integral Equations

LiWen-sheng,ZhouQian,YangQing

(Faculty of Science,Xi'an Aeronautical University,Xi'an 710077)

This paper is concerned with the existence of mild solution to a random impulsive abstract integral equation.Using the condensing mapping fixed point theorem and the integral resolvent operator theory,the existence of mild solutions is established and proven.

Integral Equations;Integral Resolvent Operator;Random Impulsive

2016-07-06

陕西省教育厅科研项目(15JK1379);西安航空学院科研基金(2014KY1210)

李文胜(1984-)，男，陕西礼泉人，讲师，从事泛函微分方程理论研究。

O175.22

A

1008-9233(2016)05-0069-03