基于改进广义正交匹配追踪的OFDM稀疏信道估计

刘远航，黄马驰，赵迎芝

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)



基于改进广义正交匹配追踪的OFDM稀疏信道估计

刘远航，黄马驰，赵迎芝

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

在OFDM稀疏信道中，将压缩感知中的广义正交匹配追踪(GOMP)重构算法用到OFDM信道估计中。由于其信道重构的精度比较低，根据其特点做出了改进，提出了一种用于OFDM稀疏信道估计的改进广义正交匹配追踪算法。该改进算法能够在不需要预知信道稀疏度的情况下准确恢复出信号。根据实验和仿真结果可以看出，该改进算法与LS算法、OMP算法、GOMP算法相比，在同样的环境下误比特率以及均方误差相对比较低，而且运算速度比较快，具有一定的实用性。

压缩感知；正交频分复用；信道估计；广义正交匹配追踪

正交频分复用(OFDM)技术具有良好的抗频率选择性衰落性能和较高的频带利用率，成为高速数据传输的关键技术之一[1]。目前OFDM技术已经广泛应用于无线通信系统。信道估计是通信领域的一个研究热点，它是进行相关检测、解调、均衡的基础[2]。信道估计的质量对整个通信系统的性能起着重要的作用[3]。采用基于导频的信道估计是OFDM系统常用的信道估计方法[4]，其中的信道估计算法如最小二乘法(Least Square，LS)[5]算法结构简单，计算复杂度低，是先通过估计出导频子载波处的信道信息，再通过插值手段重构数据子载波上的信道信息，该方法适应于非稀疏信道的估计，当信道的多径个数比较少时候，该方法的性能并不是很理想。

压缩感知(Compressive Sensing，CS)理论展示了一种全新的信号采集处理方法，对可压缩的稀疏信号以远低于奈奎斯特速率的方式进行采样，仍能够精确地恢复出原始信号[6]。随着压缩感知技术的不断发展与成熟，近年来压缩感知技术被国内外的一些学者应用到通信与信号领域中的OFDM稀疏信道估计中。由于无线信道通常具有稀疏性，即抽头系数接近于零的元素或数值为零的元素相对比较多，因此需要估计的多径参数减小。基于压缩感知的信道估计可以通过一部分导频处的信息估计信道多径参数，再重构出信道的信息，而无需再根据插值法来得到数据子载波上的信道信息，减小了导频的开销，因而能够有效地降低信道估计误差和提高系统频谱利用率，因此，稀疏信道的估计算法一直为学术界和工业界的研究热点[7]。在文献[8]中作者提出了一种将匹配追踪(MP)算法应用于OFDM稀疏信道估计的算法，在文献[9]中作者提出了基于正交匹配追踪(OMP)算法的OFDM稀疏信道估计法。而文献[10]提出了一种广义正交匹配算法(GOMP)，GOMP则是选择与残差乘积最大的少数几个原子，OMP算法是一种特殊的GOMP算法。相比于OMP算法，GOMP具有更高的运算速度。

1　OFDM 系统

在OFDM系统中，当信道的相干时间远大于OFDM符号的周期时，在一个OFDM符号中的信道参数可以认为是不变的，信道的冲激响应可以表示为

(1)

式中：L是OFDM信道的长度；hi是t时刻第i个抽头的复增益，该信道的稀疏性主要表现在[h0,h1,h2,…,hL-1]中数值比较大的几个相对较少的元素或非零元素的个数，而其中临近于零的元素或数值为零的元素相对较多；τi是时刻第i个抽头的延时。

假设OFDM系统中有N个子载波，其中用来传送导频信息的子载波有P个。接收端的信号y维数为N×1，可以表示为

y=XH+W=XFh+W

(2)

式中：N×N维发送信号矩阵X可以表示为X=diag(x(0),x(1),x(2),…,x(N-1))；h=[h0,h1,h2,…,hL-1]，h为信道的离散时域冲激响应；H为对应的频域响应；F为N×L维快速傅里叶变换矩阵；W是N×1维向量的加性高斯白噪声。

设P×N维的选择性矩阵S，N个子载波通过矩阵S选择出其中的P个导频位置，P个导频信号处在接收端收到的对应信号则可以表示为

yp×1=Xp×pFP×LhL×1+WP×1

(3)

在式(3)中，yP×1为观测矢量，AP×1=Xp×pFP×L为测量矩阵。根据式(3)恢复hL×1的过程可以建模为有噪情况下稀疏信号重建问题，因此可以采用压缩感知技术重构出稀疏向量hL×1，然后再通过HP×1=FP×LhL×1求出信道的频域冲击响应采样值即可。

2　一种改进的广义正交匹配追踪算法

广义正交匹配算法(GOMP)是在每一次迭代时选择与残差乘积最大的少数几个原子。相比于OMP算法，GOMP具有运算时间更快与运算复杂度更低的优点。广义正交匹配追踪算法的算法流程如下：

输入：M×N维测量矩阵A，N×1维观测向量y，初始化每次选择原子数S，信道是K稀疏的。

输出：信道稀疏表示的系数估计h^，N×1维残差rt。

1)初始化r0=y，索引值为Λ0=Ø，候选集A0=Ø，阶段t=1。

3)令Λt=Λt-1∪J0，更新索引集At=At-1∪aj(这里包含的所有j∈J0)。

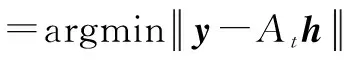
5)t=t+1，如果t≤min(K,M/S)，则返回第2)步，否则停止迭代。

从以上步骤看出广义正交匹配算法(GOMP)是在每一次迭代时选择与残差乘积最大的少数几个原子，在每次迭代过程中可能会选择出错误原子。其次GOMP算法在信道的稀疏度预先知道的情况下才能够准确重构出信号，但是在实际环境中，信道的稀疏度往往是无法预先知道的。用GOMP算法进行信道估计，经过实验和仿真得到的误码率跟均方误差在效果上不如OMP算法。因此针对此特点，在GOMP算法的基础上进行改进，提出了一种改进广义正交匹配追踪(GGOMP)算法，在未预知稀疏度的条件下能够准确估计出信道的信息而且误码率比较低。

在文献[11]中作者提出了一种自适应压缩感知重构算法，提高了稀疏度估计的准确性。在文献[12]中作者提出了一种门限自适应的压缩感知重构算法，提高了信号重构的精确度。在此基础上，改进的广义正交匹配追踪算法步骤如下：

输入：M×N维的测量矩阵A，N×1维观测向量y，初始化选择的原子个数S。

输出：信道稀疏表示的系数估计h^，N×1维残差r。

1)初始化残差r0=y，索引值为Λ0=Ø，候选集A0=Ø，初始化支撑集L=S，阶段值t=1;

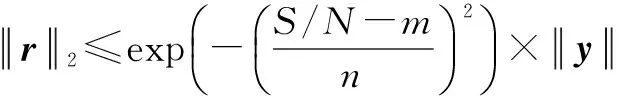
3)计算u=abs[ATrt-1]也就是计算⟨rt-1,aj⟩,1≤j≤N，选择出u中最大的L个值，将这些值对应的A的列序号构成集合J0；

4)令Λ=Λt-1∪J0，AΛ={aj}，其中所有的j∈Λ；

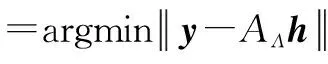
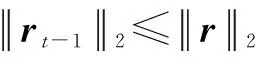
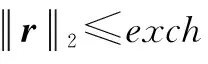
8)令t=t+1，L=t*S，继续执行步骤2)；

9)更新索引集和残差，Λt=Λ，rt=r，t=t+1。继续执行步骤2)。

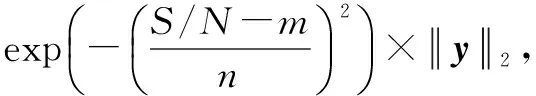
3　仿真与性能分析

为了验证提出算法的有效性，本文进行了如下的仿真，系统参数为:信道带宽24 kHz，OFDM子载波数N=512，采样点数为512，调制方式为QPSK调制，循环前缀长度CP=N/4=128，导频数目为32，其中非零抽头数目为6，其下标为 1，10，15，23，34，42。系统仿真采用误码率 (BER)和归一化均方误差(MSE)作为指标， 来将LS算法和基于压缩感知的OMP算法、GOMP算法以及改进的GGOMP算法在信道估计性能方面的差异进行对比。归一化均方误差公式为

(4)

式中：m是仿真次数；hi^表示第i次仿真实验的信道冲激响应估计值；hi表示第i次仿真实验的信道冲激响应真实值。

3.1不同算法的 MSE 和 BER 性能对比

OMP算法、GOMP算法以及改进的算法GGOMP的3种信道重构算法和LS算法均采用32个导频，为了更能突出对比，LS算法采用能够使其性能达到最佳的均匀导频，而基于压缩感知的重构算法采用随机导频。GOMP与GGOMP的初始化原子个数S均为2，仿真实验如图1和图2所示，是几个不同算法的均方误差和误码率对比曲线图。从实验结果看出，基于压缩感知的OMP算法与GOMP算法、GGOMP算法随着信噪比的增加均方误差与误码率均逐渐减小。GGOMP算法的精确重构能力以及BER性能是表现最好的，优于OMP算法、GOMP算法及LS算法。OMP算法其次，而LS算法不能精确进行信道估计。

图1　不同算法均方误差对比曲线

图2　不同算法误比特率对比曲线

3.2初始化步长对MSE性能的影响

在进行仿真的过程中，需要研究GGOMP算法初始的步长大小，是否会影响信道估计的性能和运行时间。如图3所示，比较了GGOMP的初始步长对误码率性能影响。当步长S取不同值的时候，对信道估计的性能有影响。随着S的逐渐增加，归一化均方误差(MSE)逐渐减小。

图3　GGOMP的初始步长对均方误差的影响

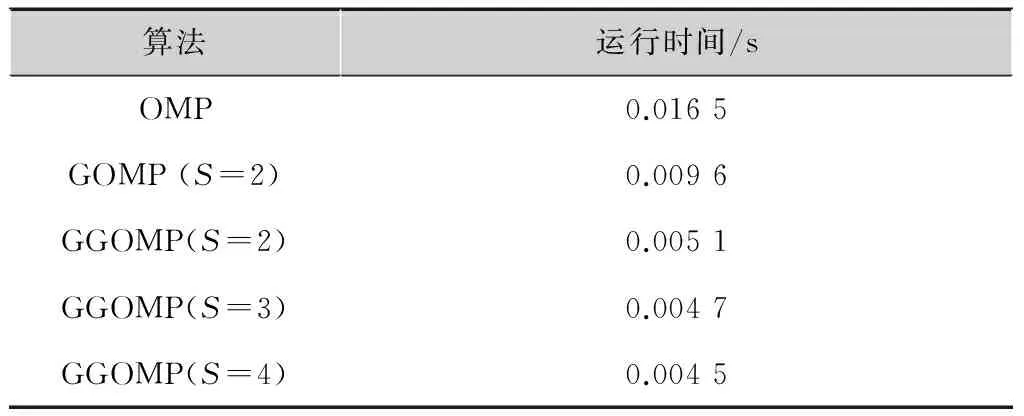
3.3各种重构算法运行时间的比较

下面对OMP算法、GOMP算法和GGOMP算法的运算时间做比较。仿真计算机的配置为Intel双核主频2.7 GHz的处理器，操作系统为微软Windows7，内存为2 Gbyte，用MATLABR2012a软件进行仿真。表1给出几种压缩感知重构算法的平均运行时间。通过比较，可以观察出GGOMP算法比OMP算法和GOMP算法的运算时间更短。由理论分析可知，GOMP是选择与残差内积最大的几个原子，而OMP每次只选择与残差内积最大的一个原子。相比于OMP算法，GOMP具有更高的运算速度。GGOMP算法在本次迭代残差大于上次迭代残差时，支撑集会逐渐增大，由于每次迭代选择的原子数增加， 使得算法运行时间相比于GOMP逐渐减少。在GGOMP算法中，当初始步长增加时，每次选择的原子个数增加了，因此运行时间减小了。

表1各种算法运行时间比较

算法运行时间/sOMP0.0165GOMP(S=2)0.0096GGOMP(S=2)0.0051GGOMP(S=3)0.0047GGOMP(S=4)0.0045

4　小结

本文针对GOMP算法在OFDM信道估计中存在的缺点提出改进广义正交匹配追踪(GGOMP)算法。在导频数和信噪比相同时，采用改进广义正交匹配追踪算法的信道估计方法的误码率和均信道重构性能都很好，而且能够在不需要预知稀疏度的情况下重构出信号，运行的时间比较短，具有实用性。

[1]丁敬校，王可人，陈小波.基于正交匹配追踪的 OFDM系统稀疏信道估计算法[J].通信对抗，2012，31(1)：6-11.

[2]张继东，郑宝玉.基于导频的OFDM信道估计及其研究进展[J].通信学报，2003，24(11)：116-123.

[3]彭钰，侯晓赟，魏浩.压缩感知时频双选信道估计[J].信号处理，2014，30(1)：119-126.

[4]LANG T，SADLER B M，DONG M. Pilot-assisted wireless transmissions: general model，design criteria， and signal processing[J]. IEEE signal processing magazine，2004，21(6)：12-25.

[5]LIN J C.Least-squares channel estimation assisted by self-interference cancellation for mobile pseudo-random-postfix orthogonal-frequency division multiplexing applications[J]. IET communications，2009，3(12)：1907-1918.

[6]DAVENPORT M A，BOUFOUNOS P T，WAKIN M B，et al. Signal processing with compressive measurements[J].IEEE journal of selected topics in signal processing，2010，4(2)：445-460.[7]陈宇，未元，梁彦，等.IQ不平衡OFDM系统高性能稀疏信道估计算法[J].数据采集与处理，2014，29(6)：986-991.

[8]朱行涛，刘郁林，徐舜.一种基于匹配追踪的OFDM稀疏信道估计算法[J].微波学报，2008，24(2)：73-76.

[9]何雪云，宋荣方，周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究[J].南京邮电大学学报，2010，30(2)：60-65.

[10]WANG J，KWON S，SHIM B. Generalized orthogonal matching pursuit[J].IEEE transactions on signal processing，2012(60)：6202-6216.

[11]甘伟，许录平，罗楠，等.一种自适应压缩感知重构算法[J].系统工程及电子技术，2011，33(9)：1948-1953．

[12]王韦刚，杨震，胡海峰.分布式压缩感知实现联合信道估计的方法[J].信号处理，2012，28(6)：778-784．

刘远航(1990— )，硕士生，主研无线通信中的信道估计；

黄马驰(1990— )，硕士生，主研移动通信与SDN；

赵迎芝(1990— )，女，硕士生，主研无线通信。

责任编辑：许盈

Sparse channel estimation for OFDM systems based on modified generalized orthogonal matching pursuit algorithm

LIU Yuanhang，HUANG Machi，ZHAO Yingzhi

(ChongqingKeyLabofMobileCommunicationsTechnology，ChongqingUniversityofPostandCommunications，Chongqing400065，China)

In OFDM sparse channel, the generalized orthogonal matching pursuit reconstruction algorithm in the compressive sensing technology is applied to OFDM channel estimation. Because it has a very low signal reconstruction accuracy , the algorithm based on the modified generalized orthogonal matching pursuit algorithm is presented in the light of the characteristics of it. The improved algorithm is proposed for OFDM channel estimation which can recover the signal without the knowledge of the sparsity of channel. According to the experimental and simulation results, compared with the LS algorithm and the OMP algorithm, the GOMP algorithm, the proposed algorithm not only gets much lower mean square error and bit error rate under the same condition, but also has fast calculation speed, it is much suitable for real application.

compressive sensing; OFDM; channel estimation; GOMP

TN929.5

ADOI：10.16280/j.videoe.2016.10.025

长江学者和创新团队发展计划项目(IRT1299)；重庆市科委项目(CSTC2013YYKFA40010)；重庆市科委重点实验室专项

2016-02-21

文献引用格式：刘远航，黄马驰，赵迎芝.基于改进广义正交匹配追踪的OFDM稀疏信道估计[J].电视技术，2016，40(10)：127-130.

LIU Y H，HUANG M C，ZHAO Y Z. Sparse channel estimation for OFDM systems based on modified generalized orthogonal matching pursuit algorithm [J].Video engineering，2016，40(10)：127-130.