加权稀疏的混合噪声去除模型

朱平芳，陈利霞，1b，2

(1.桂林电子科技大学 a.数学与计算科学学院 广西高校数据分析与计算重点实验室；b.广西高校图像图形智能处理重点实验室，广西 桂林 541004；2. 广西信息科学实验中心，广西 桂林 541004)



加权稀疏的混合噪声去除模型

朱平芳1a，陈利霞1a，1b，2

(1.桂林电子科技大学 a.数学与计算科学学院 广西高校数据分析与计算重点实验室；b.广西高校图像图形智能处理重点实验室，广西 桂林 541004；2. 广西信息科学实验中心，广西 桂林 541004)

针对混合噪声，结合加权稀疏与变分，提出了新颖的去噪模型。首先，进行PCA训练自适应字典，再结合非局部相似性，利用噪声的特性进行加权编码。最后，结合变分正则项，再利用对偶方法求出恢复后的图像。仿真实验表明，该算法不仅提高了图像的峰值信噪比，而且更好地保留图像的重要特征，提高图像的视觉效果。

混合噪声；加权编码；非局部相似；变分； 对偶方法

1　图像混合噪声

图像在获取和运输的过程中不可避免的会受到噪声的污染，而被噪声污染的图像会影响图像的后续处理，例如边缘检测、目标识别和图像分割等。因此去噪是图像数字图像处理的一个重要问题，其主要目是在保存图像的细节、纹理和边缘等特征下，从给定的噪声图像中恢复理想的图像。

由于噪声的多样性，存在多种混合噪声，本文主要研究加性高斯白噪声 (AWGN) 和脉冲噪声(IN)的混合。

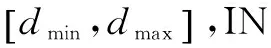
(1)

由于混合噪声分布复杂，有效的去除是一个相当困难的问题。近年来， Abreu等[1]提出了基于中值信号相互联系的滤波器，该算法能够很好地去除脉冲噪声，但是去除混合噪声时，图像边缘与细节等信息也受到较大的影响。Cai等[2]提出的去除混合噪声的算法计算复杂。Xiao等[3]先利用中值类滤波进行脉冲噪声检测，最后用l1-l0最小优化问题求解去噪图像。文献[3]改善了去噪图像的视觉质量，但是计算量大。2013年，文献[4]提出了基于加权学习字典去除混合噪声。Jiang等[5]在文献[4]的基础上结合非局部稀疏表示的方法(JZY模型)，同时去除AWGN和IN，并且不需要先进行脉冲噪声的检测。Zhang等[6]提出基于分组稀疏表示的方法(ZZG模型)去除混合噪声，该算法得到的去噪图过于光滑，其他混合噪声去除算法[7-9]。

虽然上述去噪算法是针对混合噪声提出的，并且在某种程度上起到抑制混合噪声效果，但图像的边缘与细节等重要信息也受到很大影响。针对这一问题，本文提出了一种新型的混合噪声去除算法。该算法将稀疏加权编码与变分相结合，能更好地保存图像的重要信息。仿真实验表明，新算法对图像重要特征的保留有一定的改善作用。

2　相关工作

一般情况下，去除混合噪声分两步：首先去除IN[10]，再去除AWGN，但是在实际的去噪中，很难将IN和AWGN分离。[5]提出了基于非局部稀疏加权编码模型(JZY模型)，同时去除AWGN和IN

(2)

式中：W稀疏加权权重；Φ为稀疏字典；α为稀疏编码；R(α)为正则项；λ为已知的正则项参数。考虑到非局部与局部之间的联系，引入非局部项，式(2)可以写成

(3)

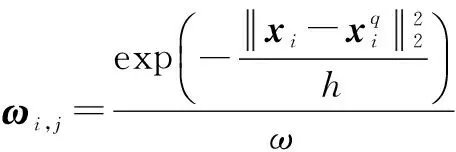
(4)

式中：Γ为伽马函数；σγ为标量参数，由β决定f(γ)的分布类型。特别地，当β=1时，f(γ)服从拉普拉斯分布；当β=2时，f(γ)服从高斯分布。文献[5]指出，当f(γ)服从拉普拉斯分布时，图像去噪的直方图越接近原图像，所以用l1范数约束非局部项，即JZY模型

(5)

3　新模型设计

为了更好地保留图像的重要特征，增强图像的混合去噪能力，本文在JZY模型的基础上引入变分，得到新模型

(6)

式中：第一项为忠诚项；第二项是非局部项；第三项为变分项；λ,λ1为非负正则化参数，为了保留图像的边缘信息，模型(6)分2个子问题来求解。

子问题1：更新编码。其模型为

(7)

式中：λ平衡稀疏项和非局部正则项；W是对角权重矩阵。

(8)

式中：a是常数用来控制Wii的下降速度。接下来通过迭代权重的方法去求解稀疏编码，Daubechies 等[11]假设V为对角矩阵，最初值为单位矩阵，通过(k+1)th迭代，对角矩阵V的每个元素为

α(k+1)=(ΦTWΦ+V(k+1))-1(ΦTWy-ΦTWΦμ)+μ

(9)

迭代V和稀疏编码α之后，可以得到较为理想的稀疏编码，权重迭代的收敛性已经证明文献[11]，其中求解以及更新非局部项μ的具体方法和步骤依据文献[5]。

子问题2：恢复图像。其模型为

(10)

式(10)的对偶问题为

(11)

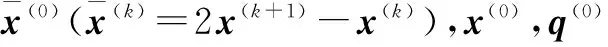
(12)

然后用牛顿方法得到去噪图像，即

(13)

1)输入：字典Φ，噪声图像y，参数λ,λ1，迭代次数K。

2)最初化：最初化W通过式(8)，最初化μ=0，把图像聚类以后，在每一类中用PCA方法训练子字典作为初始字典，迭代次数k=1,2,…,K。

3)更新稀疏编码α：α(k)=(ΦTWΦ+V(k))-1(ΦTWy-ΦTWΦμ)+μ。

4)更新x(k)=Φα(k)和非局部项μ。

5)更新残差e(k)=y-x(k)，具体的更新方法见文献[5]。

6)更新权重W通过残差e(k)和式(8)。

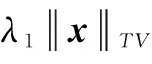
8)输出：去噪图像x。

4　实验仿真及结果分析

为了更好地评价新算法的性能，将本文提出的算法与文献[6]的ZZG算法和文献[5]的JZY算法进行比较。测试图为大小全部为512×512的Pirate、Peppers和Jetplane，如图1所示。对于混合噪声，AWGN的标准差分别为σ=10,20,30，IN的强度分别为p=30%,40%,50%，不同程度的噪声图如图2所示。对于非局部参数λ，当噪声强度为σ=10,λ=0.5的时候，迭代8次，当噪声强度为σ=20,30,λ=1，分别迭代10和12次，参数λ1=0.01，字典分块大小为7×7，其余的参数选取与文献[5]相同。本实验是在处理器为Inter Core i3、内存为2.3-Ghz dual-core 的PC机上运行，Matlab 版本为R2010b。

图1　测试图

图2　噪声图像

本文利用峰值信噪比 (PSNR) 及图像特征相似度 (FSIM)[5]来评估去噪的图像质量。

实验一：以“Pirate”为比较对象，其中噪声强度为σ=30,p=40%。从图3可以清楚的看出，图3b还存在很多噪声，图像的边缘和脸部(嘴巴、鼻子、眼睛和下巴)比较模糊，特别是手链、手指以及手指上的戒指；图3c虽然在边缘处理的比图3b图好，但是相比图3d和图3c的边缘处理相对比较模糊，从脸部轮廓和脸部(嘴巴、鼻子、眼睛和下巴)可以明显地看出图3d优于图3b与图3c，进一步从手腕的链子和手指的戒指可以看出本文算法能够很好保存图像边缘特征。

实验二：以Peppersσ=20,p=50%为研究目标。从图4可知，图4b辣椒的边缘和辣椒梗上面出现不属于辣椒本身的东西；从竖着的辣椒和最小的辣椒梗可以很明显地看出图4d优于图4b和图4c。

图3　Pirate去噪比较 (σ=30,p=40%)

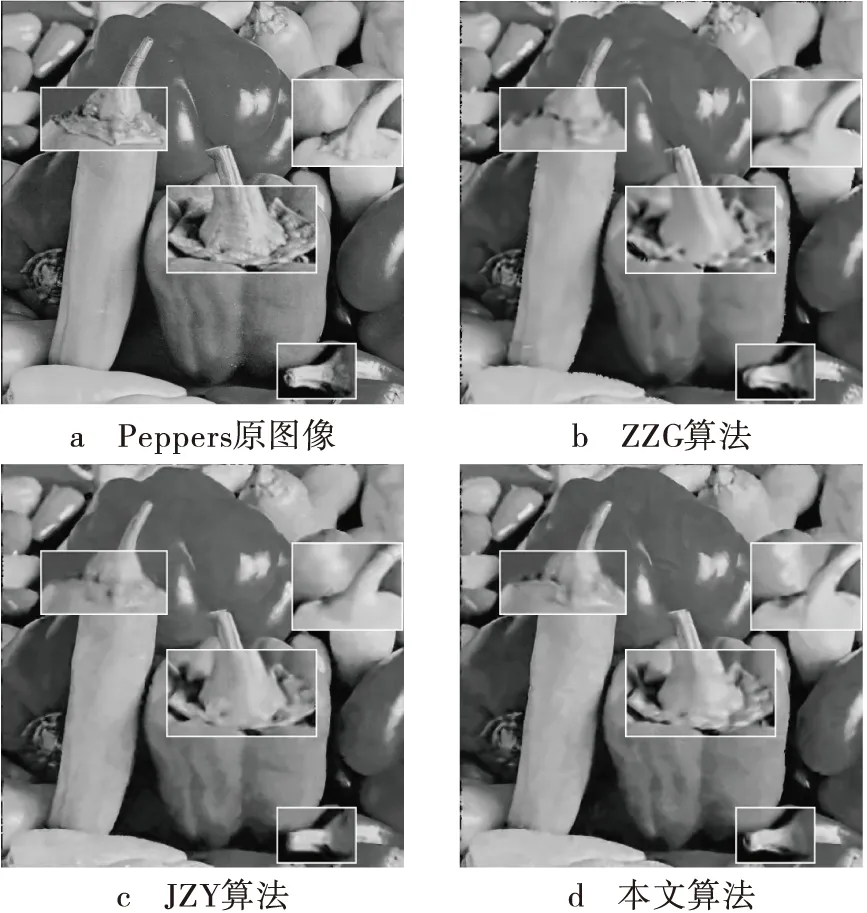
图4　Peppers去噪比较 (σ=20,p=50%)

由此可见，在图视觉质量上，提出算法的去噪图要接近于原图像，使得去噪图像看起来更自然，特别是在图像的细节和边缘化上。

进一步从表1可知，本文算法在不同强度噪声下的去噪图的PSNR和FSIM也都要高于对比算法。

综上所述，本文算法无论在主观上(图像质量)还是客观上(PSNR 和FSIM)都要优于对比算法。

5　结论

本文提出了一种新型的去除混合噪声模型，该算法将稀疏加权编码与变分相结合，有效保存了图像的边缘信息，训练稀疏字典和编码以后，最后用对偶方法得到去噪图像。仿真实验显示，无论从主观标准还是客观标准，本文算法对不同程度的混合噪声都具有很好的抑制能力。

表1不同混合噪声去除算法的PSNR和FSIM

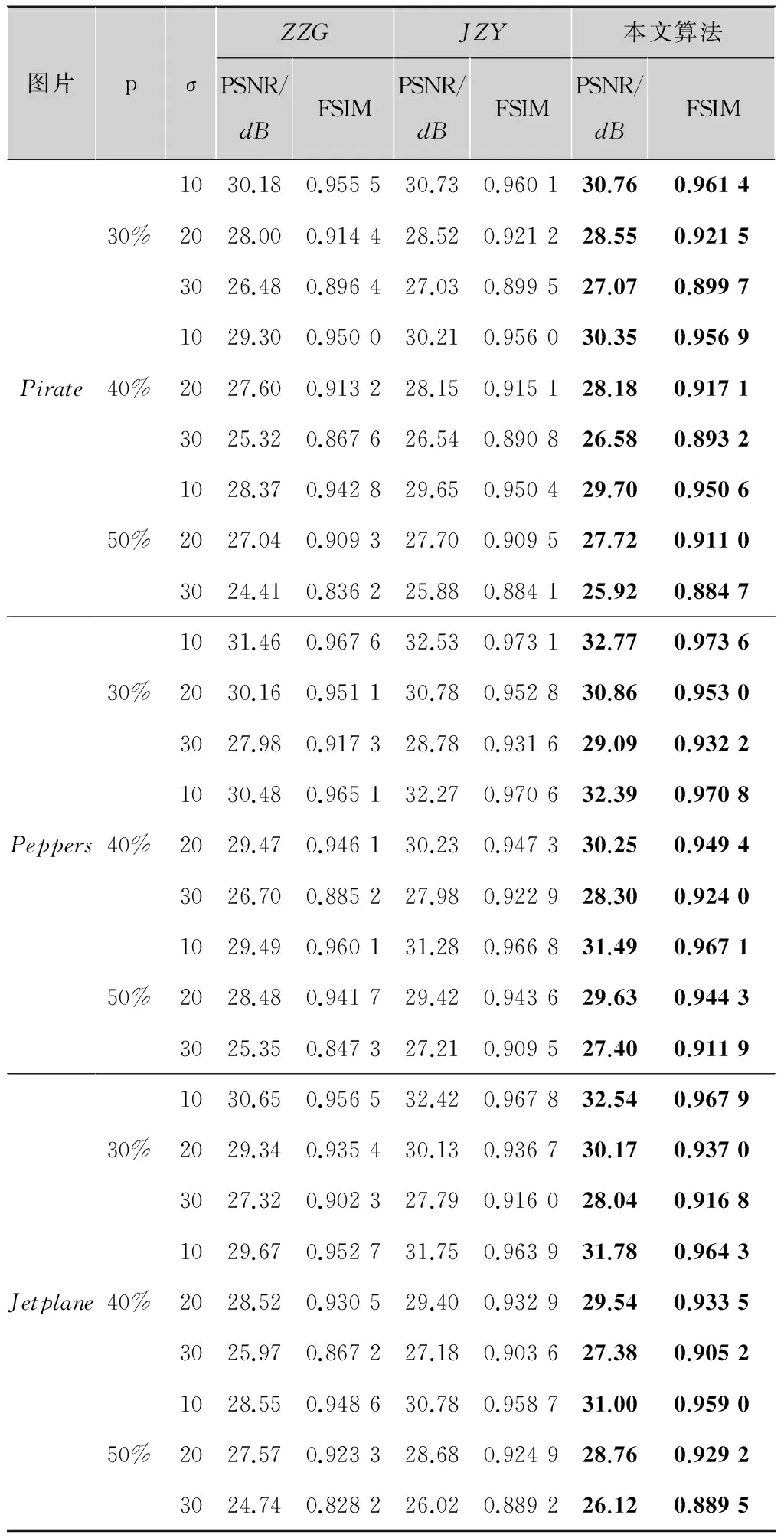
图片pσZZGJZY本文算法PSNR/dBFSIMPSNR/dBFSIMPSNR/dBFSIMPirate30%1030.180.955530.730.960130.760.96142028.000.914428.520.921228.550.92153026.480.896427.030.899527.070.899740%1029.300.950030.210.956030.350.95692027.600.913228.150.915128.180.91713025.320.867626.540.890826.580.893250%1028.370.942829.650.950429.700.95062027.040.909327.700.909527.720.91103024.410.836225.880.884125.920.8847Peppers30%1031.460.967632.530.973132.770.97362030.160.951130.780.952830.860.95303027.980.917328.780.931629.090.932240%1030.480.965132.270.970632.390.97082029.470.946130.230.947330.250.94943026.700.885227.980.922928.300.924050%1029.490.960131.280.966831.490.96712028.480.941729.420.943629.630.94433025.350.847327.210.909527.400.9119Jetplane30%1030.650.956532.420.967832.540.96792029.340.935430.130.936730.170.93703027.320.902327.790.916028.040.916840%1029.670.952731.750.963931.780.96432028.520.930529.400.932929.540.93353025.970.867227.180.903627.380.905250%1028.550.948630.780.958731.000.95902027.570.923328.680.924928.760.92923024.740.828226.020.889226.120.8895

注：最好的PSNR和FSIM标注为粗体。

[1]ABREUE，LIGHTSTONEM，MITRASK，etal.Anewefficientapproachfortheremovalofimpulsenoisefromhighlycorruptedimages[J].IEEEtransactionsonimageprocessing，1996，5(6)：1021-1025.

[2]CAIJF，CHANR，NIKOLOVAM，etal.Fasttwo-phaseimagedeblurringunderimpulse[J].Journalofmathematicalimageandvision，2010，36(1)：46-53.[3]XIAO Y，ZENG T Y，YU J，et al. Restoration of images corrupted by mixed Guassian-impulse noise via l1-l0minimization[J]. Pattern recognition，2010，44(8)：1708-1720.

[4]LIU J，TAI X C，HUANG H Y，et al. A weighted dictionary learning models for denoising images corrupted by mixed noise[J]. IEEE transactions on image processing，2013，22(3)：1108-1120.

[5]JIANG J，ZHANG L，YANG J，et al. Mixed noise removal by weighted encoding with sparse nonlocal regularization[J]. IEEE transactions on image processing，2014，23(6)：2651-2262.

[6]ZHANG J，ZHAO D B，GAO W，et al. Group-based sparse representation for image restoration[J]. IEEE transactions on image processing，2014，23(8)：3336-3351.

[7]BARCELOS C，BARCELOS E. A well-balanced and adaptive variational model for removal of mixed noise[J]. Computers and electrical engineering，2014，40(7)：2027-2037.

[8]LIU G，HUANG T Z. A new two-stage method for image restoration under mixed gaussian impulse noise[C]//International Conference on Computer Science and Artificial Intelligence (ICCSAI).[S.l.]：IEEE，2015：181-185.

[9]JIANG J L，YANG J，CUI Y，et al. Sparse nonlocal priors based two-phase approach for mixed noise removal[J]. Singal processing，2015(16)：101-111.

[10]周军妮，王燕妮，杨润玲，等.基于噪声检测的高密椒盐噪声自适应滤波算法[J].电视技术，2014，38(19)：41-46.

[11]DAUBECHIES I，DEVORE R，FORNASIER M，et al. Iteratively re-weighted least squares minimization for sparse recovery[J]. Communications on pure and applied mathematics，2010，63(1)：1-38.

[12]CHAMBOLLE J，POCK T. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of mathematical imaging and vision，2011，40(1)：120-145.

朱平芳(1990— )，女，硕士生，主研数字图像处理；

陈利霞(1979— )，女，研究生导师，主要研究方向为偏微分方程理论、小波理论及其在图像处理中的应用。

责任编辑：时雯

Mixed noise removal model by weighted sparse representation

ZHU Pingfang1a，CHEN Lixia1a，1b，2

(1a.SchoolofMathematicsandComputingScience；1b.GuangxiCollegesandUniveritiesKeyLaboratoryofIntelligentProcessingofComputerImagsandGraphicsandGraphics，GuilinUniversityofElectronicTechnology，GuangxiGuilin541004，China；2.GuangxiExperimentCenterofInformationScience，GuangxiGuilin541004，China)

Aiming at the mixed noise， a novel denoising model based on weighted sparse and variational is proposed in this paper. First， PCA method is used to train adaptive dictionary， and then， combined the non-local similarity with the characteristics of noise， it can get the weighted coding. Finally， the restored image is obtained by using the dual method. Experimental results showed that this algorithm can not only improve image’s peak signal to noise ratio (PSNR)， but also preserve the important features， which result in improving the visual quality of the image.

mixed noise； weighted coding； non-local similarity； variational； dual method

TN911.72

ADOI：10.16280/j.videoe.2016.10.007

国家自然科学基金项目(61362021)；广西自然科学基金项目(2013GXNSFDA019030；2012GXNSFBA053014；2014GXNSFDA118036)；广西高校图像图形智能处理重点实验室项目(GIIP201408；GIIP201503)

2016-03-30

文献引用格式：朱平芳，陈利霞.加权稀疏的混合噪声去除模型[J].电视技术，2016，40(10)：33-36.

ZHU P F，CHEN L X.Mixed noise removal model by weighted sparse representation [J].Video engineering，2016,40(10)：33-36.