基于快速不动点连续的压缩感知重构算法

郭青青，李　雷

(南京邮电大学　视觉认知计算与应用中心，江苏 南京 210046)



基于快速不动点连续的压缩感知重构算法

郭青青，李雷

(南京邮电大学视觉认知计算与应用中心，江苏 南京 210046)

不动点连续(FPC)算法是一种凸优化算法，针对该算法收敛速度较慢的现象，提出了一种快速的不动点连续(FFPC)算法，算法引入线性搜索步长，选择合理的步长参数，利用前两次迭代结果的特殊线性组合值作为下次迭代的初始值，提高每次迭代的精度，从而加快收敛速度。FFPC算法的收敛性在实验中得到了验证，同时，仿真实验表明，FFPC算法的收敛速度有所提高，重构质量也比其他算法更好。

凸优化算法；压缩感知；快速不动点连续

在信号采样和处理的过程中，压缩感知(Compressed Sensing，CS)[1]被视为是一种很具发展前景的理论框架， 它打破了传统香农采样定理的限制，成为一种新型的信号采样和处理的理论，主要涉及3个问题：信号的稀疏表示、观测矩阵的设计和信号重构算法的设计[2]。CS理论指出，具有稀疏性或可压缩性的信号可通过求解不适定的数学反问题，由少量的观测值完成对原始信号的精确重构。

压缩感知的重构算法主要分为3类[3]：1)贪婪算法，例如匹配追踪(Matching Pursuit，MP)系列；2)凸优化算法，例如内点法(Interior-Point Algorithm，IPA)，梯度投影算法(Gradient Projection Algorithm，GA)，迭代收缩阈值算法(Iterative Shrinkage-Thresholding Algorithm，IST)[4]和不动点方法(Fixed-Point Continuation Method，FPC)[5]；3)组合算法。这些算法各有利弊，其中，对凸优化算法的研究比较完善，其相关定理也有明确的界定。

目前，凸优化算法中应用最为广泛的是IST方法及其改进方法，例如：两步迭代收缩阈值(Two-step IST，TwIST)[6]快速迭代阈值(Fast IST，FIST)方法[7]。另一方面，不动点连续性(Fixed Point Continuation，FPC)方法作为一种新型方法被提出[8]，该方法从算子分裂技术的角度可以看作是IST的改进模型，其利用不动点定理实现迭代，应用的范围更为宽泛，并且，其不需要计算二阶Hessian阵，大大降低了计算复杂度，同时，对FPC方法的研究具有一定的意义和价值。本文将提出一种快速的FPC算法，在不失原算法重构性能的前提下，实现更快速和高效的重构效果。

1　压缩感知

1.1压缩感知的重构模型

根据CS理论，假设是x∈Rn是K阶稀疏信号，A∈Rm×n是感知矩阵，则通过求解下面l0最小化问题，可从少量不完整的观测值b=Ax中恢复出原始信号

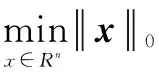
(1)

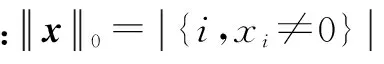
(2)

(3)

式中：μ>0，是惩罚项系数。当μ趋于0时，式(3)的解便趋于式(2)的解[10]。

1.2不动点迭代连续(Fixed Point Continuation Algorithm，FPC)算法

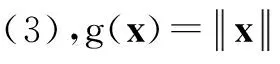
0∈T(x)0∈(x+τT1(x))-(x-τT2(x))

(I+τT1)x∈(I-τT2)x

x=(I+τT1)-1(I-τT2)x

(4)

因此，F(x)的最小解迭代公式为

xn+1=(I+τT1)-1(I-τT2)xn

(5)

命题1：对于特定的τ>0，假设X*是式(3)的最优解集，则x*∈X*当且仅当

(6)

于是，不动点迭代公式可表示为

(7)

sv(·)=sgn(·)max{|·|-v,0}

(8)

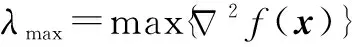
另一方面，考虑连续性，文献[11]中设计了一组递增的序列{μi}，依次取μi+1进行每轮迭代，本文的改进算法均是基于此不动点连续(Fixed-Point Continuation，FPC)算法进行的。

2　快速不动点连续算法(Fast FPC，FFPC)

2.1快速不动点连续算法

FPC算法的主迭代主要包含两步：梯度下降步和阈值收缩步。算法迭代步骤简单，但收敛速度较慢，有待进一步提升。本文根据快速迭代收缩阈值(FIST)算法的改进思想，引入合理的参数t，计算出下降步长的搜索系数，然后利用前两次迭代结果的特殊线性组合计算下次迭代值，从而提高迭代收敛速度，减少迭代的次数。

FFPC算法通过选取合理的序列{tn}来计算迭代系数αn，从而更新每次迭代的公式

yn=xn+αn(xn-xn-1)

(9)

对于FIST算法，序列{tn}的选择有两类形式[12]：

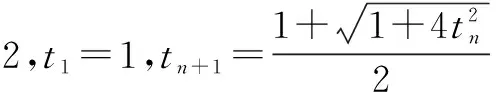
在一定的条件下，两种选择方式的收敛性均已从理论和实验两方面得到了证明。鉴于IST和FPC算法一样的理论框架和迭代原理，选择这两种序列均具有一定的可行性，但序列1更不失一般性，因此，本文将采用序列1的系数形式。另外，后文将设计相应的仿真实验来验证算法的收敛性和可行性。

通过FFPC算法求解问题(3)的迭代公式如下

(10)

yn=xn+αn(xn-xn-1)

(11)

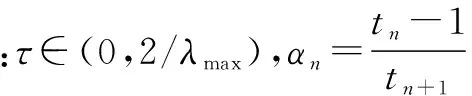
在不动点算法中，参数τ的取值对迭代收敛速率有着重要的作用，其值越大收敛越快，故本文算法将通过Barzilai-Borwein(BB)步来计算参数τ的值，同时，为收敛平稳，在BB方法下选用非单调线性搜索(Nonmonotone Line Search，NMLS)来更新下降步长[11]。于是，快速不动点连续算法步骤如下。

算法1：快速不动点连续(FFPC)算法

2)初始化：感知矩阵A，观测值x0，噪声sig，μ0，τ0，t0和α0。

3)执行：μ=μi+1，重复如下步骤直至收敛。

(1)检查零解。

(2)主迭代：执行k=k+1，重复如下步骤直至满足收敛条件或k≥Imax。

①计算v=τ/μ,yk=xk-1-τ·xk-1。

③更新tk，计算α0。

④计算系数τ。

4)输出：重构信号x*，算法时长time，信噪比SNR。

2.2不动点连续算法的性质

定义1：设X是式(3)问题的一个最优解集，且X≠φ，定义集合Ω，使集合中元素满足下列条件

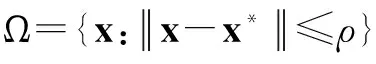
(12)

式中：x*∈X,ρ>0。

引理1：收缩算子sv(·)是非扩张的，即∀x1,x2∈Rn，有以下不等式成立

(13)

引理2：算子hτ(·)是非扩张的，即∀x,x′∈Ω，有以下不等式成立

(14)

当且仅当g(x)=g(x′)时，等号成立。另外，引理1和2的证明过程见文献[11]。

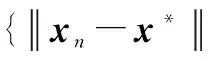
(15)

证明

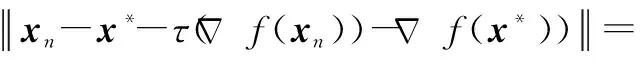
(16)

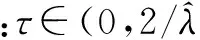
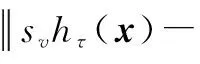
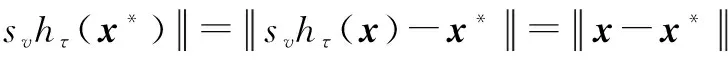
定理2：对于式(3)问题，假设x0∈Ω是不动点迭代的初始点，序列{xn}是迭代值，那么该序列最终会收敛于x*，且x*∈X*∩Ω。

证明：

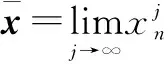
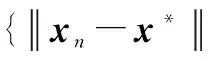
(17)

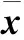
最终，定理证毕[11]。

3　仿真实验

本节实验均是在2 Gbyte内存2.53主频的便携式计算机上进行，软件版本是MATLAB 7.0。

3.1收敛性实验

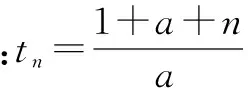
实验将不同参数下，分别计算出迭代步数和每步重构值与原始信号之间的相对误差rerr，相对误差公式如下

(18)

式中：x是每次迭代的重构值；xs是原始值。则从开始迭代到算法终止，相对误差值的变化曲线如图1所示。

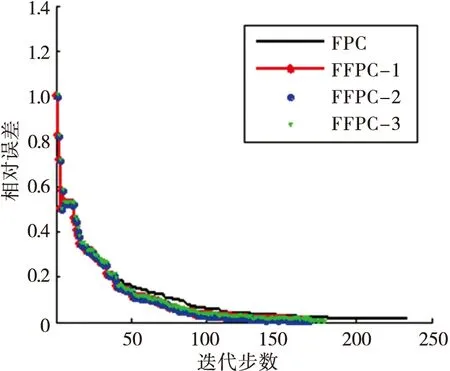
图1　重构值与原始信号间相对误差随迭代步数增加时的变化曲线

从图1可以看出，FFPC算法和原FPC算法的相对误差值均随迭代步数的不断增加而逐渐减小，并且逐步趋近于零，这表明FFPC算法与原算法一样是收敛的，并且，也说明FFPC算法具有可行性和一定的稳定性。另一方面，在相同的实验条件下，FFPC算法相比原算法所需的迭代步数更少，这间接说明FFPC的收敛速度更快。因此，数值实验验证了FFPC算法的收敛性，同时收敛性能也有所提升。

3.2视频帧重构实验

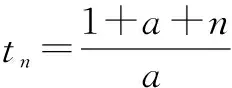
各算法是按列对视频信号进行重构的，故每次实验需要N轮迭代过程。分别利用各算法进行15次重构实验，统计所用实验收敛时的迭代步数，然后计算出每轮迭代步数的平均值，即表1所列数据。表1中数据显示，在不同测量率下，FFPC算法的平均迭代步数均比其他少，这些数值说明FFPC算法的收敛速度有所提高，尤其是当采样率较低的情况下，提高较为明显。

表1不同算法在不同测量率下每轮迭代步数的平均值

deltaITSFPCFFPC-2FFPC-30.3568540390.5394431320.728372120

另外，实验中对各算法的重构时间和峰值信噪比(PSNR)进行了计算和统计，具体数据见表2。这两项指标反映了各算法重构速率和质量的性能。数据表明FFPC算法的重构速率比其他算法都快，尤其与原FPC算法相比。另一方面，FFPC算法在重构质量上相比原FPC有所提升，且较ITS算法也有一定的优势。因此，FFPC算法不仅加快了重构速率，而且提高了重构质量，比其他算法更高效地实现了重构。为更直观地观察各算法的重构效果，本节给出各算法在测量率delta=0.5时的重构对比图像，如图2所示。

表2不同测量率下算法重构的所耗时长和PSNR值

算法delta=0.3delta=0.5delta=0.7时长/sPSNR/dB时长/sPSNR/dB时长/sPSNR/dBITS6.810323.98745.082129.02434.280130.0007FPC10.717322.79945.985628.01034.789229.9778FFPC-25.396024.93354.511630.66354.031631.4201FFPC-35.130824.11354.427230.57674.067231.0078

图2　测量率delta=0.5时的视频帧重构效果对比图

4　小结

在压缩感知重构算法中，不动点连续(FPC)算法的收敛速度较慢，为解决这个问题，本文引入线性搜索步长，选择步长参数序列{tn}，利用前两次迭代结果的特定线性组合值来计算当前的迭代值，加速算法的收敛速度，从而提出了一种快速不动点连续(FFPC)算法。然后，通过对一维信号进行仿真实验，验证了FFPC算法的收敛性。另外，对于视频帧进行重构的对比实验结果，一方面表明FFPC算法提高了收敛速度，另一方面表明FFPC算法的重构速率明显加快，重构质量也有所提升。因此，FFPC算法是一种快速高效的重构算法。

[1]DONOHODL.Compressedsensing[J].IEEEtransationsoninformationtheory，2006，52(4)：1289-1306.

[2]卢雁，吴盛教，赵文强. 压缩感知理论综述[J]. 计算机与数字工程，2012，40(8)：12-14.

[3]NEEDELLD，TROPPJA.CoSaMP：iterativesignalrecoveryfromincompleteandinaccuratesamples[J].Applied&computationalharmonicanalysis，2008，26(12)：93-100.

[4]BLUMENSATHT，DAVIESME.Iterativethresholdingforsparseapproximations[J].Journaloffourieranalysis&applications，2008，14(5)：629-654.

[5]HALEET，YINW，ZHANGY.Fixed-pointcontinuationforl1-minimization：methodologyandconvergence[J].Siopt，2008，19(3)：1107-1130.

[6]BIOUCAS-DIASJM，FIGUEIREDOMAT.AnewtwIst：two-stepiterativeshrinkage/thresholdingalgorithmsforimagerestoration[J].IEEEtransactionsonimageprocessing，2007，16(12)：2992-3004.

[7]NESTEROVY.Gradientmethodsforminimizingcompositefunctions[J].Mathematicalprogramming，2013，140(3)：768-785.

[8]YAMAGISHIM，YAMADAI.Over-relaxationofthefastiterativeshrinkage-thresholdingalgorithmwithvariablestepsize[J].Inverseproblems，2011，27(10)：8-22.

[9]CANDESEJ，ROMBERGJ.Quantitativerobustuncertaintyprinciplesandoptimallysparsedecompositions[J].Foundationsofcomputationalmathematics，2006，6(2)：227-254.

[10]YINW，OSHERS，GOLDFARBD，etal.BregmaniterativealgorithmsforL1-minimizationwithapplicationstocompressedsensing[J].Siamjournalonimagingsciences，2008(1)：143-168.

[11]HALEET，YINW，ZHANGY.Afixed-pointcontinuationmethodfor'1-regularizedminimizationwithapplicationstocompressedsensing[J].CaamTr，2007(1)：1-43.

[12]CHAMBOLLEA，DOSSALC.Ontheconvergenceoftheiteratesofthe“fastiterativeshrinkage/thresholdingalgorithm”[J].Journalofoptimizationtheory&applications，2015(6)：1-15.

[13]谢志鹏. 基于前向后向算子分裂的稀疏信号重构[J]. 南京大学学报(自然科学版)，2012，48(4)：7-15.

[14]WUG，LUOS.Adaptivefixed-pointiterativeshrinkage/thresholdingalgorithmforMRimagingreconstructionusingcompressedsensing[J].Magneticresonanceimaging，2014，32(4)：372-378.

郭青青(1991— )，女，硕士生，主研压缩感知重构算法及其应用，为本文通信作者；

李雷(1958— )，硕士生导师，教授，主研压缩感知稀疏和重构算法、深度学习等。

责任编辑：时雯

Reconstruction algorithm of compressed sensing based on fast fixed point continuation

GUO Qingqing，LI Lei

(CenterofComputingandApplicationforVisualCognitive，NanjingUniversityofPostsandTelecommunications，Nanjing210046，China)

Fixed Point Continuation (FPC) algorithm is a developed version of convex optimization algorithm，which is an important research method for reconstruction of Compressed Sensing (CS). In this paper，a fast FPC (FFPC) algorithm is proposed to accelerate the convergence speed of FPC algorithm. A linear search step is introduced，and then an efficient coefficient of shifting step is chosen，finally current iteration is updated by using special linear combination of two previous iterations，so the accuracy of each iteration is improved， and hence the convergence speed is accelerated. On the one hand，the convergence of FFPC algorithm has been proved in the experiment， on the other hand，the simulation experiments show that the convergence speed of FFPC algorithm is obviously improved，and the reconstruction quality is better than other algorithms.

convex optimization algorithm；compressed sensing；fast fixed point continuation

TN911

ADOI：10.16280/j.videoe.2016.10.002

国家自然科学基金项目(61501251；61071167)；江苏省普通高校研究生科研创新计划项目(KYZZ15_0236)；南京邮电大学引进人才科研启动基金项目(NY214191)

2016-02-26

文献引用格式：郭青青，李雷.基于快速不动点连续的压缩感知重构算法[J].电视技术，2016，40(10)：6-10.

GUO Q Q，LI L.Reconstruction algorithm of compressed sensing based on fast fixed point continuation[J].Video engineering，2016,40(10)：6-10.