航空弧齿锥齿轮轮齿应力谱精确获取及分布估计*

王延忠，吴朝阳，卞　勇，刘　旸

(1.北京航空航天大学 机械工程及自动化学院, 北京 100191；2.中国兵器工业新技术推广研究所，北京 100089)



航空弧齿锥齿轮轮齿应力谱精确获取及分布估计*

王延忠1，吴朝阳1，卞勇2，刘旸1

(1.北京航空航天大学 机械工程及自动化学院, 北京 100191；2.中国兵器工业新技术推广研究所，北京 100089)

航空弧齿锥齿轮在服役过程中，工况恶劣，振动冲击多，工作过程中的轮齿随机应力谱分布规律对弧齿锥齿轮的设计和寿命预测具有重要作用。根据弧齿锥齿轮动力学模型，计算各工况下的动载系数，建立综合考虑支持刚度变形和动载荷的弧齿锥齿轮加载接触分析有限元模型，通过计算和处理得到弧齿锥齿轮工作过程中的齿面接触应力谱和齿根弯曲应力谱样本，进而利用混合正态分布参数估计法对轮齿随机应力谱分布进行估计。

弧齿锥齿轮;动载荷;支承刚度变形;加载接触分析;轮齿随机应力谱分布

航空弧齿锥齿轮是直升机传动系统中最重要、最复杂和最薄弱的动力元件。其常处在高速、重载条件下工作，工况恶劣，振动冲击多，由齿轮失效导致的后果往往是灾难性的。精确获取齿面应力谱的分布规律对航空弧齿锥齿轮传动系统的设计和寿命预测具有重大意义。

为了研究弧齿锥齿轮的轮齿随机应力谱分布，就有必要对齿轮应力进行分析。目前，齿轮应力计算分析通常是利用LTCA有限元法[1-2]；但这是建立在静力分析基础上，并未考虑动力因素的影响。由于啮合刚度的时变性和制造误差而产生的振动和冲击，使得齿轮传递的载荷远大于静态载荷，国内外研究学者通常利用集中参数法建立多自由度的齿轮振动模型,进而通过数值方法进行求解[3-4]。

本文根据航空弧齿锥齿轮传动系统的功率谱，通过对弧齿锥齿轮动力学模型进行数值求解获取动载荷系数；建立弧齿锥齿轮加载接触分析有限元模型，将动载系数以及支承刚度和轴系变形量作为有限元模型的边界条件输入，精确获取各个工况下的轮齿应力，结合各工况时间比对轮齿应力进行扩展，得到齿面整个工作过程的随机应力数据样本；最后利用混合正态分布参数法进行估计，得到弧齿锥齿轮整个工作过程中的轮齿随机应力谱分布规律。

1　弧齿锥齿轮系统参数和功率谱

弧齿锥齿轮的参数见表1。弧齿锥齿轮工作功率谱见表2。其中，时间百分比η为该工况运行时间占所有工况运行时间和的比例。

表1　齿轮相关参数

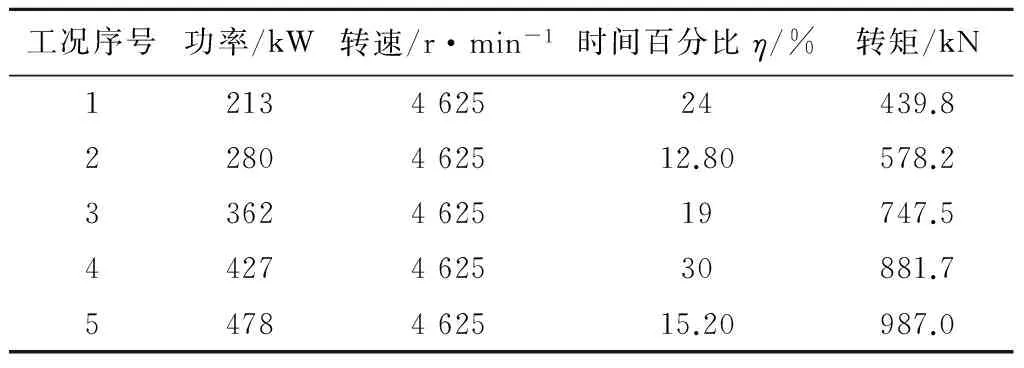
表2　弧齿锥齿轮传动系统输入功率谱

2　各工况下的弧齿锥齿轮动载系数获取

2.1动力学数学模型的建立

在齿轮动力学模型中(见图1)，两齿轮用集中质量和集中转动惯量来模拟，轴模拟成无质量的刚体，用弹簧和阻尼器来模拟，轮齿啮合刚度用一对弹簧和阻尼器模拟。

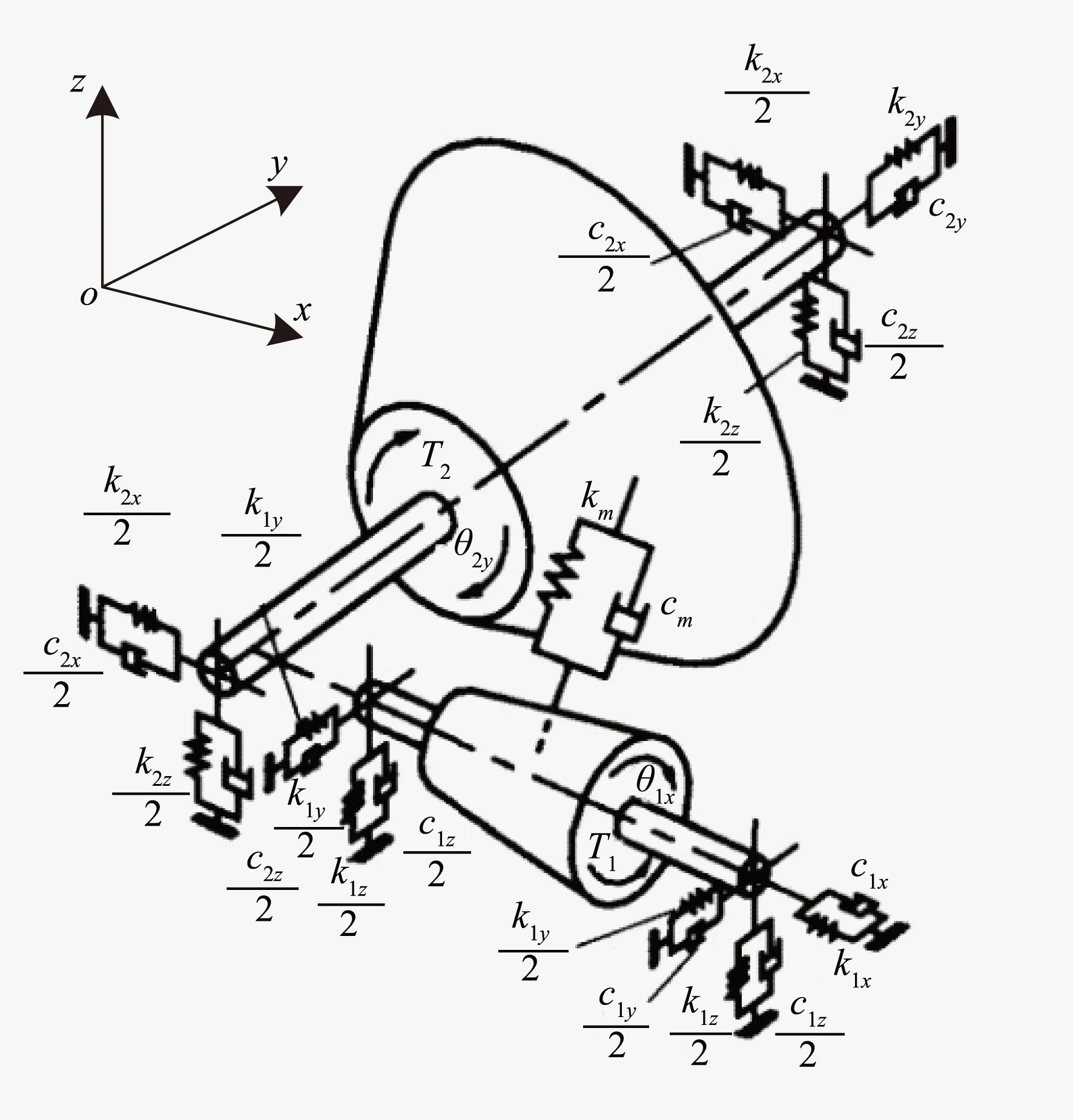
图1　弧齿锥齿轮动力学模型

弧齿锥齿轮传动系统可以等效为八自由度的动力学模型，系统的自由度表示为列向量：

q={X1,Y1,Z1,θ1x,X2,Y2,Z2,θ2y}T

式中，Xi、Yi和Zi(i=1,2) 分别为齿轮沿x轴、y轴移动和z轴横向振动位移；θ1x、θ2y分别为主动齿轮绕x轴、被动齿轮绕y轴的扭转振动位移。

齿面啮合点间由于振动和误差产生的沿啮合点法线方向的相对位移为：

λn=(x1-x2)a1-(y1-y2)a2-

式中，a1=cosδ1sinαn；a2=cosδ1cosαnsinβ1，a3=cosαncosβ1；en(t)为齿轮副的法向静态误差；δ1为主动轮的节锥角；αn为法面压力角；β1为主动轮的中点螺旋角；r1、r2为两齿轮啮合点半径。

齿形误差通常用正弦简谐函数表示：

en(t)=e0+ercos(Ωht+φ)

式中，e0、er为轮齿误差的常值和幅值，通常取e0=0；Ωh为齿轮的啮合频率；φ为相位角，通常取φ=0。

齿轮副在啮合时的法向动载荷及沿坐标方向的分力如下：

啮合刚度取为：

式中，ch为啮合阻尼；km为啮合刚度的平均值；Akl为刚度的l阶谐波幅值；Φkl为刚度的l阶初相位。弧齿锥齿轮的啮合刚度可以根据LTCA原理获取并进行公式拟合[5]。根据经验公式，齿轮啮合阻尼为：

式中，J1，J2分别为主、从动轮的转动惯量；R1，R2分别为主、从动轮的基圆半径；ξg为轮齿啮合阻尼比，本文取ξg=0.1。

弧齿锥齿轮传动系统的振动微分方程组为：

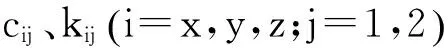
将λn作为新的自由度，消去θ1x和θ2y，系统的自由度数由8个降为7个，合并后的方程为：

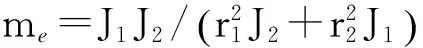
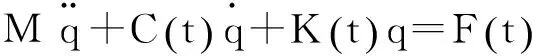
做如下变换：

引入状态变量：

将上式中的7个二阶微分方程变为14个一阶微分方程，可以通过龙格库塔数值积分法进行求解。

2.2动载系数的求解

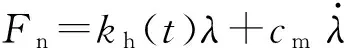
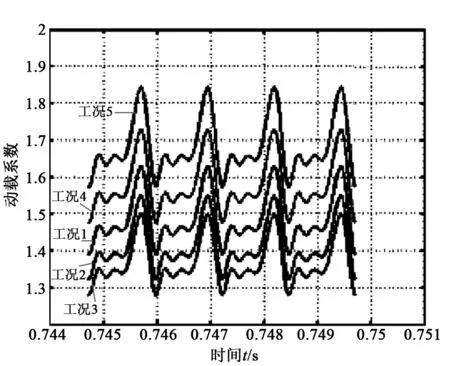
图2　不同工况下齿轮的动载系数

从图2中工况1～工况3可以看出，保持齿轮的转速不变，随着转矩的增加，弧齿锥齿轮的动载系数减小，这是因为随着载荷的增大，弧齿锥齿轮的传动比增大，传动误差变小，传动更加平稳；由工况4和工况5可以看出，弧齿锥齿轮的动载系数随着载荷的增大而增大，这是因为当载荷超过一定范围后，齿轮的动态冲击激励占主导作用，随着载荷的增大，齿轮的动态冲击激励变大，因而，弧齿锥齿轮的动载系数增大。

3　考虑动载荷和支承刚度的轮齿应力获取

3.1有限元模型的建立

由于动力学因素的影响，弧齿锥齿轮的实际工作载荷会比额定载荷增大；同时弧齿锥齿轮传动系统在载荷作用下，轴承支承和轴系会发生变形，致使齿轮的啮合位置发生变化，这些因素都在不同程度上影响了弧齿锥齿轮的传动性能。为了提高弧齿锥齿轮的轮齿应力的计算结果准确性，应考虑弧齿锥齿轮传动系统的动力学因素和支承刚度变形的影响。

结合弧齿锥齿轮的加载接触有限元分析原理，建立该对考虑动力学因素和支承刚度变形的弧齿锥齿轮加载接触分析有限元模型，大小轮设置同样的材料属性：弹性模量为210 GPa，泊松比为0.3。空间问题中对计算对象形状适应较好的是四面体单元，四面体单元对边界拟合的能力强；因此，本文选择四面体单元C3D10进行网格划分。划分网格后的有限元模型如图3所示。

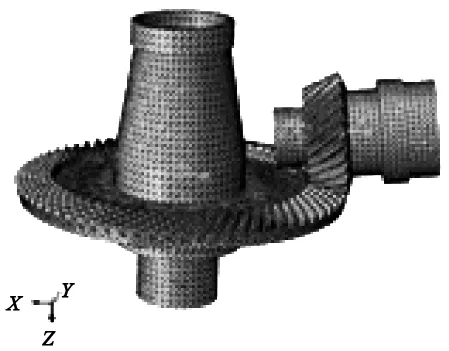
图3　四面体单元C3D10划分网格后的模型

轴承刚度采用弹簧进行模拟(见图4)，将轴承支承面与参考点RP-pp-1在x,y和z方向的平移自由度进行耦合，然后将参考点采用“Spring>Creat>Connect points to ground”命令与空间固定点连接起来，设置弹簧的x、y和z方向的刚度值。

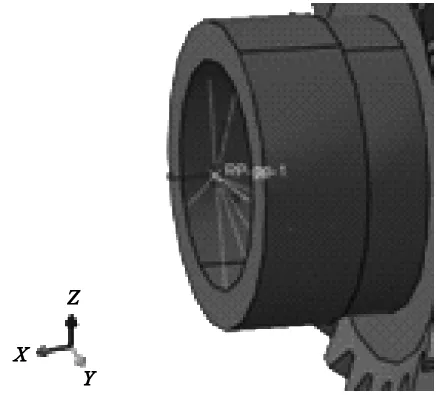
图4　轴承刚度模拟

本文中的弧齿锥齿轮在传动过程中发生二、三齿啮合交替变化，一个轮齿啮合周期历程中的动载系数变化如图5所示。根据轮齿的啮合位置，将ABAQUS软件中的Amplitude幅值曲线设置成相应的动载系数。分别设定5个工况的载荷大小，提交Job，进行计算分析。

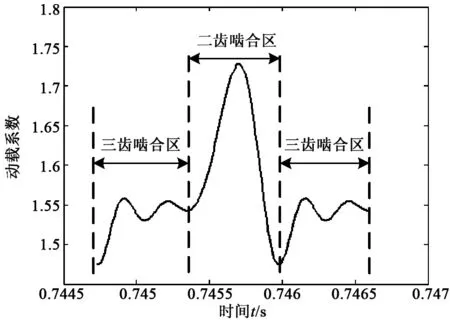
图5　一个啮合周期历程中的动载系数变化

3.2有限元计算结果

图6～图10分别为5个工况有限元计算结果的齿面中点接触应力和齿根中点弯曲应力在啮合过程中的曲线变化图，其中，曲线1、曲线2分别为不考虑和考虑动载系数的应力计算结果。

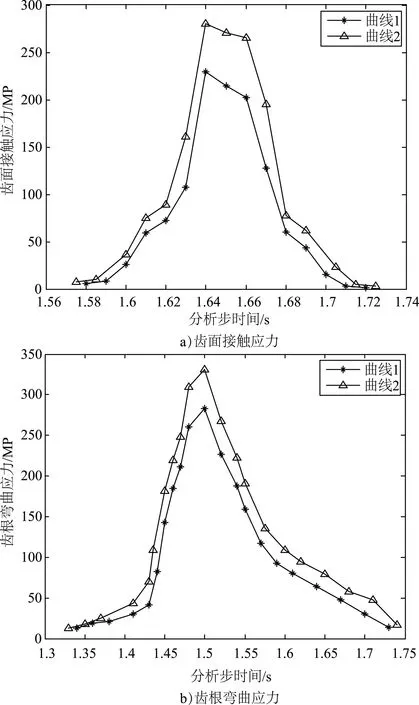
图6　工况1的齿面接触应力和齿根弯曲应力

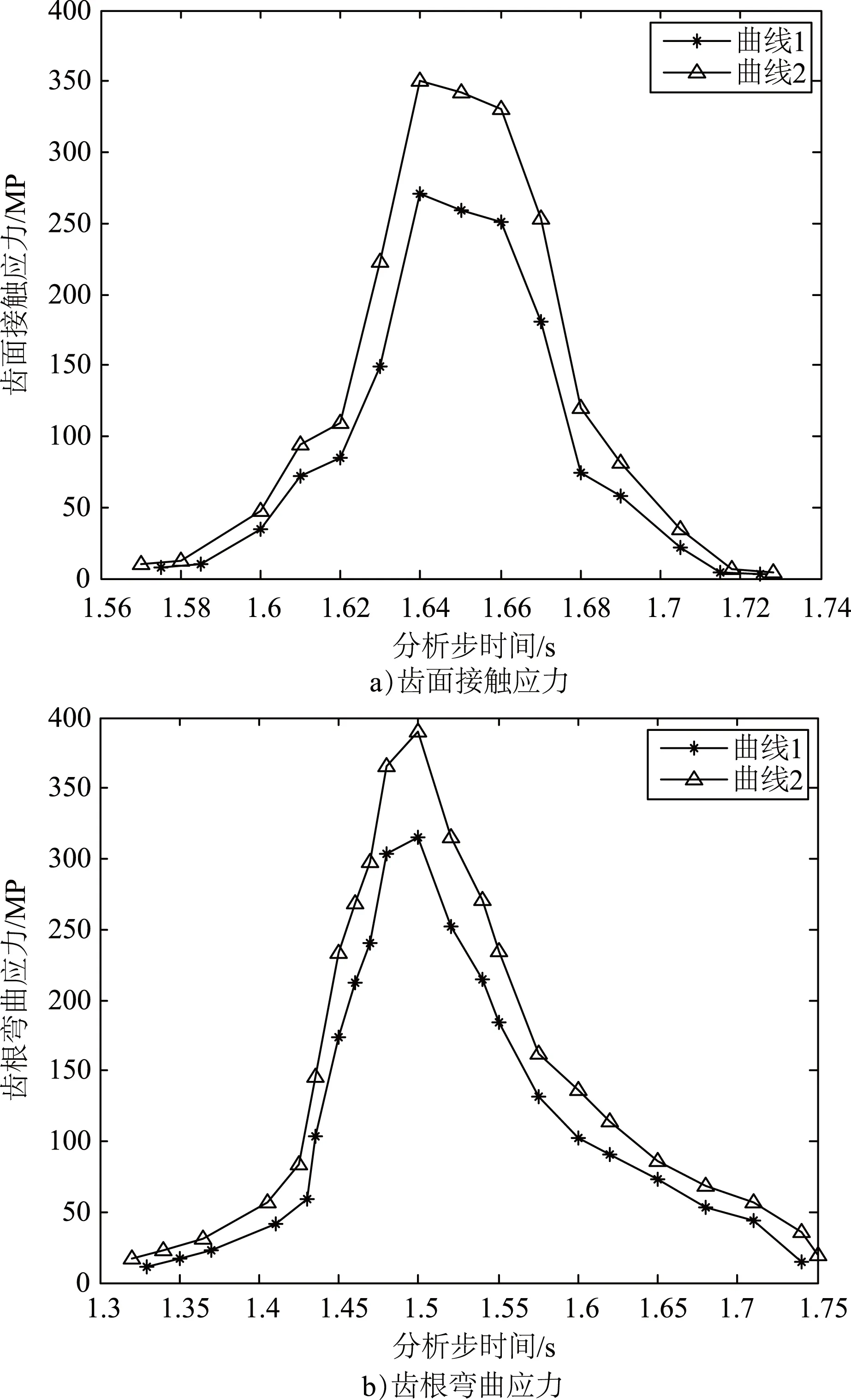
图7　工况2的齿面接触应力和齿根弯曲应力

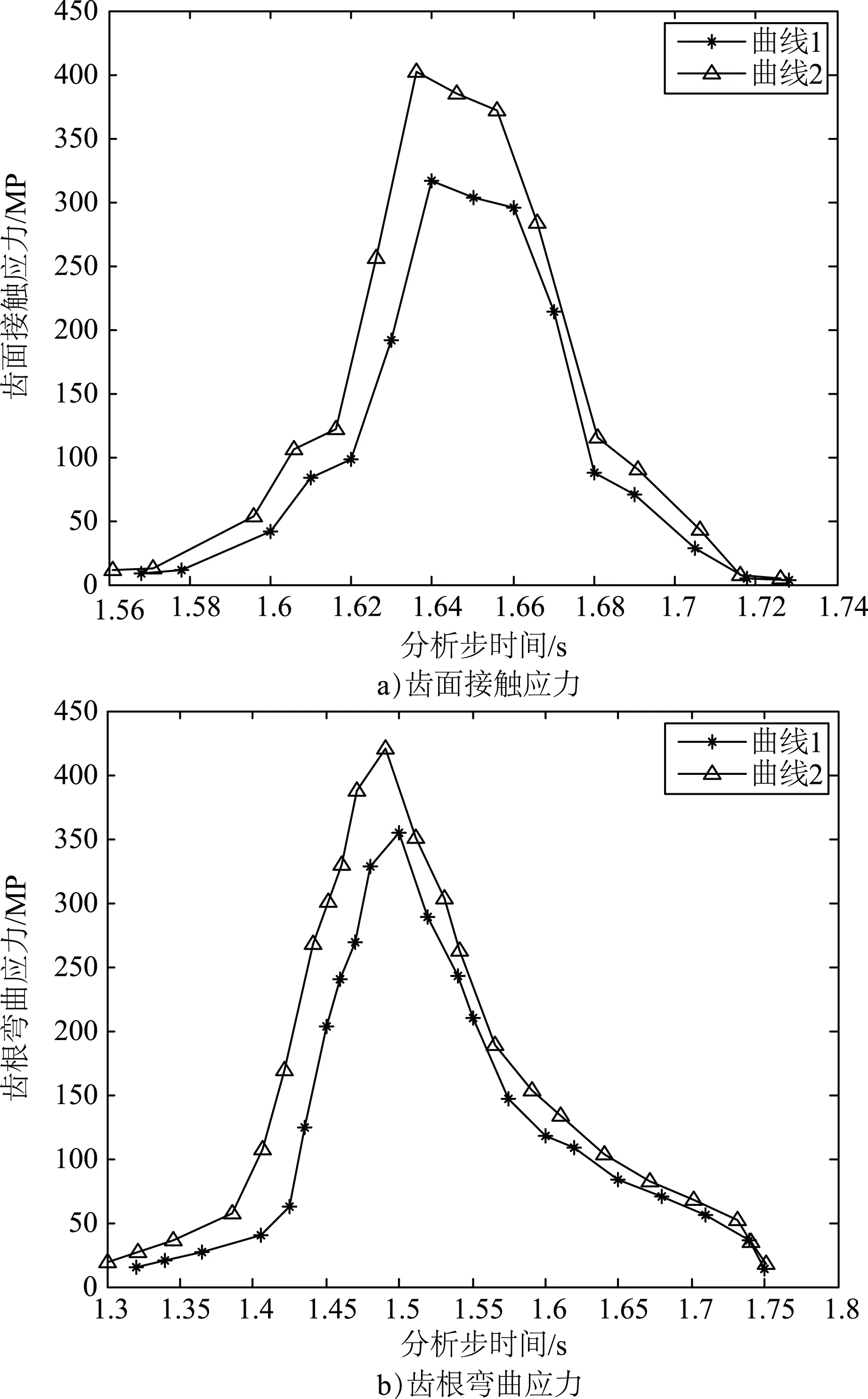
图8　工况3的齿面接触应力和齿根弯曲应力

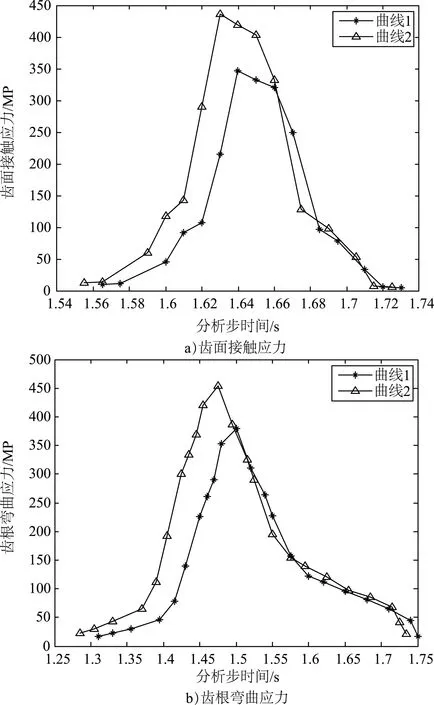
图9　工况4的齿面接触应力和齿根弯曲应力

图10　工况5的齿面接触应力和齿根弯曲应力

由图6～图10可知，考虑动载系数的弧齿锥齿轮有限元模型会使轮齿载荷增大，齿面接触应力和齿根弯曲应力都会相应地提升，受载时间也会变长；由于考虑支承刚度和轴系变形，轮齿在受载情况下会明显发生提前啮合，轮齿啮合位置发生改变，进而会影响轮齿的应力值，因此，考虑动载系数和支承刚度变形的应力计算结果会更精确。

将各工况下提取的齿面接触应力值和齿根弯曲应力值扩展该工况的时间百分比η×104次，然后将各工况扩展后的齿面接触应力和齿根弯曲应力值分别进行叠加，得到弧齿锥齿轮整个工作过程中的齿面接触应力和齿根弯曲应力数据样本。

4　轮齿应力谱统计及分布估计

为了对弧齿锥齿轮传动系统的设计与寿命预测，就需要得到该弧齿锥齿轮传动系统的轮齿应力谱的总体分布规律；因此，有必要对应力数据进行处理和统计。传统的统计方法一般假设应力谱数据来自于某种分布的样本，然后进行研究推断；但是由于数据形态面临越来越复杂的趋势，很多情况下不同的局部表现出不同的特性，利用单一参数分布族函数将带来较大的偏差，现在比较成熟的有混合分布模型分析法[6-7]。混合分布模型是由K. Person提出的，随着计算机事业的蓬勃发展，计算能力不断提高，混合分布已经成为数据处理和统计的一个重要工具，并得到了广泛的应用。

本文先对轮齿应力数据进行载荷等级分组，然后统计各载荷等级的帧数以及概率密度，最后利用混合正态分布法对轮齿应力谱进行分布估计。混合正态分布模型概率密度函数为：

式中，w-li为各正态分布的权重系数；μi为各正态分布的期望；σi为各正态分布的标准差；l为需要估计的正态分布的个数。具体数据处理流程如图11所示。

编制相应的计算程序，对弧齿锥齿轮整个工作过程中的齿面接触应力谱和齿根弯曲应力谱样本进行处理，得到轮齿随机应力谱的总体分布结果(见图12和图13)。

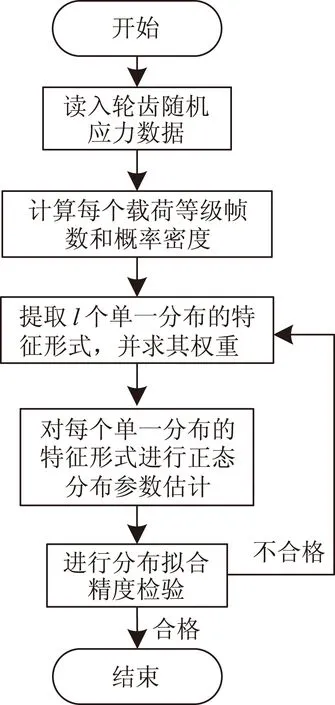
图11　流程图

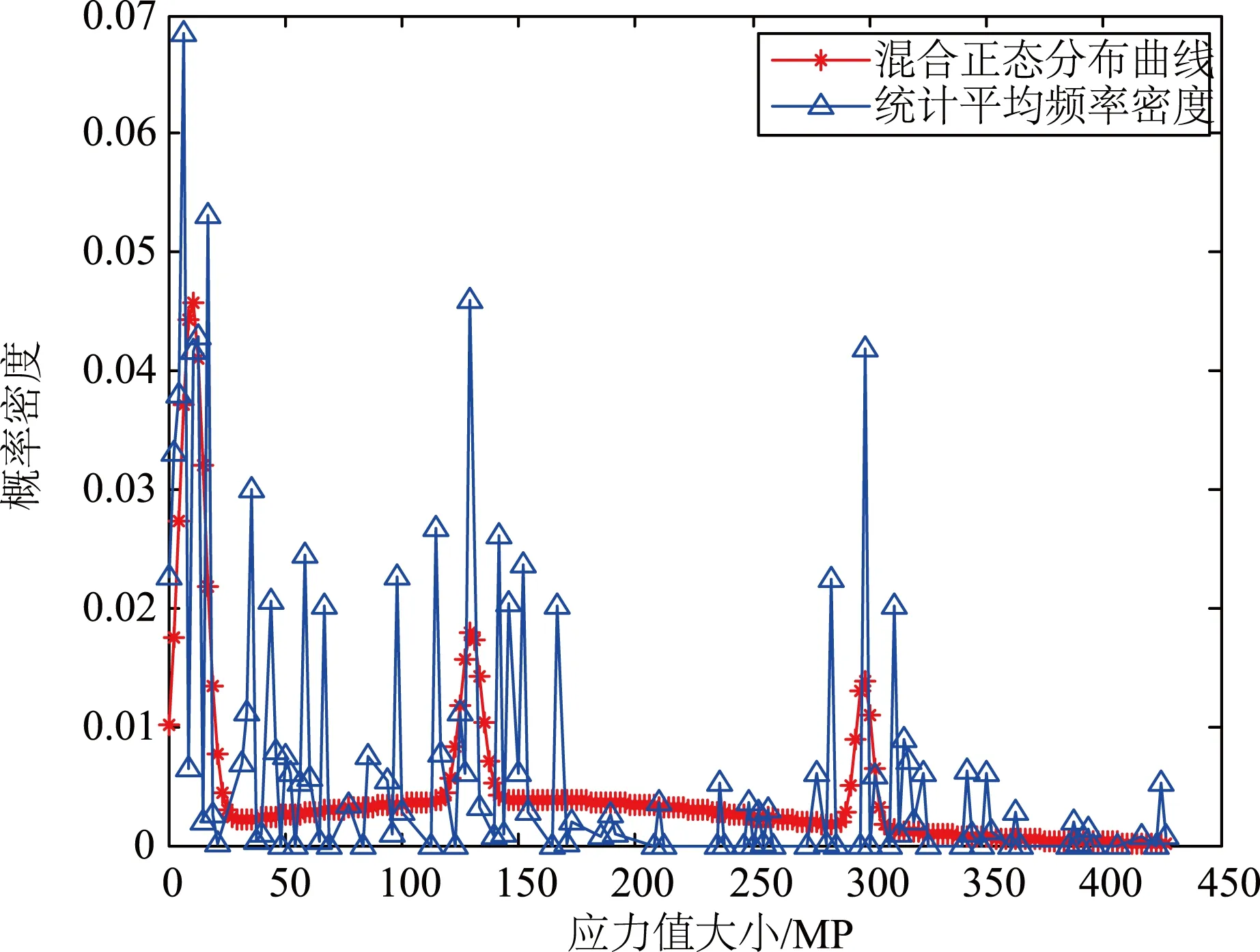
图12　齿面接触应力谱分布

由图12可知，齿面接触应力谱的分布为：w-l1=0.335，μ1=10，σ1=5.4；w-l2=0.079，μ2=129.3，σ2=4.5；w-l3=0.532，μ3=148.6，σ3=107；w-l4=0.054，μ4=298，σ4=3.5。

由图13可知，齿根弯曲应力谱的分布为：w-l1=0.247，μ1=50.6，σ1=20.5；w-l2=0.183，μ2=215.5，σ2=22.7；w-l3=0.165，μ3=500.1，σ3=23.5；w-l4=0.405，μ4=266.9，σ4=95.1。

5　结语

通过上述分析，得到如下结论。

1)通过建立弧齿锥齿轮动力学模型，计算得到了某弧齿锥齿轮系统的各工况下的动载系数。

2)建立了一种综合考虑动力学因素和支承刚度变形影响的弧齿锥齿轮的加载接触分析有限元模型，计算结果表明，综合考虑动力学因素和支承刚度变形，轮齿在受载情况下会明显发生提前啮合，齿根弯曲应力和齿面接触应力会增大，受载时间也会变长。

3)基于某弧齿锥齿轮传动系统的功率谱，通过计算分析得到弧齿锥齿轮整个工作过程中的齿面接触应力和齿根弯曲应力数据样本，并基于混合正态分布参数估计法对轮齿应力数据进行处理，得到了轮齿随机应力谱的分布，为弧齿锥齿轮的设计和寿命预测提供了重要依据。

[1] 王延忠,刘溢溥,张祖智,等. 重载弧齿锥齿轮承载特性分析[J]. 新技术新工艺，2014(1)：60-63.

[2] 唐进元,陈嫦,蒲太平，等.考虑误差、轴变形和轴承刚度的弧齿锥齿轮LTCA[J].机械传动，2010，34(5)：5-8.

[3] 王立华, 黄亚宇, 李润方, 等. 弧齿锥齿轮传动系统的非线性振动特性研究[J]. 中国机械工程, 2007，18(3)：260-264.[4] 王三民, 沈允文, 董海军. 含间隙和时变啮合刚度的弧齿锥齿轮传动系统非线性振动特性研究[J]. 机械工程学报, 2003，39(2)：28-32.

[5] 唐进元, 蒲太平.基于有限元法的螺旋锥齿轮啮合刚度计算[J].机械工程学报, 2011，47(11)：23-29.

[6] Pearson K. Contributions to the theory of the mathematieal evolution [J].Philosophieal Transaetions of the Royal Soeiety of London，1894，185：71-110.

[7] Nagode M F M.On a new method for prediction of the scatter of loading spectra[J].International Journal of Fatigue，1998，20(4)： 271-277.

*国家自然科学基金资助项目(51275020)

国家高科技支撑项目(2014BAF08B01)

航空A计划项目(ATR-125-02-101)

责任编辑马彤

Precise Acquisition and Distribution Estimation of Tooth Random Stress Spectrum of Aviation Spiral Bevel Gear

WANG Yanzhong1, WU Zhaoyang1, BIAN Yong2, LIU Yang1

(1.School of Mechanical Engineering and Automation Beihang University， Beijing 100191， China；2.Chinese Advanced Technology Generalization Institute of CNGC， Beijing 100089， China)

Aviation spiral bevel gear is working under severe conditions which are full of vibration and impact. Tooth random stress distribution is important for spiral bevel gear design and life prediction. The loaded contact analysis with finite element model of spiral bevel gear is established, considering deformation of support stiffness and dynamic load, which is calculated based on the dynamic model. Samples of tooth contact stress and tooth root bending stress spectrum are obtained. Then use the mixed normal distribution parameter method to estimate the distribution of tooth stress spectrum.

spiral bevel gear，dynamic load，deformation of support stiffness，loaded contact analysis，distribution of tooth random stress spectrum

TH 132.41

A

王延忠 (1963-),男，教授，主要从事先进精密传动加工技术等方面的研究。

2016-04-02