牵引变压器悬挂系统静刚度设计研究*
张远亮
(四川城市职业学院 汽车与信息工程学院, 四川成都 610110)
综合技术研究
牵引变压器悬挂系统静刚度设计研究*
张远亮
(四川城市职业学院 汽车与信息工程学院, 四川成都 610110)
针对车体与车下悬挂设备牵引变压器之间的隔振器刚度设计问题,对牵引变压器悬挂系统进行模型简化,得到关于牵引变压器的力和力矩平衡方程。同时再根据变压器隔振器6点共平面条件得到几何约束协调方程,得出了给定隔振器静挠度条件下设计隔振器刚度以及给定隔振器刚度条件下计算各个隔振器的静挠度的方法。对某动车牵引变压器静刚度进行实例设计。确定隔振器刚度工况,计算出了各工况下每个隔振器的静挠度值。考虑各个隔振器静挠度差,得到满足各个隔振器静挠度差均在1 mm范围内对应的各个隔振器静刚度;考虑每个隔振器静挠度在6~7 mm范围内的设计目标,得到各个隔振器的静刚度以及对应的静挠度。
牵引变压器;刚度设计;静刚度;静挠度
牵引变压器等设备直接悬挂于车体下方,这些设备通常重达6~7 t,且往往具有复杂的自身振动源。随着动车组不断提速以及车体轻量化的技术改进设计,车下悬挂设备如牵引变压器等振动加剧,同时加剧了车体振动,降低车辆舒适度,使旅客乘座舒适感明显降低[1-3]。更严重情况下会导致车体与悬挂设备之间的隔振器产生裂纹、脱落等严重后果,酿成车辆运行安全事故。
西南交通大学吴会超[4-5]利用动力学基本理论,研究了动车组悬挂设备对车辆系统动力学性能指标的影响规律。以车下设备牵引变压器为例,对比了弹性悬挂以及刚性悬挂对橡胶隔振器疲劳寿命的作用,得出了在隔振器承受载荷情况以及隔振器的疲劳寿命方面,弹性悬挂均比刚性悬挂更好的结论。西南交通大学石怀龙、邬平波等[6-7]建立了高速动车组车辆刚柔耦合动力学模型,采用动态扫频法,阐述计算了悬挂设备质量、垂向悬挂刚度、悬挂阻尼以及设备纵向悬挂位置对车体及设备振动的关系;同时也进一步探究了不同参数彼此的动态影响特性。
同济大学宫岛[8-9]等在建立包含悬挂设备的车辆系统垂向刚柔耦合动力学模型的基础上,给出了动车组悬挂设备橡胶隔振器垂向刚度值,并阐述了隔振器垂向刚度、阻尼比、设备安装位置和设备的质量对悬挂设备振动以及动车组运营舒适度的作用规律。
关于牵引变压器悬挂刚度的研究,仅集中在悬挂刚度、阻尼比、变压器质量、安装位置对车辆系统动力学方面的影响。
介绍了牵引变压器悬挂静刚度的设计方法。对变压器悬挂系统进行模型简化,得到关于变压器的平衡方程。同时再根据变压器隔振器6点共平面条件得到几何约束协调方程,得出了给定隔振器静挠度条件下设计隔振器刚度、给定隔振器刚度条件下计算各个隔振器的静挠度的方法。对某动车牵引变压器静刚度进行实例设计。对工程中静刚度设计具有指导意义。
1 静刚度设计基本方法
根据牵引变压器几何参数,画出牵引变压器6个隔振器位置示意图,同时对变压器悬挂系统简化模型进行分析,如图1所示。

图1 变压器悬挂系统简化模型
研究分析的车型为CRH2型中某改进动车组,该动车组的基本物理参数及几何参数见表1和表2。
根据力和力矩平衡得到以下方程:
力平衡方程:
F1+F2+F3+F4+F5+F6=Mg
(1)

表1 牵引变压器模型物理参数
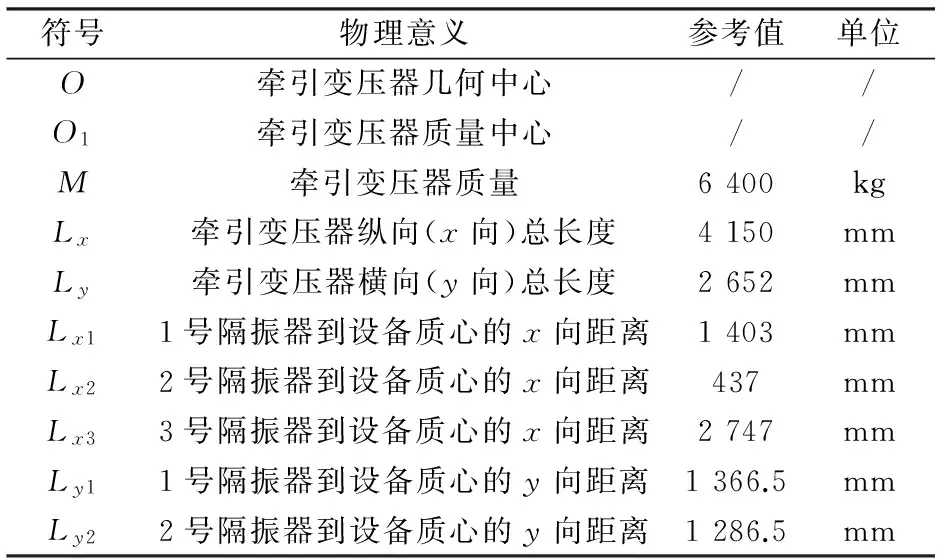
表2 牵引变压器模型几何参数
力矩平衡方程(K1和K3所在直线力矩平衡):
(2)
力矩平衡方程(K1和K4所在直线力矩平衡):
(3)
根据图1,以牵引变压器几何中心为坐标原点建立坐标系,得到6个隔振器的坐标位置。具体结果见表3。

表3 6个隔振器坐标位置
变压器设备通常重达6~7 t,一般安装于车体下方中部位置。考虑车体对称性,本文简化考虑,假设变压器上方车体变形挠度均相等。根据牵引变压器隔振器6点共平面条件得到几何约束协调方程。以1号、3号及6号隔振器坐标位置建立平面。假设平面方程为式(4):
Ax+By+Cz=1
(4)
式中A、B、C为平面方程的系数。
将表3中1号、3号、6号隔振器坐标带入平面方程式(4),得到平面方程系数:
(5)
(6)
(7)
将2号、4号及5号隔振器坐标代入式(4),同时联立方程组见式(5)~式(7),得到Z2、Z4、Z5与Z1、Z3和Z6的显示关系。因篇幅原因,这里具体表达式不再给出。
将Z1、Z2、Z3、Z4、Z5及Z6分别代入平面约束方程式(4),化简得静挠度的几何约束关系:
(8)
根据胡克定律得到橡胶隔振器变形量与受力的关系:
(9)
1.1给定隔振器静挠度条件下设计隔振器刚度
当给定1号、3号及6号隔振器的静挠度Z1、Z3、Z6时,将Z1、Z3、Z6代入平面约束显示关系式,得到2号、4号及5号隔振器的静挠度Z2、Z4、Z5,
从隔振器的实际运用中互换性、经济性等方面的考虑,计算中令:
K1=K4,K2=K5,K3=K6。
结合式(1)~式(3),该方程组是关于K1,K2,K3,K4,K5,K6为变量的方程,求解方程得到每个隔振器的刚度值。方程组见式(10)。
(10)
其中:K1,K2,K3,K4,K5,K6为变量;Z1,Z2,Z3,Z4,Z5,Z6为参数(已知量)。
1.2模态给定隔振器刚度条件下计算各个隔振器的静挠度
当给定每个隔振器的刚度时,结合式(1)~式(3)以及平面约束显示关系,该方程组是关于Z1,Z2,Z3,Z4,Z5,Z6为变量的方程,求解方程得到每个隔振器的静挠度。方程组见式(11)。
(11)
其中:Z1,Z2,Z3,Z4,Z5,Z6为变量;K1,K2,K3,K4,K5,K6为参数(已知量)。
2 某动车牵引变压器悬挂系统静刚度设计
利用上节中静刚度设计基本方法,现对CHR2型某动车组牵引变压器悬挂系统静刚度进行设计。牵引变压器悬挂系统简化模型见图1。动车组具体参数见表2。
从隔振器的实际运用中互换性、经济性等方面的考虑,计算中令K1=K4,K2=K5,K3=K6。隔振器刚度的选取是在已有研究基础上[8,10],结合悬挂系统静刚度设计经验得到。各个工况中刚度值依次增加1.2倍。
(1)K1和K4取值范围为:{1 300,1 560,1 872,2 246,2 695,3 234} N/mm
(2)K2和K5取值范围为:{880,1 056,1 267,1 502,1 824,2 189} N/mm
(3)K3和K6取值范围为:{470,564,676.8,812.2,974.6, 1 169.5}N/mm
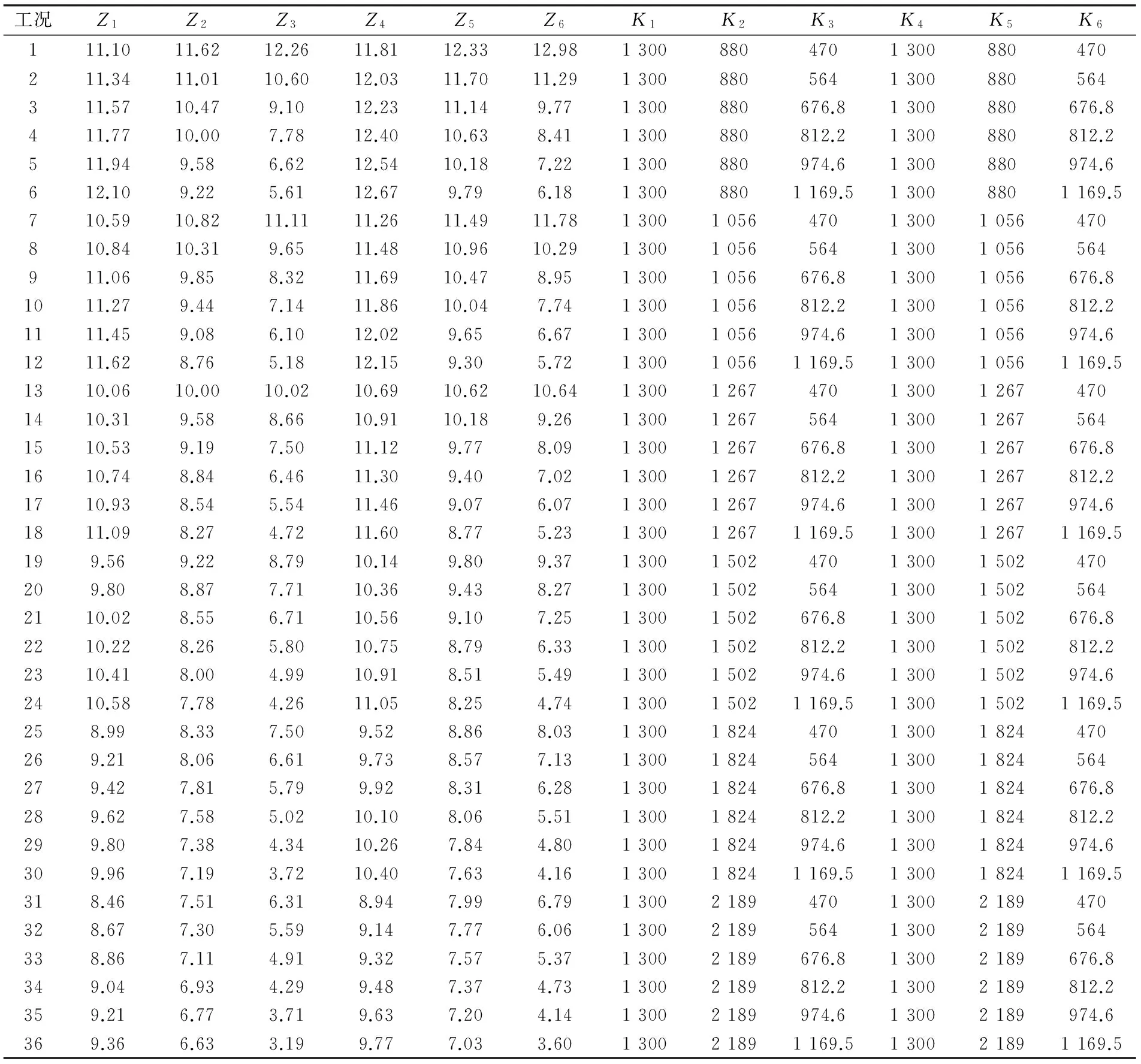
表4 给定隔振器刚度条件下计算各个隔振器的静挠度 Z/mm, K/(N·mm-1)
(4)各个隔振器安装座位于同一个平面内。
牵引变压器静刚度设计目标1:
6个隔振器静挠度均在6~7 mm范围内。
牵引变压器静刚度设计目标2:
6个隔振器静挠度差均在1 mm范围内。
本文仅给出K1(K4)等于1 300,2 246 N/mm静挠度值的情况,其余情况下读者可以自行计算。
2.1刚度K1(K4)为1 300 N/mm时各个工况下的静挠度变化
隔振器刚度K1和K4相等,均为1 300 N/mm,保持不变;隔振器刚度K2和K5相等,取值分别为880,1 056,1 267,1 502,1 824,2 189 N/mm;隔振器刚度K3和K6相等,取值分别为:470,564,676.8,812.2,974.6, 1 169.5 N/mm。
当K1=K4=1 300 N/mm,K2=K5=880 N/mm时,静挠度随静刚度K3、K6变化见图2。

图2 静挠度随静刚度K3、K6变化图
从图2可以得到:当K1=K4=1 300 N/mm,K2=K5=880 N/mm时,
(1)2号、5号、3号及6号隔振器静挠度随着K3、K6刚度的增大而减小,1号及4号隔振器静挠度随着K3、K6刚度的增大而增大;
(2)在此刚度范围内,不存在满足6个隔振器的静挠度均在6~7 mm范围内的设计目标;
(3)根据表4工况1及工况2中Z1静挠度及K3刚度得到2点(470,11.10)及(564,11.34),根据2点式直线公式(12):
(12)
得到直线方程式(13):
Z1=0.002 6×K3+9.900 0
(13)
同理得到其余直线方程(14):
(14)
此工况下不存在Z1~Z6挠度均在6~7 mm范围内的情况;当K3、K6∈(514~543) N/mm时,Z1~Z6挠度差均在1 mm范围内。具体结果见表5。
根据表4得到静刚度与变压器左右拉伸挠度差(Z4-Z1=Z5-Z2=Z6-Z3)的关系,见图3。
从图3可以得到:当K1=K4=1 300 N/mm,K2(K5)刚度分别为880,1 056,1 267,1 502,1 824,2 189 N/mm时,

表5 Z1~Z6挠度差均在1 mm范围内的刚度范围 Z/mm,K/(N·mm-1)
(1)变压器左右拉伸挠度差随隔振器K3(K6)刚度的增加呈减小趋势;
(2)变压器左右拉伸挠度差均大于零,即隔振器Z4、Z5、Z6的拉伸挠度分别大于隔振器Z1、Z2、Z3的拉伸挠度;
(3)变压器Z4(Z5、Z6)侧向下倾斜。
根据表4得到静刚度与变压器前后拉伸挠度差(Z3-Z1=Z6-Z4)的关系,见图4。
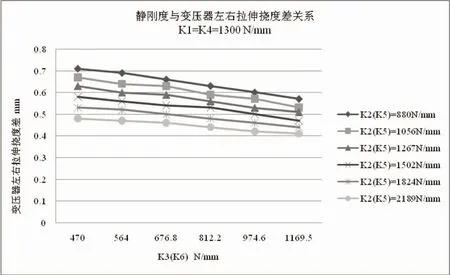
图3 静刚度与变压器左右拉伸挠度差关系
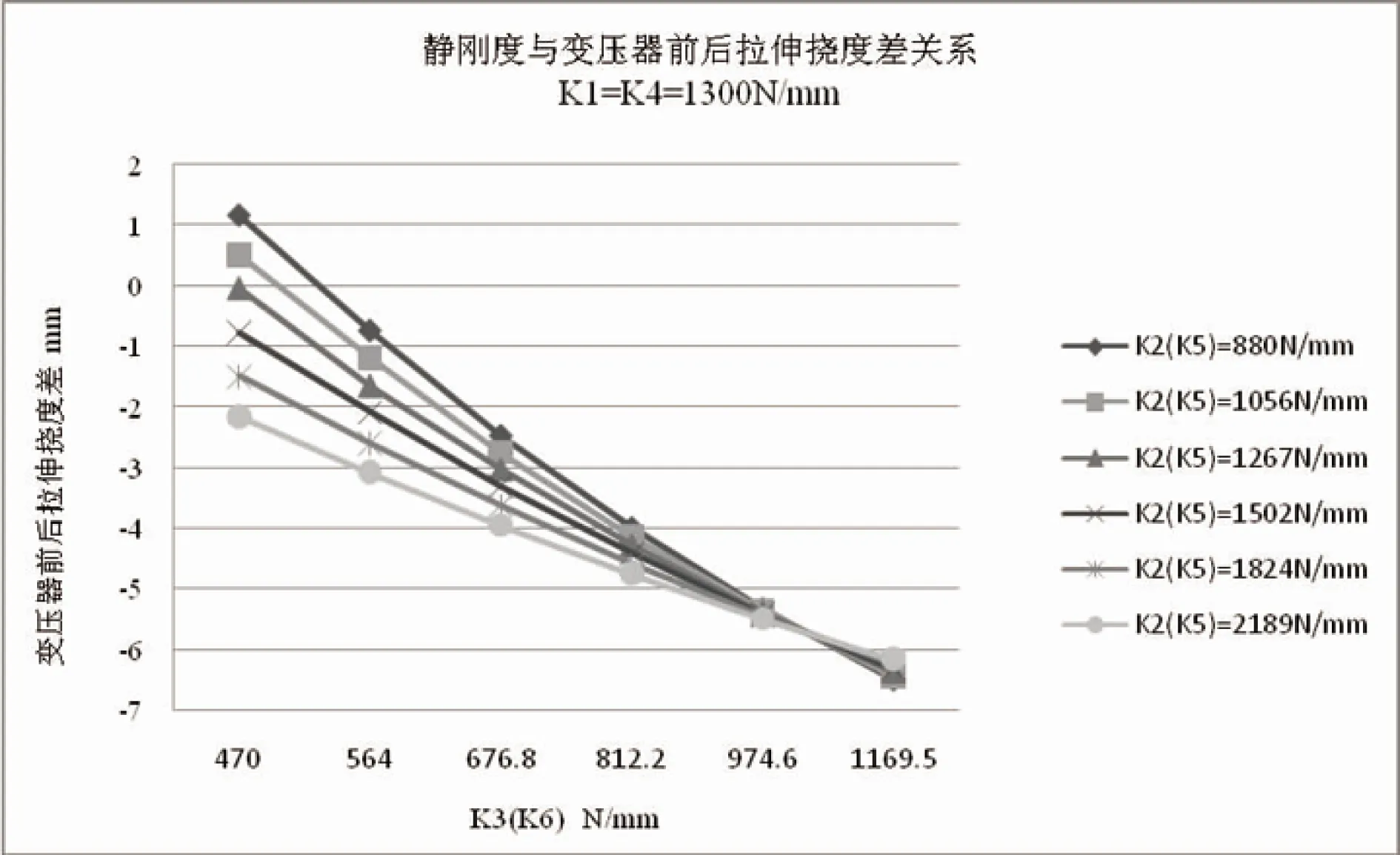
图4 静刚度与变压器前后拉伸挠度差关系
从图4可以得到:
(1)当K1=K4=1 300 N/mm,K2(K5)刚度分别为1 267,1 502,1 824,2 189 N/mm时,
(a)变压器前后拉伸挠度差均小于零,即隔振器Z3、Z6的拉伸挠度分别小于隔振器Z1、Z4的拉伸挠度;
(b)变压器前后拉伸挠度差绝对值随隔振器K3(K6)刚度的增加呈增大趋势;
(c)变压器Z1(Z4)端向下倾斜。
(2)当K1=K4=1 300 N/mm,K2(K5)刚度分别为880,1 056 N/mm时,
(a)变压器前后拉伸挠度差随隔振器K3(K6)刚度的增加由正值变为负值;
(b)根据静挠度差与静刚度线性插值关系,当K2(K5)=880 N/mm,K3(K6)=527 N/mm时,变压器前后拉伸挠度差为零;当K2(K5)=1 056 N/mm,K3(K6)=498 N/mm时,变压器前后拉伸挠度差为零。
2.2刚度K1(K4)为2 246 N/mm时各个工况下的静挠度变化
隔振器刚度K1和K4相等,均为2 246 N/mm,保持不变;隔振器刚度K2和K5相等,取值分别为1 300,1 560,1 872,2 246,2 695,3 234 N/mm;隔振器刚度K3和K6相等,取值分别为:470,564,676.8,812.2,974.6, 1 169.5 N/mm。计算这些工况下各个隔振器的静挠度见表6。
当K1=K4=2 246 N/mm,K2=K5=1 502 N/mm时,静挠度随静刚度K3、K6变化见图5。
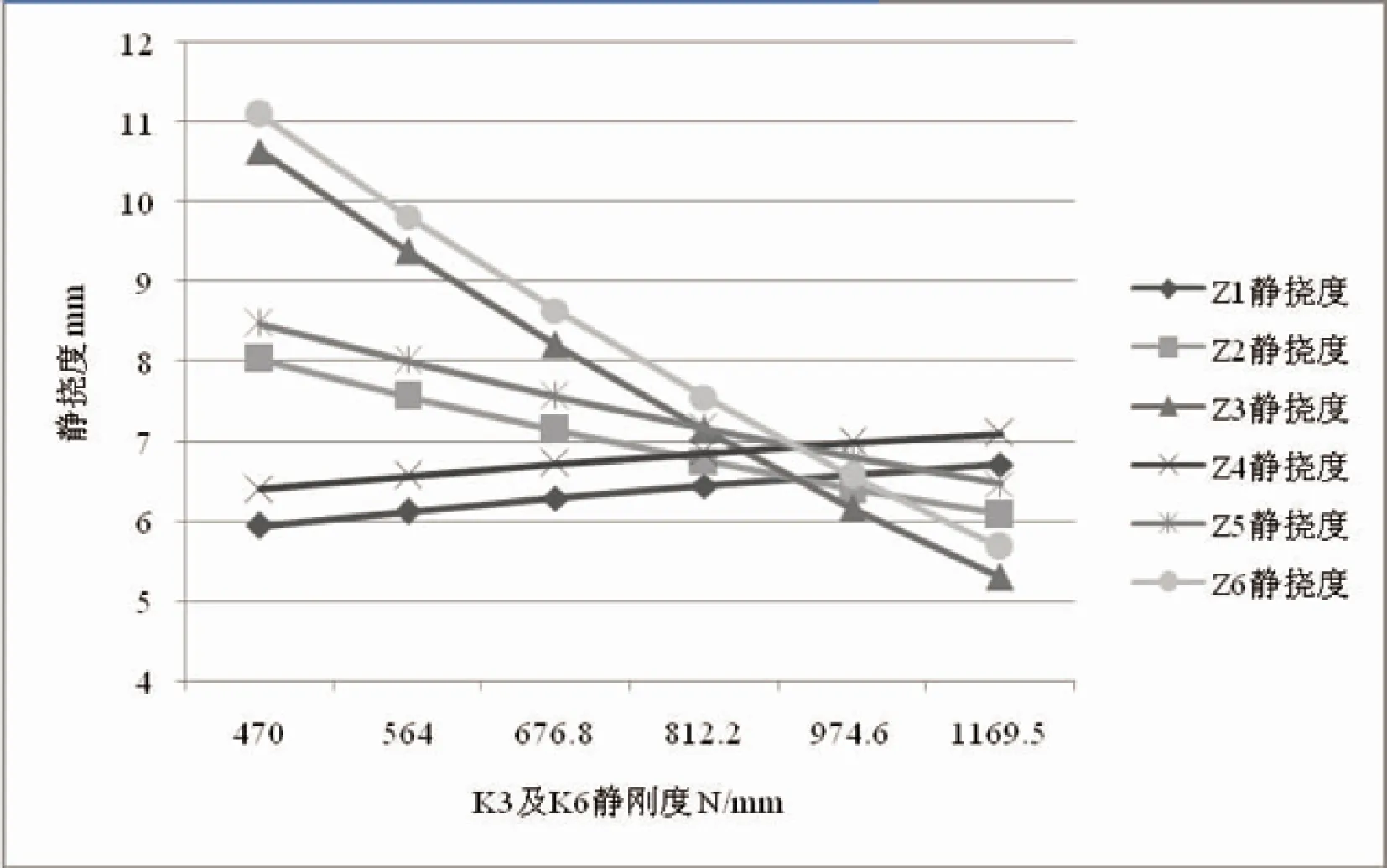
图5 静挠度随静刚度K3、K6变化图
从图5可以得到:当K1=K4=2 246 N/mm,K2=K5=1 502 N/mm时,
(1)2号、5号、3号及6号隔振器静挠度随着K3、K6刚度的增大而减小,1号及4号隔振器静挠度随着K3、K6刚度的增大而增大;
(2)在此刚度范围内,当K3=K6=974.6 N/mm时,存在满足6个隔振器的静挠度均在6~7 mm范围内的设计目标;
(3)根据表5工况22及工况24中Z1静挠度及K3刚度得到2点(812.2,6.44)及(1 169.5,6.71),根据2点直线公式得到直线方程(15):
Z1=0.000 8×K3+5.826 2
(15)
同理得到其余直线方程(16):
(16)
当K3、K6∈(918~1 020) N/mm时,Z1~Z6∈(6~7) mm;当K3、K6∈(832~1 033) N/mm时,Z1~Z6挠度差均在1 mm范围内。
具体结果见表7。
2.3各个隔振器满足行程指标6~7 mm条件下静刚度设计
变压器在自身质量下各个隔振器垂向静挠度最佳值均应在6~7 mm,对给定各个工况进行删选,得到各个隔振器静挠度均在6~7 mm的各个隔振器刚度值及对应的隔振器静挠度,见表8所示。

表6 给定隔振器刚度条件下计算各个隔振器的静挠度 Z/mm,K/(N·mm-1)

表7 Z1~Z6挠度差均在1 mm范围内的刚度范围 Z/mm,K/(N·mm-1)

表8 各个隔振器静挠度均在6~7 mm范围内的结果 Z/mm,K/(N·mm-1)
从表8可以看出:当K1=K4=2 695 N/mm,K2=K5=1 056 N/mm,K3=K6=1 169.5 N/mm时,6个隔振器静挠度分别为6.12,6.20,6.31,6.50,6.59,6.70 mm,均在6~7 mm范围内,同时各个隔振器静挠度差非常靠近,应当作为变压器刚度设计的参考选择。
3 结 论
通过上述分析可得到如下结论或方法:
(1)若牵引变压器隔振器6点满足共平面条件下的几何约束协调方程,则隔振器静挠度应当满足Z4-Z1=Z5-Z2=Z6-Z3的关系。
(2)得到了给定隔振器静挠度条件下设计隔振器刚度、给定隔振器刚度条件下计算各个隔振器的静挠度的方法。
(3)得出了各个工况下静挠度差均在1 mm范围内对应的各个静刚度及静挠度值。
(4)得出了各个工况下静挠度均在6~7 mm范围内对应的各个静刚度及静挠度值。当K1=K4=2 695 N/mm,K2=K5=1 056 N/mm,K3=K6=1 169.5 N/mm时,6个隔振器静挠度分别为6.12,6.20,6.31,6.50,6.59,6.70 mm,均在6~7 mm范围内,同时各个隔振器静挠度差非常靠近,应当作为变压器刚度设计的参考选择。
(5)若需要考虑隔振器每个吊挂点处车体挠度值的不同,还需考虑变压器具体安装于车体下方的位置即车体的变形,有待于进一步研究。
[1]Y.Suzuki,K.Akutsu,E.Maebashi,M.Sasakura and T.Tomioka.Method for flexural vibration damping of rolling stock carbody[J].QR. Of RTRI,1997,(38):123-128.
[2]Lu S,Hillmansen S,Roberts C.Power management strategy study for a multiple unit train[C].IET Conference on Railway Traction Systems(RTS 2010),2010.
[3]ZHANG Hongliang,ZHAO Peng,YANG hao.Distribution of electric multiple unit maintenance base of high-speed railway[C].SOLI 2008,959-964.
[4]吴会超,邬平波,曾京,等.车下设备对车体振动的影响[J].交通运输工程,2012,12(5):51-56.
[5]吴会超, 邬平波,吴娜,等.车下设备悬挂参数与车体结构之间匹配关系研究[J].振动与冲击,2013,32(3):125-128.
[6]石怀龙,邬平波,罗仁.高速动车组弹性车体和设备耦合振动特性[J].西南交通大学学报,2014,49(4):693-699.
[7]石怀龙,罗仁,邬平波.基于动力吸振原理的动车组车下设备悬挂参数设[J].机械工程学报,2014,50(14):155-160.
[8]宫岛,周劲松,孙文静,等.下吊设备对高速列车弹性车体垂向运行平稳性影响[J].中国工程机械学报,2011,9(4):404-409.
[9]Sun Wenjing,Gong Dao,Zhou Jinsong. Influences of Suspended Equipment under Car Body on Highspeed Train Ride Quality [J].Procedia Engineering,2012 (16) :812-817.
[10]陈亮,康洪军,张立民.牵引变压器连接刚度对车体与设备振动影响分析[J].铁道车辆,2012,50(8):4-5,29.
Design Research of Suspension System Static Stiffness for Traction Transformer
ZHANGYuanliang
(Automotive and Information Engineering, Sichuan Urban Vocational College, Chengdu 610110 Sichuan, China)
Aiming at the stiffness design problem of rubber isolator between the carbody and the vehicle suspension devices of traction transformer, the force and moment balance equations of the traction transformer have been obtained based on a simplified force model of the transformer. Designing isolator stiffness method under the given condition of static deflection and calculating each isolator static deflection method under the given condition of isolator stiffness have been obtained according to geometry compatibility equations of 6 points coplanar conditions. Static stiffness of an EMU traction transformer has been designed as an example. Isolator stiffness conditions are given and each isolator static deflection has been obtained. Each isolator static deflection difference is considered, to obtain the static stiffness of each isolator whose static deflection difference is in the range of 1mm. Considering the principle of each isolator static deflection in the range of 6~7 mm, static stiffness and the corresponding static deflection of each isolator are obtained.
traction transformer; stiffness design; static stiffness; static deflection
1008-7842 (2016) 02-0001-07
8—)男,工程师(
2015-09-14)
U260.331+7
Adoi:10.3969/j.issn.1008-7842.2016.02.01
*国家科技支撑计划项目(2009BAG12A04-(03))

