自导向转向架曲线运行轴间抗剪系统受力研究*

梁骏宇， 周张义， 杨　欣， 黄运华

(西南交通大学　机械工程学院， 四川成都 610031)



自导向转向架曲线运行轴间抗剪系统受力研究*

梁骏宇， 周张义， 杨欣， 黄运华

(西南交通大学机械工程学院， 四川成都 610031)

为显著提升曲线通过性能，自导向转向架采用低轴箱纵向定位刚度和大锥度踏面轮对成为必然，从而需要额外附加轴间抗剪系统以确保足够的直线蛇行稳定性。首先，基于线性稳态解析并以最佳曲线通过为目标，论述了Scheffel提出的轴箱纵向定位刚度匹配设计原理；其次，进行非线性动态曲线通过数值仿真，验证了参数匹配条件下轴间抗剪系统处于不承载的理想工作状态；最后，组合不同轴箱纵向定位刚度和轴间抗剪系统剪切刚度参数取值，仿真分析了参数不匹配条件下轴间抗剪系统的受力变化规律，提出自导向转向架要实现最佳曲线通过，则必须采用匹配设计的轴箱纵向定位刚度，此时轴间抗剪系统仅在直线运行时承受较大载荷；若转向架其他运行性能要求采用更大的轴箱纵向定位刚度，则为确保曲线通过较大程度接近最佳性能，实际应用的参数应取匹配值的2～4倍为宜，轴间抗剪系统的剪切刚度尽量取低值，此时其在曲线运行时承受较小载荷。

自导向转向架； 曲线通过； 轴间抗剪系统； 受力分析； 剪切刚度； 轴箱纵向定位刚度

车辆通过曲线时，轮对不出现轮缘贴靠钢轨，并最大程度沿径向纯滚线运动，从而显著降低轮轨磨耗，是自导向转向架的设计目标。为此，采用大锥度踏面轮对和低轴箱纵向定位刚度成为必然。由于这将同时导致直线蛇行稳定性大幅降低，因此自导向转向架需额外设置轴间抗剪系统。其根本作用是提供转向架主要的剪切刚度，确保足够的直线蛇行稳定性，同时不影响柔软轴箱纵向定位形成的转向架低弯曲刚度，确保高曲线通过性能。图1为3种典型轴间抗剪系统示意图。

理论上，根据蠕滑力导向机理，轴间抗剪系统并不能被认为是一种导向装置。转向架自导向完全是依靠具有足够车轮踏面锥度的低摇头约束轮对，在曲线上依靠轮轨蠕滑力自动调整至径向纯滚位置实现的。轴间抗剪系统应根据不妨碍轮对曲线自导向能力原则设计，其在转向架中仅仅起稳定直线蛇行运动的作用。基于此，轴间抗剪挂系统在转向架曲线运行中并不承受很大

载荷，理想工作模式是处于不承载的自由释放状态，从而其剪切刚度不影响轮对自导向能力，此时转向架可实现最佳曲线通过。

以往研究中，以最佳曲线通过为目标，就自导向转向架关键参数匹配设计研究基本来自于Scheffel[1-4]，核心为轮对轴箱纵向定位刚度与其重力刚度间的参数匹配。而更多偏向工程化的应用研究[5-7]，通常仅强调相对于常规转向架，自导向转向架应采用较低轴箱纵向定位刚度的必要性，但基本未涉及实现最佳曲线通过所需相关参数间的潜在匹配问题。实际应用中的参数取值设计仍基于常规折中法，即在满足车辆各项运行性能指标基础上，选取较低轴箱纵向定位刚度。

可见，上述两种不同的参数设计方法，势必导致自导向转向架曲线运行时轴间抗剪系统处于不同的受力状态。由于前者采用匹配设计的参数，着重强调实现最佳曲线通过，因此其轴间抗剪系统通常受力很小，接近处于不妨碍轮对曲线自导向的理想工作状态；而后者并不进行严格的参数匹配，着重折中考虑各类运行性能，无法达到最佳曲线通过，故其轴间抗剪系统通常受力不小，轮对自导向能力将受到一定影响。

考虑到轴间抗剪系统受力状态，不仅影响自导向转向架曲线通过性能，而且直接关系其结构自身强度可靠性设计。鉴于此，针对Scheffel提出的参数匹配设计原理进行必要论述基础上，着重应用多体动力学数值仿真技术，系统分析关键悬挂参数不同组合条件下，自导向转向架曲线运行时轴间抗剪系统的受力状态及变化规律，为工程应用中更为合理的参数设计提供理论依据。

1　轴箱纵向定位刚度匹配设计

在足够轮轨间隙前提下，车轮踏面具有锥度的自由轮对具备沿曲线径向纯滚动的能力，即轮对轴线在径向线上和轮对中心在纯滚线上。当轮对偏离该稳态位置时，借助轮轨间相应产生的蠕滑力，轮对将围绕径向纯滚线持续进行回调运动，完成曲线导向运行。

可见，轮对需要满足零摇头约束和纯滚线位于轮轨间隙之内两个条件，才能达到理想曲线通过。考虑实际有限的轮轨间隙，如我国LM型踏面轮对与60 kg/m钢轨匹配时的轮轨间隙约为9 mm，必须采用大锥度踏面轮对，方能使自导向转向架通过小半径曲线时不出现轮缘贴靠钢轨。

对于大锥度踏面轮对，由于其发生横移运动后存在显著的重力刚度Kws，相应产生的横向重力复原力Kws对轮对受力平衡产生较大影响，因此在轮对曲线通过受力分析中不能忽略。在该情形下，对于两轴间弯曲刚度为零的轮对，因横向受力不平衡其曲线通过的理想稳态位置将无法达到径向线，如图2(a)所示。前后轮对必须同时逆时针旋转一定摇头角而产生轮轨横向蠕滑力，以平衡非零重力刚度引起的横向重力复原力，达到实际稳态平衡位置，如图2(b)所示。此时轮对仍可达到纯滚线位置，即轮轨间仅有横向蠕滑而无纵向蠕滑。图2中，r0为车轮名义滚动圆半径，λ为车轮踏面等效锥度，2a为转向架轴距，2l为同一轮对轮轨接触点横向跨距，2θ为轴间径向夹角，y0为轮对纯滚横移量，R为线路曲线半径，Kx为轴箱纵向定位刚度。

进一步，如果轴间弯曲刚度不为零，即存在一定轴箱纵向定位刚度，则由于定位弹簧变形承载而影响轮对受力平衡，导致理想纯滚线也无法达到。如图2(c)所示，为使得轮对在横向、纵向及回转方向均达到受力平衡，一方面前后轮对需要相对纯滚线分别向外和向内横移，以便产生作用方向相反的纵向蠕滑力矩来平衡定位弹簧复原力矩，达到轮对在纵向和回转方向的受力平衡；另一方面，前后轮对还需分别逆时针和顺时针反相摇头，以便使前后轮对横向蠕滑力发生增减，适应因轮对相对纯滚线横移而产生的横向重力复原力增减，达到轮对在横向的受力平衡。

上述分析表明，当采用大锥度踏面轮对后，与轴箱纵向定位刚度一样，重力刚度也成为影响曲线通过不可忽略的负面因素，且二者间存在耦合作用影响。虽然零弯曲刚度是保证转向架理想曲线通过的前提，但其也将导致表征蛇行运动失稳的临界速度为零，实际中不可能采用。实际上，对于采用大锥度踏面轮对的自导向转向架，一定的轴箱纵向定位刚度还将有利于降低重力刚度对曲线通过的不利影响。当二者参数间达到特定匹配关系时，不利影响将降至最低，轴间抗剪系统可处于不承载的自由释放状态，达到其剪切刚度仅决定直线蛇行稳定性，而不影响曲线通过性能的理想工作模式。

对于采用大锥度踏面轮对、轴间存在一定弯曲刚度且附加轴间抗剪系统的二轴自导向转向架，同样由于受力不平衡轮对无法达到理想曲线通过的径向纯滚位置，如图3(a)所示。类似图2，经过整体回转和轮对间反相摇头运动的叠加，转向架可达到实际的最终受力平衡稳态位置。

图2　大锥度踏面轮对曲线稳态位置分析

图3　自导向转向架轮对曲线稳态位置分析

首先，转向架系统可整体绕其垂向中心轴逆时针回转角φ，如图3(b)所示(图中f11和f22分别为轮轨纵向和横向蠕滑系数)，前后轮对由此产生平衡横向重力复原力的横向蠕滑力，即：

(1)

其中：Kws为重力刚度。

因此，满足上式所需的整体回转角为：

(2)

相应地，该整体回转角引起的前后轮对相对纯滚线向外和向内的横移量为ΔY=aφ，从而导致其各自横向重力复原力的增减量为：

(3)

可见，此时每个轮对的横向蠕滑力和横向重力复原力不平衡。对于前轮对，横向蠕滑力小于横向重力复原力，而后轮对则刚好相反，每个轮对的横向不平衡力即为ΔF。要使其各自达到最终的横向受力平衡，则轴间径向夹角2θ需减小2φ，即前后轮对分别逆时针和顺时针产生反相摇头角φ，如图3(c)所示，使各自轮轨横向蠕滑力分别增减达到2f22φ=ΔF。因此，轮对横向平衡所需的摇头角φ为：

(4)

(5)

将式(2)和式(4)代入式(5)并整理可得：

(6)

上述分析表明，若轮对轴箱纵向定位刚度与其重力刚度达到式(6)所表达的匹配关系，则通过该纵向定位弹簧的耦合作用，前后轮对将在纵向及回转方向也达到受力平衡。此外还可得知，由于整体回转角φ和反相摇头角φ两种调节运动，均不会引起轴间抗剪系统承受载荷作用，因此轮对在水平方向内的力及力矩平衡与其剪切刚度取值无关。

以上即是Scheffel基于线性转向架系统的稳态曲线通过分析，提出的自导向转向架轴箱纵向定位刚度的匹配设计基本原理。若再假设轮轨纵向和横向蠕滑系数也相等，并忽略角φ(小半径曲线上该值通常很小)的影响，则式(6)可进一步简化为：

(7)

可见，就确定的线路和转向架总体几何参数，轮对轴箱纵向定位刚度与其重力刚度间存在单调线性关系。基于该参数设计方程，自导向转向架可实现略微偏离理想径向纯滚位置的最佳曲线通过。

2　参数匹配下轴间抗剪系统受力验证

如上论述，当轮对轴箱纵向定位刚度与其重力刚度达到匹配设计时，自导向转向架最佳曲线通过得以实现，轴间抗剪系统将处于不承载的自由释放状态，其剪切刚度对曲线通过性能无影响。考虑到该结论是在诸多前提假设下进行线性稳态解析得到的，如轮轨接触、蠕滑和弹性元件均呈线性特性，各向蠕滑系数相等及未考虑自旋蠕滑等。因此有必要在考虑各种实际因素条件下，对轴间抗剪系统的受力进行验证。

应用SIMPACK多体动力学仿真软件，考虑轮轨接触几何非线性、各向蠕滑非线性、自旋蠕滑等实际因素，基于我国LM型踏面轮对与60 kg/m钢轨匹配，建立了准轨25 t轴重3大件自导向转向架的动态曲线通过仿真模型。其中，轴间抗剪系统采用图1(a)所示方案，每个副构架首先将同一轮对左右轴箱相连，然后通过两交叉杆进行铰接，两交叉杆承受的轴向拉压载荷即可体现整个轴间抗剪系统的受力状态。

首先，通过变参数分析，分别仿真确定转向架在曲线半径线路300～600 m上，以均衡速度运行达到最佳曲线通过所需的轴箱纵向定位刚度值。根据线性解析推导,最佳曲线通过的实现标准为轴间抗剪系统处于基本不承载的自由释放状态，即交叉杆载荷最小，仿真中取其目标载荷值小于0.1 kN。表1所列为仿真和按式(7)解析确定的轴箱纵向定位刚度匹配值结果对比。可见，二者存在一定差异，仿真结果要小于解析结果，即要达到最佳曲线通过实际中需要更小的轴箱纵向定位刚度。若解析推导中尽可能减少简化和假设，则解析结果将接近仿真结果。

表1　轴箱纵向定位刚度解析和仿真匹配结果对比

从表1还可看出，一方面自导向转向架所需最优轴箱纵向定位刚度较常规转向架要小的多，通常至少要小一个数量级，如南非Scheffel转向架采用的定位刚度最小达0.3 MN/m；另一方面，由于随线路曲线半径减小，轮对纯滚所需横移量增大，重力刚度也相应增大，从而匹配确定的定位刚度呈增大趋势。

图4所示为转向架以均衡速度运行至圆曲线上，轮对稳态横移和冲角(相对于径向线的摇头角)仿真与解析结果对比，图中同时给出了纯滚横移量和轴箱纵向定位刚度很大的刚性转向架轮对冲角(a/R)。可见，一方面仿真与解析结果不仅差异很小，而且分布规律也相同，即前后轮对相对纯滚线分别向外和向内横移，相对径向线均摇头呈欠导向状态，且前轮对冲角略大于后轮对；另一方面，通过与纯滚横移量和刚性转向架轮对冲角对比可知，前后轮对处于略微偏离理想径向纯滚线的位置，验证了通过匹配设计轴箱纵向定位刚度，可使自导向转向架达到最佳曲线通过。

图4　轮对稳态横移和冲角的解析与仿真结果对比

表2列出了轴间抗剪系统剪切刚度Ks取不同值，转向架通过300 m和600 m半径曲线时，轮对稳态横移和冲角仿真结果对比。可见，当采用匹配设计的轴箱纵向定位刚度后，Ks取值将不影响轮对的曲线通过稳态运动位置。图5所示为转向架通过300 m半径曲线时，Ks分别取3，6，12，24 MN/m，交叉杆载荷时间历程仿真结果对比。可见，在圆曲线上交叉杆稳态载荷几乎为零，且与Ks无关，轴间抗剪系统处于基本不承载的理想工作状态；在缓和曲线上，由于线路曲率和超高不断变化，导致参数间匹配关系暂时丧失，从而交叉杆将瞬态承载，且其载荷随Ks增大而增大，与文后给出的参数不匹配条件下交叉杆载荷变化规律类似。其中，交叉杆1延长线指向前轮对外侧轴箱和后轮对内侧轴箱，交叉杆2与之相反。

表2　不同Ks下轮对稳态横移和冲角仿真结果对比

图5　不同Ks下交叉杆载荷仿真结果对比

图6所示为转向架以均衡速度通过300 m半径曲线时，有无轴间抗剪系统下轮对横移和冲角时间历程仿真结果对比。可见，两种情形下轮对在圆曲线上的稳态运动时间历程几乎一致，不受Ks影响；在缓和曲线上，同样由于参数匹配关系的暂时丧失，从而轴间抗剪系统的存在将导致轮对运动，尤其是摇头运动较无轴间抗剪系统转向架轮对发生变化，一定程度上说明轴间抗剪系统不仅影响导向装置，而且在参数不匹配条件下还将影响轮对的自导向能力。

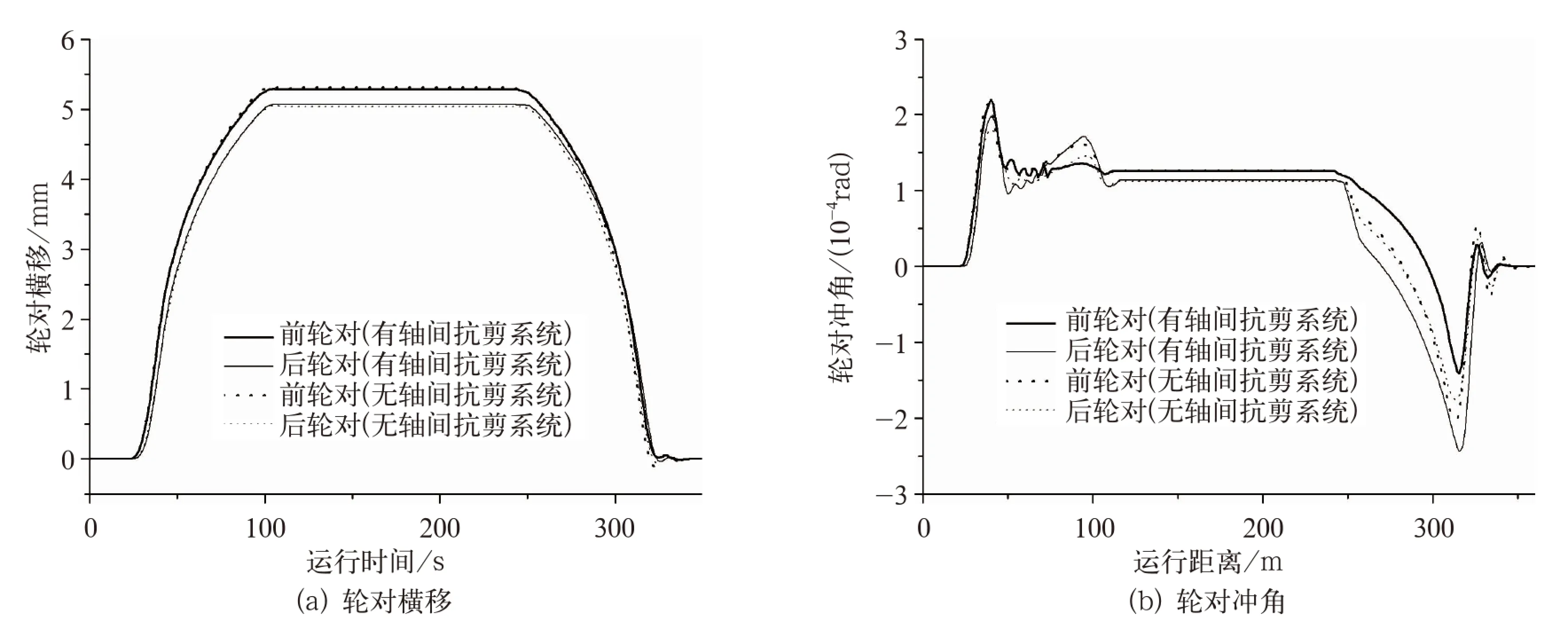
图6　有无轴间抗剪系统的轮对横移和冲角时间历程仿真结果对比

3　不同参数组合下轴间抗剪系统受力分析

根据表1所列仿真结果，若就最小曲线半径为300 m 的线路进行最佳曲线通过优化，则可以匹配得到我国25 t轴重自导向转向架轴箱纵向定位刚度约为0.5 MN/m。可见，该定位刚度较常规转向架要小得多。若对转向架要求较高直线蛇行稳定性或定位弹簧同时要传递很大的纵向载荷，则该参数取值较难在工程中应用，实际中选取更大的轴箱纵向定位刚度参数成为必然。在此情形下，决定最佳曲线通过的参数匹配关系在圆曲线上也将失去，轴间抗剪系统必然稳态承载，其剪切刚度不仅决定直线蛇行稳定性，而且影响曲线通过性能。

分别取Kx为1，1.5，2，3，5 MN/m，Ks为3，6，12，24 MN/m，对这些参数依次组合进行自导向转向架动态曲线进行仿真分析。图7所示为转向架通过300 m和600 m半径曲线时，交叉杆1稳态载荷仿真结果对比。交叉杆1和交叉杆2的稳态载荷大小几乎相等，但作用方向相反，二者分别承受轴向拉伸和压缩载荷，

图7　不同Kx和Ks参数组合下交叉杆1稳态载荷仿真结果对比

从图7及数据对比分析表明，Kx和Ks组合一定时，交叉杆稳态载荷将基本随转向架通过的曲线半径增大而减小；当Kx一定时，交叉杆稳态载荷将随Ks增大而增大；Ks一定时，交叉杆稳态载荷也将随Kx增大而增大。在缓和曲线上，交叉杆瞬态载荷在不同Kx和Ks组合下具有相同的变化规律，如图8所示转向架通过300 m半径曲线时，交叉杆载荷时间历程仿真结果对比。

相应地，图9和图10所示为转向架通过300 m半径曲线时，不同Kx和Ks组合下轮对横移及冲角时间历程仿真结果对比。针对结果的系统分析及对比表明，当Kx一定，随Ks增大前后轮对均将逐渐横向外移，前轮对稳态位置偏离纯滚线的程度大于后轮对。在Kx取值较小时，上述横向外移和偏离纯滚线程度均很小，如图9(a)所示。在Kx取值较大时，相应的横向外移和偏离纯滚线程度均很大，如图9(b)所示。可见，尽可能采用接近匹配值(0.5 MN/m)的低轴箱纵向定位刚度，不仅能有效降低轮对偏离纯滚线的程度，而且使其对轴

图8　不同Kx和Ks参数组合下交叉杆载荷时间历程仿真结果对比

图9　不同Kx和Ks参数组合下轮对横移时间历程仿真结果对比

图10　不同Kx和Ks参数组合下轮对冲角时间历程仿真结果对比

间抗剪系统剪切刚度不敏感。

当Ks一定且取值较小时，随Kx增大前后轮对将分别逐渐横向外移和内移，如图9(c)所示。当Ks一定且取值较大时，随Kx增大前后轮对均将逐渐横向外移，如图9(d)所示。两种情形下，前轮对稳态位置偏离纯滚线的程度均大于后轮对。

当Kx一定且取值较小时，随Ks增大前后轮对将反相摇头，前轮对始终呈欠导向且冲角逐渐增大，后轮对初始呈欠导向且冲角逐渐较小，随后呈过导向且冲角逐渐增大，如图10(a)所示，当Kx一定取值较大时，随Ks增大前后轮对也将反相摇头，前轮对稳态位置始终呈欠导向且冲角逐渐增大，后轮对稳态位置则始终呈过导向且冲角也逐渐增大，如图10(b)所示。两种情形下，前轮对稳态位置偏离径向线的程度均大于后轮对。此外同上所述，尽可能采用接近匹配值的低轴箱纵向定位刚度，不仅能有效降低轮对偏离径向线的程度，而且也可使因轴间抗剪系统剪切刚度增大而引起轮对冲角变化的程度最小。

当Ks一定时，轮对冲角随Kx增大而发生的变化也有同上基本类似的规律。

进一步对比上述交叉杆载荷与轮对运动位置的变化规律可知，自导向转向架曲线运行时，轴间抗剪系统的承载大小与轮对偏离最佳曲线通过运动位置的程度直接相关。轴间抗剪系统承载越大，则轮对偏离最佳曲线通过运动位置程度越大，从而轮轨间蠕滑也越大，使得轮对出现滑行的可能性也越大，最终导致转向架曲线通过性能恶化。因此，通过合理优化参数，尽可能降低轴间抗剪系统受力，不仅可使自导向转向架接近潜在的最佳曲线通过，而且利于轴间抗剪系统自身结构的强度可靠性设计和运用。

4　工程应用建议

综上分析，自导向转向架要实现最佳曲线通过，则必须采用匹配设计的轴箱纵向定位刚度，此时轴间抗剪系统在圆曲线上可实现不承载的理想工作状态，同时要确保其在缓和曲线上受力也较小，则应尽量采用低值剪切刚度参数。

当转向架其他运行性能要求采用较匹配值更大的轴箱纵向定位刚度时，为确保曲线通过较大程度接近最佳性能，同时使轴间抗剪系统承载较小，则轴箱纵向定位刚度及轴间抗剪系统剪切刚度两参数的取值均不宜过大，尤其是轴箱纵向定位刚度。

表3列出了转向架通过300 m半径曲线时，Kx分别取0.5,1,2,4 MN/m，Ks分别取3,6,12 MN/m，在两种参数各种组合条件下，转向架在圆曲线上各轮对的轮轨稳态蠕滑力仿真结果对比。

表3　不同Kx和Ks参数组合下轮轨稳态蠕滑力仿真结果对比　kN

对比表3数据可见，一方面除后轮对外侧车轮外，转向架其他车轮合成蠕滑力都将随Kx和Ks增大而增大，转向架总体曲线通过性能将降低；另一方面，Kx对轮轨蠕滑力的影响程度显著高于Ks。如当Ks为6 MN/m，Kx分别取匹配值(0.5 MN/m)的2倍(1 MN/m)、4倍(2 MN/m)和8倍(4 MN/m)时，前轮对外侧车轮的合成蠕滑力将分别增大9.3%、25.1%和84.6%。当Kx增至4 MN/m时，合成蠕滑力将超过36 kN，十分接近轮轨间最大静摩擦力(取轮轨摩擦系数为0.3)，很可能首先出现滑行而显著增大轮轨磨耗。

综上分析，为尽可能降低增大轴箱纵向定位刚度对曲线通过的不利影响程度，工程应用中其参数取值不宜超过匹配值的4倍，以2倍左右为最佳。在此条件下，采用低值轴间抗剪系统剪切刚度，将有利于进一步提高曲线通过性能。理论分析表明，对于我国25t轴重自导向转向架，1 MN/m的轴箱纵向定位刚度和5 MN/m的轴间抗剪系统剪切刚度参数组合取值，已可以完全满足车辆120 km/h的最高速度和其他运行性能指标要求，同时曲线通过仍能很大程度接近潜在的最佳性能。

5　结　论

(1) 论述了Scheffel提出的自导向转向架轮对轴箱纵向定位刚度的匹配设计原理。当其达到特定匹配值时转向架可实现最佳圆曲线通过，轴间抗剪系统将处于不承载的理想工作状态，其对轮对自导向能力的不利影响将得到有效控制；

(2) 基于非线性动态曲线通过数值仿真分析，验证了参数匹配条件下自导向转向架可实现最佳曲线通过，轴间抗剪系统的存在并不是作为导向装置而发挥导向作用，而应仅将其视为稳定转向架直线蛇行运动的轴间耦合装置；

(3) 仿真分析了参数不匹配条件下，轴间抗剪系统受力及轮对运动状态的变化规律。结果表明，轴间抗剪系统的承载大小与轮对偏离最佳曲线通过运动位置的程度直接相关。通过合理优化参数，尽可能降低轴间抗剪系统受力，不仅可使自导向转向架接近最佳曲线通过，而且利于轴间抗剪系统自身结构的强度可靠性设计和运用。

(4) 自导向转向架要实现圆曲线上的最佳曲线通过，则必须采用匹配设计的轴箱纵向定位刚度，同时要确保缓和曲线上的良好通过性能，轴间抗剪系统的剪切刚度也应尽量低；

(5) 若转向架其他运行性能要求采用更大的轴箱纵向定位刚度，则为确保曲线通过较大程度接近最佳性能，实际采用的参数应取匹配值的2～4倍为宜，轴间抗剪系统剪切刚度也应尽量取低值。

[1]H．Scheffel．The Hunting Stability and cCurving Ability of Railway Vehicles[J]．Rail International，1974，(2)：154-176．

[2]H．Scheffel，H M．Tournay．An Analysis of Steady State Deviations of Wheelsets from the Pure Rolling Position Caused by Curved Track and Bogie Inaccuracies[J]．Vehicle System Dynamics，1983，12(1-3)：14-18．

[3]H．Scheffel．南非铁路径向转向架的设计[J]．电力牵引快报，1995，(8-9)：8-13．

[4]H．Scheffel．Unconventional Bogie Designs-Their Practical Basis and Historical Background[J]．Vehicle System Dynamics，1995，24(6-7)：497-524．

[5]R Joly．常规转向架与径向转向架的比较[J]．国外铁道车辆，1989，26(3)：31-37．

[6]饭田浩平，等(日)．交叉杆式自导向转向架动力学性能分析[J]．国外铁道车辆，2007，44(6)：22-27．

[7]李亨利，李芾，傅茂海．货车径向转向架原理及其应用[J]．铁道车辆，2002，40(4)：25-26．

[8]李芾，傅茂海，黄运华．径向转向架机理及其动力学特性研究[J]．中国铁道科学，2002，23(10)：46-51．

Study on Stress of Inter-axel Shear System for Self-steering Bogie While Curving

LIANGJunyu，ZHOUZhangyi，YANGXin，HUANGYunhua

(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031 Sichuan, China)

In order to improve the curving ability remarkably, it is necessary to use low axel-box longitudinal stiffness and wheelsets with high tread conicity for self-steering bogie. Thus the inter-axel shear system is needed to ensure the enough hunting stability on straight lines. First of all, based on linear steady state analysis and aiming at the best curving, the principles of matching design of axel-box longitudinal stiffness proposed by Scheffel were discussed. Next, through the nonlinear dynamic curving numerical simulation, it is verified that the perfect working status that inter-axel shear system bear no loads while using matched parameters can be achieved. Finally, by combining the different parameter values of axel-box longitudinal stiffness and shear stiffness of inter-axel shear system, the loading variations of inter-axel shear system while using unmatched parameters were analyzed. According to the systemic analysis and comparison of results, the matching designed axel-box longitudinal stiffness must be used for self-steering bogie in order to obtain the best curving. At this case, the inter-axel shear system bears large loads only on straight lines. If the bigger axel-box longitudinal stiffness is needed to satisfy the other bogie running performance, it is recommended that its value applied in practice should be two to four times the matched value. The shear stiffness of inter-axel shear system should be low as soon as possible. In such way, the best curving performance can be reached to a large extent, and low forces will be loaded by inter-axel shear system.

self-steering bogie; curving; inter-axel shear system; stress analysis; shear stiffness; axle-box longitudinal stiffness

1008-7842 (2016) 02-0008-08

��)男，硕士研究生(

2015-11-09)

U260.331

Adoi:10.3969/j.issn.1008-7842.2016.02.02

*中央高校基本科研业务费专项基金资助(2682014CX030)