岩石断裂力学的扩展有限元法
周 博, 孙 博, 薛世峰
(中国石油大学储运与建筑工程学院,山东青岛 266580)
岩石断裂力学的扩展有限元法
周 博, 孙 博, 薛世峰
(中国石油大学储运与建筑工程学院,山东青岛 266580)
针对岩石材料的断裂力学问题阐述扩展有限元法的单元位移模式的选择、确定平面裂纹空间位置的水平集法和特殊单元的数值积分方法。介绍最大周向应力裂纹扩展判据和计算应力强度因子的相互作用积分法,进而建立岩石断裂力学的扩展有限元法。建立Ⅰ型裂纹和Ⅱ型裂纹的岩石断裂力学的扩展有限元计算模型,对I裂纹的应力强度因子和Ⅱ型裂纹的裂纹扩展路径进行扩展有限元法数值模拟计算。结果表明,建立的岩石断裂力学扩展有限元法可对岩石材料的断裂力学参数和裂纹扩展路径进行数值模拟分析,验证了数值计算结果的合理性,能有效地描述岩石断裂力学特性。
扩展有限元法; 水平集法; 应力强度因子; 相互作用积分法; 裂纹扩展判据; 裂纹扩展路径
石油开采、城市地铁、穿山隧道、水力水电等工程项目的建设都不可避免地涉及岩石区域。岩石的变形及破坏规律等力学性质对工程勘察、建设施工及运行安全性和可靠性等方面有重要影响。岩石破坏过程是其内部裂纹的萌生、扩展、直至贯通的结果。研究含裂纹岩石材料的力学性质,计算其断裂力学参数、预测其裂纹扩展规律,具有工程实际意义。解析方法只能解决少数简单的断裂力学问题,在实际应用中数值方法是研究断裂力学问题常用的重要而有效途径。有限元法[1]通过在裂纹尖端设置奇异单元,较好地描述了裂纹尖端位移、应变等物理场的奇异性,但是在模拟裂纹扩展时须重新划分网格,这极大地降低了计算效率。基于有限元法的黏聚力模型通过设置界面单元[2],可有效地实现对裂纹扩展的模拟,但需要预先得到裂纹的扩展路径,不适合模拟复杂裂纹的扩展问题。边界元法[3]能有效地处理裂纹等奇异性问题,且比有限元法精确和高效,但对非线性问题缺少高效计算方案,这限制了其应用范围。无网格法[4-6]的近似函数不依赖于网格,减少了因网格畸变带来的困难,可以高精度地模拟高速碰撞、动态裂纹扩展等问题,但无网格法对非线性问题的模拟,仍有待进一步开发。以Belytschko为代表的研究组[7-9],在有限元法的框架内建立了扩展有限元法(XFEM),很好地解决了由于材料或几何等因素引起的不连续问题,特别适合于处理断裂力学问题,近年来在众多领域的不连续问题的求解中不断得到成功应用[10-15]。笔者针对岩石材料的断裂力学问题,阐述XFEM的单元位移模式的选择、描述和追踪裂纹空间位置的水平集法及特殊单元的数值积分方法建立岩石平面裂纹问题的XFEM计算模型。利用MATLAB编写计算岩石断裂力学特性的XFEM程序,计算Ⅰ型裂纹的应力强度因子,模拟Ⅱ型裂纹的裂纹扩展路径。
1 XFEM基本原理
1.1 单元位移模式
XFEM的核心思想是在传统有限元法的单元移位模式中引入扩充项,以更精确地反映不连续性对单元移位及其他单元变量的影响。在XFEM中单元位移模式表示为
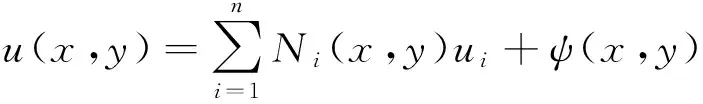
(1)
式中,x、y为空间坐标;u为单元位移分量;Ni为单元形函数;ui为单元结点位移分量;n为单元结点总数;ψ为反映不连续性的扩充项。
基于单位分解的思想和便于程序设计的考虑,扩充项ψ可表示为
(2)
式中,φj(x,y)为反映不连续性的增强函数;qj为结点位移分量ui的附加自由度;m为附加自由度的总数。
不同类型的不连续问题只须选取不同的增强函数φj(x,y)即可,其他处理过程完全相同,可见XFEM继承了传统有限元法的格式统一和便于编程的优点。
对于平面裂纹问题有两种特殊单元,一种是如图1所示的裂纹贯穿单元,另一种是如图2所示的包含裂纹尖端单元。对于如图1所示的裂纹贯穿单元,式(2)中的m等于1,增强函数取为
(3)
对于如图2所示的包含裂纹尖端单元,式(2)中的m等于4,增强函数取为
[φj(x,y)|j=1,2,3,4]=
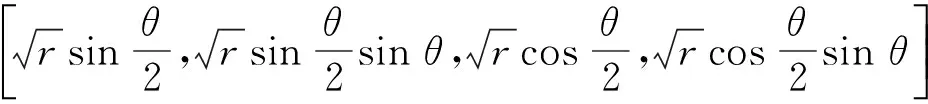
(4)
式中,r和θ为图2所示的裂纹尖端局部极坐标。
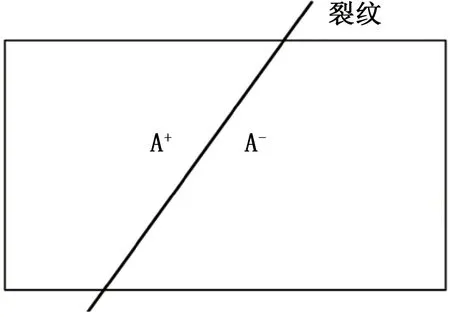
图1 裂纹贯穿的单元Fig.1 Element penetrated by crack
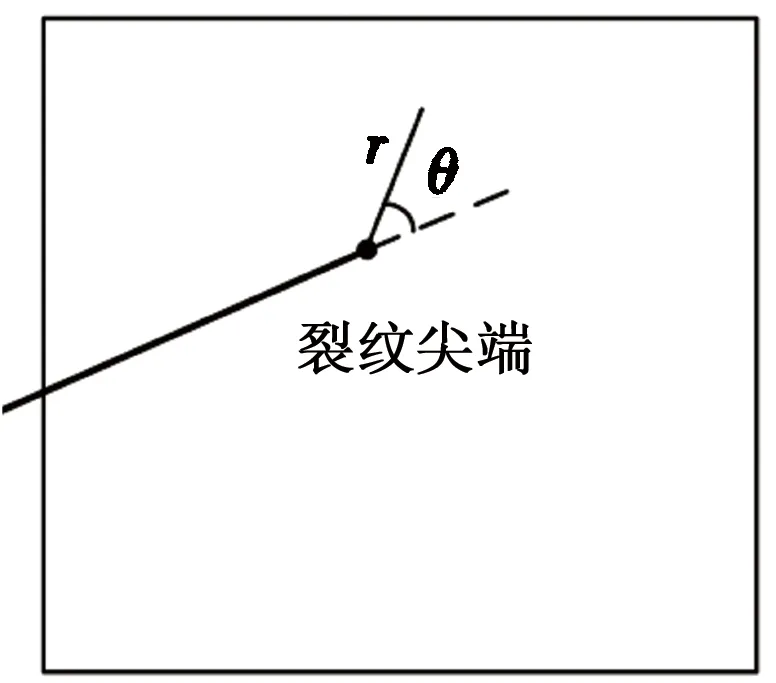
图2 包含裂纹尖端的单元Fig.2 Element containing crack tip
1.2 水平集法
和传统有限元法不同的是,在XFEM中网格的划分和间断面位置相互独立,间断面可以穿过单元。在XFEM中须对间断面进行几何描述,以方便识别单元和结点的类型。水平集法[16]是确定和追踪裂纹界面移动的数值方法,该方法用比裂纹界面维数高一维的水平集函数描述裂纹界面,裂纹界面的演化过程可表示为零水平集函数的变化过程。利用水平集法追踪界面演化的主要优点是,在描述界面运动时有限元网格不变,不必重新划分有限元网格就可以追踪界面运动。
常用的水平集函数是符号距离函数。对于图3所示的平面裂纹水平集函数,可用符号距离函数表示为
f[(x,y),t]=±min‖(x,y)-(x,y)Γ‖t,
(5)
g[(x,y),t]=±min‖(x,y)-(x,y)Γ′‖t.
(6)
式中,(x,y)为平面内任意一点的坐标;(x,y)Γ为裂纹上任意一点的坐标;(x,y)Γ′为过裂纹尖端虚线上任意一点的坐标;t为时间;f[(x,y),t]在裂纹上部取正号、在裂纹下部取负号;g[(x,y),t]在虚线左侧取正号、在虚线右侧取负号。
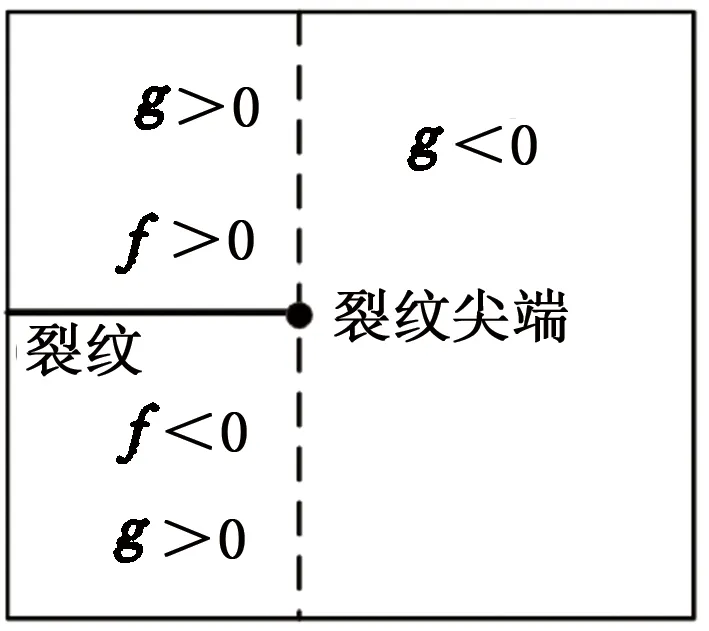
图3 描述平面裂纹的水平集函数Fig.3 Level set functions describing plane crack
1.3 特殊单元积分
在XFEM中为了反映间断面引起的不连续性,在包含间断面的特殊单元中引入描述不连续性的增强函数,致使这些单元的位移模式不再是光滑多项式函数,若对这些特殊单元仍采用传统有限元的高斯积分方案,将会引起较大的积分误差。
在XFEM的实际计算中,对这些特殊单元通常采用两种积分方法。第一种方法是采用子域积分法[10],即沿着间断面将单元分成若干个小区域,在每个小区域按传统有限元法的高斯积分方案积分,然后将所有小区域内的积分相加得到整个单元的积分。第二种积分方法[16]是在这些特殊单元内普遍加密高斯积分点,如对图4中裂纹贯穿单元和包含裂纹尖端单元均采用64个高斯积分点。第二种方法比第一种方法在程序设计中容易实现,因此本文采用第二种积分方法。
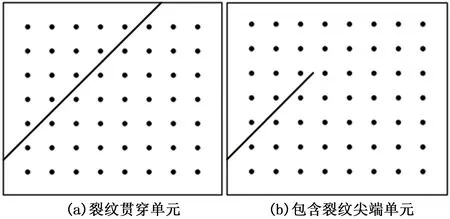
图4 特殊单元的积分方法Fig.4 Integral method for special elements
2 岩石断裂力学
岩石属于典型的脆性材料,可以用线弹性断裂力学理论描述其断裂力学特性。和XFEM密切相关的岩石断裂力学特性包括裂纹尖端位移分量求解、裂纹扩展的条件及应力强度因子计算等。
2.1 裂纹尖端位移场
根据线弹性断裂力学,含Ⅰ-Ⅱ复合型裂纹的无限大板在裂纹尖端附近的水平位移分量ux和竖直位移分量uy分别描述为
(7)
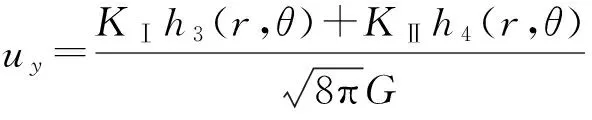
(8)
其中
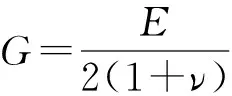
式中,KⅠ和KⅡ分别为Ⅰ型裂纹和Ⅱ型裂纹的应力强度因子;G为剪切弹性模量;E和ν分别为弹性模量和泊松比。
在式(7)中的h1(r,θ)和h2(r,θ)分别描述为
(9)
式中,r和θ为裂纹尖端局部极坐标。
在式(8)中的h3(r,θ)和h4(r,θ)分别描述为
(10)
在式(9)中的κ是一个与泊松比有关的系数,对于平面应力问题和平面应变问题的取值情况为

(11)
对比式(4)和式(9)可以发现,包含裂纹尖端单元的4个增强函数是线弹性断裂力学裂纹尖端位移场解析解中的4个函数项。可见含裂纹尖端单元的4个增强函数反映了裂纹尖端位移场的解析特性,可以有效地描述裂纹尖端引起的不连续性。
2.2 最大周向应力理论
对于Ⅰ-Ⅱ型复合平面裂纹,裂纹尖端局部极坐标系下的环向拉应力分量可描述为
(12)
其中
根据最大周向应力理论,裂纹的扩展方向和扩展条件为:裂纹扩展方向与最大周向拉应力方向垂直,即Kθ最大值的方向;当Kθ最大值达到极值时裂纹开始扩展。
将Kθ带入极大值条件
(13)
得到平面复合裂纹的扩展方向角θ0的计算式为
(14)
平面复合裂纹的扩展准则为
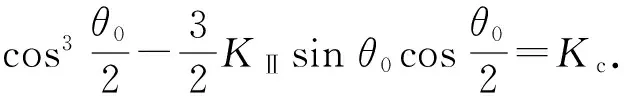
(15)
式中,Kc为材料断裂韧性,可通过实验测定。
2.3 相互作用积分法
计算应力强度因子的常用数值方法包括:结点位移外推法、单元应力外推法、相互作用积分法等。相互作用积分法具有很高的数值精度,在程序设计中容易实现,因此采用相互作用积分法计算应力强度因子。
相互作用积分是一个图5所示的在包含裂纹尖端的回路Γ上的能量积分,为了便于数值计算可将回路积分转换为图5所示的积分区域为A的面积分[17],即
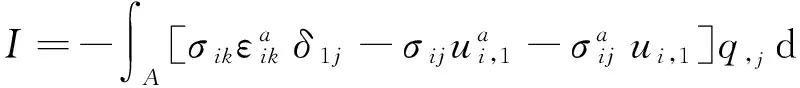
(16)
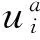
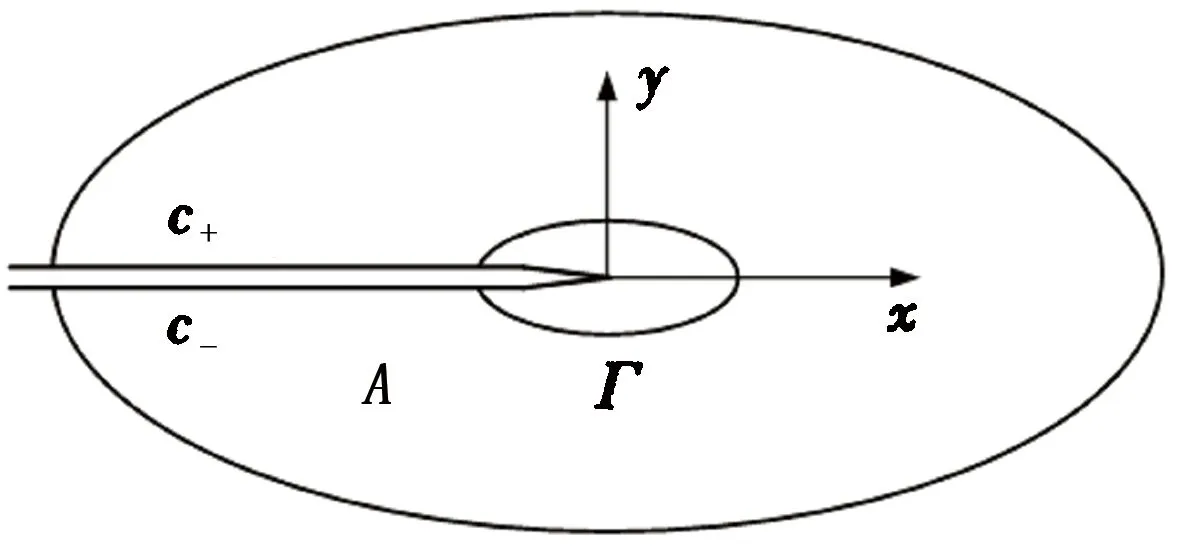
图5 相互作用积分法的积分区域Fig.5 Integral region for interaction integration method
应力强度因子K与相互作用积分I间的关系为
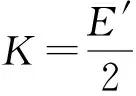
(17)
E′对于平面应力问题和平面应变问题的取值情况为
(18)
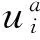
3 数值算例
基于XFEM基本原理和岩石断裂力学,利用MATLAB编写描述岩石断裂力学特性的XFEM计算程序,对Ⅰ型裂纹的应力强度因子和Ⅱ型裂纹的裂纹扩展路径进行数值模拟计算。
3.1 应力强度因子计算
如图6所示边长W=2 m的正方形,左部居中有一个长度为a的水平裂纹,作用在上下两边的拉伸载荷σ为1.0×106Pa,材料的弹性模量E为15×109Pa、泊松比ν为0.25、断裂韧性Kc为8.22×106N/m1.5。
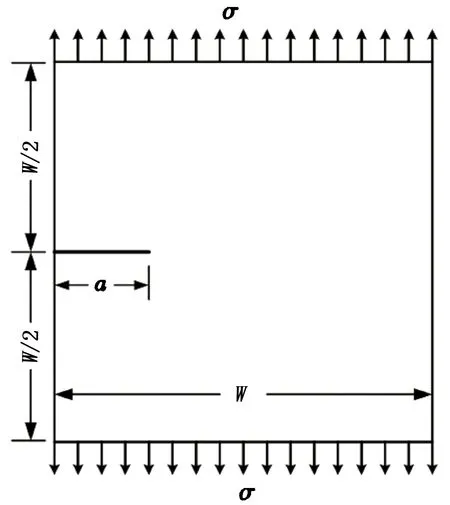
图6 含Ⅰ型裂纹的几何实体Fig.6 Geometrical model with crack of mode Ⅰ
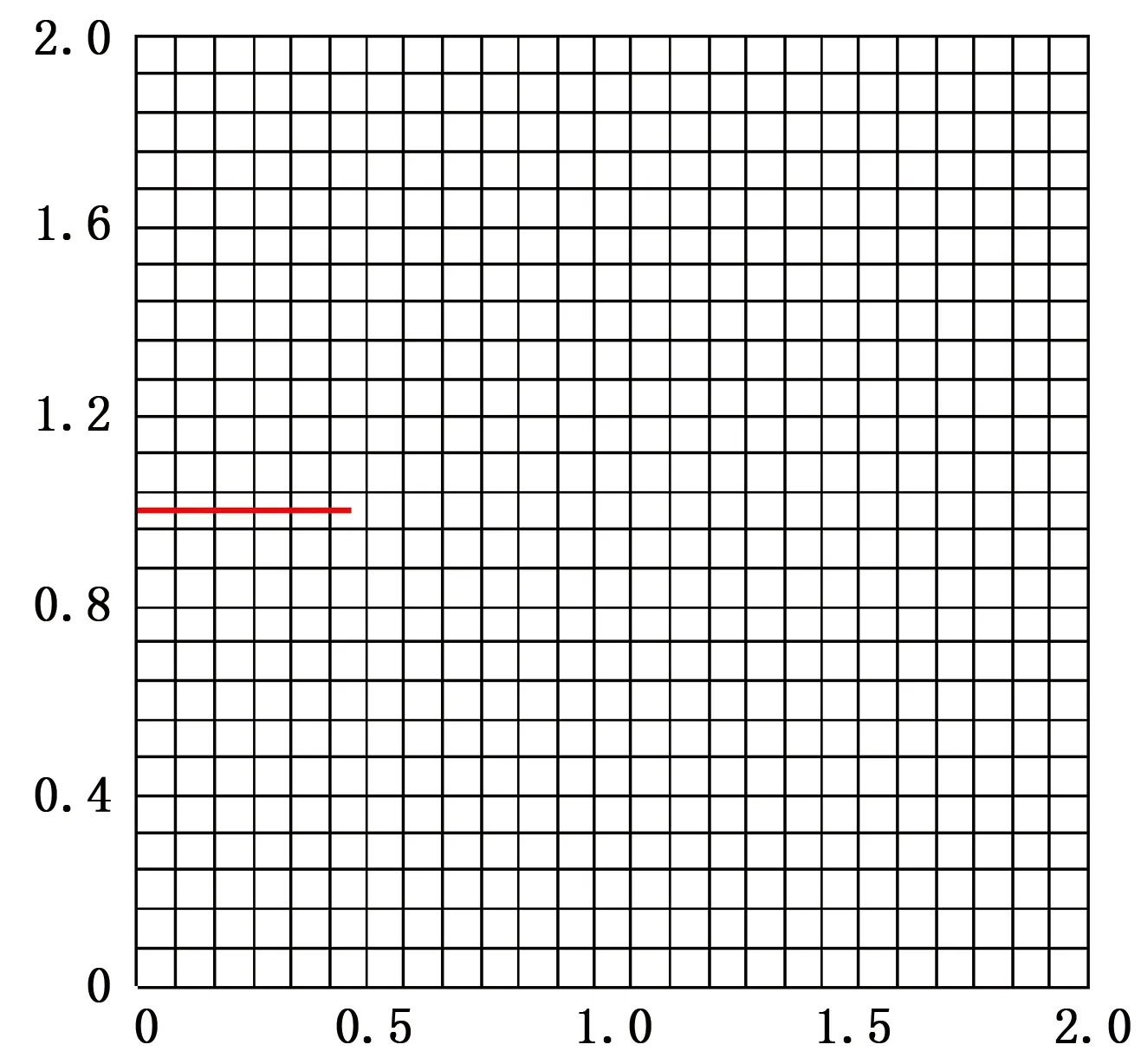
图7 XFEM计算模型Fig.7 Numerical calculating model based on XFEM
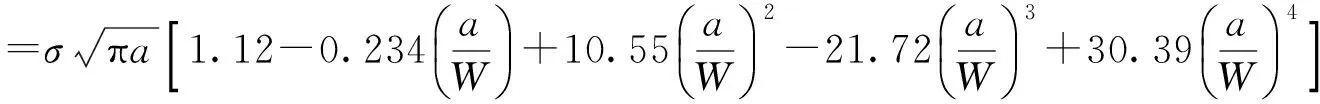
(19)
计算得到。
从表1的数值计算结果可以看出,XFEM计算应力强度因子有较高的数值计算精度。
表1 应力强度因子KⅠ的计算结果
Table1CalculatingresultsofstressintensityfactorKⅠ
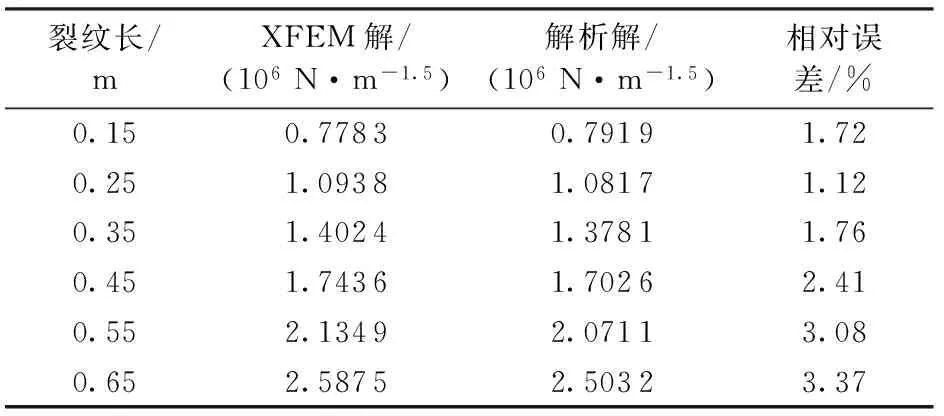
裂纹长/mXFEM解/(106N·m-1.5)解析解/(106N·m-1.5)相对误差/%0.150.77830.79191.720.251.09381.08171.120.351.40241.37811.760.451.74361.70262.410.552.13492.07113.080.652.58752.50323.37
3.2 裂纹扩展路径模拟
在计算模拟Ⅱ裂纹的裂纹扩展路径时,所取的XFEM计算模型中的网格密度、单元类型、裂纹位置与长度及材料参数与图7所示的XFEM计算模型的完全相同。为模拟II裂纹的裂纹扩展路径,设定的边界条件为:下侧边水平位移ux为-6.4 mm、上侧边水平位移ux为6.4 mm,上、下两边竖直位移uy均为0。
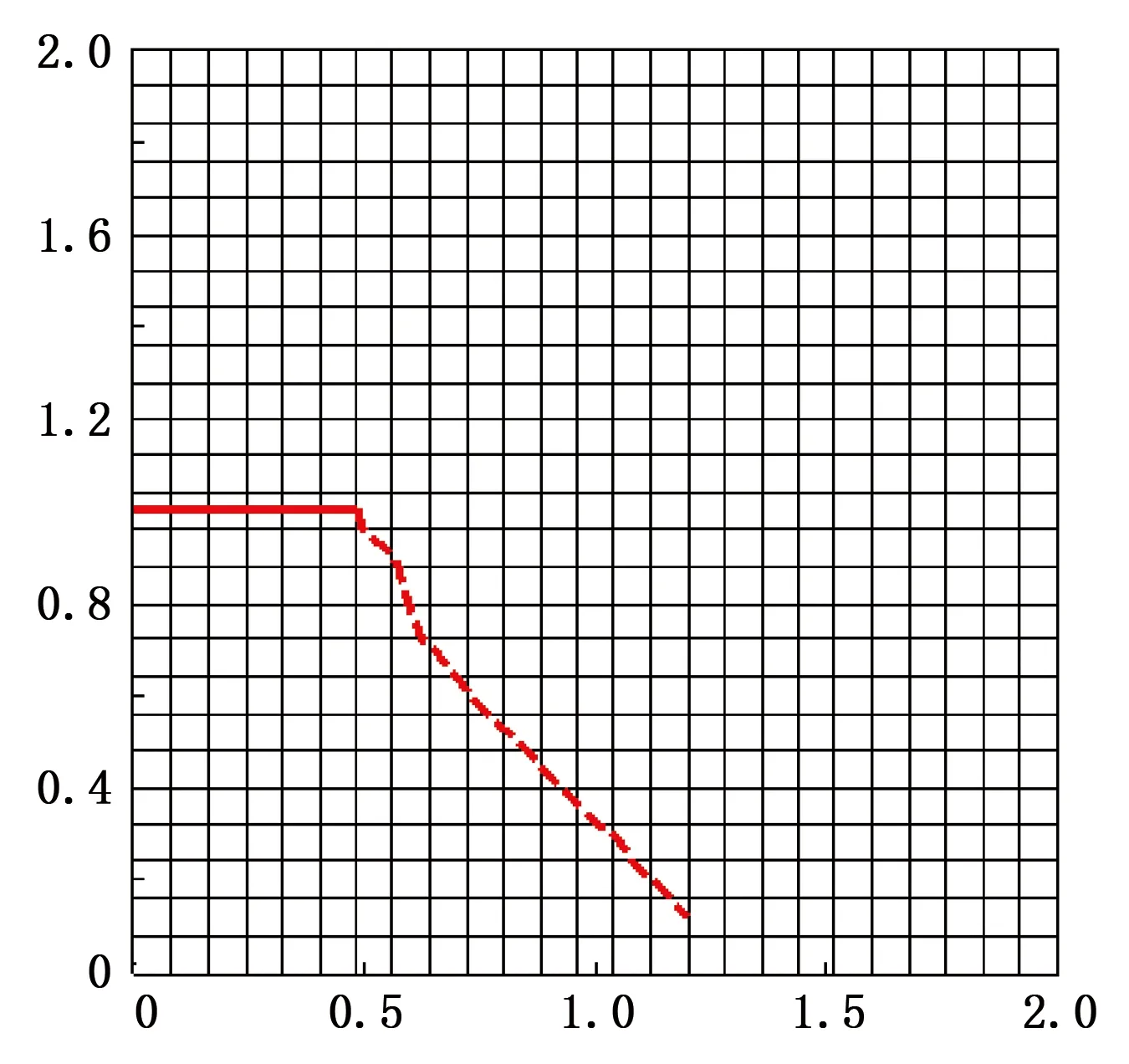
图8 由XFEM计算的Ⅱ型裂纹的裂纹扩展路径Fig.8 Crack propagation path of mode Ⅱ calculated by XFEM
图8为由XFEM计算得到的Ⅱ型裂纹的裂纹扩展路径,其中红色粗实线为初始裂纹的位置、红色粗虚线为裂纹的扩展路径。根据最大周向应力理论,即式(14)可知,Ⅱ型裂纹扩展的方向角θ0=-70.5°,图9所示的裂纹扩展方向与最大周向应力理论确定的裂纹扩展方向基本相同,可见XFEM能有效地预测裂纹的扩展路径。
图9为Ⅱ型裂纹扩展后的XFEM网格图,其中的结点位移被放大15倍,可以发现其变形规律和所设定的边界条件完全符合,数值计算结果是合理的,这也表明XFEM能有效地预测平面裂纹的扩展路径。
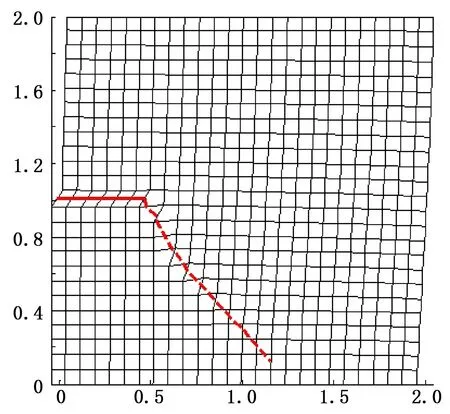
图9 Ⅱ型裂纹扩展后的XFEM网格图Fig.9 XFEM mesh figure after crack of mode Ⅱ propagating
4 结束语
阐述了单元位移模式选择、描述裂纹几何的水平集法及特殊单元的数值积分方法,建立了描述岩石断裂力学特性的扩展有限元法。建立的岩石断裂力学扩展有限元法可对岩石材料的断裂力学参数和裂纹扩展路径进行数值模拟计算,能有效地描述岩石断裂力学特性。XFEM计算模型验证了数值计算结果的合理性,可有效地预测平面裂纹的扩展路径。
[1] 李录贤,王铁军. 扩展有限元法(XFEM)及其应用 [J].力学进展, 2005,35(1):5-20.
LI Luxian, WANG Tiejun. The extended finite element method and its applications—a review [J]. Advances in Mechanics, 2005,35(1):5-20.
[2] 王承强,郑长良. 裂纹扩展过程中线性内聚力模型计算的半解析有限元法 [J]. 计算力学学报,2006,23(2):164-151.
WANG Chengqiang, ZHENG Changliang. Semi-analytical finite element method for linear cohesive force model in crack propagation [J]. Chinese Journal of Computational Mechanics, 2006,23(2):164-151.
[3] 孙玉周,王锦燕,许君风. 边界元法在断裂力学数值计算中的应用研究 [J]. 中原工学院学报,2004,15(5):21-23.
SUN Yuzhou, WANG Jinyan, XU Junfeng. Boundary element method for the plane elastic problem with cracks [J]. Journal of Zhongyuan Institute of Technology, 2004,15(5):21-23.
[4] 张雄,宋康祖,陆明万. 无网格法研究进展及其应用 [J]. 计算力学学报,2003,20(6):730-742.
ZHANG Xiong, SONG Kangzu, LU Mingwan. Research progress and application of meshless method [J]. Chinese Journal of Computational Mechanics, 2003,20(6):730-742.
[5] 孙翔,刘传奇,薛世峰. 有限元与离散元混合法在裂纹扩展中的应用[J]. 中国石油大学学报(自然科学版),2013,37(3):126-130.
SUN Xiang, LIU Chuanqi, XUE Shifeng. Application of combined finite-discrete element method for crack propagation [J]. Journal of China University of Petroleum(Edition of Natural Science), 2013,37(3):126-130.
[6] 顾元通,丁桦. 无网格法及其最新进展 [J]. 力学进展,2005,35(3):323-337.
GU Yuantong, DING Hua. Recent developments of meshless method [J]. Advances in Mechanics, 2005,35(3):323-337.
[7] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing [J].International Journal for Numerical Method in Engineering, 1999,45(5):601-620.
[8] MOES N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without without remeshing [J]. International Journal for Numerical Method in Engineering, 1999,46(1):131-150.
[9] MOSE N, BELYTSCHKO T. Extended finite element method for cohesive crack growth [J]. Engineering Fracture Mechanics, 2002,69(7):813-833.
[10] 余天堂.含裂纹体的数值模拟[J].岩石力学与工程学报,2005,24:4432-4439.
YU Tiangtang. Numerical simulation of a body with cracks [J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24:4432-4439.
[11] 方修君,金峰,王进廷.基于扩展有限元法的粘聚裂纹模型[J].清华大学学报(自然科学版),2007,47(3):344-347.
FANG Xiujun, JIN Feng, WANG Jinting. Cohesive crack model based on extended finite element method [J]. Journal of Tsinghua University (Science & Technology), 2007,47(3):344-347.
[12] 董玉文,余天堂,任青文.直接计算应力强度因子的扩展有限元法[J].计算力学学报,2008,25(1):72-77.
DONG Yuwen, YU Tiantang, REN Qingwen. Extended finite element method for direct evaluation of strength intensity factors [J]. Chinese Journal of Computational Mechanics, 2008,25(1):72-77.
[13] 宋娜,周储伟.扩展有限元裂尖场精度研究[J].计算力学学报,2009,26(4):544-547.
SONG Na, ZHOU Chuwei. Accuracy study of crack tip field in extended finite element method [J]. Chinese Journal of Computational Mechanics, 2009,26(4):544-547.
[14] 茹忠亮,朱传锐,张友良,等.裂纹问题的扩展有限元法研究[J].岩土力学,2011,32(7):2171-2176.
RU Zhongliang, ZHU Chuanyue, ZHANG Youliang,et al. Study of fracture problem with extended finite element method [J]. Rock and Soil Mechanics, 2011,32 (7):2171-2176.
[15] 师访,高峰,杨玉贵.正交各向异性岩体裂纹扩展的扩展有限元法研究[J].岩土力学,2014,35(4):1203-1210.
SHI Fang, GAO Feng, YANG Yugui. Application of extended finite element method to study propagation problems of orthotropic rock mass [J]. Rock and Soil Mechanics, 2014,35(4):1203-1210.
[16] 庄茁,柳占立,成斌斌,等. 扩展有限单元法 [M]. 北京:清华大学出版社,2012:35-46.
[17] 解德,钱勤,李长安.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009.
[18] ZHOU B, WANG D X, XUE S F. Calculation on crack parameter by extended finite element method [J]. Applied Mechanics and Materials, 2015(716/717):751-754.
(编辑 沈玉英)
Extended finite element method for fracture mechanics of rock
ZHOU Bo, SUN Bo, XUE Shifeng
(CollegeofPipelineandCivilEngineeringinChinaUniversityofPetroleum,Qingdao266580,China)
An extended finite element method (XFEM) was used to study the mechanical characteristics and crack propagation behaviors of rock materials, in which the methods for selecting the element displacement mode, the geometric description of plane cracks and the integration of special elements were introduced. The criteria for crack propagation in terms of the maximum hoop stress and an interaction integration method for calculating the stress intensity factor were introduced to formulate the fundamentals of the XFEM model in fracture mechanics of rocks. Then the XFEM model was developed to predict the mechanical behaviors of fractures in rocks, and the model was solved numerically using the MATLAB software. The stress intensity factors of the crack type I and the crack propagation paths of the crack type II were calculated and analyzed using the XFEM model, respectively. The calculation results show that the proposed XFEM method is viable to effectively simulate the crack propagation process and to calculate the fracture mechanics parameters in rock materials.
extended finite element method; level set method; stress intensity factor; interaction integral method;crack propagation criteria; crack propagation path
2015-10-22
国家自然科学基金项目(11472309);中石油重大专项(2012-ZG-002)
周博(1972-),男,教授,博士,博士生导师,研究方向为石油工程力学、智能材料与结构等。E-mail:zhoubo@upc.edu.cn。
1673-5005(2016)04-0121-06
10.3969/j.issn.1673-5005.2016.04.016
O 346.1
A
周博,孙博,薛世峰.岩石断裂力学的扩展有限元法[J].中国石油大学学报(自然科学版),2016,40(4):121-126.
ZHOU Bo, SUN Bo, XUE Shifeng. Extended finite element method for fracture mechanics of rock[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(4):121-126.

