基于迭代算法的磨料颗粒加速机制研究

左伟芹, 王晓川, 郝富昌, 卢义玉, 刘明举

(1.河南理工大学瓦斯地质与瓦斯治理国家重点实验室培育基地,河南焦作 454000;2.武汉大学水射流理论与新技术湖北省重点实验室,湖北武汉 430072;3.重庆大学煤矿灾害动力学与控制国家重点实验室,重庆 400030)



基于迭代算法的磨料颗粒加速机制研究

左伟芹1,2, 王晓川2, 郝富昌1, 卢义玉3, 刘明举1

(1.河南理工大学瓦斯地质与瓦斯治理国家重点实验室培育基地,河南焦作 454000;2.武汉大学水射流理论与新技术湖北省重点实验室,湖北武汉 430072;3.重庆大学煤矿灾害动力学与控制国家重点实验室,重庆 400030)

在前混合射流磨料加速机制研究中一般将阻力系数当作常数且忽略巴西特力的影响。针对这一问题,采用实时对比插值法分析阻力系数且考虑巴西特力对磨料加速的影响,在此基础上建立磨料运动微分方程,并通过迭代算法进行求解,较为全面、准确地阐释磨料加速机制。结果表明:在管道及喷嘴直线段内磨料受力由大到小分别为黏性阻力、巴西特力、视质量力,在喷嘴收敛段内磨料受力由大到小分别为压强梯度力、视质量力、黏性阻力、巴西特力,且全程中巴西特力都有不可忽略的影响;在喷嘴收敛段前半段磨料加速度大于液相加速度,在收敛段后半段磨料加速度略小于液相加速度,在喷嘴直线段内磨料加速趋缓。

前混合磨料射流; 加速机制; 巴西特力; 迭代算法

磨料水射流技术具有冷态、点割、通用性强、切割质量好、切割性能强和环保无污染等特点,在工业切割、隧道掘进、表面清洗和钻探开采等方面有广泛的应用[1-3]。前混合磨料射流的主要优势在于其具备超强的切割、冲蚀性能,而影响切割、冲蚀性能的关键因素之一是水介质对磨料的加速性能。磨料水射流存在着复杂的脉动现象,磨料在加速过程中受多种力的影响,其加速机制极为复杂。左伟芹等[4-6]采用实验手段对磨料射流进行了研究。张永利等[7-11]采用数值模拟的方法对磨料射流进行了研究。但由于磨料射流存在复杂的脉动现象,数值模拟所得的结果与磨料射流的真实流场还有一定的差距。李宝玉等[12-15]对单颗磨料进行受力分析,进而建立磨料的运动方程。这些研究大都将阻力系数这一关键参数当常数处理,且未考虑巴西特力对磨料加速的影响。为此,笔者提出运用实时对比插值法分析阻力系数且考虑巴西特力对磨料加速的影响,进而建立磨料运动微分方程,采用迭代算法对微分方程进行求解,更全面准确地阐释磨料加速机制。

1 磨料受力分析

磨料在加速的过程中主要受到的力为:黏性阻力、视质量力、巴西特力、压力梯度力、Magnus(马格努斯)升力和Saffman(沙夫曼)升力。根据牛顿第二运动定律,磨料运动微分方程式的欧拉形式可表示为

(1)

式中,rp为磨料半径;ρ为密度;V为速度;t为时间;CD为阻力系数;S为磨料的迎风面积;tp0为颗粒开始加速的时刻;tp为迭代终止时间;p为液体压力;x为位移;下标f表示液相,下标p表示磨料。

式(1)中第一项为黏性阻力,第二项为视质量力,第三项为巴西特力,第四项为压强梯度力,第五项为马格努斯升力,第六项为沙夫曼升力。

2 磨料在高压管道内的加速机制

2.1 迭代算法

在前混合磨料射流中,磨料颗粒在高压磨料罐流态化后从控制阀经混合腔进入高压管路中的主流后,由于磨料颗粒与高压水的流速不等,必将产生相互作用力,磨料颗粒受到第一次加速。进行如下几点假设:

(1)前混合磨料射流体积分数约为5%,按照十分稀疏的固液两相流考虑,忽略磨料颗粒之间的相互作用力。

(2)磨料为刚性球体。

磨料在高压管道内主要受黏性阻力、视质量力、巴西特力的影响。因此,磨料颗粒在高压管道内运动微分方程式的欧拉形式为

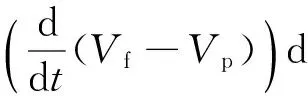
(2)

设第i步时磨料的速度为Vi。

2.1.1 计算黏性阻力

CD是阻力计算中的关键参数,该参数选取的精度直接影响阻力计算的结果。对于阻力系数CD,由于球形颗粒表面的附面层非常复杂,只有极少数特殊情况可从方程组导出计算式。目前,阻力系数主要依靠实验来确定。经过大量实验得到的单个刚性球体在静止、等温、不可压缩及无限大流场的流体中作匀速运动时的阻力系数与雷诺数之间的关系(称为标准阻力曲线),如图1所示。

将阻力系数作为常数或用某一公式来代替,在一定程度上影响计算精度。为消除这一影响,采用实时对比插值法进行分析。利用matlab对图片识别的功能,对图1进行处理,建立CD随着雷诺数变化的数据库。根据磨料速度Vi计算当前雷诺数,并在数据库内逐一对比,在当前雷诺数前后分别选取3组数据。根据该6组数据,采用三次样条插值法求当前雷诺数对应的阻力系数CDi,则黏性阻力可表示为

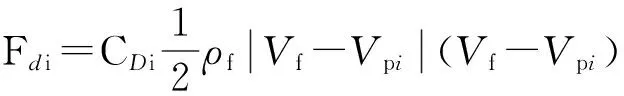
(3)

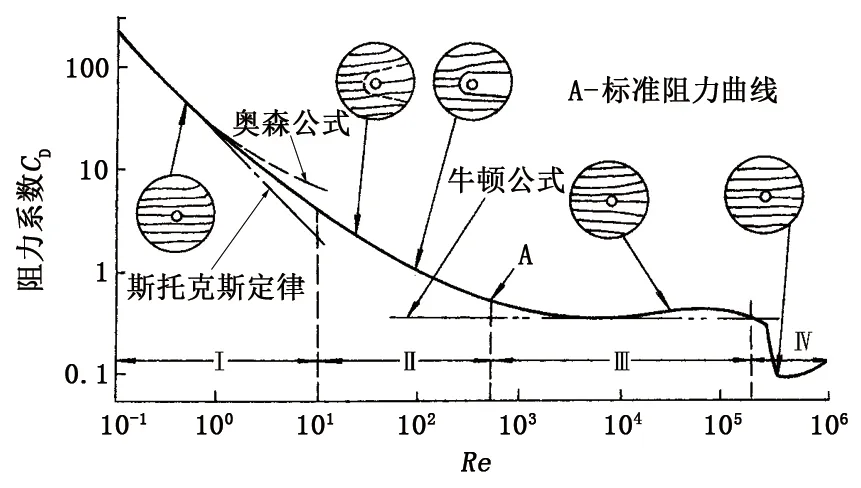
图1 圆球扰流阻力系数与雷诺数的关系曲线Fig.1 Relationship between viscous resistance coefficient of sphere and Reynolds number

2.1.2 计算巴西特加速度力

巴西特力是一个与磨料加速历程有关的力。设tp0=0,计算到第i步时,tpi=iΔt,τ=nΔt,则有:

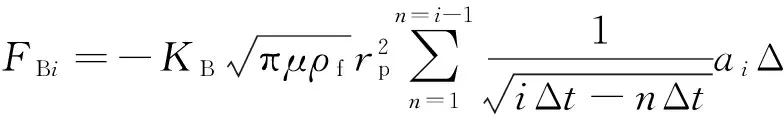
(4)

2.1.3 计算磨料加速度

在高压管道中,假设高压水的速度Vf为常数,视质量力可表示为

(5)

联立式(2)和式(5),可得加速度表达式如下:

(6)

根据加速度计算第i+1步时磨料的速度Vi+1及位移si+1,并将相关参数带入迭代算法继续进行循环计算。

2.2 算例分析

在流量为50 L/min,高压管道直径为20 mm,磨料类型为陶粒,磨料尺寸为0.841 mm,磨料视密度为2.7 kg/L,动力黏性系数为1.14×10-3kg·m-1·s-1,时间步长取0.000 02 s,总步长为20 000进行计算,计算结果如图2所示。

由图2看出,磨料经过0.2 m的加速,其速度已经达到了液相的88.5%;经过0.8 m的加速后,其速度已经达到液相的92.6%;之后磨料依然在加速,磨料速度无限接近液相的速度。如图3所示为磨料加速过程中各力随位移的变化关系。

由图3看出,磨料在管道内加速时,黏性阻力Fd始终与磨料运动方向一致,在磨料加速过程中起到了主要作用。视质量力Fm、巴西特力FB均与磨料运动方向相反,起到了阻碍磨料加速的作用。在磨料加速过程中,视质量力Fm迅速衰减渐并逐渐趋近于0。黏性阻力和巴西特力虽然也在衰减,但衰减速度不快。在加速的后期主要受到了黏性阻力和巴西特力的影响,但两者方向相反。随着磨料加速两者之差逐渐减小,故磨料加速度也在迅速衰减,但磨料与液相的速度依然在无限靠近。

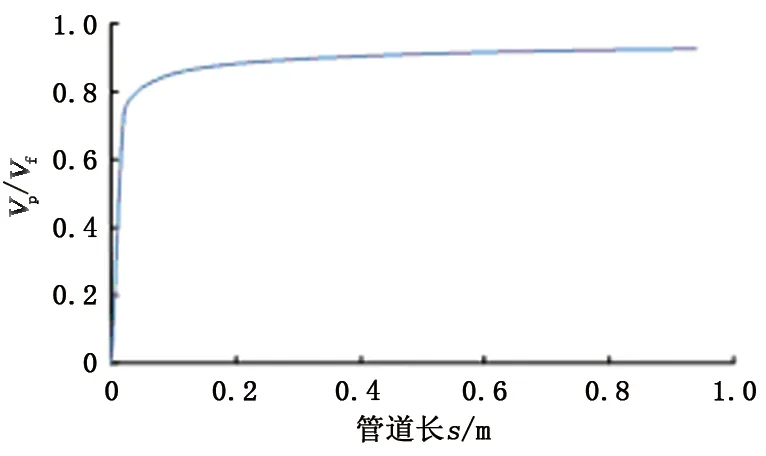
图2 高压管道内磨料与液相速度比分布Fig.2 Distribution of velocity ratio of abrasive to water phase in high pressure pipe

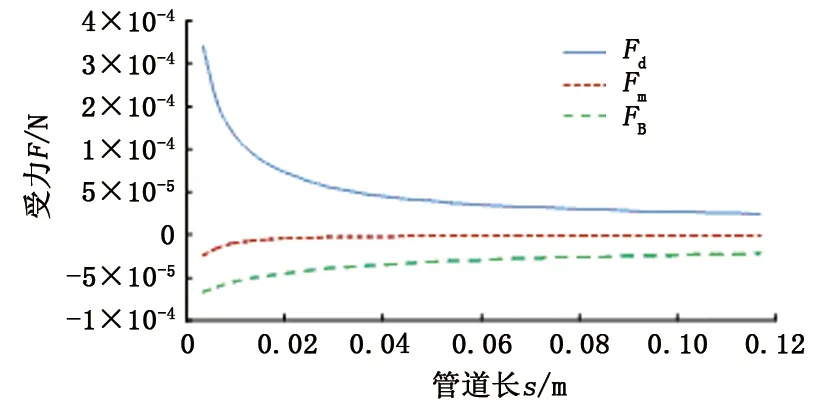
图3 高压管道内磨料受力分布Fig.3 Abrasive stress distribution in high pressure pipe

3 磨料在喷嘴内的加速机制

磨料在高压管道内完成了第一次加速。但由管道内流速不大,磨料获得的动能较小。磨料第二次加速是在喷嘴内完成的。

3.1 迭代算法

磨料在喷嘴直线段内主要受到黏性阻力、视质量力、巴西特力的影响,其算法与磨料在管道内一致,在此不再赘述。磨料在喷嘴收敛段内不仅受到上述三个力,还受到了压强梯度力的影响,其运动微分方程的欧拉形式可表示为

(7)

设第i步时,磨料的速度为Vi。压强梯度力是由于压强梯度引起的附加压强分布的不均匀性形成的力,其中∂p/∂x为该力的关键参数。图4为在位移dx上压强变化示意图。

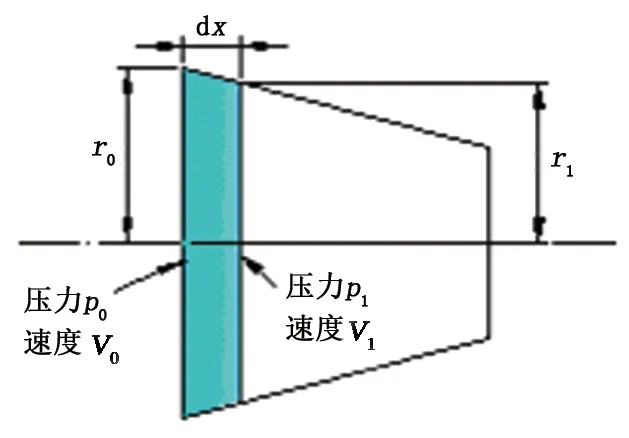
图4 喷嘴收敛段内压强变化示意图Fig.4 Sketch map of pressure change in nozzles convergence section

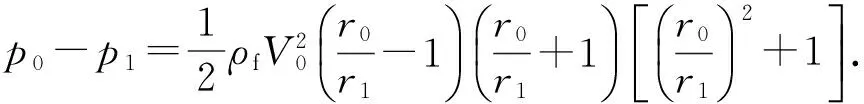
(8)

由于dx相对于r0为无穷小,式(8)可简化为

(9)

因此,压强梯度力可表示为

(10)

则加速度表达式如下:

(11)

根据加速度计算第i+1步时磨料的速度Vi+1及磨料的位移si+1,当磨料位移si+1大于喷嘴收敛段长度时停止计算,当磨料位移si+1小于喷嘴收敛段长度时继续进行循环计算。磨料在喷嘴直线段内加速时,按照迭代算法计算,磨料位移大于喷嘴直线段长度时迭代结束。

3.2 算例分析

算例分析的条件:流量为50 L/min、高压管道直径为20 mm、磨料类型为陶粒、磨料尺寸为0.841 mm、磨料视密度为2.7 kg/L、动力黏性系数为1.14×10-3kg·m-1·s-1、时间步长为0.000 02 s、总步长为20 000、喷嘴直径为3 mm、收敛段长度为23 mm、直线段长度为11、收敛角为14°。假设磨料在高压管道内加速较为充分,将管道内液相的速度视为磨料在喷嘴入口处的初始速度。将上述参数代入迭代程序进行计算,结果如图5所示。

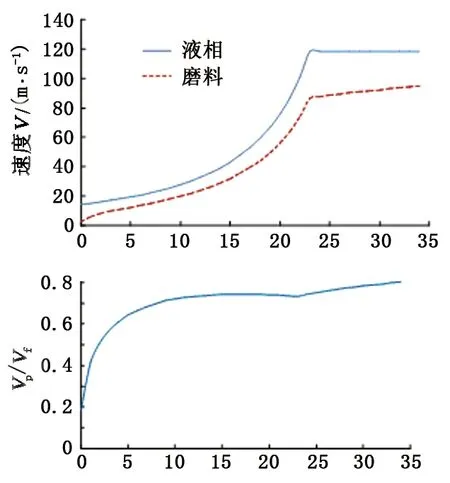
图5 喷嘴内磨料相与液相速度对比曲线Fig.5 Velocity contrast curve of abrasive to water phase in nozzle

由图5看出:在收敛段内液相加速的同时磨料速度也得到了很大的提升,在喷嘴收敛段前半段,液相速度不高,磨料速度提升不快,在收敛段后半段,液相速度急剧增加的同时磨料速度也急剧提升;在位移小于10 mm之前,磨料和液相速度迅速接近,表明磨料加速度大于液相加速度。因为在收敛段前半段,过流面积变化趋势缓慢,液相加速较慢,且磨料初始速度较低,磨料速度与液相速度之间有较大的差值导致磨料加速度大于液相加速度。而在收敛段后半段,液相速度急剧增加,磨料加速延迟,故在15 mm后速度比有所下降。在直线段内,液相速度不变,磨料依然处于加速状态,在喷嘴出口处磨料速度达到了液相的80%,磨料速度与液相速度之间依然有一定的差距。如图6为磨料加速过程中各力随位移的变化关系。

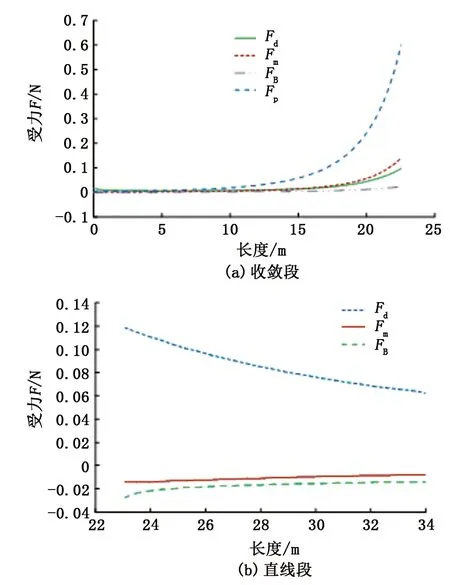
图6 喷嘴内磨料受力分布Fig.6 Stress distribution of abrasive in nozzle

由图6可知:磨料在喷嘴收敛段内受力由大到小分别为压强梯度力、视质量力、黏性阻力、巴西特力,其中压强梯度力起到了主要作用;磨料在喷嘴直线段内受力由大到小依次为黏性阻力、巴西特力、视质量力,其中黏性阻力与磨料运动方向一致,在加速过程中起到了主要作用。视质量力、巴西特力均与加速度方向相反,起到了阻碍加速的作用。由式(7)可知,黏性阻力与磨料和液相的速度差有关,故随着磨料的加速黏性阻力明显减小,而视质量力及巴西特力与磨料的加速度有关,因在直线段内磨料的加速度变化不大,故视质量力与巴西特力变化不大。综上分析可知磨料在喷嘴直线段内加速较为缓慢。

4 结 论

(1)采用实时对比插值法分析阻力系数且考虑巴西特力,建立磨料运动微分方程,并利用迭代算法进行求解,可对磨料加速机制进行较为全面和准确的阐释。

(2)在管道及喷嘴直线段内磨料受力由大到小分别为黏性阻力、巴西特力、视质量力,在喷嘴收敛段内磨料受力由大到小分别为压强梯度力、视质量力、黏性阻力、巴西特力,在磨料加速全程中巴西特力都有不可忽略的影响。

(3)在喷嘴收敛段内磨料与液相同时加速,在收敛段前半段磨料加速度大于液相加速度,在收敛段后半段磨料加速度略小于液相加速度,在喷嘴直线段内磨料加速较为缓慢。

[1] 向文英,李晓红,卢义玉,等.淹没磨料射流的岩石冲蚀实验研究[J].中国矿业大学学报,2009,38(2):240-243.

XIANG Wenying, LI Xiaohong, LU Yiyu, et al. Experimental study of domino effect on submerged abrasive water jets[J]. Journal of China University of Mining & Technology, 2009,38(2):240-243.

[2] 康勇,王晓川,卢义玉,等.磨料射流辅助三翼钻头破岩实验研究[J].中国矿业大学学报,2012,41(2):212-218.

KANG Yong, WANG Xiaochuan, LU Yiyu, et al. Experimental study of rock breaking by a three wing abrasive jet assisted drill bit[J]. Journal of China University of Mining & Technology, 2012,41(2):212-218.

[3] 左伟芹,卢义玉,赵建新,等.实验研究喷嘴磨损规律的新方法[J].四川大学学报(工程科学版),2012,44(1):196-200.

ZUO Weiqin, LU Yiyu, ZHAO Jianxin, et al. The novel idea ofexperiment study on the wear mechanism of nozzles[J].Journal of Sichuan University:Engineering Science Edition,2012,44(1):196-200.

[4] 左伟芹.前混合磨料射流磨料加速机制及分布规律[D].重庆:重庆大学,2012.

ZUO Weiqin. Abrasive accelerated mechanisms and distribution law in pre-mixed abrasive jet[D]. Chongqing:Chongqing University,2012.

[5] STEVENSON A N J, HUTCHINGS I M. Scaling laws for particle velocity in the gas-blast erosion test[J]. Wear,1995,181-183:56-62.

[6] LIU H T, MILES P J, COOKSEY N, et al. Measurements of water-droplet and abrasive speeds in a ultrahigh-pressure abrasive-water jets[C]. Houston:the 10th American Water jet Conference,1999.

[7] 张永利,于欢,马玉林.磨料射流固液两相流场的数值模拟[J].辽宁工程技术大学学报(自然科学版),2011,30(3):385-388.

ZHANG Yongli,YU Huan,MA Yulin. Numerical simulation of liquid-solid two phase flow field for abrasive water jet[J]. Journal of Liaoning Technical University(Natural Science),2011,30(3):385-388.

[8] 王荣娟,雷玉勇,蒋代君，等.磨料水射流喷头内部流场仿真及聚焦管参数分析[J].煤矿机械,2011,32(8):61-63.

WANG Rongjuan, LEI Yuyong, JIANG Daijun, et al. Simulation of flow field inside cutting head of abrasive water jet and analysis of parameters of focusing tube[J]. Coal Mine Machinery,2011,32(8):61-63.

[9] 姜玉颖,龚烈航,徐新林，等.磨料水射流喷嘴内流场数值模拟[J].兵工学报,2014,35(4):461-467.

JIANG Yuying, GONG Liehang, XU Xinlin, et al. Numerical simulation of flow field in abrasive water jet nozzles[J]. Acta Armamentarii,2014,35(4):461-467.

[10] 向文英,卢义玉,李晓红.淹没磨料射流场模拟计算分析[J].四川大学学报(自然科学版), 2008,45(4):929-934.

XIANG Wenyin, LU Yiyu, LI Xiaohong. The analyse of numerical simulation of abrasive water jets submerged[J]. Journal of Sichuan University:Natural Science Edition,2008,45(4):929-934.

[11] 陈林, 雷玉勇,郭宗环,等.基于 FLUENT 的后混合磨料水射流喷嘴内流场的数值模拟[J].润滑与密封,2012,37(4):66-69.

CHEN Lin, LEI Yuyong, GUO Zonghuan, et al. Numerical simulation of post-mixed abrasive water jet nozzle based on FLUENT[J]. Lubric Ation Engineering,2012,37(4):66-69.

[12] 李宝玉,郭楚文.用于煤矿安全切割的前混合磨料射流加速机制研究[J].中国安全科学学报,2005,15(4):52-55.

LI Baoyu, GUO Chuwen. Study on acceleration mechanism of abrasive particles of DIA jet in coalmine safe cutting[J]. China Safety Science Journal,2005,15(4):52-55.

[13] 铁占绪.磨料射流中磨料例子的加速机制和运动规律[J].焦作矿业学院学报,1995,14(4):39-54.

TIE Zhanxu. The acceleration mechanism and movement pattern of the particle in the abrasive water jet[J]. Journal of Jiaozuo Mining Institute,1995,14(4):39-54.

[14] 董星.前混合式磨料水射流磨料颗粒运动的理论分析[J].黑龙江科技学院学报,2001,11(3):4-6.

DONG Xing. The theoretical analysis of grain movement of DIA jet abrasive water jet[J]. Journal of Heilongjiang Institute of Science,2001,11(3):4-6.

[15] 杨国来,李强,陈俊远,等.磨料喷嘴内磨料颗粒加速机制分析[J].机床与液压,2011,19(29):54-58.

YANG Guolai, LI Qiang, CHEN Junyuan, et al. The acceleration mechanism analysis of the abrasive in the abrasive water-jet nozzle[J]. Machine Tool & Hydraulics,2011,19(29):54-58.

(编辑 刘为清)

Research on acceleration mechanism of abrasive in pre-mixed abrasive water-jet based on iterative algorithm

ZUO Weiqin1,2, WANG Xiaochuan2, HAO Fuchang1, LU Yiyu3, LIU Mingju1

(1.StateKeyLaboratoryCultivationBaseforGasGeologyandGasControl,HenanPolytechnicUniversity,Jiaozuo454000,China; 2.HubeiKeyLaboratoryofWaterjetTheoryandNewTechonology,HenanPolytechnicUniversity,Wuhan430072,China; 3.StateKeyLaboratoryofCoalMineDisasterDynamicsandControl,ChongqingUniversity,Chongqing400030,China)

It has been reported that the resistance coefficient was treated as constants and the basset acceleration force was often ignored on the acceleration mechanism of abrasive in pre-mixed abrasive water-jet. Aiming at this issue, the contrast analysis of real-time interpolation method were used to analysis the viscous resistance coefficient and the influence of basset force on the abrasive acceleration was considered. And the differential equation of motion for abrasive was established, which was solved by the iterative algorithm. The research results show that the forces acting on abrasive from large to small is as follows: viscous resistance, basset acceleration force, and apparent mass force in the high pressure pipe and the straight line segment of nozzle. The forces acting on abrasive from large to small is as follows: pressure gradient force, apparent mass force, viscous resistance, and basset acceleration force in the convergence segment of nozzle, in which the basset acceleration force plays an important role in the whole course. The acceleration of abrasive is faster than liquid in front half part of the convergence segment. However, in behind half part of the convergence segment the acceleration of abrasive is slower than liquid, and abrasive accelerates slowly in the straight line segment.

premixed abrasive jet; acceleration mechanism; basset acceleration force; iterative algorithm

2015-11-23

国家自然科学基金项目(51404099);武汉大学水射流理论与新技术湖北省重点实验室开放课题(HBKLWJ-2014F04);国家安监局项目(henan-0037-2015AQ,henan-0032-2015AQ)

左伟芹(1984-),男,讲师,博士,研究方向为高压水射流理论及其应用。E-mail:zuoweiqin@163.com。

郝富昌(1981-),男，副教授,博士,研究方向为瓦斯灾害预测与防治。E-mail:haofuchang@163.com。

1673-5005(2016)04-0104-06

10.3969/j.issn.1673-5005.2016.04.013

TE 248

A

左伟芹,王晓川,郝富昌,等.基于迭代算法的磨料颗粒加速机制研究[J].中国石油大学学报(自然科学版)，2016,40(4)：104-109.

ZUO Weiqin, WANG Xiaochuan, HAO Fuchang, et al. Research on acceleration mechanism of abrasive in pre-mixed abrasive water-jet based on iterative algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(4):104-109.