甲烷水合物热导率分子动力学模拟及分析

杨德伟， 刘雨文， 修 毓, 徐宏国， 苑昆鹏，徐 哲

(1.中国石油大学储运与建筑工程学院, 山东青岛 266580; 2.中国石化胜利油田分公司滨南采油厂,山东滨州 256600；3.山东省青岛市黄岛区城市建设局工程建设管理中心,山东青岛 266555)



甲烷水合物热导率分子动力学模拟及分析

杨德伟1， 刘雨文2， 修 毓3, 徐宏国2， 苑昆鹏1，徐 哲1

(1.中国石油大学储运与建筑工程学院, 山东青岛 266580; 2.中国石化胜利油田分公司滨南采油厂,山东滨州 256600；3.山东省青岛市黄岛区城市建设局工程建设管理中心,山东青岛 266555)

采用平衡态分子动力学方法模拟分子甲烷水合物导热性能,结合声子态密度分析甲烷分子和水分子间的能量耦合过程;探究范德华相互作用对热导率温度相关性的影响。结果表明:热导率随着甲烷分子和水分子间范德华相互作用的增强而增大。相互作用的增强令甲烷分子的振动峰值向高频区域移动,使得甲烷分子与水分子间的振动耦合作用增强,VDOS匹配程度增加,进而增大了甲烷水合物的热导率。高温下的温度相关性归因于弛豫时间声子的出现导致的非弹性散射,低温下主要受到光学声子模式和低频声子的约束影响。模拟的热导率的温度依赖性与实验结果吻合较好。

甲烷水合物; 分子动力学; 声子; 热导率

作为新能源的甲烷水合物是保证国家能源安全和保护环境而迫切需要解决的问题之一[1]。甲烷水合物不同于冰及其他分子晶体的是其热导率在接近德拜温度的高温区域表现出类似非晶体的特性,而在低温下呈现出晶体特性[2]。Jiang等[3-4]采用非平衡态分子动力学方法研究了温度在30～260 K甲烷、二氧化碳和xenon水合物的热导率。水合物热导率的温度相关性在温度低于50 K时与实验结果一致。English等[5-9]采用Green-Kubo方法研究了不同类型的甲烷水合物的热导率,并分析了长程静电力的处理对结果的影响。研究发现sI型甲烷水合物热导率变化的转变温度为90 K。甲烷水合物的热导率不仅与笼形结构的稳定性有关,还取决于甲烷分子和水分子间的相互作用。平衡态分子动力学方法(EMD)和非平衡态方法都是利用Green-Kubo 关系式积分热流自相关函数计算导热系数,该方法能够从平衡系统微小的温度波动中将导热系数提取出来。相比非平衡态方法,该方法由于使整个体系保持在同样的温度下,温度波动带来的误差相对小很多。不同的是平衡态方法在NVE系综(恒N、V、E系综)完成导热系数的计算,能够模拟真实的物理情景。笔者采用平衡态分子动力学方法模拟分子甲烷水合物导热性能,结合声子态密度分析甲烷分子和水分子间的能量耦合过程;探究范德华相互作用对热导率温度相关性的影响。

1 模 拟

1.1 物理模型及势函数

根据X射线衍射实验[10]结果构建1×1×1的sI型甲烷水合物晶胞,然后向X、Y、Z三个方向拓展成2×2×2的sI型甲烷水合物晶胞,如图1所示。模拟中3个方向上都采用周期性边界条件。由于甲烷水合物的声子平均自由程小于一个原胞的长度,因此大尺寸系统不会显现出显著的尺寸效应。

采用TIP4P[11]势能函数描述水分子之间的相互作用,甲烷采用OPLS[12]模型。目前常用的几种描述甲烷分子间的势能模型为:Tersoff势能、Brenner势能及Brenner势能基础上修正后的REBO势能等。Tersoff势能能够准确地模拟碳单键、双键、三键势能与键长的关系,但该势能在描述一些特殊成键(如空位)时与实际物理情况不符。后面两种势能均在对Tersoff势能修正的基础上发展起来,且第三种势能在第二种势能的基础上又做了进一步的修

正,但是这两种势能均须做大量的插值计算,长时间计算会降低结果的精度。通过对这三种势能的实际计算比较,发现在不考虑特殊成键的情况下,Tersoff势能在长时间的NVE循环中能更好地保持温度的恒定性,温度基本上在平衡值上下波动。故采用Tersoff型势函数模拟甲烷分子之间相互作用。模拟过程不考虑原子间长程库仑力的作用。Tersoff势能的表达式为

Vtersoff(rij)=fC(rij)[fR(rij)+bijfA(rij)].

(1)

式中,i,j为体系中的原子;rij为i,j原子成键键长;Vtersoff(rij)为i原子和其邻近原子j之间的作用能;fR、fA分别为产生作用能的排斥项和吸引项;fC为势能截取函数为bij为键序函数。

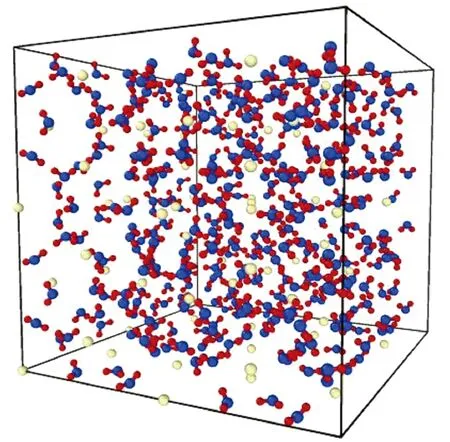
图1 2×2×2的sI型甲烷水合物晶胞Fig.1 Physical model of sI methane hydrate with size 2×2×2

Tersoff多体势能只考虑了近程原子的作用力,即当原子间距大于S=2.1 Å时,原子间的多体相互作用势能被截断。故在计算中,有时还要考虑远程力的作用,比如范德华力的作用。范德华作用势能,即Lennard-Jones势能的表达式为

(2)

式中,ε和σ分别为能量和距离参数;χ为标度系数,用来调整范德华作用力强弱。

不同种类的分子之间的势能参数可以采用Lorentz-Berthelot混合规则计算得出。本文中采用的分子间的L-J势能参数见表1。采用精度为1×10-4的PPPM方法计算长程静电力,截断半径为8.5 Å。采用Lennard-Jones(L-J)势能模型描述甲烷分子和水分子之间的相互作用,截断半径为10.0 Å。由于Tersoff势能在r为0.21 nm时已经为零,而Lennard-Jones势能在该处的值不为零,为了使势能曲线在整个空间光滑,需要在其衔接处做样条函数插值处理。

表1 分子间L-J势能参数

1.2 模拟方法及步骤

采用平衡态分子动力学方法(EMD)计算甲烷水合物热导率。EMD方法是利用基于线性响应理论的Green-Kubo公式计算热导率,其表达式为

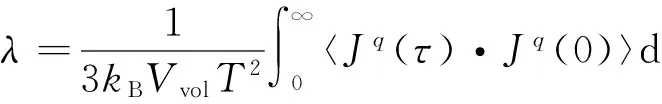
(3)

其中

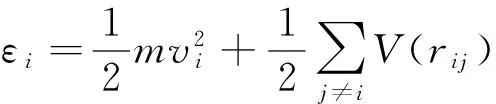
式中,λ为热导率,W/(m·k);V为系统的体积,m3;T为模拟温度,K;kB为Boltzmann常数;Jq(τ)为τ时刻的总热流,W·m;〈Jq(τ)·Jq(0)〉为热流自相关函数;εi为i原子的总能量,J。

采用Green-Kubo计算式计算导热系数,表示为

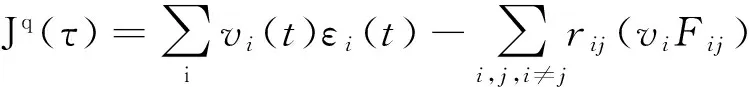
(4)

其中

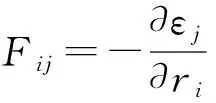
式中，Vi为i原子的速度。

考虑到并行计算和采用的势函数,采用分子动力学程序LAMMPS进行模拟[13]。首先采用共轭梯度算法对晶胞进行能量最小化,然后采用Nosé-Hoover热浴方法[14-15]使系统在NVT系综下弛豫100万步,调节系统到目标温度,之后转到NPT系综继续弛豫100万步,使系统达到平衡,然后再持续运行400万步统计热流并进行热导率的计算,以确保热流自相关函数收敛至零。模拟采用的时间步长为1 fs,运动方程的积分选用Velocity-Verlet算法。

2 模拟结果分析

2.1 热导率的温度相关性

图2给出了温度为200 K时热流自相关函数随时间的收敛情况。从图2可以看出,热流自相关函数在开始时迅速衰减并在零值附近振荡,在0.5 ps后逐渐收敛于零,表明在模拟时间内水合物的热导率已经收敛。

图3给出了客体甲烷分子100%填充和50%填充的水合物的热导率,同时给出了实验上采用瞬态面热源法的测量结果[5]。

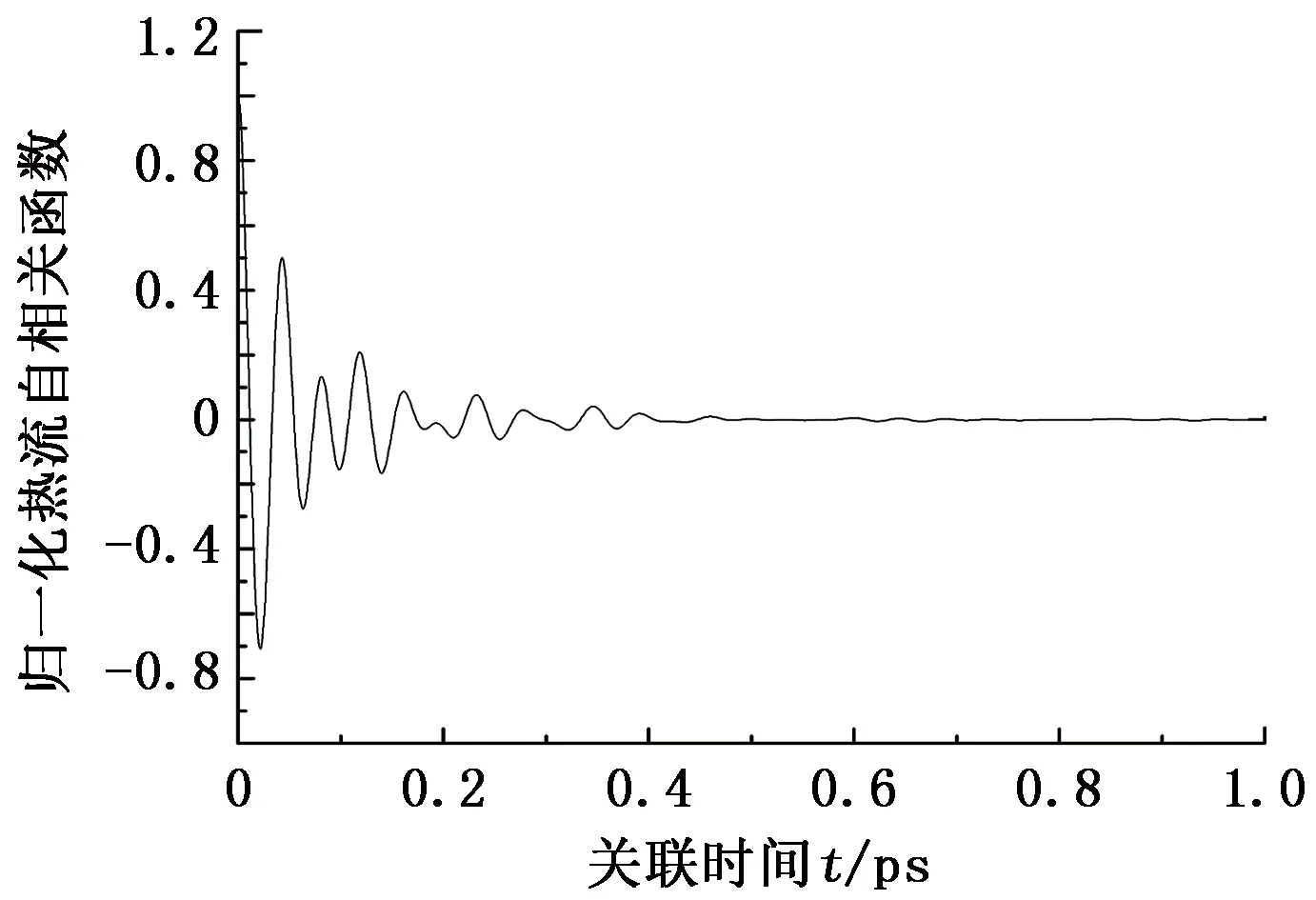
图2 200 K下归一化热流自相关函数随关联时间的变化Fig.2 Change of normalized heat current autocorrelation function with correlation time at temperature of 200 K

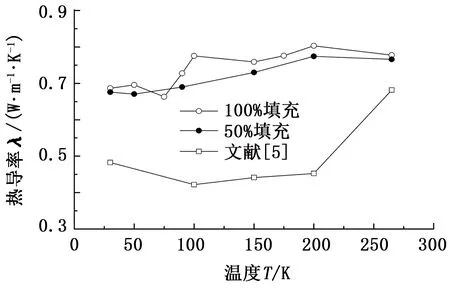
图3 0.1 MPa不同温度下甲烷水合物的热导率Fig.3 Computed thermal conductivities for methane hydrate at different temperature for pressure of 0.1 MPa

计算得到的100%填充的水合物的热导率在265 K时为0.75 W·m-1·K-1,比实验数据0.61 W·m-1·K-1高了10%,主要原因是合成的水合物试样存在孔隙,且在模拟过程中存在晶格缺陷等。当温度从265 K减小到100 K时,甲烷水合物的热导率随着温度减小,这是由于声子非弹性散射的减小导致能量传递通道减少,进而使得热导率减小。一个显著的特征是随着温度继续减小热导率开始增加。类似的行为也体现在实验结果中,但其幅值更小。然而,事实上很难直接和定量地比较分子动力学模拟结果和实验结果,因为实验结果与样品的特性和品质有关,例如孔隙度。此外,除了系统尺寸和静电力之外,势能函数的准确性也给比较带来了难度。在整个考虑的温度范围,100%填充率的甲烷水合物热导率比50%填充率的水合物的热导率大5%。晶格笼中包含甲烷分子导致了能量传递的增强,表明客体分子和主体分子间发生了更多的振动耦合,尽管这种趋势在模拟的误差范围内。计算的甲烷水合物的热导率在模拟的温度区间内对晶穴占有率不敏感。之前的分子动力学(MD)模拟也表明sI甲烷水合物的热导率与晶穴占有率的相关性很微弱。100%占有率的甲烷水合物的热导率行为主要归因于声子输运中的短程弛豫时间,即更短的声子平均自由程。这个发现意味着甲烷水合物和冰之间的晶格结构的不同起着更重要的作用,这与之前对甲烷水合物低热导率的解释不同。换句话说,甲烷分子与水笼子的碰撞可能激发了载热的声学声子模式,水分子的氢键网络比空笼水合物更疏松,导致新的声学模式的出现和能量的非局域化,导致热导率的升高。这种特殊的热行为可能是由于客体分子的相互作用引起的非简谐声学模式声子的振动。所以,热导率与空穴填充率的关系可以归因于非简谐声子运动的声子非弹性散射。

2.2 主客体分子间作用力强度的影响

为了研究客体甲烷分子和主体水分子间范德华作用强度对热导率的影响,分别计算了χ=1、2、3、4时甲烷水合物的热导率。温度为200 K、不同范德华作用强度下甲烷水合物的热导率见图4。

由图4可知,甲烷水合物的热导率随着客体分子和主体分子间范德华作用强度的增强而增加,表明热导率正比于甲烷分子和水分子间的相互作用强

度。当主客体分子间作用较弱时,笼状结构的对称性会约束甲烷分子在晶穴中的运动,使其运动局域在晶穴中心,有着最小的势能且相互间吸引力起主要作用，表明水分子被拉向晶穴的中心,导致晶格常数减小。随着温度和相互作用力强度的增加,客体分子的局域化特征减弱,更容易靠近晶穴附近的水分子,从而排斥水分子。甲烷分子在低温和低频区域与笼形水分子间的非简谐势能更加显著[16]。

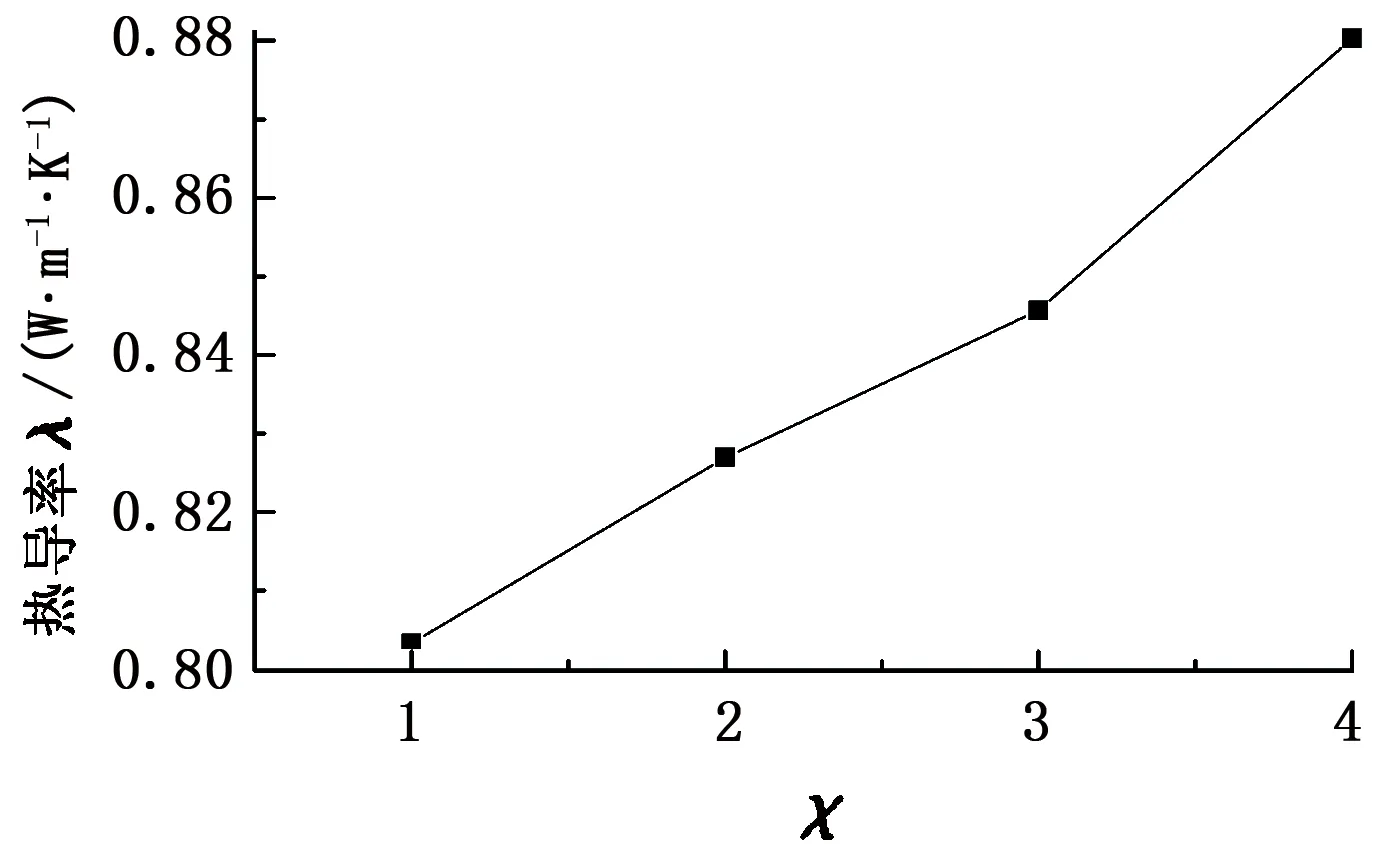
图4 200 K,0.1 MPa热导率随相互作用力强度χ的变化Fig.4 Computed thermal conductivities of methane hydrate for different values of χ at T=200 K,p=0.1 MPa

采用声子态密度(VDOS)表征不同频率声子振动模式的强弱,可由速度自相关函数(VACF)的傅立叶变换得到。图5为不同范德华作用强度下C原子和O原子的声子态密度。

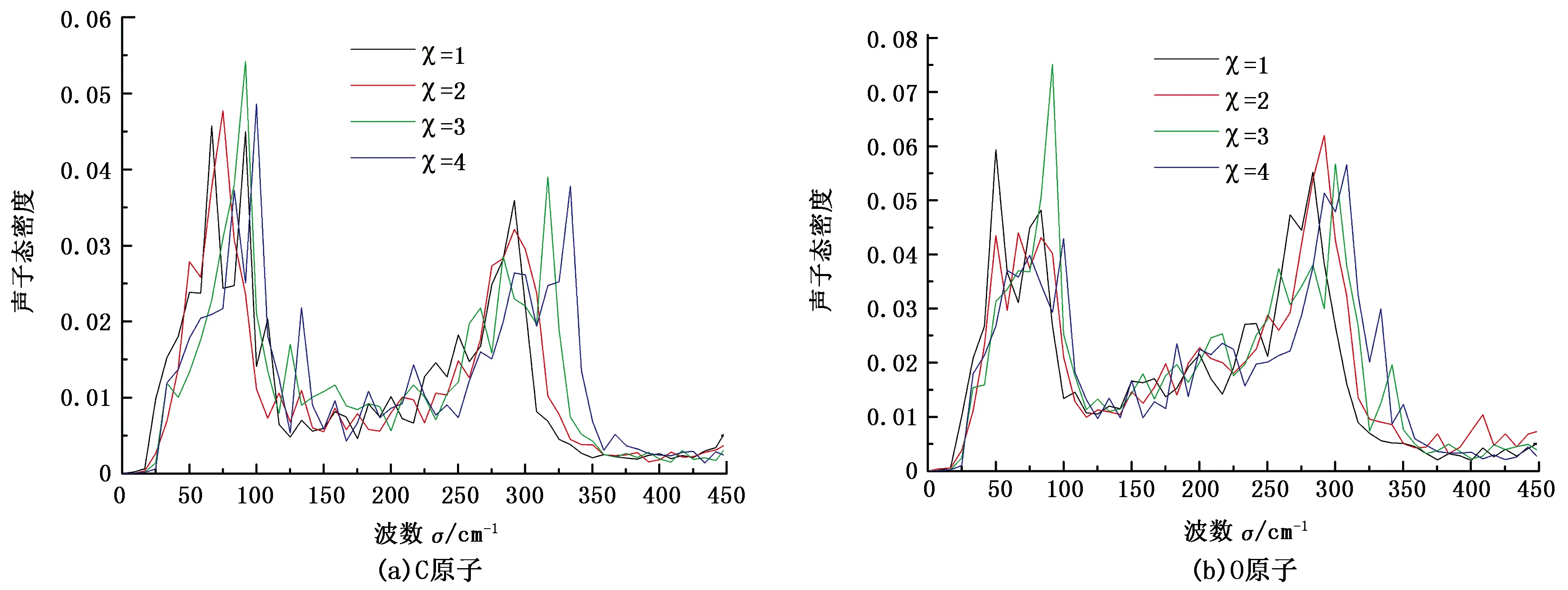
图5 不同范德华作用强度下C原子和O原子的声子态密度Fig.5 VDOS of carbon and oxygen atoms at different interaction strengths

由图5可知, C原子的振动峰值分别在50～100 cm-1和300 cm-1附近,甲烷的振动峰值与English等[8]的结果一致,分别对应于水合物中大晶穴和小晶穴中甲烷分子的振动。此外,甲烷分子的振动在低频区域局域化特征明显,而在高频区域局域化特征减弱。随着甲烷分子与水分子间范德华作用强度的增加,受到主客体分子间共振散射的影响,甲烷分子的振动峰值向高频区域移动。由图5(b)可见,不同主客体分子间范德华作用强度下O原子的VDOS变化不明显,其两个振动峰值分别为60 cm-1和300 cm-1。衡量C原子和O原子VDOS的重叠程度[17]的表达式为

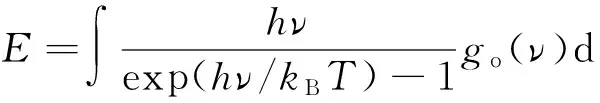
(5)

式中,E为VDOS重叠区域的声子能量,eV;h为普朗克常数,eV·s;ν为声子频率,Hz;kB为玻尔兹曼常数,eV/K;T为温度,K;go(v)为原子重叠的VDOS;hν为每个声子的能量,eV;1/(exp(hν/kBT)-1)为波色-爱因斯坦分布。

图6为χ下C原子和O原子VDOS重叠区域的能量。由图6可知,随着主客体分子间范德华作用的增强,C原子和O原子VDOS重叠区域的能量增加。这是因为主客体分子间范德华作用的增强令甲烷分子的振动峰值向高频区域移动,使得甲烷分子与水分子间的振动耦合作用增强,VDOS匹配程度增加,从而提高了甲烷水合物的热导率。

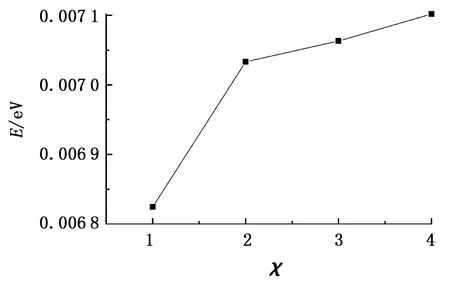
图6 不同χ下C原子和O原子VDOS重叠区域的能量Fig.6 Energy in VDOS overlapped region of carbon and oxygen atoms for different values of χ

3 结 论

(1)热导率随着甲烷分子和水分子间范德华相互作用的增强而增大。相互作用的增强令甲烷分子的振动峰值向高频区域移动,使得甲烷分子与水分子间的振动耦合作用增强,VDOS匹配程度增加,进而增大了甲烷水合物的热导率。

(2)高温下的温度相关性归因于弛豫时间声子的出现导致的非弹性散射,低温下主要受到光学声子模式和低频声子的约束影响。

[1] SLOAN E D. Fundamental principles and applications of natural gas hydrates[J]. Nature, 2003,426(6964):353-363.

[2] TSE J S, WHITE M A. Origin of glassy crystalline behavior in the thermal properties of clathrate hydrates: a thermal conductivity study of tetrahydrofuran hydrate[J]. The Journal of Physical Chemistry, 1988,92(17):5006-5011.

[3] JIANG H, MYSHAKIN E M, JORDAN K D, et al. Molecular dynamics simulations of the thermal conductivity of methane hydrate[J]. The Journal of Physical Chemistry B, 2008,112(33):10207-10216.

[4] JIANG H, JORDAN K D. Comparison of the properties of xenon, methane, and carbon dioxide hydrates from equilibrium and nonequilibrium molecular dynamics simulations[J]. The Journal of Physical Chemistry C, 2009,114(12):5555-5564.

[5] ROSENBAUM E J, ENGLISH N J, JOHNSON J K, et al. Thermal conductivity of methane hydrate from experiment and molecular simulation[J]. The Journal of Physical Chemistry B, 2007,111(46):13194-13205.

[6] ENGLISH N J. Effect of electrostatics techniques on the estimation of thermal conductivity via equilibrium molecular dynamics simulation: application to methane hydrate[J]. Molecular Physics, 2008,106(15):1887-1898.

[7] ENGLISH N J, JOHN S T. Mechanisms for thermal conduction in methane hydrate[J]. Physical Review Letters, 2009,103(1):015901.

[8] ENGLISH N J, JOHN S T, CAREY D J. Mechanisms for thermal conduction in various polymorphs of methane hydrate[J]. Physical Review B, 2009,80(13):134306.

[9] ENGLISH N J, JOHN S T. Guest and host contributions towards thermal conduction in various polymorphs of methane hydrate[J]. Computational Materials Science, 2010,49(4):S176-S180.

[10] KIRCHNER M T, BOESE R, BILLUPS W E, et al. Gas hydrate single-crystal structure analyses[J]. Journal of the American Chemical Society, 2004,126(30):9407-9412.

[11] ABASCAL J L F, VEGA C. A general purpose model for the condensed phases of water: TIP4P/2005[J]. The Journal of Chemical Physics, 2005,123(23):234505.

[12] JORGENSEN W L, MADURA J D, SWENSON C J. Optimized intermolecular potential functions for liquid hydrocarbons[J]. Journal of the American Chemical Society, 1984,106(22):6638-6646.

[13] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995,117(1):1-19.

[14] NOSE S. A unified formulation of the constant temperature molecular dynamics methods[J]. The Journal of Chemical Physics, 1984,81(1):511-519.

[15] HOOVER W G. Canonical dynamics: equilibrium phase-space distributions[J]. Physical Review A, 1985,31(3):1695.[16] SCHOBER H, ITOH H, KLAPPROTH A, et al. Guest-host coupling and anharmonicity in clathrate hydrates[J]. The European Physical Journal E: Soft Matter and Biological Physics, 2003,12(1):41-49.

[17] ZHANG X, HU M, TANG D. Thermal rectification at silicon/horizontally aligned carbon nanotube interfaces[J]. Journal of Applied Physics, 2013,113(19):194307.

(编辑 沈玉英)

Molecular dynamics simulation and analysis of thermal conductivity of methane hydrate

YANG Dewei1, LIU Yuwen2，XIU Yu3, XU Hongguo2，YUAN Kunpeng1，XU Zhe1

(1.CollegeofPipelineandCivilEngineeringinChinaUniversityofPetroleum，Qingdao266580,China； 2.BinnanOilProductionPlantofShengliOilfieldBranch,SINOPEC，Binzhou256600,China； 3.ProjectConstructionManagementCenterofCityConstructionBureauofHuangdaoDistrictinQingdao,ShandongProvince,Qingdao266555,China)

The heat conduction of methane hydrate was simulated using equilibrium molecular dynamics, and the thermal coupling between methane molecules and water lattices was studied by combining with the analysis of phonon density of states (VDOS). The influence of Van der Waals interaction strength on the temperature dependence of thermal conductivity was also investigated. The results show that the thermal conductivity increases proportionally with the enhancement of the Van der Waals interaction strength. With the increase of the interaction strength, the vibration peak of methane molecules shifts to a higher frequency region because of the stronger vibration coupling and the better matching of VDOS between methane molecules and water lattices, and then the thermal conductivity of methane hydrate is enhanced. The temperature dependence at high temperature may be attributed to inelastic scattering of the phonon caused by the appearance of phonons with the immediate relaxation time, while at low temperature it may be attributed to the confinement of the optic phonon modes and low frequency phonons. The calculated temperature dependence trend agrees well with the experimental results.

methane hydrate; molecular dynamics; phonon; thermal conductivity

2015-06-10

国家自然科学基金项目 (U1262112)

杨德伟(1964-),男,教授,博士,研究方向为热能工程技术。E-mail:yangdw@upc.edu.cn。

1673-5005(2016)04-0141-05

10.3969/j.issn.1673-5005.2016.04.019

TK 124

A

杨德伟，刘雨文，修毓,等.甲烷水合物热导率分子动力学模拟及分析[J]. 中国石油大学学报(自然科学版),2016,40(4):141-145.

YANG Dewei, LIU Yuwen, XIU Yu, et al. Molecular dynamics simulation and analysis of thermal conductivity of methane hydrate[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(4):141-145.