控压钻井井控过程中排量优化设计

何 淼, 柳贡慧,2, 李 军, 熊 超, 游子卫

(1.中国石油大学石油工程学院,北京 102249; 2.北京工业大学,北京 100124;3.新疆油田公司工程技术研究院,新疆克拉玛依 834000; 4.华北油田采油工程研究院,河北任丘 062552)



控压钻井井控过程中排量优化设计

何 淼1, 柳贡慧1,2, 李 军1, 熊 超3, 游子卫4

(1.中国石油大学石油工程学院,北京 102249; 2.北京工业大学,北京 100124;3.新疆油田公司工程技术研究院,新疆克拉玛依 834000; 4.华北油田采油工程研究院,河北任丘 062552)

控压钻井井控是处理气侵溢流问题的有效新方法,包括前期控制和循环排气两个阶段。基于快速施加井口回压控制方法,根据气液固多相流理论,建立控压钻井井控数学模型,并采用有限差分法迭代求解。在此基础上,分析排量对最大井口回压、最大套管鞋处压力和最大立管压力的影响,并提出基于井控安全目标函数的排量优化设计方法。模拟结果表明:在循环排气阶段,立管压力维持不变且为最大值,井口回压达到最大值与气体前沿运移到井口之间存在明显的时间滞后性,气体运移到套管鞋处时套管鞋处压力最大;验证了以出入口流量一致表征井底气侵停止的合理性。模型计算得到的压力值与实验测量值吻合较好。

控压钻井; 井控; 井口回压; 循环排气; 井控安全; 排量优化

目前在油气资源勘探开发过程中,复杂地层钻井比例不断加大,由于气侵溢流引起的井控安全问题日益突出。控压钻井(managed pressure drilling, MPD)井控是解决该类问题的有效新手段,包括前期气侵控制和循环排气阶段,较常规井控方法(司钻法/工程师法),其借助旋转控制头、节流管汇和科里奥利质量流量计等井口装备,可以在不关井的条件下快速处理溢流,成功避免了由关井作业可能引起的压漏地层和开关泵时压力波动等问题[1],大大减少了非生产作业时间,并提高了钻井安全性。Das[2]、Guner[3]、Davoudi[4]和Smith[5]分别针对控压钻井井控过程中前期控制方法进行了相关研究,主要分析了快速增加井口回压、增加循环排量、MPD式动态关井和常规关井4类前期气侵控制方法的适用性,指出快速增加井口回压是一种较理想的方法,并确定了出入口流量一致为井底气侵停止的标志,同时建议在循环排气阶段采用原钻井液排量。但是现有研究仅限于前期控制方法,并未对循环排气阶段中的参数变化特性进行分析,可能无法保证井控安全。笔者建立控压钻井井控模型,定量描述井控全过程的相关参数变化规律,并提出基于井控安全目标函数的排量优化设计方法。

1 控压钻井井控全过程

针对控压钻井工艺特性,将控压钻井井控全过程具体分为3个阶段:阶段1,地面未监测到溢流时井底气体持续侵入阶段,在该阶段随着钻进中打开储层厚度的延长,气侵量快速增加;阶段2,地面监测到溢流后,为避免继续打开储层停止钻进作业,迅速调节节流阀以施加井口回压,当出入口流量近似相同时,确认井底气侵停止,快速施加井口回压阶段结束,在该阶段钻井液排量维持不变;阶段3,为保持井底恒压,基于立压控制法采用一定的钻井液排量循环排气阶段,该阶段包括气体运移至井口和气体排出井筒阶段。根据井控过程中井筒流体分布随时间变化关系,同时由于快速施加井口回压阶段非常短暂,可以忽略此阶段停钻对岩屑产生速度的影响,将控压钻井井控全过程简化为(a)、(b)、(c)类物理模型(图1)。阶段1和阶段2统一表征为(a)类物理模型,此时井筒内存在两个区域,上部为钻井液、岩屑液固两相流区域,下部为气、液、固三相流区域。阶段3中的气体运移阶段表征为(b)类物理模型,由于成功控制住井底溢流,井筒内存在3个区域,上部为液固两相流区域,中部为气、液、固三相流区域,而下部为纯液相的单相流区域。阶段3中的气体排出井筒阶段表征为(c)类物理模型,此时井筒内有着气、液、固三相流和纯液相两个区域,且随着时间的推移,单相流段不断延长。

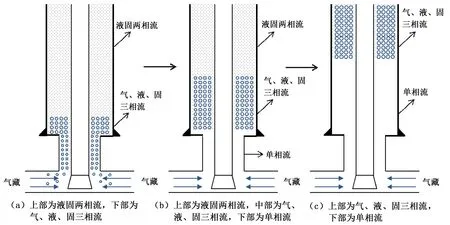
图1 控压钻井井控全过程示意图Fig.1 Schematic diagram of whole process of MPD well control

主要针对阶段3(循环排气阶段)的钻井液排量进行优化设计。控压钻井井控过程须满足:①允许的最大井口回压必须严格控制在旋转控制头额定工作压力之内;②避免套管鞋处薄弱地层破裂;③最大立管压力不超过泥浆泵额定作业压力。

2 控压钻井井控数学模型

为建立控压钻井井控数学模型,假设:井筒流体做一维轴向流动,忽略径向变化,流体温度按线性梯度计算;钻井液为赫巴流体,且不可压缩;不考虑气体溶解的影响,忽略气、液、固相间质量传递。

2.1 气、液、固多相流控制方程

气相质量守恒方程为

(1)

液相质量守恒方程为

(2)

固相质量守恒方程为

(3)

气、液、固三相动量守恒方程为

(4)

式中,A为环空流道面积,m2;ρg、ρl和ρs分别为气相、钻井液和岩屑的密度,kg/m3;αg、αl和αs分别为气相、钻井液和岩屑的体积分数;vg、vl和vs分别为气相、钻井液和岩屑的实际流速,m/s;qg为单位厚度气体侵入速度,kg/(s·m);qs为单位厚度岩屑产生速度,kg/(s·m);g为重力加速度,取9.81 m/s2;θ为井眼方向与水平方向的夹角;pf为沿程压耗,Pa。

2.2 压耗模型

沿程压耗pf仅包括摩阻压降和加速度压降两部分,则井筒内流体沿程压耗的统一表达式为

(5)

其中

ρm=ρgαg+ρlαl+ρsαs,vm=vsg+vsl+vss.

式中,f为范宁摩阻系数;ρm为气、液、固混合物密度,kg/m3;vm为气、液、固混合物速度,m/s;D为当量直径,m;pac为加速度压降,Pa;vsg、vsl和vss分别为气相、钻井液和岩屑的表观流速,m/s。

根据非牛顿流体的广义流性指数研究方法,将环空和圆管流的压耗计算方法统一,用于计算钻柱内单相流、环空中单相流和液固两相流的范宁摩阻系数f值,同时忽略加速度压降的影响。当广义雷诺数Re≤2 100时,流态为层流,f=16/Re;当广义雷诺数Re>2 100时,流态为紊流,选用考虑粗糙度影响的Reed-Pilehvari[6]公式求取f。

环空多相流压耗计算与流型息息相关,基于前人的研究成果[7-10],将垂直环空管中的流型划分为泡状流、分散泡状流、段塞流、搅动流和环状流。当流型是泡状流、分散泡状流以及环状流时,加速度压降非常小,可以忽略不计。当流型是段塞流和搅动流时,加速度压降不可忽略。文中段塞流采用机理模型[11]计算,根据泰勒气泡长度的发展变化,段塞流分为发达的和发展中的段塞流,同时搅动流中的气液相分布与段塞流类似,因此选用段塞流模型计算搅动流压耗。多相流流态不分层流或紊流,f值一概选用Colebrook[12]公式求取。

2.3 漂移流模型

针对气液两相流复杂的流动问题,Zuber和Findlay[13]提出了考虑气液相间滑脱效应的漂移流模型,比均相流和分流模型更加符合实际流动规律,计算误差更低。岩屑颗粒在环空内钻井液中运动因重力差有着相对运动速度,因此岩屑运移同样可用漂移流模型描述。从漂移流定义出发,环空中气相和固相的实际流速为

vg=c0vm+vgr,

(6)

vs=c1vef-vsr.

(7)

式中,c0为气相分布系数;vgr为气相滑脱速度,m/s;c1为固相分布系数;vef为有效返速,m/s;vsr为固相沉降速度,m/s。

在固相漂移流模型中,当流型为泡状流或分散泡状流时,有效返速vef=vm,当流型为段塞流、搅动流或环状流时,泰勒气泡或气芯中的气体流速达不到携岩要求,此时有效返速vef=vsl。Iyoho[14]推荐c1取1。参考Chien[15]总结的不规则岩屑颗粒的阻力系数表达式和环空中岩屑受力平衡原理,得出忽略颗粒加速过程的沉降速度,即

(8)

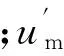
考虑倾斜角和气泡群影响的泡状流中气泡滑脱速度为

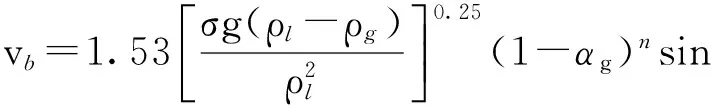
(9)

段塞流或搅动流的泰勒气泡滑脱速度表达式为

(10)

泡状流或段塞流向分散泡状流的转变条件为

(11)

环状流的转变须符合防止液滴回落所需要的最低气速,即

(12)

其中

Dep=Do+Di,Dh=Do-Di.

式中,σ为表面张力,N/m;n为群效应系数,一般取值0.5;Dep为等边缘直径,m;Dh为水力直径,m。

Taitel等[16]指出一旦小气泡的滑脱速度大于泰勒气泡的滑脱速度,小气泡将聚集成大的泰勒气泡而转变成段塞流,因此泡状流存在最小管径。联立式(9)和(10)求出的Dep即是最小管径Dmin。

气相漂移流模型中不同流型的判别条件以及分布系数和滑脱速度选取见表1。

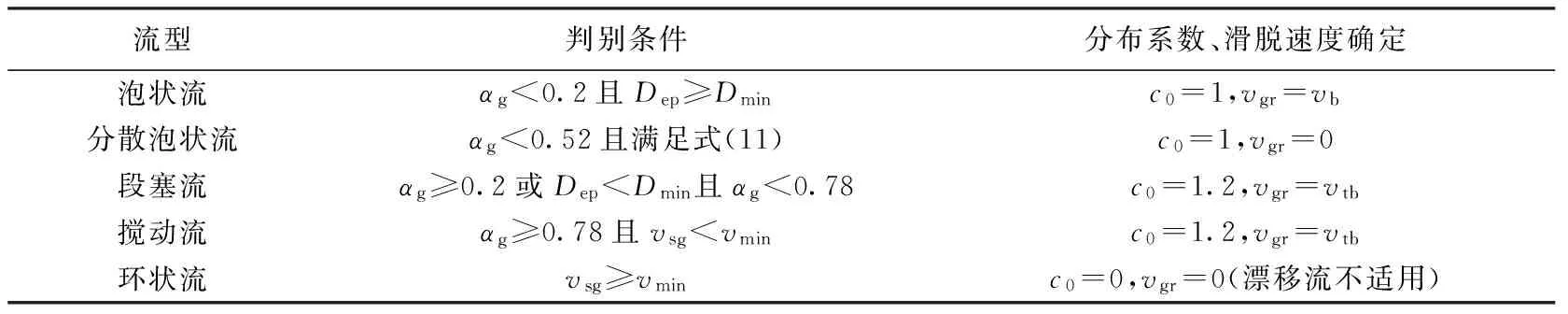
表1 流型判别和漂移流模型的参数选取

2.4 地层渗流模型

在钻遇气藏时,若井底压力小于地层压力,地层气体将侵入井筒环空。气体侵入过程符合非达西渗流,则流入井筒中的气体体积流量可用二项式定理计算,即

(13)

其中

式中,qsc为标准状况(0 ℃,101 325 Pa)气体流量,m3/d;pe为地层压力,MPa;pwf为井底气体流压,MPa;T为储层温度,K;re为气藏供给半径,m;rw为底部井筒半径,m;β为紊流系数;γg为气体的相对密度;h(t)为打开气藏厚度,m;k为地层渗透率,10-3μm2;S为表皮系数。

3 模型求解

针对环空气、液、固多相流瞬态模型,采用气液界面追踪和有限差分法迭代求解[17],其中关于控制方程的显式差分处理:一阶空间导数采用一阶迎风格式,一阶时间导数采用4点中心差分格式。以此原则将控制方程离散化,给出相应的有限差分格式。

气相:

(14)

液相:

(15)

固相:

(16)

动量守恒方程为

(17)

其中

k=Aj-1/Aj,TS1=ρgαgvg+ρlαlvl+ρsαsvs,

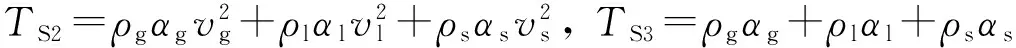
4 模型验证

利用Tulsa大学的大尺寸试验井筒数据[18]进行多相流模型验证。倾斜井筒长27.43 m,与垂直方向夹角15°,井筒内径203.2 mm,钻杆外径114.3 mm,钻柱允许以0～150 r/min的速度旋转,气相介质选用空气,液相介质有清水和聚合物水溶液两类。聚合物水溶液的钻井液性能为:密度1 011 kg/m3,动切力1.91 Pa,塑性黏度11 mPa·s。同时分别在距井筒中心11.58 m的两端装有传感器,以此测量23.16 m高度的总压降。Sunthankar[19]由测量结果得出钻柱旋转对于井筒压力的影响非常小,因而采用钻柱不旋转、液相介质为具有非牛顿特性的聚合物水溶液条件下的压降测量值。

将不同液相表观速度下的测量结果与模型计算值进行对比,如图2所示。由图2可知,模拟值与实测值的变化规律基本一致:随着气相表观速度的增加,总压降逐渐降低,并且当气相表观速度一定时,液相表观速度较大的一方总压降值更大。图3为绝对误差分布。可以看出,随着气相表观速度的增加,绝对误差基本呈上升趋势。当表观液相速度分别为0.50和0.71 m/s时,平均绝对误差仅为4.17%和3.22%,表明本文模型的计算结果与测量数据吻合较好,拥有较高的精度,验证了模型的可靠性。

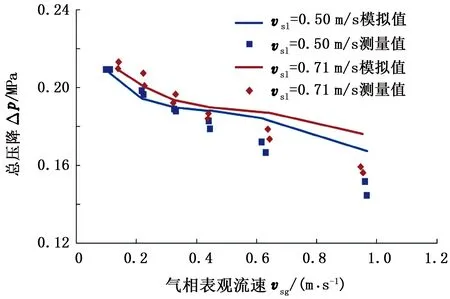
图2 试验测量数据与模拟计算值对比Fig.2 Comparison of experimental measuring results and simulated results

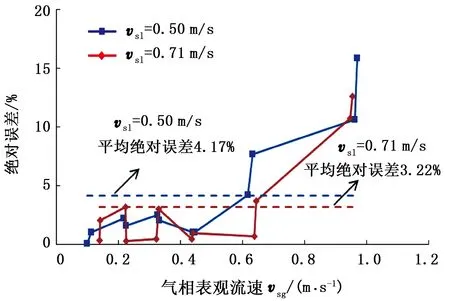
图3 绝对误差分布Fig.3 Absolute error distribution

5 数值模拟

以塔中北部某口直预探井为例开展数值模拟研究,约束参数上限:①参考Hamoudi[19]推荐的RCD额定工作压力6.14 MPa;②套管鞋处薄弱地层破裂压力当量密度为2.0 g/cm3;③现场采用FC 1600型泥浆泵,额定泵压35 MPa。其余基础数据如下:井深5 000 m,上层套管下深3 200 m,钻头直径215.9 mm,钻杆外径127 mm,钻杆内径108.6 mm,喷嘴面积721 mm,循环排量22 L/s,钻井液密度1 650 kg/m3,塑性黏度28 mPa·s,稠度系数0.21 Pa·sn,流性指数0.74,动切力2.85 Pa,地表温度21.3 ℃,地温梯度0.02 ℃/m,气藏渗透率20×10-3μm2,气藏供给半径150 m,气体相对密度0.62,表皮系数2,地层压力73 MPa,初始井口回压1.4 MPa,液面预警值0.636 m3,机械钻速3.67 m/h,岩屑颗粒直径5 mm,颗粒球形度0.792 4。

5.1 气侵停止前参数变化特征

图4为气侵停止之前即(阶段1+阶段2)的泥浆池增量和气侵速度随时间变化曲线。由图4可知,“0”时刻是井底气侵开始点,此时钻头恰好至气藏顶部。此后随着时间的推移,钻进引起的打开气藏厚度不断延长,导致气侵速度逐渐增加,泥浆池液面也随之上涨。t=16.3 min,为地面监测溢流时间,此时泥浆池增量增至预警值0.636 m3。在随后的快速增加井口回压阶段(16.3～18.1 min),气侵速度快速下降至零,同时在1.8 min的控制阶段额外的泥浆池增量仅为0.054 m3。

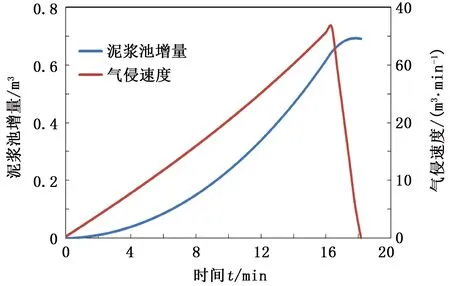
图4 泥浆池增量、气侵速度随时间变化Fig.4 Variation of pit gain and gas kick rate with elapsed time

图5为气侵停止前出口流量和井底压力随时间变化曲线。随着时间的推移,出口流量逐渐增加,直至地面监测溢流时间后,由快速施加井口回压引起出口流量迅速下降。井底压力动态变化规律与出口流量的变化正好相反,呈先降低后升高趋势。在结束点t=18.1 min,出口流量近似等于入口流量,而且此时的井底压力仅高于地层压力0.2 MPa,井底处于微过平衡状态。这也从数值模拟方面证明了出入口流量一致表征井底气侵停止的合理性。

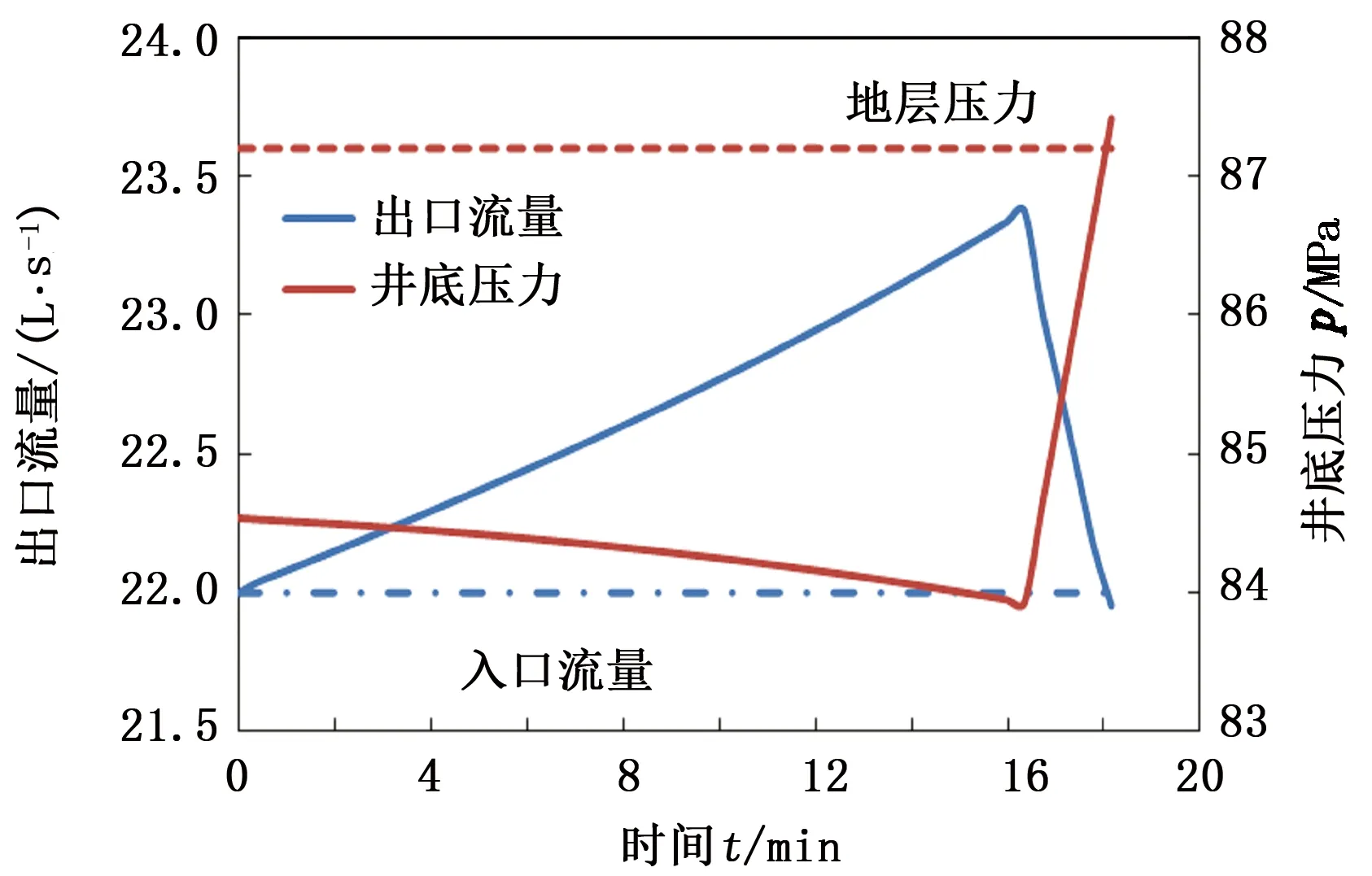
图5 出口流量、井底压力随时间变化Fig.5 Variation of outlet flow and bottomhole pressure with elapsed time

5.2 井控全过程的参数变化特征

图6、7为井控全过程中泥浆池增量、井口回压以及套管鞋处压力、立管压力随时间变化曲线。首先得出控压钻井井控全过程中各阶段的时间分布,气体持续侵入阶段(0～16.3 min),快速施加井口回压阶段(16.3～18.1 min),基于立压控制法循环排气阶段(18.1～94.9 min),其中包括气体运移至井口阶段(18.1～78.2 min)和气体排出井筒阶段(78.2～94.9 min)。

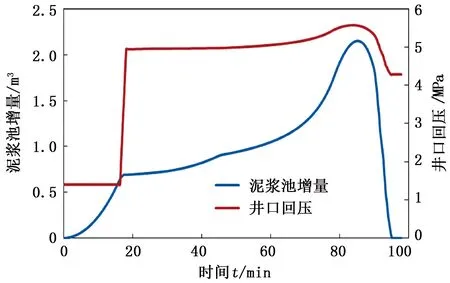
图6 泥浆池增量、井口回压随时间变化Fig.6 Variation of pit gain and wellhead back pressure with elapsed time

由图6可以看出,在快速施加井口回压阶段,井口回压由初始压力值1.4 MPa迅速上升至4.9 MPa。在循环排气阶段,井口回压和泥浆池增量的变化规律基本相同,随着时间的推移,两者均先增加后减小,并且在85.2 min左右同时达到最大值。这是因为在井底压力一定条件下,井口回压是为了补偿气体上升膨胀过程中液柱压力的降低值,因而井口回压和泥浆池增量呈正相关性。该极大值时间点(85.2 min)与气体刚运移至井口时间点(78.2 min)有着明显的时间滞后性,这是因为气侵速度从零值开始逐渐增加,前沿气体的速度和体积分数相对较小,气体刚好抵达井口时,泥浆池增量并未达到最大值,受气体运移膨胀的影响,直至85.2 min,泥浆池增量最大为2.15 m3,同时井口回压达到最大值5.57 MPa。

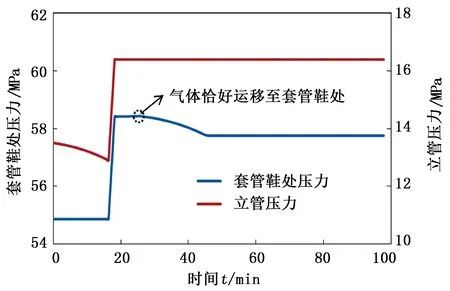
图7 套管鞋压力、立管压力随时间变化Fig.7 Variation of casing shoe pressure and standpipe pressure with elapsed time

由图7可以看出,随着时间的推移,立管压力先不断降低后快速增加,最终在循环排气过程中保持不变且为最大值。在循环排气阶段,当气体运移至套管鞋处之前,套管鞋处压力随着时间的推移而缓慢增加,以致图中蓝线观察不明显。原因是该阶段基于井底恒压原则,在气体运移至套管鞋处之前,此处压力相应补偿气体膨胀效应,同时在套管鞋3 200 m以下,气体膨胀并不明显,因而套管鞋处压力缓慢增加。前沿气体运移到套管鞋处以后的过程可以近似看作套管鞋至井底井段的气体排出过程,套管鞋处压力逐渐降低,最终气体全部排出后,该处压力恢复平衡，因此气体恰好运移至套管鞋处时,套管鞋处压力达到最大值。

5.3 约束参数随排量的变化

基于对图6和图7的分析,定量确定了井口回压、套管鞋处压力和立管压力的最大值,在此基础上给出三者随排量变化规律。此外,出于井控安全考虑,RCD额定压力、薄弱地层破裂压力和额定泵压还须选用合适的安全系数(SF)。

井筒压力主要分为静液柱压力和摩阻压力两部分,而摩阻压力与排量直接相关联,这样构建了排量与井筒压力的关系。首先考察纯钻井液条件下排量对环空摩阻的影响(图8)。总的来说,环空摩阻随着排量的增加而增大。但是针对不同的钻井液流态,摩阻变化存在着差异。相比层流,环空内完全紊流时的摩阻压力随排量的增加速率相对较快。同时由于裸眼井段环空截面积较小,当裸眼井段达到紊流时,上层套管环空可能仍然处于层流。当排量为28～34 L/s时,环空内为局部紊流状态,此时摩阻压力变化小幅波动。

由图8(b)可以看出,随着排量的增加,最大井口回压逐渐降低。最大井口回压变化受环空流态影响明显,完全紊流时的最大井口回压随排量变化速率较层流加快,同样在局部紊流区域存在小幅波动现象。取安全系数SF=1.2,校正后的RCD额定压力为5.11 MPa。如果按照原钻井液排量(22 L/s)进行循环排气,则最大井口回压为5.57 MPa,显然高于RCD额定压力,导致井口装备失效。这也进一步表明控压钻井井控过程中进行排量优化的必要性。

图8(c)中取安全系数SF=1.05,校正后的薄弱地层破裂压力为59.73 MPa。在原钻井液排量条件下,最大套管鞋处压力为58.4 MPa,低于地层破裂压力,因此不存在地层破裂的风险。随着排量的增加,最大套管鞋处压力逐渐降低,该压力与破裂压力的差值也随之变大。

图8(d)中取安全系数SF=1.1,校正后的额定泵压为31.82 MPa。最大立管压力随着排量的增加而增大,直至排量达到44.3 L/s,最大立管压力等于额定泵压。

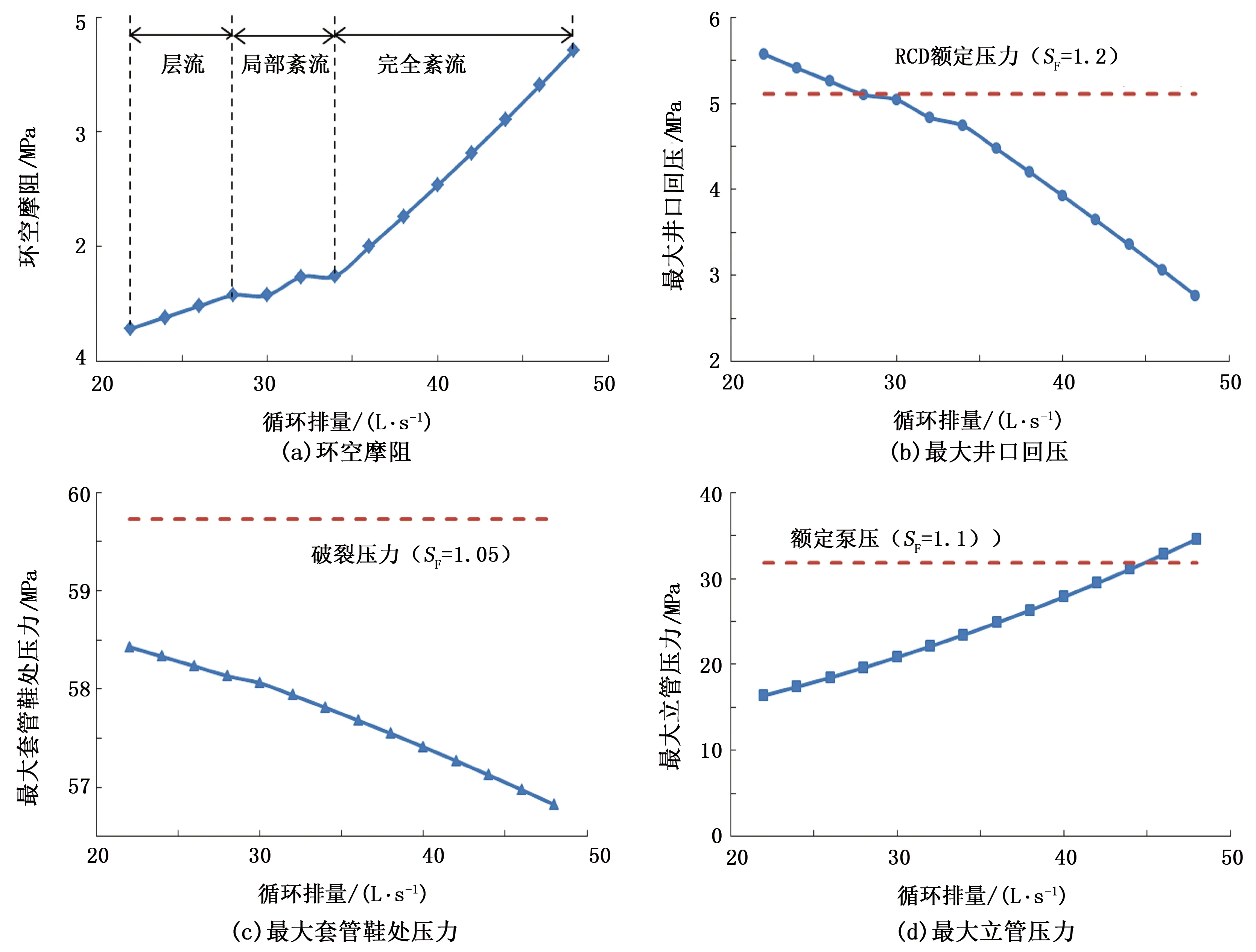
图8 环空摩阻、最大井口回压、最大套管鞋处压力和最大立管压力随排量变化Fig.8 Variation of annular friction, the maximum wellhead back pressure, the maximum casing shoe pressure and the maximum standpipe pressure with pumping rate

6 排量优化设计方法

利用建立的控压钻井井控模型,结合现场控压钻井井控作业方案,提出排量优化设计方法,具体步骤如下:

(1)根据科里奥利流量计记录的出口流量动态曲线,确定气侵“0”时刻,并记录此时的立管压力ps0,根据钻柱内单相流水力计算,得到井底压力pb0。

(2)地面监测到溢流后,通过调节井口节流阀快速施加井口回压,一旦出口流量近似等于入口流量,记录此时的立管压力ps,由于排量不变,确定“0”时刻的井底压差p=ps-ps0,进而得到地层压力pp=pb0+p。

(3)参考邻井地层参数,利用建立的井控模型,作出最大井口回压、最大套管鞋处压力和最大立管压力随排量变化曲线。结合安全系数校核后的RCD额定压力,薄弱地层破裂压力和额定泵压,分别确定约束参数与上限的排量交点Q1、Q2和Q3。原钻井液排量Q0为最小值,如果约束参数与上限值不相交,则交点取值Q0。

(4)确定优化排量Q范围:max[Q1,Q2]≤Q≤Q3。如果max[Q1,Q2]≤Q3,则排量取与原钻井液排量Q0的相近值,即Q=max[Q1,Q2]。反之如果max[Q1,Q2]>Q3,则说明不论怎样调节排量,均不能保障井控安全,只能选择常规井控作业。

参考本文算例,利用提出的排量优化设计方法优选井控过程中的循环排量。分别根据图9、10和11的变化曲线,确定Q1=27.9 L/s,Q2=22 L/s,Q3=44.3 L/s。由于max[Q1,Q2]≤Q3,因此优化排量Q=max[Q1,Q2],即27.9 L/s。这说明当循环排气过程中的排量取27.9 L/s时,可以满足现场井控作业需要。

7 结 论

(1)在快速施加井口回压阶段,当出口流量降至入口流量附近,井底压力恰好高于地层压力,确定了以出入口流量一致表征井底气侵停止的可行性。

(2)在循环排气阶段,井口回压达到最大值与气体前沿运移到井口存在明显的时间滞后性,气体运移到套管鞋处时套管鞋处压力最大,而立管压力维持不变且为最大值。

(3)随着排量的增加,最大井口回压和最大套管鞋处压力逐渐降低,而最大立管压力逐渐增加。基于以上约束参数的承压能力,提出了井控过程中排量优化设计方案,对现场溢流控制和保障井控安全具有积极的意义。

[1]KINIKK,GUMUSF,OSAYANDEN.Acasestudy:firstfieldapplicationoffullyautomatedkickdetectionandcontrolbyMPDsysteminwesterncanada[R].SPE168948, 2014.

[2] DAS A K, SMITH J R, FRINK P J. Simulations comparing different initial responses to kicks taken during managed pressure drilling [R]. SPE 112761, 2008.

[3] GUNER H. Simulation study of emerging well control methods for influxes caused by bottomhole pressure fluctuations during managed pressure drilling [D]. Baton Rouge: Louisiana State University, 2009.

[4] DAVOUDI M, SMITH J R, PATEL B M, et al. Evaluation of alternative initial responses to kicks taken during managed pressure drilling [R]. SPE 128424, 2010.

[5] SMITH J R, PATEL B M. A proposed method for planning the best initial response to kicks taken during managed-pressure-drilling operations [J]. SPE Drilling and Completion, 2012,27(2):194-203.

[6] REED T D, PILEHVARI A A. A new model for laminar, tansitional, and turbulent flow of drilling muds [R]. SPE 25456, 1993.

[7] CAETANO E F. Upward two-phase flow through an annulus [D]. Oklahoma: The University of Tulsa, 1985.

[8] HASAN A R, KABIR C S. Study of multiphase flow behavior in vertical wells [J]. SPE Production Engineering, 1988,3(2):263-272.

[9] ANSARI A M, SYLVESTER N D, SHOHAM O, et al. A comprehensive mechanistic model for upward two-phase flow in wellbores [R]. SPE 20630, 1990.

[10] LAGE A C V M, TIME R W. Mechanistic model for upward tow-phase flow in annuli [R]. SPE 63127, 2000.

[11] PEREZ-TELLEZ C, SMITH J R, EDWARDS J K. A new comprehensive, mechanistic model for underbalanced drilling improves wellbore pressure predictions [J]. SPE Drilling and Completion, 2003,18(3):199-208.[12] COLEBROOK C F, WHITE C M. Experiments with fluid friction in roughened pipes [J]. Proceedings of the Royal Society:Ser A, 1937,161(906):367-381.

[13] ZUBER N, FINDLAY J A. Average volumetric concentration in two-phase flow systems [J]. Journal of Heat Transfer, 1965,87(4):453-468.

[14] IYOHO A W, HORETH J M, VEENKANT R L. A computer model for hole-cleaning analysis [J]. Journal of Petroleum Technology, 1988,20(9):1183-1192.[15] CHIEN S F. Settling velocity of irregularly shaped particles [J]. SPE Drilling & Completion, 1994,9(4):281-289.[16] TAITEL Y, BARNEA D, DUCKLER A E. Modeling flow pattern transitions for steady upward gas-liquid flow in vertical tubes [J]. AIChE Journal, 1980,26(3):345-354.

[17] HE Miao, LIU Gonghui, LI Jun, et al. A study of rapid increasing choke pressure method for sour gas kicks during managed pressure drilling [J]. International Journal of Oil, Gas and Coal Technology, 2016,11(1):39-62.

[18] SUNTHANKAR A A, KURU E, MISKA S, et al. New developments in aerated mud hydraulics for drilling in inclined wells [J]. SPE Drilling & Completion, 2003,18(2):152-158.

[19] HAMOUDI B, KARTOBI K, QUTOB H, et al. Conventionally undrillable open fractured reservior, successfully drilled using managed pressure drilling technology in Algeria [R]. SPE 138579, 2010.

(编辑 李志芬)

Optimization of pumping rate for well control during managed pressure drilling

HE Miao1, LIU Gonghui1,2, LI Jun1, XIONG Chao3, YOU Ziwei4

(1.CollegeofPetroleumEngineeringinChinaUniversityofPetroleum,Beijing102249,China; 2.BeijingUniversityofTechnology,Beijing100124,China; 3.ResearchInstituteofEngineeringTechnologyofXinjiangOilfield,Karamay834000,China; 4.ResearchInstituteofPetroleumProductionEngineeringofHuabeiOilfield,Renqiu062552,China)

Well control via managed pressure drilling (MPD) is a new and effective method to deal with gas kicks and overflow problems, which includes two stages: initial control response and circulating out of gases. According to the gas-liquid-solid multiphase flow theory, a MPD well control model based on rapidly applying wellhead back pressure method was established, and a finite difference method was used to iteratively solve the model. The effects of pumping rate on the maximum wellhead back pressure, maximum casing shoe pressure and maximum standpipe pressure were analyzed using the model, and an optimized design method for the pumping rate as the objective function for well control safety was proposed. The simulation results show that, in the stage of gas circulating out, the standpipe pressure remains unchanged with its maximum value, and the peak value of the wellhead back pressure appears before the gas front migrates to the wellhead, while the maximum value of the casing shoe pressure appears when the gas front migrates to the casing shoe. The reasonability of using the consistence of outlet flow and inlet flow to indicate the stoppage of bottom hole influx can be verified using the model. The calculated pressure values using the model agree well with the experimental results.

managed pressure drilling; well control; wellhead back pressure; circulating out of gas; well control safety; pumping rate optimization

2015-09-10

国家自然科学基金项目(51334003，51274221，51274045，51374223)

何淼(1989-)，男，博士研究生，研究方向为控压钻井、欠平衡钻井和井筒多相流计算。E-mail：18810459934@163.com。

1673-5005(2016)04-0096-08

10.3969/j.issn.1673-5005.2016.04.012

TE 242

A

何淼，柳贡慧，李军，等. 控压钻井井控过程中排量优化设计[J].中国石油大学学报(自然科学版)，2016,40(4)：96-103.

HE Miao, LIU Gonghui, LI Jun, et al. Optimization of pumping rate for well control during managed pressure drilling[J].Journal of China University of Petroleum(Edition of Natural Science)，2016,40(4)：96-103.