星状集输管网拓扑结构的整体优化

刘 刚, 许继凯, 国志刚, 陈 雷, 卢兴国, 滕厚兴, 徐睿妤

(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.山东省天然气管道有限责任公司，山东济南 250101;3.中国石化胜利油田分公司油气集输总厂,山东东营 257000)



星状集输管网拓扑结构的整体优化

刘 刚1, 许继凯2, 国志刚3, 陈 雷1, 卢兴国1, 滕厚兴1, 徐睿妤1

(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.山东省天然气管道有限责任公司，山东济南 250101;3.中国石化胜利油田分公司油气集输总厂,山东东营 257000)

针对星状集输管网结构特点,建立以管网建设总投资为目标函数,以系统中节点连接关系、站点位置、管线参数为优化变量的星状油气集输管网拓扑结构优化模型。将蚁群算法与遗传算法相结合对模型进行整体优化求解。在蚁群算法中,将节点连接关系的确定转化为路径选择问题,将启发因子表示为管段建设成本的函数,用路径方案对应的管网建设总成本计算信息素的积累量。在遗传算法中,以格雷码形式将站址信息储存于染色体上,用蚁群算法求得每种站址分布方案下最优井组和管径,并用其计算各染色体的适应度,从而同步求得最佳站址、最佳井组划分和管线参数。结果表明,所设计算法优化质量高于分级优化,且鲁棒性强,不受计算初始值影响。

集输管网; 拓扑结构; 分步优化; 整体优化; 蚁群算法; 遗传算法

集输管网是油田地面工程中的重要组成部分,负责连接井场、计量站、接转站、联合站等集输站点,并将井口产物输送至各站点进行计量、净化、稳定和外输[1]。对集输管网进行拓扑结构优化可以有效减小管线长度,合理分布集输站点,降低集输管网建设投资。由于管网拓扑结构优化问题往往同时涉及到离散变量和连续变量,当系统内的井场和集输站点数量到达一定规模后,将无法对原问题进行直接精确地求解[2-3]。针对现有星状集输管网拓扑结构优化模型中经济因素考虑不足、分步优化策略难以寻得全局最优解的问题,笔者建立体现管线和集输站点建设经济性的优化模型,编制遗传算法嵌套蚁群算法的整体优化算法,并对某油田管网布局和管线参数进行同步计算,验证模型和求解方法的可靠性。

1 概 述

目前,星状集输管网的拓扑结构优化一般采用分步优化的方式求解,即将原问题分为井组划分和站址优化等若干子问题。井组划分确定井站间的最优隶属关系;站址优化确定计量站、联合站等集输站点的最佳位置。通过子问题相互迭代可以得到目标函数值的一个单调下降序列[4],一定次数迭代之后即可求得管网整体拓扑结构。于达[5]以各级井、站之间的加权距离和最短作为目标函数,将管网布局分解成油区剖分和优选站址两个步骤。油区剖分即为井组划分过程。刘扬等[6]同样以管网加权距离和最小为目标函数对多级星式网络进行拓扑优化设计,用降维规划法求解井组划分,用求解非线性方程组的方法计算最优站址,但当系统中节点数量较多时,基于贪心思想的求解策略无法保证分组结果的最优性。韩建增等[7]以管线长度最短为目标函数对井组进行划分,并将其转化为标准的指派问题,用匈牙利法进行求解;计量站站址则使用单纯型法优化得到。罗叶新等[8]将集输系统布局优化分为井组划分、站址优化、干支管线布局、管径优化四个步骤,每个步骤根据待解决的问题不同选用不同的目标函数,但文中未给出各步骤中模型的求解方法。

随着群体智能优化算法的不断发展,越来越多的学者将遗传算法、微粒群算法等具有全局寻优能力的算法应用到集输管网拓扑结构优化问题中。Onwunalu等[9]针对大型油气田井场数量众多、搜索空间巨大的特点,定义了井组模式(WPD)并将其作为优化计算的基本单元,从而降低优化对象的数量,并使用微粒群算法优化井组模式的类型和几何结构。刘扬等[10]将星状集输管网的布局问题分为布局层和分配层两个层次,在布局层用遗传算法优化各级站点的几何位置,在分配层用拉格朗日松弛法求解井组划分;杨建军等[11]以管线投资最小建立了拓扑优化数学模型,用基于整数编码的混合遗传模拟退火算法优化井场分组,采用变尺度法优化计量站的最佳站址。虽然二者对遗传算法的应用和改进取得了良好的优化效果,但仍存在一定的问题,如优化目标函数中未考虑集输管网的建设费用,不能保证管网结构的经济最优性;变尺度法等数值计算方法受迭代初值的影响,求目标函数的梯度时易出现不稳定性。李自力等[12]对气田集输管网的站址和管径进行了同步优化,在一定程度上可以降低分步优化对最终优化质量的影响,但该计算需要在确定井组划分关系的基础上进行,并非真正意义上的整体优化。黎斌等[13]提出了基于微粒群算法的井组划分方法,在计算微粒个体的适应值时,直接将井组的产量中心作为集油站站址,存在局限性。冷建成等[14]以集油过程中运距与运量的乘积最小为目标函数建立了管网拓扑优化模型,并采用神经网络算法进行求解,但该算法最终的稳定状态对应局部最小值的可能性较大,易陷入局部最优解。王洪元等[15]在确定集输管网布局的基础上,先用遗传算法得到管线参数的近似最优解,再将其作为蚁群算法的初始值进一步优化,最终得到管径和壁厚的最佳组合。梁潇[16]建立了基于费用最低的油气管道平面线形优化模型,采用遗传算法求解,其对强制性约束和费用性约束的处理有较好的借鉴作用。

2 优化模型

2.1 目标函数

根据油气田开发方案给出的油气井位置坐标和产量等参数,可以初步确定各级集输站点的数量、规模等参数。集输系统拓扑结构中待优化变量主要包括生产节点间连接关系、站点位置和管线参数,结合星状管网的结构特点,以多级布站集输流程为研究对象,将管网建设成本作为目标函数,建立拓扑结构优化模型为

F(U,Δ,D,h)=

(1)

其中

wkji=B0+B1Dkji+B2hkji[17].

式中,U为集输站点位置向量;Δ为井站间或不同级别站点间的连接关系决策向量;D和h为管线参数;N为布站级数;nk为第k级站点的数量;n0为油气井数量;Cji表示第j级中第i个站点建设成本;δkji为第k级中的第j个节点与第k-1级中的第i个节点间的连接关系决策变量;lkji为节点j与节点i之间管线长度;wkji表示节点j与节点i之间管线的单位长度造价,为管径Dkji与壁厚hkji的函数;B0、B1和B2为与管线成本有关的回归系数。

2.2 约束条件

(1)隶属关系约束。

每个低级别站点能且只能与一个高一级别的站点具有连接关系,即

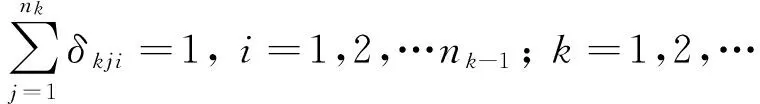
(2)

(2)生产负荷约束。

每个集输站点管辖的次级别站点数量和处理能力应在一定范围内,即

(3)

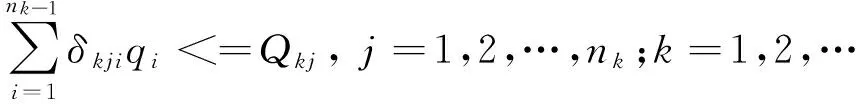
(4)

式中,Mkj为站点j所辖次一级节点数量的最大值;Qkj为站点j的处理能力上限;qi为井场i的产量或站点i的处理量。

(3)回压及进站压力约束。

对于集油过程,井口回压应小于许用值。同时,为了保证计量、分离等工艺的进行,集油管线的进站压力不应小于控制压力,即

pkji≤[pb],

(5)

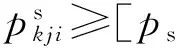
(6)

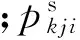
(4)管径约束。

集油管径和壁厚须在一系列标准值中选取。在工程实际中,管径和壁厚的确定与井口回压、产出液流变性质和流量、管线长度等因素有关,虽然现有的部分管网优化研究是以建设投资最低为目标函数,但多未给出管线权因子或投资指标的计算过程。此处利用星状管网井站间管线参数的独立性,通过水力计算优选不同管段的管径和壁厚。

(D,h)⊂ID.

(7)

式中,ID为标准管径集合。

(5)站址约束。

集输站址的选取须在符合生产要求的区域进行,即

U⊂UD.

(8)

式中,UD为站址优化可行域。

3 求解算法设计

3.1 蚁群算法

蚁群算法最早应用于求解TSP问题,对部分经典TSP算例求得了优于其他算法的结果[18]。随后,该算法在给水管网结构和管径优化[19-20]、移动自组网路由确定[21]、长距离输气管道运行参数优化[22]等工程问题中的应用进一步体现了其高效的全局寻优性能。考虑到蚁群算法在求解网络结构问题和路径问题中的独特优势,以及收敛速度慢、易陷入局部最优解等不足[23],采用基于模式学习的小窗口蚁群算法求解井组划分。以包含n口井、m座计量站、1座联合站的二级布站集输管网为例,算法主要步骤如下。

(1)建立模式数组和窗口数组。为了降低数量众多的劣质解对寻优过程的干扰,充分利用蚁群算法在低维空间搜索性能强的优点,预先提取部分优质解存放于模式数组中[24]。为每个计量站建立窗口数组,每只蚂蚁优先从窗口数组与非禁忌元素的交集中选择可行解;若交集为空,则只在非禁忌元素中选择可行解,从而加快算法的收敛速度。

(2)启发函数定义。启发函数θij代表了蚂蚁寻优时路径上的先验性和确定性因素,是蚂蚁从计量站进行状态转移时对各井场的可见度的衡量。将节点间的启发式信息定义为管段建设成本的倒数,表示为

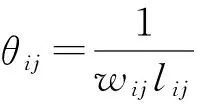
(9)

对于每个计量站,低成本的管段对应的井场均具有相对较大的被选择概率。

此处需要根据给定的站址分布方案,以及回压许用值、管段长度等约束条件,在管径系列中优选出各井到每一座计量站的最佳管线参数,进而得到所有的管段成本,并存于m×n的成本数据表中。当井站间距超过集输半径时,直接将该管段赋以高成本。

(3)状态转移。每只蚂蚁在不同节点间不断移动,从当前节点i到下一节点j的状态转移概率是连接两节点路径上的信息素和启发函数综合作用的结果,第k只蚂蚁在t时刻的状态转移概率计算过程为

(10)

式中,τij和θij分别表示两节点间路径上的信息素量和启发函数;α和β分别为信息素和启发函数的重要程度因子;ak为第k只蚂蚁在当前时刻的允许访问节点集合。

蚂蚁每一次完成转移之后,将被访问节点列为禁忌元素,并对各站点的窗口数组和全局可行解空间进行更新。在蚂蚁的状态转移过程中,通过限制每只蚂蚁从高级别站点出发的次数来满足井式约束。每次转移前验证当前节点是否满足处理量约束:若满足,则视为有效转移;若不满足,则放弃本次转移;从而避免井组划分时出现不可行解。

(4)信息素更新。路径上的信息素的变化包括新信息的积累和已有信息的挥发两个过程,使寻优过程既能充分利用已搜索到的路径信息,又能为新路径的产生提供机会。所有蚂蚁完成一次循环后信息素的挥发和积累计算式为

τij(t+1)=(1-ρ)τij(t)+Δτij(t),

(11)

其中

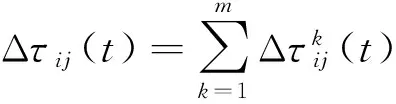
式中,ρ为信息素挥发系数;Δτij(t)为在时刻t的循环中从节点i到节点j路径上的信息素增量,其值与包含该段路径的解的质量正相关,是所有蚂蚁个体综合作用的累加。

为充分利用每个可行解的整体信息,提高寻优过程的全局收敛性,每只蚂蚁对路径信息素的累加规则按Ant-Circle模型计算[25],表示为

(12)

式中,Q表示信息素强度;Fk表示第k只蚂蚁在本次循环中其可行解对应的目标函数值,即管网建设总成本,由式(1)计算得到。

3.2 遗传算法

遗传算法是一种模仿自然选择和遗传变异等生物进化机制的全局性概率搜索算法。集输站点位置优化属于平面内的选址问题,在此充分利用遗传算法的全局寻优性能,在整个站址分布的可行域内搜索集输站点最佳位置。同样以n口井、m座计量站、1座联合站的二级布站集输管网为例,算法主要实现步骤如下。

(1)初始种群产生。初始站址以随机的方式给定,以降低初始值对全局寻优过程的影响,为提高优化速度,先随机产生若干个种群,再从中选择高质量的个体组成初始种群[26]。为了便于交叉和变异操作,采用二进制编码的方式将站场坐标按一定顺序储存于染色体上,其表达式为

R=(x1,y1,x2,y2,…,xm,ym,xm+1,ym+1).

(13)

式中,(xi,yi)为第i座计量站的站址;(xm+1,ym+1)为联合站站址。

为避免汉明悬崖,增强遗传算法的局部搜索能力,将表示站址的二进制码串转化成格雷码。

(2)适应度函数设计。适应度函数负责控制遗传算法优化过程的发展方向。对每个染色体所包含的站址信息,用蚁群算法求解该分布情况下的最优井组划分和管线参数,进一步得到此管网结构的建设总成本,将其作为该染色体的适应度评价指标。

(3)遗传操作设计。遗传操作是遗传算法的核心部分,包括选择、交叉、变异几个过程。其中,选择操作采用基于轮盘赌法的非线性排名选择[27],在每代染色体种群中选出适应度高的个体作为组成新的种群进行交叉和变异。交叉操作采用均匀交叉和多点交叉相结合的方式,且随着种群的进化,逐步增大均匀交叉的概率。变异操作采用随机方式,即在新种群中随机选择个体和基因码位置,对被选择基因在允许的取值范围内随机变异。为确保每个染色体对应的站址分布方案都是可行解,先将优化可行域的坐标转化从零开始的连续值,初始种群的产生和遗传操作都在可行坐标范围内进行,避免不可行站址方案的产生。

根据上述模型建立及求解思路,使用MATLAB编程实现优化过程,其中遗传算法作为优化计算的主程序,蚁群算法为染色体评估的子程序。整体算法流程如图1所示。

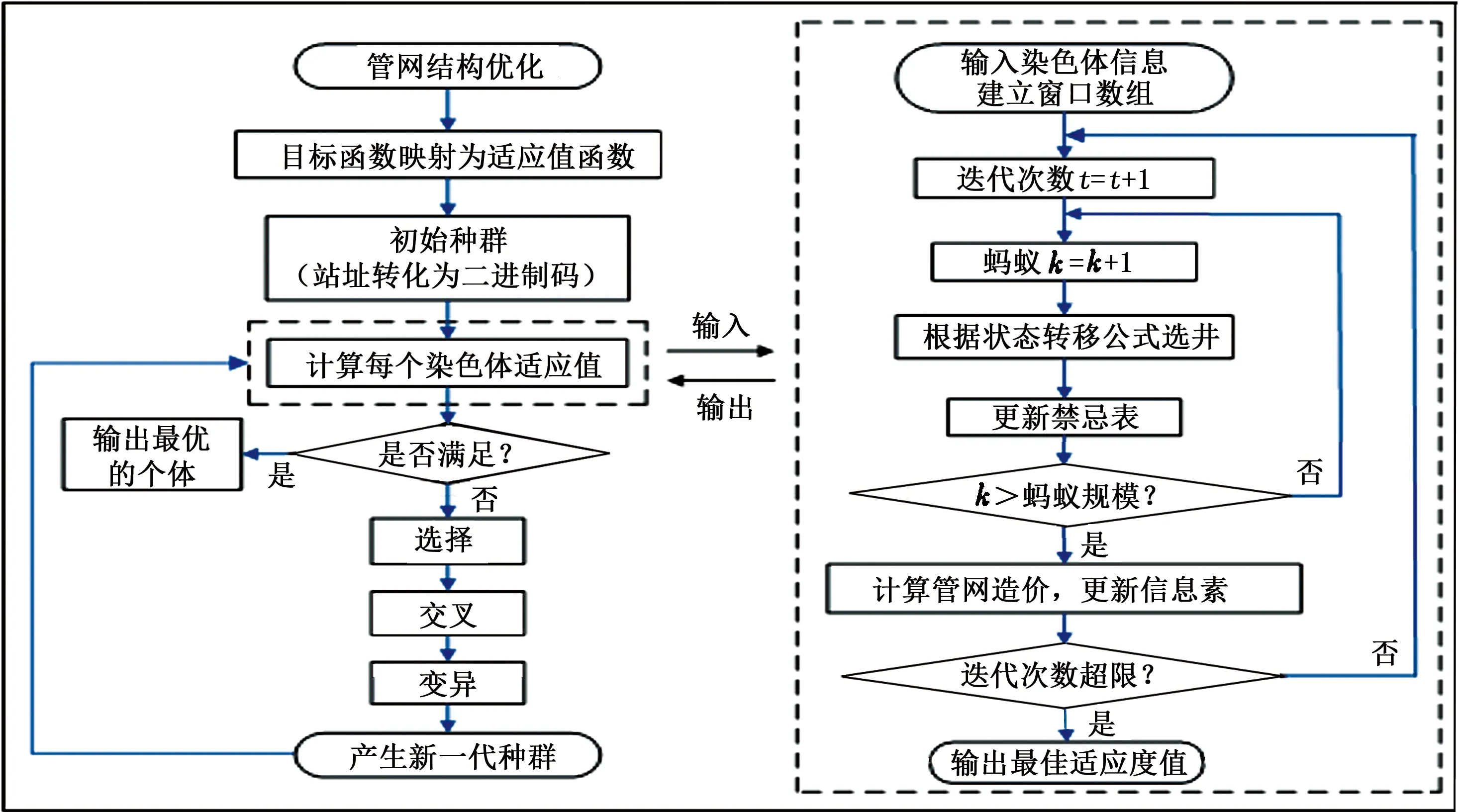
图1 整体优化算法流程图Fig.1 Flow chart of global optimization algorithm

4 算 例

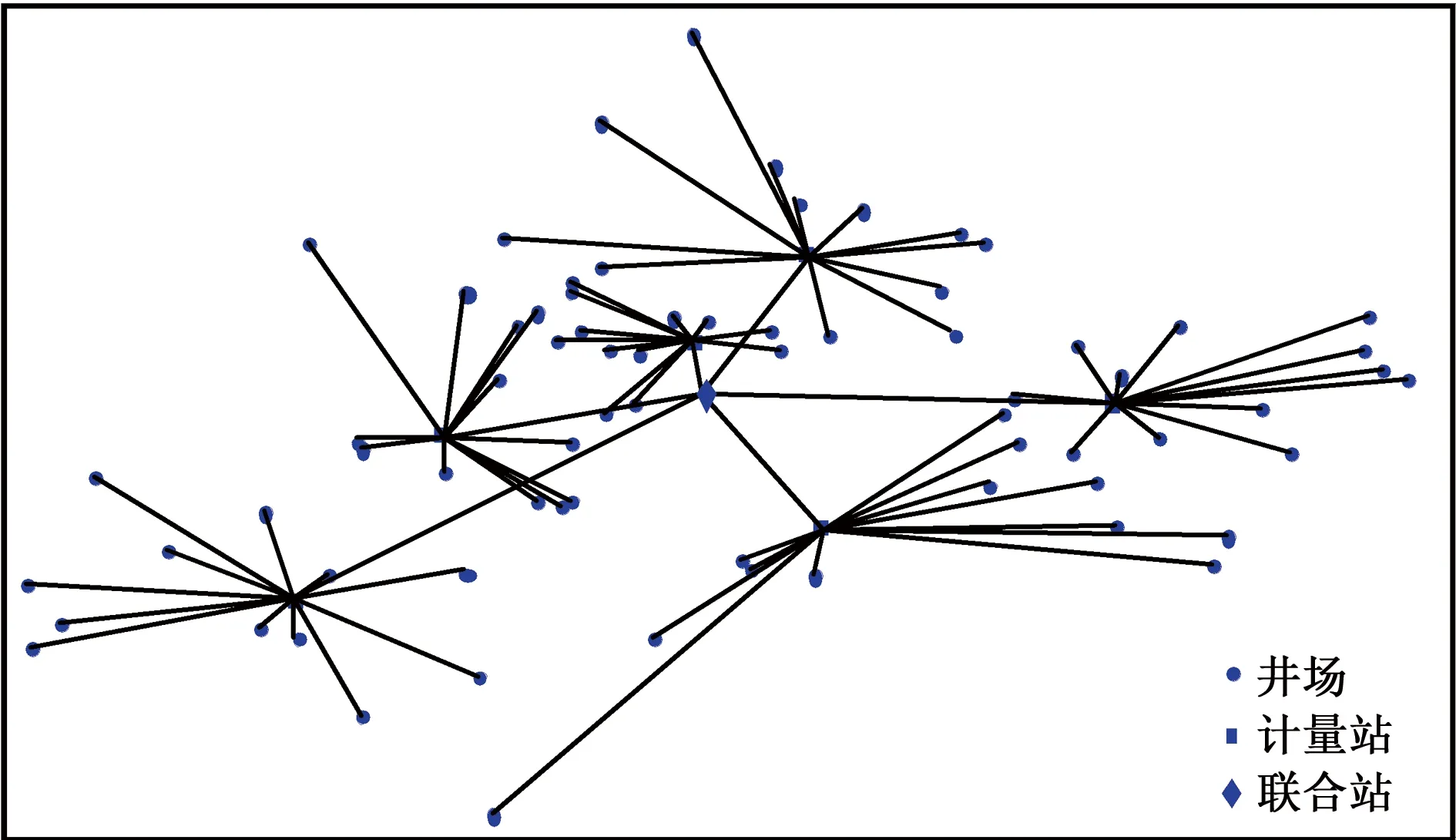
图2 现有集输管网结构连接Fig.2 Present connection of gathering pipeline network structure

以某油田二级布站的星状集输管网为例,建立如式(1)所示的拓扑结构优化模型,分别采用分步优化和整体优化的方法对其进行求解计算。该油田现有油井72口,设计量站6座,集中处理站1座。集输站场数量保持不变,因此目标函数中的站点费用不予计算。井口回压最大许用值为1.2 MPa;计量站的集输半径为1.5 km,最低进站压力为0.7 MPa;联合站最低进站压力为0.4 MPa。管网结构现状如图2所示。井场-计量站管线长度为24.7 km,计量站-联合站管线总长度为3.4 km。在同步优化求解算法中,染色体规模设置为200,进化次数设置为400,变异率设为0.3,交叉率设为0.5。蚁群

规模设为50,循环次数设为70,各计量站的模式数组长度为3,窗口数组根据各站点集输半径范围内井场数量确定,不同站场的窗口数组大小不等。结合该油田提供的材料数据明细,采用式(3)拟合得到不同参数管线的单位长度费用。

图3为采用分步优化和整体优化方法得到的管网连接图。从图3可以看出,分步优化所得的各集输站点站址和分组情况明显优于现有管网结构,采用整体优化方法优化所得管网布局较分步优化结果又有所改进。将优化前、分步优化后、整体优化后管线长度及管网总投资作对比,如表1所示。由表1中数据可知,整体优化算法计算结果的管线总长度为24.0 km,与分步优化结果相比管线长度总和缩短2.3 km;考虑管线参数后,整体优化算法的管网总投资为1 002.9万元,较分步优化结果节省投资91.2万元。对比各管网连接图可以发现:分步优化策略的不足在于给定初值站址之后,后续的井组划分、寻找站址等进一步的迭代优化计算都将在初值的基础上进行,求解范围受初始布局情况的限制,并非在全局空间内搜索最优解;而整体优化算法中,不管是站址优化还是在各种站址分布情况下的井组划分,每一个可行解的求取都是在全局解空间中进行,从而为全局最优解的出现提供可能,避免分步优化时搜索空间受初始值限制的问题。

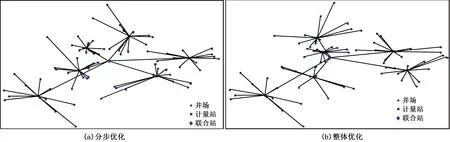
图3 分步和整体优化所得管网连接Fig.3 Pipeline network connection resulting from multilevel optimization and global optimization

步骤井场-计量站管线长度/km投资/万元计量站-联合站管线长度/km投资/万元管线总长/km总投资/万元优化前24.7908.93.4228.428.11137.3分步优化后22.6845.73.7248.426.31094.1整体优化后20.5766.83.5236.124.01002.9

图4为某次染色体评估时各代蚂蚁群体所得井组划分结果随进化次数的变化趋势(各代蚂蚁种群最佳函数值与平均函数值对比),从图4可以看出,井站间管线总造价不断向优化方向发展,说明基于模式学习的小窗口蚁群算法在求解井组划分时全局搜索性能和收敛性能良好,每次可在50代以内得到稳定解。图5为遗传算法中函数值随种群进化次数的变化情况(各代染色体最佳函数值与平均函数值对比)。

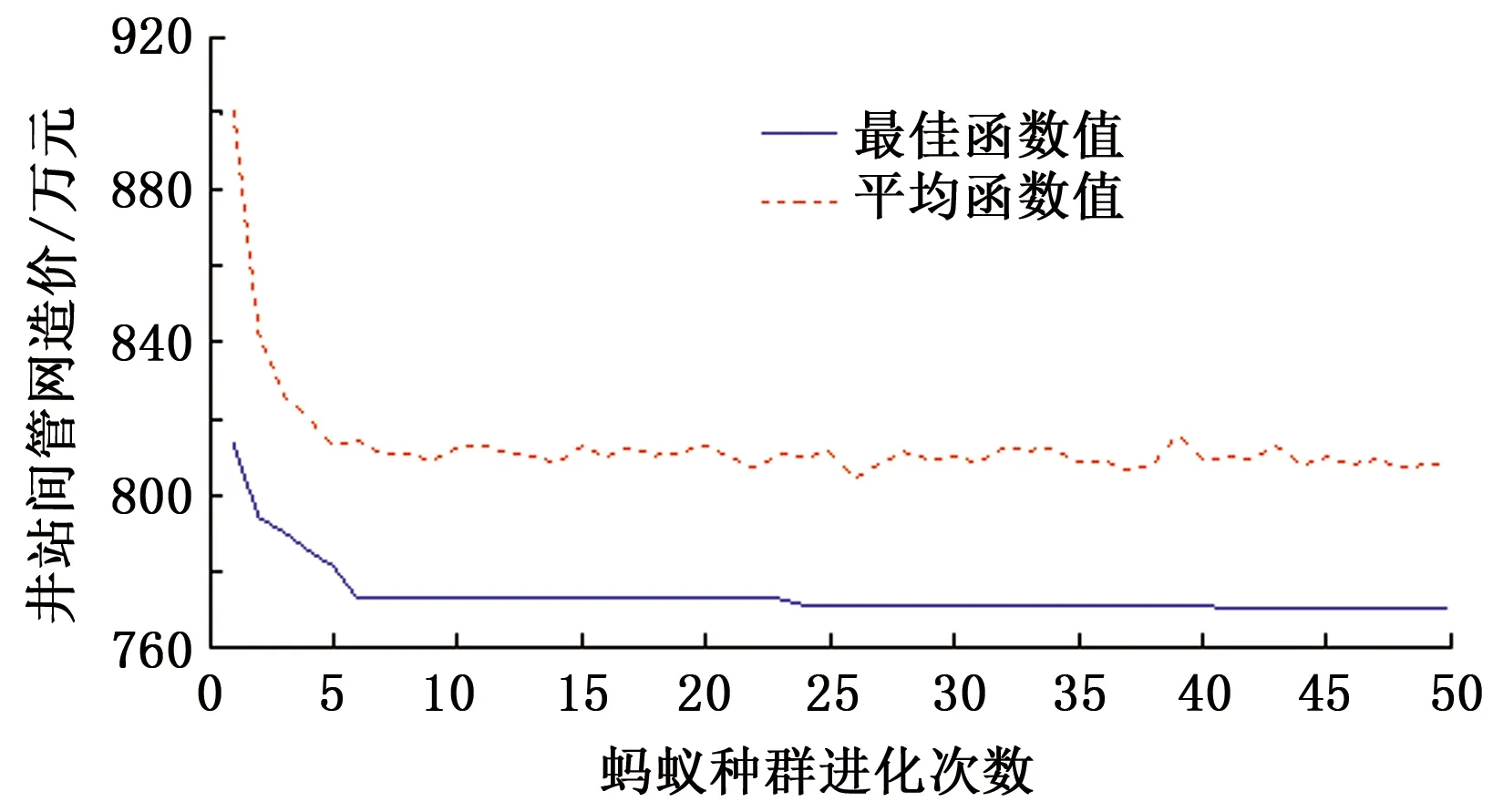
图4 蚁群算法优化过程函数值变化趋势Fig.4 Trend of objective function values in ant colony algorithm

由图5可知,通过选择、交叉、变异等操作对染色体种群的进化方向进行控制,平均目标函数值与最佳目标函数值均有较明显的下降趋势,代表着染色体种群所包含的站址分布方案在不断向经济性较优的方向发展。重复运行程序多次,虽然每次随机给定的初始值不同,但均能得到相同的稳定值,说明所采用的整体优化求解算法鲁棒性良好,优化过程不易受计算初值的影响。

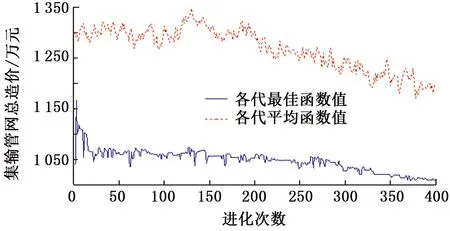
图5 遗传算法优化过程函数值变化趋势Fig.5 Trend of objective function values in genetic algorithm

5 结 论

(1)建立的以建设成本最低为目标函数的星状集输管网拓扑结构优化模型充分利用星状集输管网中同级别管段参数互不影响的特点,在井口回压、管长等约束条件下计算管线成本,从而使优化模型体现管网建设经济性。

(2)用蚁群算法与遗传算法相结合的嵌套算法实现连接关系、站点位置和管线参数的同步优化。其中,将井组划分转化为路径选择问题后用蚁群算法求解,通过提取优质解和建立窗口数组克服其易陷入局部最优、优化速度慢等不足;将站址信息以二进制编码的形式存于染色体上,变异、交叉、倒位等操作在整个布局可行域中进行,同步求得最优站址、分组方案和管线参数。

(3)整体优化算法所得布局方案的管线长度较短,管网投资较低。同时,整体优化算法寻找站址时不受初始井场分组方案的影响,将全部的布局可行域作为搜索空间,有效避免分级优化陷入局部最优的问题。

(4)算例采用的是二级布站,当集输系统中采用多级布站形式或含有多座联合时,须优化计量站或接转站的分组,该算法尚不能进行直接求解。另外,计量站等集输站点数量作为优化变量的情况也有待进一步研究。

[1] 冯叔初,郭揆常.油气集输与矿场加工[M].东营:中国石油大学出版社,2006.

[2] WANG Y, TIAN C H, YAN J, et al. A survey on oil/gas pipeline optimization: problems, methods and challenges: service operations and logistics and informatics (SOLI): IEEE International Conference on, 2012[C]. IEEE, c2012.

[3] 周军,李晓平,邓涛,等.集输系统优化设计研究的体系结构与发展方向[J].油气储运,2014,33(7):707-713.

ZHOU Jun, LI Xiaoping, DENG Tao, et al. Structure and trend of optimal design of gathering system[J]. Oil & Gas Storage and Transportation, 2014, 33(7): 707-713.

[4] 刘扬.石油工程优化设计理论及方法[M].北京:石油工业出版社,1994:114-128.

[5] 于达.原油集输规划方案的优选[J].油气田地面工程,1994,13(5):4-12.

YU Da. Planning scheme optimization of crude oil gathering and transportation[J]. Oil-Gas Field Surface Engineering, 1994,13(5):4-12.

[6] 刘扬,赵洪激,周士华.低渗透油田地面工程总体规划方案优化研究[J].石油学报,2000,21(2):88-95.

LIU Yang, ZHAO Hongji, ZHOU Shihua. A study of optimization of overall planning for surface engineering of low osmose oil field[J]. Acta, 2000,21(2):88-95.

[7] 韩建增,汪玉春.集油管网优化设计研究[J].西南石油大学学报(自然科学版),1999,21(3):52-55.

HAN Jianzeng, WANG Yuchun. A study of optimal design of oil gathering pipeline network[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 1999,21(3):52-55.

[8] 罗叶新,张宗杰,王喜,等.油田地面集输系统布局优化模型[J].油气储运,2014,33(9):1004-1009.

LUO Yexing, ZHANG Zongjie, WANG Xi, et al. Layout optimization model of surface gathering system in oilfield[J]. Oil & Gas Storage and Transportation, 2014,33(9):1004-1009.

[9] ONWUNALU J E, DURLOFSKY L J. A new well-pattern-optimization procedure for large-scale field development[J]. SPE Journal, 2011,16(3):594-607.

[10] 刘扬,魏立新,李长林,等.油气集输系统拓扑布局优化的混合遗传算法[J].油气储运,2003,22(6):33-36.

LIU Yang, WEI Lixin, LI Changlin, et al. Topological optimization of oil-gas gathering and transforming system with hybrid algorithm[J]. Oil & Gas Storage and Transportation, 2003,22(6):33-36.

[11] 杨建军,战红,刘扬,等.星状原油集输管网拓扑优化的混合遗传算法[J].西南石油大学学报(自然科学版),2008,30(4):166-169.

YANG Jianjun, ZHAN Hong, LIU Yang, et al. Hybrid genetic algorithm for topology optimization of stellated oil gathering and transportation pipeline network[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2008,30(4):166-169.

[12] 李自力,孙云峰,张子波,等.基于遗传算法的气田集输管网整体优化方法[J].天然气工业,2011,31(8):86-89,137.

LI Zili, SUN Yunfeng, ZHANG Zibo, et al. A global optimization method based on genetic algorithms for gas gathering pipeline network in a gas field[J]. Natural Gas Industry, 2011,31(8):86-89,137.

[13] 黎彬,张烈辉,唐海燕,等.基于微粒群算法的井组划分方法[J].油气田地面工程,2008,27(2):36-37.

LI Bin, ZHANG Liehui, TANG Haiyan, et al. A method for well group division based on particle swarm algorithm[J]. Oil-Gas Field Surface Engineering, 2008,27(2):36-37.

[14] 冷建成,刘扬.基于神经网络方法的油气集输管网拓扑优化设计[J].石油规划设计,2001,12(6):7-9.

LENG Jiancheng, LIU Yang. The topology optimization of oil-gas gathering and transportation[J]. Petroleum Planning & Engineering, 2001,12(6):7-9.

[15] 王洪元,卜莹,潘操.基于遗传蚁群算法的气田集输管网优化方法[J].计算机与应用化学,2012,29(12):1495-1498.

WANG Hongyuan, BU Ying, PAN Cao. An optimization method based on GA-ACA for gas gathering pipeline network in a gas field[J]. Computers and Applied Chemistry, 2012,29(12):1495-1498.

[16] 梁潇.基于遗传算法的油气管道线路优化研究[D].成都:西南石油大学,2015.

LIANG Xiao. Optimization research of oil and gas pipeline route based on genetic algorithm[D]. Chengdu: Southwest Petroleum University, 2015.

[17] 李自力,孙云峰,张子波,等.普光高含硫气田集输管网优化[J].石油学报,2011,32(5):872-876.

LI Zili, SUN Yunfeng, ZHANG Zibo, et al. Optimization design of a gathering pipe network of natural gas with high H2S from the Puguang gas field[J]. Acta, 2011,32(5): 872-876.

[18] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 1996,26(1):29-41.

[19] ZECCHIN A C, MAIER H R, SIMPSON A R, et al. Ant colony optimization applied to water distribution system design: comparative study of five algorithms[J]. Journal of Water Resources Planning and Management, 2007,133(1):87-92.

[20] OSTFELD A, TUBALTZEV A. Ant colony optimization for least-cost design and operation of pumping water distribution systems[J]. Journal of Water Resources Planning and Management, 2008,134(2):107-118.

[21] GURPREET S, NEERAJ K, ANIL K V. Ant colony algorithms in MANETs: a review[J]. Journal of Network and Computer Applications, 2012,35:1964-1972.

[22] CHEBOUBA A, YALAOUI F, AMODEO L, et al. New method to minimize fuel consumption of gas pipeline using ant colony optimization algorithms: service systems and service management: International Conference on, 2006[C]. IEEE, c2006.

[23] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005:119-125.

[24] 李炳宇,萧蕴诗.基于模式求解旅行商问题的蚁群算法[J].同济大学学报(自然科学版),2004,31(11):1348-1352.

LI Bingyu, XIAO Yunshi. Ant colony algorithm based on model algorithm for traveling salesman problem[J]. Journal of Tongji University (Science & Technology Edition), 2004,31(11):1348-1352.

[25] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies:proceedings of the First European Conference on Artificial Life [C]. Paris, 1991.

[26] 魏立新,刘扬.油气集输系统障碍拓扑布局优化设计方法[J].石油学报,2006,27(6):120-124.

WEI Lixin, LIU Yang. Obstacle topological layout optimization design of oil-gas gathering and transferring system[J], Acta, 2006,27(6):120-124.

[27] 马孝义,范兴业,赵文举,等.基于整数编码遗传算法的树状灌溉管网优化设计方法[J].水利学报,2008,39(3):373-379.

MA Xiaoyi, FAN Xingye, ZHAO Wenju, et al. Tree-type pipe network optimization design method based on integer coding genetic algorithm[J]. Journal of Hydraulic Engineering, 2008,39(3):373-379.

(编辑 沈玉英)

Global optimization of topological structure for radial pattern gathering pipe network

LIU Gang1, XU Jikai2, GUO Zhigang3, CHEN Lei1, LU Xingguo1, TENG Houxing1, XU Ruiyu1

(1.CollegeofPipelineandCivilEngineeringinChinaUniversityofPetroleum,Qingdao266580,China; 2.ShandongProvinceGasPipelineCompanyLimited,Jinan250101,China; 3.OilGasGatheringandTransportationGeneralFactoryofShengliOilfieldBranch,SINOPEC,Dongying257000,China)

The topological structure optimization model of radial patter oil and gas gathering pipe network was built according to its structural characteristics, with the total construction cost of the pipe network as the objective function, and the connection relation of nodes, pipeline parameters and location of stations as the optimization variables. To avoid the deficiency of multilevel optimization, ant colony algorithm and genetic algorithm were combined to solve the optimization model globally. In ant colony algorithm, the determination of connection relation was converted to the routing problem, heuristic factor was expressed as the function of pipe construction cost, and the total construction cost of pipe network corresponding to the routing scheme was used to calculate the pheromone accumulation. In genetic algorithm, the information of station location was stored in chromosomes using gray code, and the well-group scheme and pipe diameters were obtained by ant colony algorithm and were used to calculate the fitness of each chromosome. Meanwhile, the optimal station location, optimal well-group and pipeline parameters were also obtained. The above algorithm was applied to the optimum calculation of the specific gathering pipeline networks in some oil fields. The results show that the global optimization algorithm has better optimum quality and stronger robustness than multilevel optimization, and the optimum results are not affected by initial value.

gathering pipe network;topological structure;multilevel optimization;global optimization;ant colony algorithm;genetic algorithm

2015-12-26

刘刚(1975-),男,教授,博士,博士生导师，研究方向为油气储运工程。E-mail: liugang@upc.edu.cn。

1673-5005(2016)04-0133-08

10.3969/j.issn.1673-5005.2016.04.018

TE 863

A

刘刚,许继凯,国志刚,等.星状集输管网拓扑结构的整体优化[J]. 中国石油大学学报(自然科学版),2016,40(4):133-140.

LIU Gang, XU Jikai, GUO Zhigang, et al. Global optimization of topological structure for radial pattern gathering pipe network[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(4):133-140.