基于固态切换开关的感应电机类负荷电源快速切换新策略及参数计算

崔学深 张自力 王泽忠 李和明 杨娅萍



基于固态切换开关的感应电机类负荷电源快速切换新策略及参数计算

崔学深1张自力2王泽忠1李和明1杨娅萍3

（1. 华北电力大学电气与电子工程学院 北京 102206 2. 国网邯郸供电公司 邯郸 056002 3. 国网河北成安县供电公司 成安 056700）

舰船、电厂和钢铁等生产中的重要负荷感应电机失电后要求快速地切换至备用电源，但这类动态负荷在不利条件下所带来的瞬态冲击会产生严重的后果。为解决这一问题，提出一种基于固态切换开关（SSTS）的感应电机类负荷电源快速切换控制新策略，其在各种备用电源与主电源间相位差下，既能够快速将关键负荷从主电源切换至备用电源上，又能够有效抑制电源切换中的瞬态冲击；然后，深入分析了备用电源投入控制过程中感应电机的复杂瞬态，重点讨论了影响瞬态冲击抑制的主要因素；此外，还研究计算了已知备用电源与主电源间具有相位差时控制参数与电流峰值之间的关系，并根据电流抑制需求确定控制参数；最后，通过定子电流计算结果和实测波形，验证了所提电源快速切换控制策略及参数计算的正确性和有效性。

电源快速切换新策略 固态切换开关 控制参数 限流 感应电机

0 引言

大型工矿企业的重要负荷对供电可靠性的要求越来越高，如舰船、电厂、钢厂、化工及其他制造业生产中的某些关键感应电机类负荷，常同时配置两路以上的独立电源，以保证重要拖动系统的连续稳定运行[1-4]。在正常情况下，由主电源向感应电机供电，当主电源出现故障或者例行检修等问题时，需立即切换到备用电源上，实现高可靠不停电操作，且不允许有长时间掉电、转速大幅度下降等情况发生。此外，在主电源恢复正常后，需要再次进行电源切换，将电机恢复为主电源供电。然而，当备用电源与主电源间相位差较大时，感应电机电源切换中会出现较严重的瞬态冲击问题[5-7]，对其所在的供电系统和电机设备都会造成损害，轻者影响生产，重者造成重大经济损失甚至危及人身安全。

目前，主要使用自动转换开关（Automatic Transfer Switch, ATS）来实现感应电机的电源切 换[8]，并采用快速切换、同期捕捉切换和残压切换这三种常见电源切换方式来抑制瞬态冲击[9-15]。但是由于ATS多为机械转换开关，其固有特性使得切换时间过长、可控性差，且存在触头松动、起弧等现象[16]，这些缺点及三种常见切换方式适用条件限制了其应用。为克服这些问题，以固态切换开关（Solid State Transfer Switch, SSTS）代替ATS这种机械开关，再利用SSTS的可控性，从而可以根据实际需求设计灵活多变的控制方法。对此，文献[17-19]初步进行了这一系列的研究。其中，文献[17]针对感应电机转速近似同步速时的重合闸问题，基于SSTS设计了一种电源快速软投入方法，能够快速实现重合闸，并抑制其中的瞬态冲击，但其控制策略和参数较为复杂，控制过程也相对较长。文献[18,19]在文献[17]的基础上，进一步简化、改进SSTS控制策略，针对感应电机重合闸和电源切换提出了一种较为简单的分相快速投入控制方法，尤其适合于重合闸或者备用电源与主电源相位差不大的情况，但对于两电源相位差较大时，其控制冲击效果并不好。

基于以上研究结果，本文提出一种基于SSTS的感应电机电源快速切换控制新策略，它可以在各种备用电源与主电源相位差下，尤其是相位差较大时，快速实现感应电机类负荷无冲击地进行电源快速切换。相对文献[17]中的电源快速软投入，该方法控制参数较少、控制策略简单易行。相对文献[18, 19]中的分相快速投入，其抑制瞬态冲击的效果更好，且控制过程持续时间位于两者之间。此外，本文还深入分析备用电源投入控制过程中感应电机的复杂交替瞬态过程，重点讨论控制参数对各阶段定子瞬态电流峰值的影响。然后，在已知相位差下研究计算控制参数与电流峰值之间的关系，并基于限流思想确定控制参数。最后通过实验结果验证所提出的电源快速切换控制新策略及参数计算是正确可行的。

1 感应电机电源快速切换控制新策略

基于SSTS的感应电机电源快速切换系统主接线如图1所示，图1中KM1和KM2为断路器，SCRs1和SCRs2为三相反并联晶闸管组，如图1点划线框中所示，显然系统结构与SSTS相同。

以感应电机从主电源快速切换到备用电源为例，介绍所提出的感应电机类负荷电源快速切换控制新策略。开始时感应电机由主电源供电，KM1闭合、KM2断开，且两晶闸管组均不触发导通。当系统判断出需要将感应电机切换至备用电源时，首先断开KM1，同时触发导通晶闸管组SCRs1，电流转移至晶闸管，而后撤销SCRs1的触发信号。然后，通过电压互感器、CPU等判断出备用电源B相电压由正到负过零点，并以该点为备用电源投入控制的参考点。先按照初始两相触发延迟角0同时触发导通晶闸管组SCRs2中的SCRB和SCRC，再按第三相触发延迟角1触发导通SCRs2中的SCRA，之后每隔60°依次对称触发导通SCRC、SCRB和SCRA，至软切换过程结束。同时触发三相晶闸管，全投入三相晶闸管，最后再将KM2闭合，停止旁路晶闸管组SCRs2的触发脉冲。这样就完成了感应电机从主电源快速切换到备用电源的过程，并抑制了其瞬态冲击电流。在这种控制策略实施下，备用电源投入中定子电流典型波形及触发脉冲如图2所示，图2中还给出了备用电源B相电压波形（实际值的1/30）和晶闸管触发序列，该图形象展示了两个控制参数0和1的定义以及晶闸管触发序列。

图2 备用电源投入中定子电流典型波形及触发脉冲

感应电机这种电源快速切换控制策略，是通过控制备用电源投入过程中晶闸管的导通，并利用晶闸管自然过零关断的特性，使得感应电机定子绕组与备用电源相接通的相数在两相、三相之间交替变化，即感应电机运行状态在两相不对称瞬态和三相对称瞬态交替变化，使磁通（或者磁链）接近平滑地按照开螺旋的轨迹过渡到稳态，从而实现一种快速调压的效果，最终消除瞬态冲击，因此，也将该快速切换称为“快速软切换”。

2 影响备用电源投入控制的因素分析

由感应电机电源快速切换控制策略及图2所示的典型受控定子电流波形可知，备用电源投入控制中感应电机运行状态呈现复杂交替变化特点，具体如图3所示。备用电源投入感应电机之前，先将电流从KM1转移至SCRs1，然后撤销SCRs1的触发脉冲，从而切除主电源，这时感应电机首先进入转子自由运动过程。当系统按照初始触发延迟角0控制SCRs2中的SCRB和SCRC同时导通后，备用电源投入控制开始，这时感应电机进入“初始B、C两相不对称瞬态”；当系统以第三相触发延迟角1控制SCRs2中的SCRA导通时，感应电机进入“初始三相对称瞬态”。此后，感应电机交替出现两相不对称瞬态和三相对称瞬态，其中，感应电机两相不对称瞬态是某相定子绕组电流过零导致对应相中的晶闸管组自然关断的结果，而三相对称瞬态则是按对称触发策略控制已关断晶闸管组再次导通的结果。结合图2和图3可以发现，控制参数0决定“初始B、C两相不对称瞬态”中的电流波形及电流峰值，而1则决定“初始三相对称瞬态”及紧随其后的A、B两相不对称瞬态中的电流波形及电流峰值。

图3 备用电源投入控制中感应电机运行状态变化

除控制参数0和1以外，还存在影响感应电机电源快速切换控制的客观因素，主要有电机转速、备用电源投入时的转子电流以及备用电源与定子残压间的相位差。然而，由于所提电源快速切换中感应电机断电过程较为短暂，大约1～2个周波，故一般可近似认为转子转速不变。在一定转速下，感应电机断电过程中的转子电流与定子残压一一对应，但由于断电时间短暂，可认为定子残压几乎不衰减，近似等于主电源电压。转子电流大小和相位均取决于断电瞬间的主电源电压幅值和相位，因此，在以备用电源电压为参考时，转子电流对感应电机电源快速软切换瞬态过程的影响最终取决于备用电源与主电源的相位差。

综上分析可得，为了在不同客观因素下均能有效抑制电源切换中的瞬态冲击，需在已知备用电源与主电源相位差下研究计算控制参数0和1，其中相位差是通过互感器测量得到的，不是本文重点，不再细述。

3 控制参数的计算方法

3.1 初始两相触发延迟角a0的计算

本节使用感应电机两相不对称瞬态空间矢量数学模型，先求解出定子电流表达式，然后研究计算初始两相不对称瞬态中电流峰值与初始触发延迟角0之间的关系，再根据电源快速软切换的限流要求，求出对应的0。

通过分析可知，当系统以初始两相触发延迟角0来控制晶闸管SCRB和SCRC导通时，电机过渡到B、C两相不对称瞬态阶段，该阶段的“初值”为转子自由运动阶段的“终值”，由第2节分析可知，近似认为初始两相不对称瞬态的初值等于电机断电瞬间的转子电流值。由文献[20]可知，恒速下感应电机定子B、C两相绕组接通电源时的两相不对称瞬态空间矢量数学模型为

式中，BC为备用电源施加于电机定子绕组B、C两相间的线电压；为定子电流空间矢量；、分别为归算到定子侧的转子电流空间矢量及其共轭分量；s、s分别为定子每相绕组的电阻和总电感；r、r分别为归算到定子侧的转子每相绕组的电阻和总电感；m为电机互感参数；r为转子电角速度；为微分算子，=dd。

其中

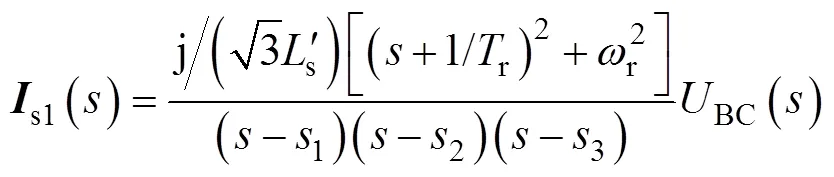
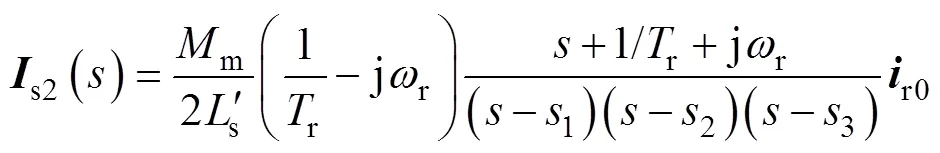
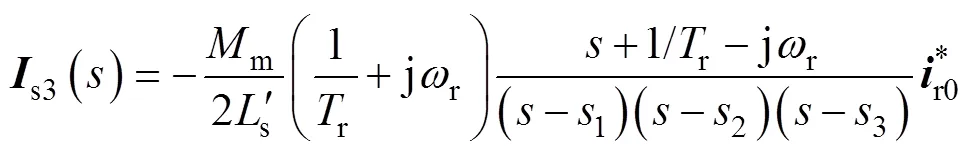
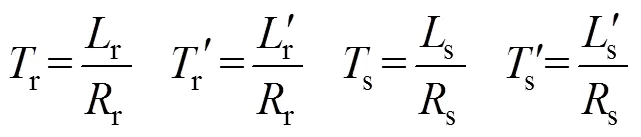
1、2和3是一元三次方程

的特征根，可利用卡丹公式[21,22]、牛顿切线法[23]等求得。对实验电机而言，该方程有一个实数根和两个共轭复根，分别记为

则备用电源B、C两相间线电压为

对式（2）进行拉普拉斯反变换，可求得定子电流空间矢量的时域表达式为

其中

式中，系数s1k（=1, 2, 3, 4, 5）是由备用电源电压BC决定的，它们是初始两相触发延迟角0和相位差的函数；而余下系数则是由该阶段转子电流初值决定，即近似由感应电机从主电源断开瞬间的转子电流值决定，于是，在感应电机断电位置确定不变时，这些系数为常数。

考虑到初始B、C两相不对称瞬态阶段中定子A相电流恒为零，即，则，再根据空间矢量和三相变量之间的关系[24,25]，并结合式（6），可求得电源快速软切换中感应电机初始B、C两相不对称瞬态中定子电流的表达式为

由上文分析知，式（8）中的系数s1k（=1, 2, 3, 4, 5）受0和的影响，其余系数近似常数不变，因此该阶段中电流波形及其峰值m1由0和决定。当相位差确定不变时，通过式（8）可以计算得到m1与0间的关系曲线，其结果如图4所示。图4中给出了分别为120°、180°和-120°时m1和0之间的关系。若要求该阶段电流峰值m1不超过某个限流值，则可通过图4所示关系曲线确定对应的触发延迟角0。例如，限流值为6.5A时，三种相位差下的初始触发延迟角应该分别取60°、92°和113° 左右。

图4 im1与a0间的关系曲线

3.2 定子第三相初始触发延迟角a1的计算

由第2节分析结果可知，在根据首半波限流值确定0后，第三相触发延迟角1决定“初始三相对称瞬态”及紧随其后的A、B两相不对称瞬态中的电流波形及电流峰值。其中A、B两相不对称瞬态是由于“初始三相对称瞬态”中定子C相绕组电流过零导致晶闸管组SCRC自然关断的结果。该过程持续到SCRC再次触发导通瞬间，由第1节易知，感应电机这两个阶段持续时间之和为1p/3。本节采用与2.1节类似的办法，使用感应电机对称、不对称空间矢量数学模型，研究计算这两个阶段中的电流峰值与1的关系，再根据限流值确定对应的1。

由文献[20,24,25]知，描述感应电机“初始三相对称瞬态”及紧随其后的A、B两相不对称瞬态的空间矢量数学模型分别为

再根据后一阶段的“初值”等于前一阶段的“终值”这一原则来确定这两个阶段的定、转子电流初值，就可使用与2.1节类似的办法求解出定子电流空间矢量时域表达式，具体过程略，定子三相电流计算如下[24,25]。

在初始触发延迟角0确定后，可根据这两个阶段中所推导的定子电流表达式，计算得到不同相位差下的电流峰值m2与第三相触发延迟角1间的关系曲线，其结果如图5所示，图5给出的分别是= 120°、0=60°，=180°、0=92°及=-120°、0= 113°这三种情况下的结果，由该关系曲线，可以根据该阶段限流值确定第三相触发延迟角1。一般地，要求电源快速软切换中后续各阶段电流峰值不超过上一阶段电流峰值，如该阶段电流限流值取6A时，三种情况下的第三相触发延迟角1应该分别取为 132°、162°和185°左右。

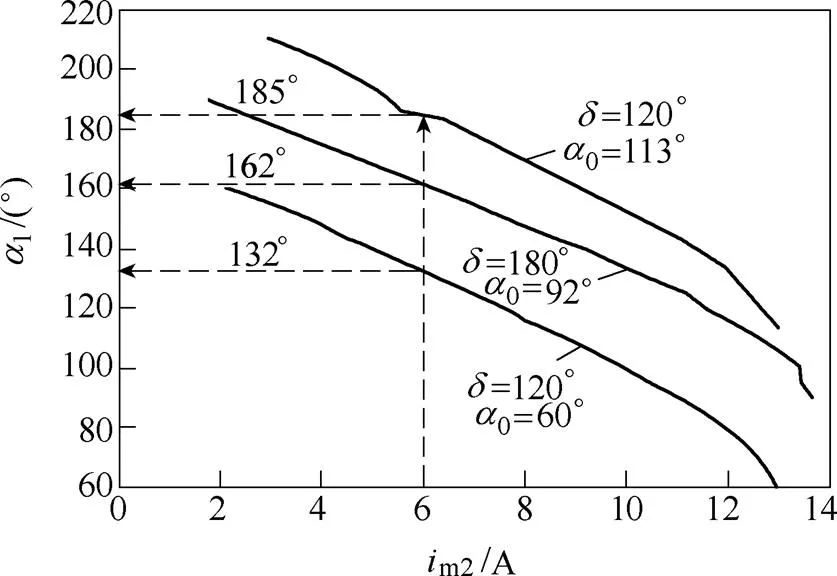
图5 im2与a1间的关系曲线

需要说明的是，在根据电流峰值确定控制参数0和1时，限流值既不能选得太大，也不能太小，因为太大起不到限流作用，太小会导致后续各阶段中电流峰值很大，并超过这两个初始阶段的电流峰值。研究发现，初始两阶段的限流值一般取为额定电流的1.5倍左右比较合适。

4 感应电机电源快速切换实验

上文中所给波形都是基于实验电机而言的，其为一台2.2kW的笼型感应电机，在分析过程中将笼型转子等效为绕线式转子，额定电压为380V，额定电流为4.8A，定、转子每相绕组电阻分别为6.92W、7.36W（折合到定子侧的值），定、转子每相绕组漏电抗均为14.1W，励磁电阻为36.3W，励磁电抗为486.7W，频率为50Hz，极对数为2，转动惯量为0.005kg·m2。

（a）A相电流

（b）B相电流

（c）C相电流

图6=120°时备用电源投入中定子电流计算和实测结果

Fig.6 Calculation and test results of the stator currents during the switching of alternate source with=120°

由图6可见，快速软切换中定子电流明显小于直接切换中的电流，说明了所提电源快速软切换方法能够有效抑制冲击电流。感应电机快速软切换中定子电流计算结果与实测波形基本一致，验证了所提电源软切换方法是正确可行的，也说明了控制参数的计算是正确的。此外还能够看出，感应电机电源软切换能够在2～3个周波内实现，说明了所提出的电源软切换方法是非常快速的。

（a）=180°

（b）=-120°

图7=180°和-120°时备用电源投入中定子电流实测结果

Fig.7 Test results of the stator currents during the switching of alternate source with=180°and=-120°

5 结论

通过实验室小功率感应电机的实验结果，验证了本文所提感应电机电源快速切换控制新策略的正确性和可行性，其既能在2～3个周波内快速实现感应电机的电源切换，又能有效地将瞬态冲击电流控制在1.5倍额定值以内，该方法尤其能够实现备用电源与主电源间相位差较大时的电源快速软切换，至于大功率电机的应用效果还需进一步研究分析。此外，还在已知备用电源与主电源相位差下，计算研究了备用电源投入控制过程中参数与电流峰值之间的关系，并根据限流值来确定控制参数。

所提出的基于SSTS的感应电机电源快速切换控制新策略，不仅赋予了SSTS新的意义，而且丰富了电源软切换方法体系，能够与快速切换、同期切换和残压切换这三种常见电源切换方式配合使用，更完善地解决了感应电机电源切换中的瞬态冲击问题，为实际生产提供理论参考和指导，具有工程应用价值。

参考文献

[1] Goswami A K, Gupta C P, Singh G K. Voltage sag assessment in a large chemical industry[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1739-1746.

[2] 王焕文. 舰船电力系统及自动装置[M]. 北京: 科学出版社, 2004.

[3] Hornak D L, Zipse D W. Automated bus transfer control for critical industrial processes[J]. IEEE Transactions on Industry Applications, 1991, 27(5): 862-871.

[4] 王璐, 周海潇, 罗建, 等. 感应电动机电源切换的UPS逆变器控制策略[J]. 电力系统保护与控制, 2014, 42(24): 49-55.

Wang Lu, Zhou Haixiao, Luo Jian, et al. Control strategy of UPS for the induction motor[J]. Power System Protection and Control, 2014, 42(24): 49-55.

[5] Balamourougan V, Sidhu T S, Kasztenny B, et al. Robust technique for fast and safe transfer of power plant auxiliaries[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 541-551.

[6] Pettigrew R D, Powell P, Burnworth J, et al. Motor bus transfer[J]. IEEE Transactions on Power Delivery, 1993, 8(4): 1747-1758.

[7] 崔学深, 张自力, 李和明, 等. 感应电机电源切换中残压和电压差的研究及最优切换策略[J]. 电工技术学报, 2015, 30(2): 162-171.

Cui Xueshen, Zhang Zili, Li Heming, et al. Residual voltage, voltage difference and optimal switching strategy during the power switching of induction motors[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 162-171.

[8] Tian Bing, Mao Chengxiong, Lu Jiming, et al. 400V/ 1000kV·A hybrid automatic transfer switch[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5422-5435.

[9] Beckwith T R, Hartmann W G. Motor bus transfer: considerations and methods[J]. IEEE Transactions on Industry Applications, 2006, 42(2): 602-611.

[10] Higgins T A, Snider W L, Young P L, et al. Report on bus transfer I assessment and application[J]. IEEE Transactions on Energy Conversion, 1990, 5(3): 462- 469.

[11] Higgins T A, Young P L, Snider W L, et al. Report on bus transfer II computer modeling for bus transfer studies[J]. IEEE Transactions on Energy Conversion, 1990, 5(3): 470-476.

[12] Young P L, Snider W L, Higgins T A, et al. Report on bus transfer III full scale testing and evaluation[J]. IEEE Transactions on Energy Conversion, 1990, 5(3): 477-484.

[13] 高雅, 刘卫国, 骆光照. 大惯量负载永磁同步电机断电-寻优重投控制系统[J]. 电工技术学报, 2014, 29(5): 62-69.

Gao Ya, Liu Weiguo, Luo Guangzhao. A large inertia load PMSM power down-rejoining on optimizing control system[J]. Transactions of China Electro- technical Society, 2014, 29(5): 62-69.

[14] Young C C, Dunki-Jacobs J. The concept of in-phase transfer applied to industrial systems serving essential service motors[J]. American Institute of Electrical Engineers, Part II: Transactions of the Applications and Industry, 1961, 79(6): 508-518.

[15] Kelly A R. Relay response to motor residual voltage during automatic transfers[J]. American Institute of Electrical Engineers, Part II: Transactions of the Applications and Industry, 1955, 74(4): 245-252.

[16] 王松岑, 汤广福, 于坤山, 等. 新型中压固态切换开关的研究[J]. 电网技术, 2006, 30(增): 311-315.

Wang Songcen, Tang Guangfu, Yu Kunshan, et al. Development of a novel medium voltage solid state transfer switch[J]. Power System Technology, 2006, 30(S): 311-315.

[17] 崔学深, 罗应立, 周振华, 等. 感应电动机的电源快速软投入技术及其初始瞬态解析[J]. 中国电机工程学报, 2009, 29(6): 93-99.

Cui Xueshen, Luo Yingli, Zhou Zhenhua, et al. Rapid soft re-switching technique of three-phase induction motors and its initial transient analytical method[J]. Proceedings of the CSEE, 2009, 29(6): 93-99.

[18] 吴玲. 感应电机在电源切换时分相投入控制的理论研究[D]. 北京: 华北电力大学, 2009.

[19] 李卫国, 崔学深, 罗应立, 等. 感应电机快速投入控制参数的解析[J]. 电工技术学报, 2013, 28(3): 154-160.

Li Weiguo, Cui Xueshen, Luo Yingli, et al. Analytical method on control parameter of quick switching on induction motor load[J]. Transactions on China Electrotechnical Society, 2013, 28(3): 154-160.

[20] 李和明, 张自力, 崔学深, 等. 晶闸管-电动机系统不对称瞬态建模及解析[J]. 电工技术学报, 2013, 28(8): 241-249.

Li Heming, Zhang Zili, Cui Xueshen, et al. Asymmetrical transient modeling and analytical research of SCR-motor systems[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 241- 249.

[21] 崔学深. 感应电机电源软投入相关理论及节能控制新技术的研究[D]. 北京: 华北电力大学, 2009.

[22] 马明. 塔塔利亚与三次方程的故事[J]. 数学史话, 2001 (27): 14-16.

Ma Ming. The story of Tatalia and the cubic equation[J]. Myth of Mathematics, 2001(27): 14-16.

[23] 罗炜, 崔学深, 罗应立. 感应电机不对称暂态分析中一类一元三次特征方程及其近似求解[J]. 中国电机工程学报, 2008, 28(27): 126-130.

Luo Wei, Cui Xueshen, Luo Yingli. Approximate solutions of a class of cubic characteristic equations in asymmetric transient analysis of induction machines[J]. Proceedings of the CSEE, 2008, 28(27): 126-130.

[24] Novotny D W, Lipo T A. Vector control and dyna- mics of AC drives[M]. New York: Clarendon Press Oxfard, 1996.

[25] Krause P C, Wasynczuk O, Sudhoff S D. Analysis of electric machinery and drive systems[M]. New York: Wiley-IEEE Press, 2002.

Novel Rapid Power Switching Strategy and Its Parameter Calculation of Induction Motor-Load Based on Solid State Transfer Switch

12113

（1. School of Electrical and Electronic Engineering North China Electric Power University Beijing 102206 China 3. State Grid Handan electric Power Supply Company Handan 056002 China 2. State Grid Heibei Cheng’an Electric Power Company Cheng’an 056700 China）

As an important load of naval vessels, electric plants and steel plants, induction motor should be switched rapidly from main source to alternative source after its power outages. However, the transient inrush produced by such dynamic load under the adverse conditions would have serious consequences. Accordingly, a novel rapid power switching control strategy of induction motor load was proposed based on solid state transfer switch (SSTS) in this paper. The proposed strategy could not only rapidly transfer the critical load from main source to alternative source, but also effectively suppress the transient inrush under the condition of the various phase-angle differences between the two sources. Then, the complex transient of induction motor during the switching control process of the alternative source was analyzed. And the main factors affecting the suppression of the transient inrush were discussed. Besides, the relationship between control parameters and current peak values was explained when the phase-angle difference between the two sources was known. The control parameters could be obtained by the requirement of the current-limit suppression. Finally, the calculation and test results of the stator currents verified that the proposed rapid power switching strategy and the parameters calculation were correct and effective.

Novel rapid power switching strategy, solid state transfer switch, control parameters, current limit, induction motor

TM32；TM346

崔学深 男，1973年生，副教授，主要研究方向为交流电机过渡过程分析与控制。

E-mail: cxs@ncepu.edu.cn

张自力 男，1985年生，博士研究生，主要研究方向为电源快速软投入、软切换和交流电机过渡过程分析与控制等。

E-mail: zhangzili@ncepu.edu.cn（通信作者）

2015-08-12 改稿日期 2016-01-02

中央高校基本科研业务费专项资金（13XS06）和国家自然科学基金（51077048）资助项目。