基于三维空间域的宏小区移动通信正向链路信道参数估计*
周杰 姚颖莉 罗宏 朱伟娜 菊池久和
(1.南京信息工程大学 江苏省气象探测与信息处理重点实验室, 江苏 南京210044;2.日本国立新泻大学 工学部电气电子工学科, 日本 新泻950-2181)
基于三维空间域的宏小区移动通信正向链路信道参数估计*
周杰1,2姚颖莉1罗宏1朱伟娜1菊池久和2
(1.南京信息工程大学 江苏省气象探测与信息处理重点实验室, 江苏 南京210044;2.日本国立新泻大学 工学部电气电子工学科, 日本 新泻950-2181)
针对均匀分布的三维(3D)散射簇移动通信环境,提出了3D空间域的统计信道模型;在指向性天线覆盖下的宏小区通信环境中,用该模型来估计多径衰落信道的重要空时信道参数,推导了多径衰落信道正向信道链路的到达角与到达时延的概率密度函数、由移动台(MS)移动产生的多普勒频移(DS),分析了空间信道参数及其定向天线主瓣宽度对信道模型的影响.假设MS端散射体分布为高斯分布和指数分布时,该模型更适于描述特殊的移动通信环境.数值仿真结果表明,该模型的信道参数估计符合理论及实际的通信环境,弥补了现有三维散射簇统计信道模型的局限性.
统计信道模型;到达角;到达时延;多普勒频移;多径衰落
移动通信的本质是利用无线通信进行信息的有效传输,其系统性能主要受无线信道特性的制约.因此,构建能够准确而有效描述无线传输系统中多径效应的信道模型,对移动通信系统而言至关重要[1-2],同时也是分析信道空时特性的前提条件.由于信道的复杂性和时变性,建立准确的确定性信道模型较为困难,因此一般采用统计模型.人们相继提出了不同的统计信道模型,并假设不同的散射体分布或空间几何分布,用于对室内、外环境中的信道多径效应进行仿真分析.其中只经历一次反射的散射模型应用最为广泛[3-11].文献[3-4]分别提出了通用的空间分布圆模型和椭圆模型.文献[5-6]提出了一个散射体中心在移动台(MS)处,基站(BS)与MS均置于圆内的圆模型来仿真室内通信环境.文献[7]基于散射体均匀分布的假设提出了空心圆环模型.但以上模型的研究与分析都只停留在二维平面上,虽然描述简单、容易且适用于仿真特定的环境,但二维(2D)模型不能很好地描述竖直平面的波达信号变化情况,且不适合建立在移动台天线接近或低于周围建筑物的小区或城市环境中.散射波可通过从建筑物的顶部向下衍射到达街道的方式进行传输,在这种无线通信环境下,三维(3D)模型比2D模型描述得更加精确,可以将BS及MS端的波达信号细化为水平面以及垂直面的空间角域.因此,文献[8]提出了一种基站处设置指向性天线且适用于宏小区的三维统计模型.文献[9]提出了一种在室内外无线环境下的三维椭球模型,但仅对水平及竖直面内的到达角(AOA)进行研究,缺乏对到达时延(TOA)及多普勒效应(DS)的研究,不能客观和详尽地描述物理信道.文献[10-11]基于传输理论的假设提出了一种新型的三维空间域模型,但该模型仅适用于室外的宏蜂窝通信环境,且在MS、BS端均只考虑全向天线阵列的影响.在文献[10-11]的基础上,文中将BS设计为指向性天线阵列,将MS附近的散射体衰减限定在二维水平面内,以使模型能更好地适应特定的宏小区城市与农村无线通信环境.
针对宏小区移动通信系统,文中提出了基于散射簇的三维统计信道模型,其MS处散射体仅分布在二维圆模型内;推导了衰落信道正向链路的概率密度分布,分析了频率变化导致的DS概率密度函数及其特征函数.
1 3D散射簇统计信道模型
文中提出的适用于宏蜂窝无线通信环境的3D散射簇统计信道模型如图1所示.其中MS与BS间的水平距离为D,MS周围的散射体均匀分布且被限制在半径为R的圆形区域(CM)内,BS处使用主瓣宽度为2α的定向天线,且与MS的水平高度差为h.图中仅标注一个散射体,但实际上可认为有许多散射体分布于CM内.指向性天线分割散射体区域,会使散射区域形成非对称的信道模型,如图2所示.

图13D散射簇统计信道模型
Fig.1Statistical channel model of 3D scattering cluster

图2信道模型的二维俯视图
Fig.22D top view of channel model
由于移动台不断微型化,对天线使用的限制也更大.在信道建模的发展过程中,已经形成了传输建模的一系列假设[12-14].这些假设适用于没有大型障碍物(如山脉、高大建筑物等)存在的宏蜂窝无线电环境中.为简化研究与分析,除了上述常规信道假设外,文中还做了如下假设:①每个散射体均为全方位反射,且独立于其他散射体,并只经历一次反射;②MS远离散射区域的边界,且忽略相邻小区的干扰;③MS和BS间的每条传输路径只与一个散射体有关.为推导MS端多普勒谱的频移特性,设定BS端使用主瓣宽度为2α的指向性天线.文中不考虑所有的天线极化的影响.
1.1正向信道链路的AOA分布函数
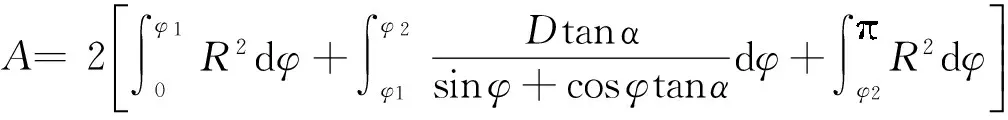
(1)
将面积分为等腰三角形和扇形两部分区域来求解,计算更为简便,式(1)可简化为
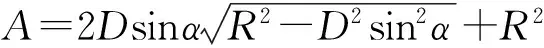
(2)
式中,φ1和φ2的角度范围如图2所示,
(3)
(4)
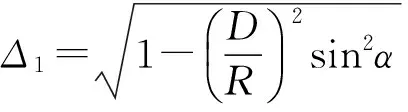

(5)
(6)
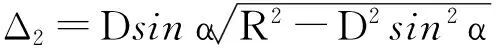
Δ4=D2tan2α(sinφ+cosφtanα)-2.
1.2正向信道链路的 TOA分布函数
如图1所示的三维散射簇模型,定义散射体点到移动台的距离为lm,到基站的距离为lb.已知散射体在三维空间信道模型内均匀分布,则散射体分布函数为
(7)
利用雅可比转换J(·)可推得p(lm,φ)的函数表达式:
(8)
对任何散射体反射的信号,从基站到移动台存在多条传播路径,其多径信号的到达时延为,
(9)
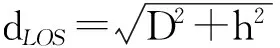
(10)
记位于散射区域最外层边界上的散射体对应的传输路径时延为lim,通过三角函数计算可以得到lb的表达式为
(11)
将式(11)代入式(9),经过计算简化可以得到在BS端仰角已知情况下lm(,φ)及lim的表达式:
lm(,
(12)
(13)
再利用雅可比转换,可以推导出MS端AOA/TOA的联合概率密度函数,即
(14)
将式(8)代入式(13),经过计算推导可得MS端方位角与到达时间的联合概率分布函数:p(,φ)=(c32-2c2
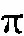
(15)
p()
(16)
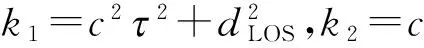
2 多普勒频移概率密度分布
在3D空间域移动通信环境中,MS的移动特性会使接收端信号产生频谱扩展,扩展程度主要是由多普勒频移特性来描述.入射信号到达角与DS之间的关系用fF来表示,即
fF=vfcsinθcos(φ-φv)/c
(17)
式中:fc为没有多普勒频移时的信号频率;v为相对移动的速度;θ和φ分别为波达信号的仰角与方位角,它们相互独立.vfc/c>0是最大多普勒频移,记为fm;在xoy水平面内,MS在距离y轴角度为φv的方向上以速度v移动.为简单起见,将多普勒频移定义为γF=fF/fm,
γF=sinθcos(φ-φv)
(18)
如上所述,文中的信道模型是由基于单反射的宏蜂窝2D统计模型扩展而来的简易3D空间域散射模型.根据以上提出的假设,所有散射体均匀分布在MS周围水平面内的一个圆模型中,因此所有到达MS端的入射信号满足:水平面内sinθ=1,竖直面内边缘概率密度函数f(βm)=0.利用随机变量变换的基本理论可容易求解正向信道链路DS分布的概率密度函数fMS(fF),即
(19)
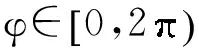
(20)
利用式(17)-(20),简单计算后可得
(21)
天线的所有波达信号都有一个相等的平均强度时,从式(21)可以得到一个相等的信号功率谱密度(PSD),此时散射信道的反向链路DS分布便可由数值计算得到.
3 数值计算结果与分析
针对文中研究的三维空间域统计信道模型,文中通过数值计算和仿真给出了指向性天线或特殊宏小区环境下到达角度空间参数等的影响情况.为不失一般性,文中定量给出该模型的D=100m,R=60m.
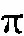
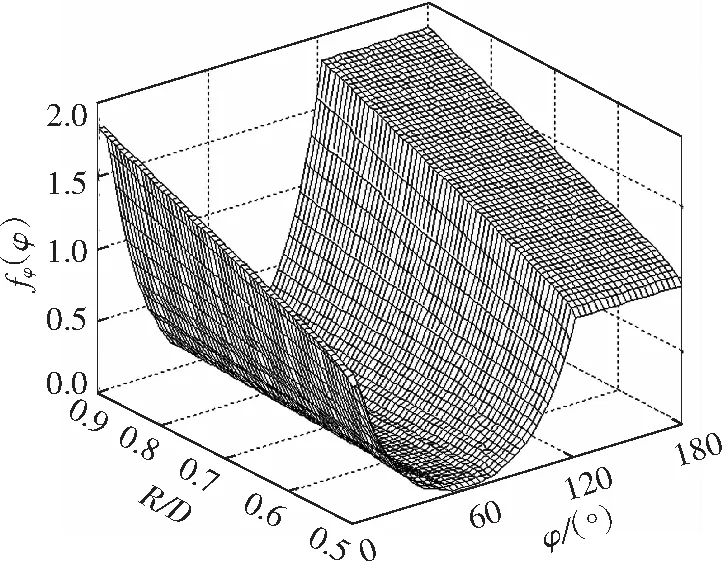
图3正向信道链路在水平面内的三维分布(D=100m)
Fig.33Ddistributionofforwardchannellinkinhorizontalplane(D=100m)
正向信道链路方位角与时延的联合概率密度分布如图4所示.从图4(a)可知,全向天线下联合概率密度的分布极大值主要集中在最小时延min和较小方位角φ的区域,在φ∈(0,)范围内,联合概率密度不断减小,且在最大角φ=处达到最小值.这是因为在φ=处,传输路径最长,传输时延较大,如图1所示.在/c)范围内不断增大时延时,xoz切平面上局部极大值对应的曲线缓慢下降并趋于极限,而同一切平面上局部极小值对应的曲线缓慢增加并趋于极限值,且局部极大值减小的速率小于极小值增加的速率.在没有定向天线的情况下,概率分布呈对称性,故在φ∈(-,0)范围内方位角的TOA概率密度分布情况与图4(a)所示的曲线对称.
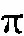
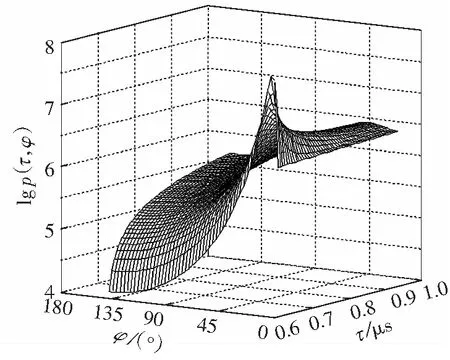
(a)α=180°

(b)α=30°
Fig.4AOA/TOAjointprobabilitydensitydistributionofforwardchannellink
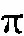

图5散射体边界的传输时延(R=60m)
Fig.5Propagationdelayofthescatteringboundary(R=60m)
上述仿真结果与Nawaz模型[15]的lim研究结果相符合,进一步验证了接收端电磁信号传输时延分布仿真结果的正确性,适用于三维无线通信环境下的时延特性理论分析.
空间参数R/D及h/D对TOA边缘概率密度分布的影响如图6所示.从图中可知:在时延从dLOS/c逐渐增大到/c的过程中,TOA分布呈递减趋势;增大MS端CM散射体分布区域的半径R,传输路径相对延长,使TOA边缘概率密度分布在时延确定的竖直线上相对增加.在h已知的情况下,TOA边缘概率密度在

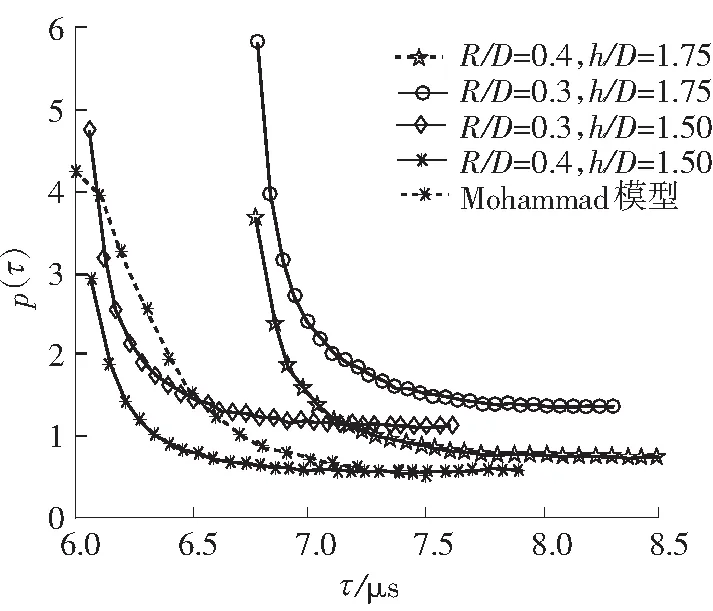
图6TOA的边缘概率密度函数分布
Fig.6Marginal probability density functiondistribution of TOA
空间参数R/D及定向天线波束宽度α对正向信道链路多普勒频移概率密度分布的影响见图7.从图中可知:当φv=90°,即MS的移动方向垂直于直达路径时,由于定向天线的波束宽度在xoz面内对称,使得MS端多普勒频移的概率密度关于频率0点左右对称分布;随着R/D的减小以及α值的增加,其概率密度分布趋于Clarke U型经典模型,且在fF=100 Hz时,MS端多普勒频移的概率密度值达到最大;伴随着信道参数R/D的增大,散射体的增多使得反射与折射概率增大,故正向链路的多普勒功率也逐渐增大,这与图3中正向链路的分析结果相符,更好地验证了本模型信道参数估计结果的合理性.
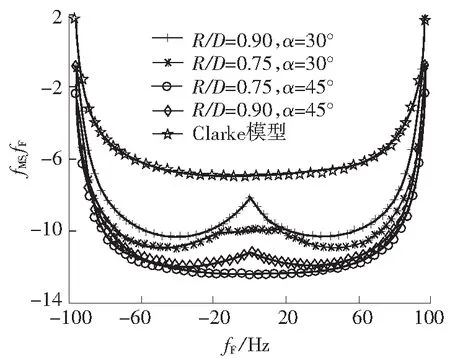
图7正向信道链路多普勒频移的概率密度分布(D=100 m,fm=100 Hz,φv=90°)
Fig.7Doppler shift probability density distribution for forward channel link(D=100 m,fm=100 Hz,φv=90°)
4 结论
针对指向性天线、宏小区通信环境造成的空间衰落信道,文中提出了一种基于散射簇的3D统计信道模型,该模型BS端的发射信号来自一个三维空间,但输入到MS端的所有信号却仅仅分布在水平面上的圆模型中,本模型弥补了设置定向天线的现有室外3D信道建模研究的不足;推导了多径衰落信道下正向信道链路的AOA/TOA概率密度函数、多普勒频移的概率密度函数,分析了空间信道参数R/D、h/D及定向天线主瓣宽度对信道模型的影响.数值仿真结果表明,该模型的信道参数估计符合理论与实际的通信环境,扩展了空间统计信道模型的研究和应用,为分析无线传输系统的空间参数及多普勒效应提供了更为灵活的模型参考.
[1]JAKES W.Microwave mobile communications [M].New York:Wiley-IEEE Press,1974.
[2]DAMNJANOVIC A,MONTOJO J,WEI Y,et al.A survey on 3GPP heterogeneous networks:wireless communications [J].IEEE Wireless Communications,2011,18(3):10-21.
[3]ERTEL R B,REED J H.Angle and time of arrival statistics for circular and elliptical scattering model [J].IEEE Journal on Selected Areas in Communications,1999,17(11):1829-1840.
[4]PETRUS P,REED J H,RAPPAPORT T S.Geometrical-based statistical macrocell channel model for mobile environment [J].IEEE Transactions on Communications,2002,50(3):495-502.
[5]JIANG L,TAN S Y.Simple geometrical-based AOA model for mobile communication systems [J].Electronics Letters,2004,40(19):1203-1205.
[6]JIANG L,TAN S Y.Geometrically based power azimuth spectrum models for mobile communication systems [J].Microwave and Optical Technology Letters,2007,49(9): 2093-2097.
[7]ZHOU J,QIU L.Analyses and comparisons of geometri-cal-based channel model arisen from scatters on a hollow-disc for outdoor and indoor wireless environments [J].IET Communications,2012,6(17):2775-2786.
[8]SYED J N,PATWARY M N.3-D Gaussian density propagation model employing a directional antenna at BS [J].IEEE Transactions on Vehicular Technology,2010,59(7):3193-3204.
[9]MOHAMMAD A,ALSEHAILI S.Generalized three dimensional geometrical scattering channel model for indoor and outdoor propagation environments [D].Winnipeg:University of Manitoba,2010.
[10]JANASWAMY R.Angle of arrival statistics for a 3D spheroid model [J].IEEE Transactions on Wireless Communications,2002,1(3):488-497.
[11]BALTZIS K B,SAHALOS J N.A simple 3D geometric channel model for macrocell mobile communication [J].Wireless Personal Communications,2009,51(2):329-347.
[12]SPENCER Q H,JEFFS B D,JENSEN M A,et al.Mode-ling the statistical time and angle of arrival characteristics of an indoor multi-path channel [J].IEEE Journal on Selected Areas in Communications,2000,18(3):347-357.
[13]QU Shouxing.An analysis of probability distribution of Doppler shift in three dimensional mobile radio environments [J].IEEE Transactions on Vehicular Technology,2009,58(4):1634-1639.
[14]KAREDAL J,ALMERS P.A MIMO channel model for wireless personal area networks [J].IEEE Transactions on Communications,2010,9(1):245-255.
[15]NAWAZ S J,QURESHI B H,KHAN N M.A generalized 3-D scattering model for a macrocell environment with a directional antenna at the BS [J].IEEE Transactions on Vehicular Technology,2010,59(7):3193-3204.
[16]BUYUKCORAK S,KURT G K.Simulation and measurement of spatial correlation in MIMO systems with ray tracing [C]∥Proceedings of the 5th International Conference on Signal Processing and Communication Systems.Gold Coast:IEEE,2011:1-5.
s: Supported by the General Program of the National Natural Science Foundation of China (61372128,61471153)
3-D Spatial Domain-Based Forward Link Channel Parameter Estimation in Macro-Cell Mobile Communication
ZHOUJie1,2YAOYing-li1LUOHong1ZHUWei-na1HISAKAUKikuchi2
(1. Jiangsu Key Laboratory of Meteorological Observation and Information Processing,Nanjing University of Information Science and Technology, Nanjing 210044, Jiangsu, China;2. Department of Electronic and Electrical Engineering, Niigata University, Niigata 950-2181, Japan)
In view of the uniform distribution of the mobile communication environment with 3D scattering clusters, a statistical channel model for 3D spatial domain is constructed in this paper. In the macro-cell communication environment covered by directional antennas, the constructed model is used to estimate the parameters of the space-time channel in the multipath fading channel, and the probability density functions (PDFs) of the angle of arrival (AOA) and the time of arrival (TOA) are derived for the forward channel link in the multipath fading channel. In addition, the Doppler shift (DS) caused by the movement of mobile stations (MSs) is also derived, and the influences of both the spatial channel parameters and the main lobe width of directional antennas on the constructed model are analyzed. When the scattering objects around MSs are assumed as the Gaussian and exponential density models, the constructed model is more suitable to describe special mobile communication environments. The numerical simulation results show that the channel parameters estimated by using the proposed model are consistent with the theoretical and actual communication environments, which makes up for the limitations of the existing statistical channel models of three-dimensional scattering clusters.
statistical channel model; angle of arrival; time of arrival; Doppler shift; multipath fading
1000-565X(2016)09-0081-06
2015-12-11
国家自然科学基金面上项目(61372128,61471153);江苏省高校自然科学研究重大项目(14KJA510001)
周杰(1964-),男,教授,博士生导师,主要从事移动通信理论、无线传感网和无线接入网研究.E-mail:zhoujie45@hotmail.com
TN 911
10.3969/j.issn.1000-565X.2016.09.012

