基于纹理与色调感知的变系数误差扩散算法*
王欣波 胡建华 王云宽 吴少泓 陆浩
(中国科学院 自动化研究所, 北京 100190)
基于纹理与色调感知的变系数误差扩散算法*
王欣波胡建华王云宽吴少泓陆浩
(中国科学院 自动化研究所, 北京 100190)
传统的误差扩散算法存在非期望的人工结构以及细节表现能力不足等缺点,为此,文中提出了一种基于纹理与色调感知的变系数误差扩散算法.首先根据图像局部视觉偏差,在图像的平坦区和纹理区分别采用噪声调制和纹理信息进行阈值修正,然后结合蓝噪声的频谱特性以及图像的空间特性,采用蚁群算法获得各灰度级下最优的误差扩散系数.实验结果表明,文中算法输出的半色调图像减少了误差扩散中存在的人工结构,保证了输出图像的纹理细节,具有较好的信噪比和结构相似度.
误差扩散;图像纹理;噪声调制;蚁群算法
近年来,随着印刷技术的发展,印刷领域发生了革命性的变化,从传统印刷走向了数字化印刷.数字半色调技术为数字印刷提供打印数据,是基于人眼的视觉特性和图像的成色特性,利用数学、计算机等工具,在二值设备或有限灰度级设备上实现图像再现的一门技术[1].目前半色调技术主要分为点处理、领域处理和迭代优化处理[2-3].其中,以误差扩散算法为代表的领域处理以其优良的半色调视觉效果和适中的运算量被认为是目前最有效的半色调技术.
自从提出了基于4系数误差滤波器的误差扩散算法[4]后,为了解决传统误差扩散算法存在的非期望的人工结构以及细节表现能力不足等缺点,众多学者对误差扩散算法的阈值模型和误差滤波器进行了改进,以提高半色调图像的输出质量.基于噪声调制的阈值模型可以在一定程度上减少“蠕虫”等人工结构的产生,但噪声的引入使得图像模糊化,细节表现能力不足.为了更好地表现纹理细节,基于图像纹理的半色调算法被相继提出,如半色调纹理优化算法[5]和基于结构感知的误差扩散算法[6],这些算法对输出图像的纹理有着较好的再现,但依然存在一定程度的人工结构.误差滤波器的优化算法可以分为自适应误差扩散算法[7-8]和基于色调的变系数误差扩散算法[9-10]两大类.自适应误差扩散算法在一定程度上改善了半色调输出结果,但由于自适应误差滤波器系数的获取存在一定的滞后性以及计算复杂度较高等原因,限制了其进一步发展.基于色调的变系数误差扩散算法对色调还原性好,运算效率高,是目前研究的热点.
为避免现有误差扩散算法存在的人工结构和保证清晰纹理的再现,文中提出了一种将噪声调制与纹理结构相结合的阈值模型;为了能够更好地还原图像的色调以及保证输出图像的蓝噪声特性[11-13],文中利用蚁群算法对各灰度级下的最优误差扩散系数进行搜索,从而得到能根据图像灰度自适应调整误差过滤器系数的误差扩散算法.
1 经典误差扩散算法
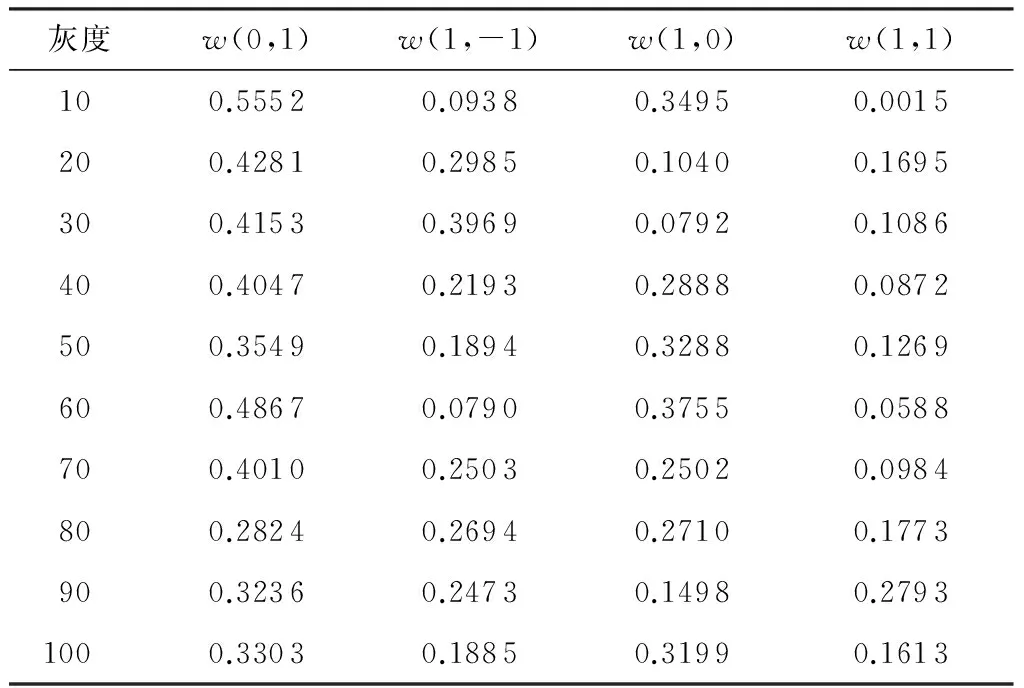
误差扩散算法的主要思想是:当前处理像素灰度等级与阈值比较得到的差值不应该仅由该像素承担,应分配给邻域像素.其算法流程如图1所示.其中f(m,n)为原始灰度图像,b(m,n)为输出的二值图像,Q[ ]为阈值模型,u(m,n)为经误差扩散后的输入图像,e(m,n)为输入图像与输出图像的差值, w(k,l)为误差扩散过滤器.常见的误差过滤器w(k,l)如图2所示,其中w(0,1)=7/16,w(1,-1)=3/16, w(1,0)=3/16,w(1,1)=1/16.

图1误差扩散算法流程图
Fig.1Flowchartoferrordiffusionalgorithm
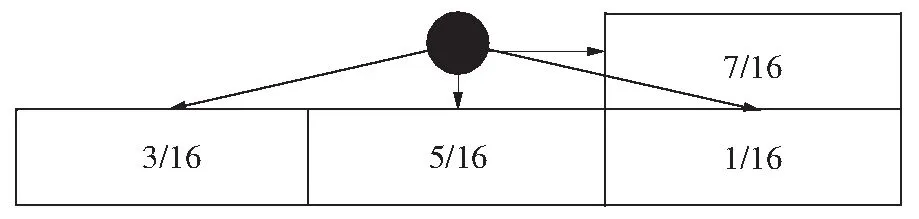
图2误差扩散过滤器示例
Fig.2Anexampleoferrordiffusionfilter
2 阈值模型设计
通常一幅图像既存在灰度均匀的平坦区,也存在灰度突变的纹理区.一般因误差扩散算法而产生的人工结构主要出现在平坦区,采用噪声调制的方法对误差扩散算法的阈值模型进行修正,可以在一定程度上减少人工结构.文中使用白噪声随机数发生器Nr来构造阈值函数进行阈值调制,具体的阈值模型如下:
(1)
其中T为分界阈值,取值为0.5.经过噪声调制后的误差扩散算法,在一定程度上减少了人工结构,但也会带来细节模糊化的影响,降低输出图像的质量.人工结构的产生,主要集中在图像灰度均匀的区域,因此无须对整幅图像进行噪声调制.文中提出的基于噪声调制与纹理结构的阈值模型在图像的平坦区进行噪声调制,以消除非期望的人工结构,而在图像的纹理区利用图像的局部纹理信息对图像进行阈值调制,以保证输出图像的纹理再现.
文中是在图像局部纹理信息[14-15]的基础上进行改进,得到了纹理增强反馈阈值模型.对于一个3×3的局部图像区域,首先计算该区域的平均灰度:
(2)
其中P(i,j)为水平、垂直和对角线方向的权值,水平和垂直方向取0.146 5,对角线方向取0.103 5.文中根据V(m,n)的大小将图像分成3个区域:
(1)平坦区.当局部视觉偏差V(m,n)≤Tv1时,当前局部区域被视为平坦区,采用噪声调制的阈值模型.其中Tv1为平坦区与轻度纹理区的分界阈值,经测试分析发现,该阈值在(0.005,0.010)之间取值时,实验效果较为理想.
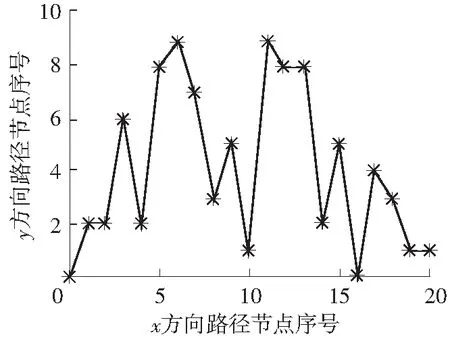
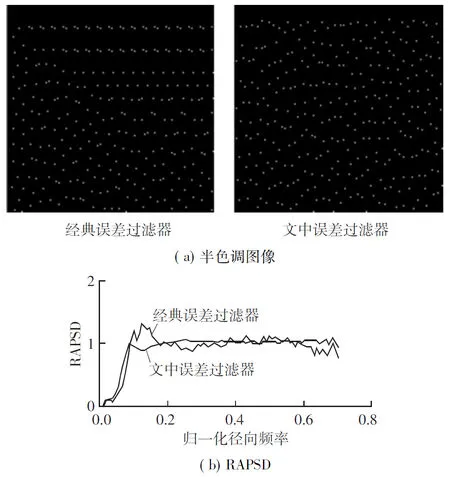
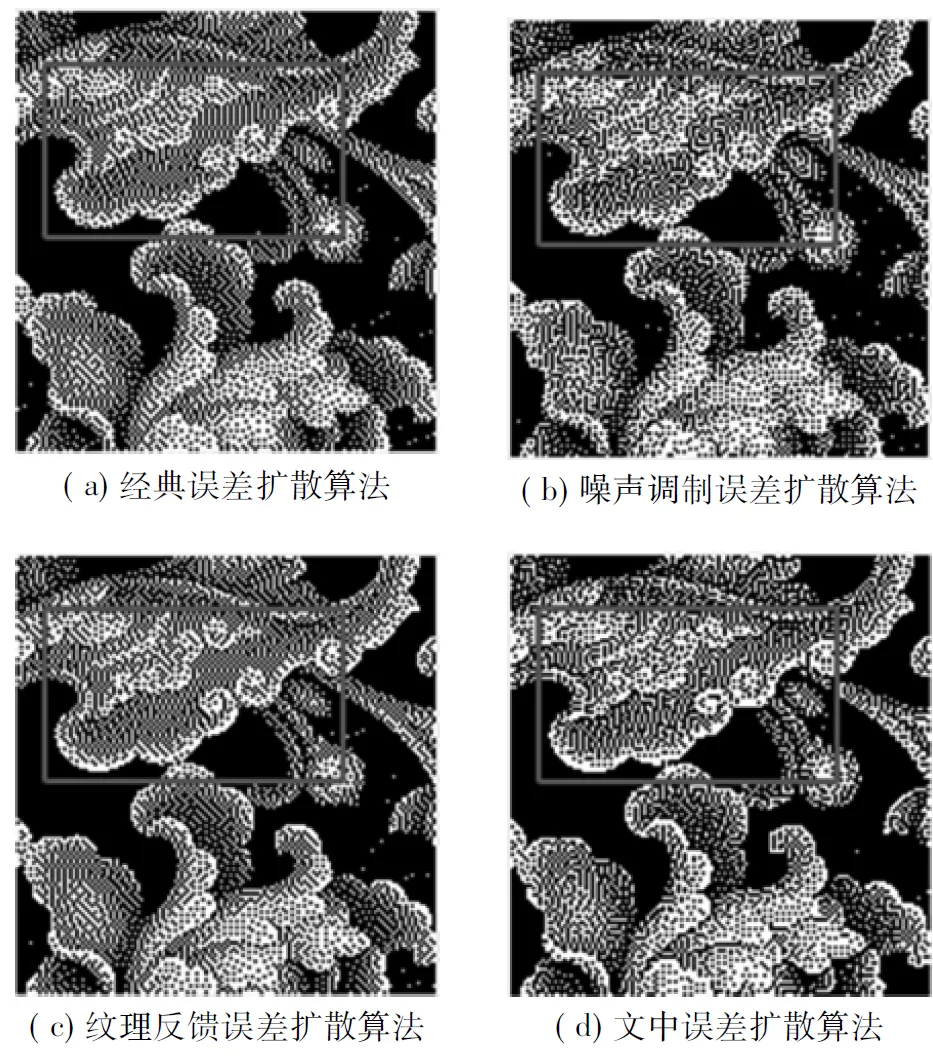
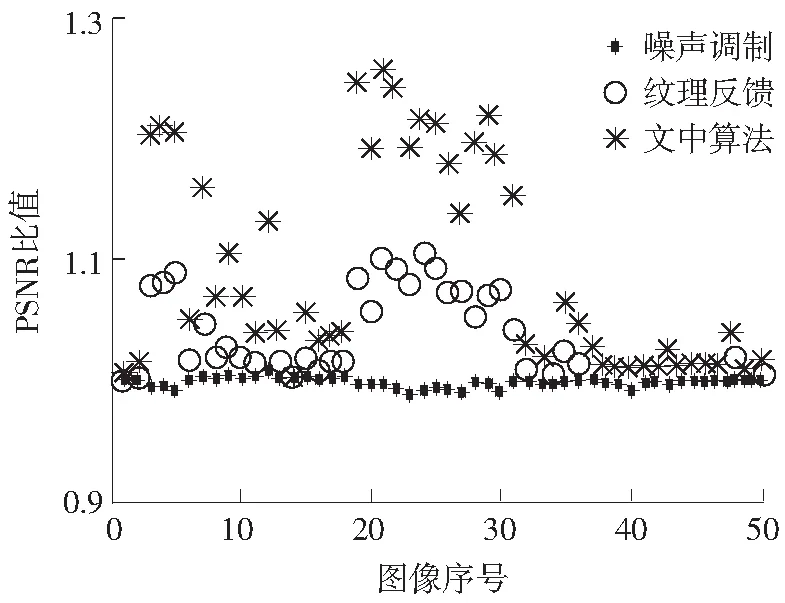
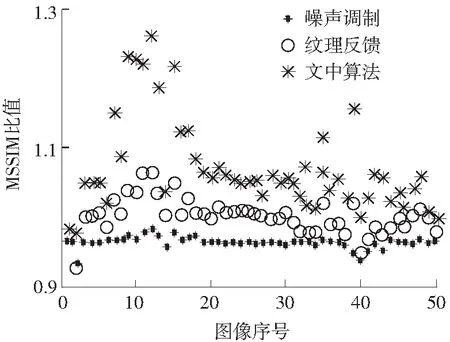
(2)轻度纹理区.当局部视觉偏差满足Tv1 (4) (3)高度纹理区.当局部视觉偏差V(m,n)>Tv2时,当前局部区域被视为高度纹理区,采用高度纹理反馈的阈值模型.高度纹理区的反馈信息为 H(m,n)=S(m,n)+βD(m,n) (5) (6) 对不同的灰度级采用相同的误差扩散系数,其输出结果存在着明显的差异.寻求各个灰度级下最合适的误差扩散系数,对改善输出半色调图像的质量,提高输出图像的视觉效果有着重要的作用.蚁群算法是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法,有分布式计算、信息正反馈和概率搜索的特点,该算法已广泛应用于优化问题,在某些情况下具有比神经元网络和遗传算法更好的搜索性[16].分布式计算使算法可以并行运行,大大提高运行效率.信息正反馈使得在较优的路径上留下更多的信息素,吸引更多的蚂蚁,引导整个系统向最优化方向进化.概率搜索增加了生成解的随机性,在一定程度上避免了陷入局部最优解.因此,蚁群算法在提高运行效率的同时,可以获取一定程度上的满意解.文中采用蚁群算法来搜索各灰度级下的最优误差扩散系数. 3.1适应度函数 对于适应度函数的建立,从图像的空间特性和频谱特性[17]两方面进行考虑.空间特性的评价指标: F1=1-l(x,y)c(x,y) (7) 频频特性的评价指标: (8) F=ηF1+(1-η)F2 (9) 式中,η表示F1与F2的相对重要关系,在(0,1)之间取值,文中取η=0.3,即频谱特性指标更加重要. 3.2蚁群算法优化过程 设误差扩散系数w(0,1)、w(1,-1)、w(1,0)、w(1,1)均有5位有效数字,小数点前一位和后4位,则蚂蚁在某次循环的节点和路径如图3所示. 图3蚂蚁路径图 Fig.3Track of an ant 每只蚂蚁从原点出发,依次经过20个节点到达目的地.其中节点1-5的纵坐标对应w(0,1)的5位有效数字,节点6-10的纵坐标对应w(1,-1)的5位有效数字,节点11-15的纵坐标对应w(1,0)的5位有效数字,节点16-20的纵坐标对应w(1,1)的5位有效数字. 蚁群算法的具体流程如下: (1)初始化误差扩散系数,以经典误差扩散算法的扩散系数作为初始值,设定初始路径,确定种群规模M=50,迭代次数K=100,当前迭代次数k=1,起点pathi=0; (2)pathi=pathi+1,根据当前环境留下的信息素以及该蚂蚁的能见度ρ,计算出各蚂蚁移动到节点pathi的概率,并根据赌轮盘的方法进行概率搜索,为每只蚂蚁选择节点pathi的位置; (3)若pathi=20,则转步骤(4),否则转步骤(2); (4)根据式(9)计算所有蚂蚁的适应度函数,并更新当前环境的信息素,k=k+1; (5)若k≤100,则转步骤(2),否则搜索结束,将最后一代中适应度函数值最小的蚂蚁路径作为最优误差扩散系数. 表1 基于色调的误差扩散过滤器 通过蚁群算法获得的最优及次优误差扩散系数会影响半色调输出图像在频谱特性上接近蓝噪声的程度.为了尽可能获取各灰度级下最优的误差扩散系数,文中多次运行蚁群算法,并将其中最好的结果作为色调感知的变系数误差过滤器.为了验证该误差过滤器在半色调处理过程中可以产生更具蓝噪声特性的结果图像,文中对灰度级为4/255的均匀灰度图像,采用经典误差过滤器和文中得到的误差过滤器分别进行误差扩散处理,并计算相应的RAPSD(径向平均功率谱密度),结果如图4所示. 图4两种误差过滤器的输出结果对比 Fig.4Comparison of output results between two error diffusion filters 从图中可以看出,基于色调的误差扩散系数所得到的半色调图像中,点的分布相对均匀,在低频处具有陡峭的截止频率响应特性,在高频处有类似白噪声的平坦频谱,因而更加接近蓝噪声特性. 4种算法对一幅既有平坦区又有纹理区的图像进行半色调处理,所生成的结果图像如图5所示. 图54种算法生成的半色调图像 Fig.5Halftone images by four algorithms 观察图5(a)中的方框区域,发现在灰度平坦区出现了竖直方向的条纹状人工结构,影响图像质量;从图5(b)可知,在灰度平坦区域,条纹状的人工结构消失,但因噪声的引入,图像变得模糊化,细节丢失严重;观察图5(c)中的方框区域,图像纹理较好,边缘清晰,但在部分低灰度的平坦区域出现了类似图5(a)中条纹状的人工结构;从图5(d)可知,图像的纹理清晰,边缘比图5(c)更为突出,同时也不存在条纹状的人工结构,具有良好的视觉效果. 为定量评价4种算法的半色调输出效果,表2列出了4种算法的信噪比(PSNR)和结构相似度(MSSIM).一般信噪比越大,半色调图像越接近原始图像的品质,从4种算法的信噪比可知,文中算法比其他3种算法具有更高的信噪比.结构相似度是用来衡量半色调图像与原图像之间的结构信息的保留程度,该值越大,表明半色调图像的结构保留程度越好.从4种算法的结构相似度可知,文中算法对原图像的结构信息保留最好. 表24种算法的PSNR 和 MSSIM比较 Table 2Comparison of PSNR and MSSIM among four algorithms 算法PSNRMSSIM经典误差扩散算法6.23490.5137阈值调制误差扩散算法6.21360.5122纹理反馈误差扩散算法6.36630.5236文中误差扩散算法6.41960.5276 为进一步验证中文算法的通用性,对美国南加州大学的USI-SIPI 图像数据库中的50幅图像分别采用4种算法进行半色调处理,并计算出3种算法(阈值调制误差扩散算法、纹理反馈误差扩散算法、文中误差扩散算法)的PSNR和MSSIM与经典误差扩散算法的PSNR和MSSIM的比值,结果见图6. (a)PSNR比值 (b)MSSIM比值 从图中可以看出,噪声调制误差扩散算法的性能指标总体上维持在经典算法附近,纹理反馈误差扩散算法的性能指标明显高于经典误差扩散算法,而文中误差扩散算法的性能指标又高于纹理反馈误差扩散算法.因此,文中算法的PSNR和MSSIM均高于其他3种算法,具有一定的通用性. 文中提出了一种基于纹理与色调感知的变系数误差扩散算法.根据图像的局部视觉偏差将图像分为平坦区、轻度纹理区和高度纹理区.在平坦区,采用噪声调制的方法来减少误差扩散算法中出现的人工结构;在纹理区,根据纹理程度的不同采用不同的反馈因子,以保证输出图像的纹理结构.为了获取基于色调的变系数误差过滤器,先建立一个既考虑图像空间特性又考虑图像频谱特性的综合指标,然后利用蚁群算法搜索出具有良好蓝噪声特性的自适应误差扩散系数,并对灰度级为4/255的图像进行半色调处理,实验结果表明,利用蚁群算法获得的基于色调感知的误差过滤器,输出的半色调图像均匀性好,且更具蓝噪声特性.文中算法与经典误差扩散算法、噪声调制误差扩散算法及纹理反馈误差扩散算法的对比实验结果表明,文中算法输出的半色调图像既减少了人工结构,又保证了纹理结构的再现,具有较好的视觉效果. [1]梁永锋.一种改进的误差扩散算法 [D].西安:西安电子科技大学,2013:1-2. [2]姚海根,程鹏飞.数字半色调技术 [M].北京:印刷工业出版社,2013:139. [3]CHANDUK,STANICHM,WUCW,etal.Directmulti-bitsearch(DMS)screenalgorithm[C]∥Proceedingsofthe19thIEEEInternationalConferenceonImageProce-ssing.LosAlamitos:IEEE,2012:817-820. [4]FLOYDR,STEINBERGL.Anadaptivealgorithmforspatialgrayscale[J].JournaloftheSocietyforInformationDisplay,1976,17(2):75-77. [5]孙虹.半色调纹理优化方法 [D].西安:西安电子科技大学,2014:29-37. [6]WUHuisi,WONGTien-Tsin,HENGPheng-Ann.Parallelstructure-awarehalftoning[J].MultimediaToolsandApp-lications,2013,67(3):529-547. [7]DAMERA-VENKATAN,EVANSBL.Adaptivethresholdmodulationforerrordiffusionhalftoning[J].IEEETransactionsonImageProcessing,2001,10(1):104-116. [8]CHUNGK-L,PEIS-C,PANY-L,etal.Agradient-basedadaptiveerrordiffusionmethodwithedgeenhancement[J].ExpertSystemswithApplications,2011,38(3):1591-1601. [9]LIP,ALLEBACHJP.Tone-dependenterrordiffusion[J].IEEETransactionsonImageProcessing,2004,13(2):201-215. [10]胡建华,王云宽,王慎航,等.自适应噪声调制多级误差扩散算法 [J].计算机辅助设计与图像学报,2014,26(11):1974-1980. HUJian-hua,WANGYun-kuan,WANGShen-hang,etal.Anadaptivenoisemodulationmultilevelerrordiffusionalgorithm[J].JournalofComputer-AidedDesign&ComputerGraphic,2014,26(11):1974-1980. [11]ULICHNEYRA.Ditheringwithbluenoise[J].ProceedingsoftheIEEE,1988,76(1):56-79. [12]BACCARodriguezJ,ARCEGR,LAUDL.Blue-noisemultitonedithering[J].IEEETransactionsonImageProcessing,2008,17(8):1368-1382. [13]FUNGYik-Hing,CHANYuk-Hee.Optimizingtheerrordiffusionfilterforbluenoisehalftoningwithmultiscaleerrordiffusion[J].IEEETransactionsonImageProcessing,2013,22(1):413-417. [14]KWAKNae-Joung,RYUSoung-Pil,AHNJae-Hyeong.Edge-enhancederrordiffusionhalftoningusinghumanvisualproperties[J].HybridInformationTechnology,2006,1:499-504. [15]章芳,庞明勇.一种呈现清晰纹理的快速误差扩散算法 [J].小型微型计算机系统,2010,31(8):1609-1612. ZHANGFang,PANGMing-yong.Structure-awareandhigh-speederrordiffusionalgorithm[J].JournalofChineseComputerSystems,2010,31(8):1609-1612. [16]马良,朱刚,宁爱兵.蚁群优化算法 [M].北京:科学出版社,2010:15-24. [17]LIULing-yue,CHENWei.Animprovedparallelcontrast-awarehalftoning[J].JournalofZhejiangUniversity-Science(Computer&Electronics),2013,14(12):918-929. SupportedbytheNationalNaturalScienceFoundationofChina(61273280) AnErrorDiffusionAlgorithmwithVariableCoefficientsBasedonTextureStructureandToneAwareness WANG Xin-boHU Jian-huaWANG Yun-kuanWU Shao-hongLU Hao (InstituteofAutomation,ChineseAcademyofScience,Beijing100190,China) Thetraditionalerrordiffusionalgorithmmaycauseunexpectedartifactstoproduceanditcan’tpresentthedetailsverywell.Inordertosolvetheseproblems,anerrordiffusionalgorithmwithvariablecoefficientsisproposedonthebasisoftexturestructureandtoneawareness.Inthealgorithm,first,accordingtolocalvisualerrorsofanimage,thethresholdismodifiedbyperformingthenoisemodulationinsmoothregionsandbyutilizingthetextureinformationintexturedregions.Then,bytakingintoconsiderationthespectralcharacteristicofbluenoiseandthespatialcharacteristicoftheimage,theadaptiveerrordiffusioncoefficientsateachgraylevelareobtainedbyusingtheantcolonyalgorithm.Experimentalresultsshowthattheproposedalgorithmcanoutputhalftoneimagestoreducetheunexpectedartifactsandcanensurethedetailsoftexturestructure,andthatithasabetterperformanceintermsofPSNRandMSSIM. errordiffusion;imagetexture;noisemodulation;antcolonyoptimization 1000-565X(2016)09-0041-06 2016-02-21 国家自然科学基金资助项目(61273280);中国科学院先导科技专项(XDA09020302) 王欣波(1988-),男,博士生,主要从事数字印刷、图像处理研究.E-mail:xinbo.wang@ia.ac.cn TP391.8 10.3969/j.issn.1000-565X.2016.09.006
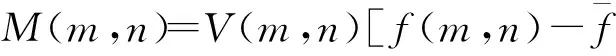
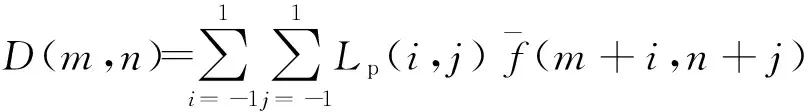
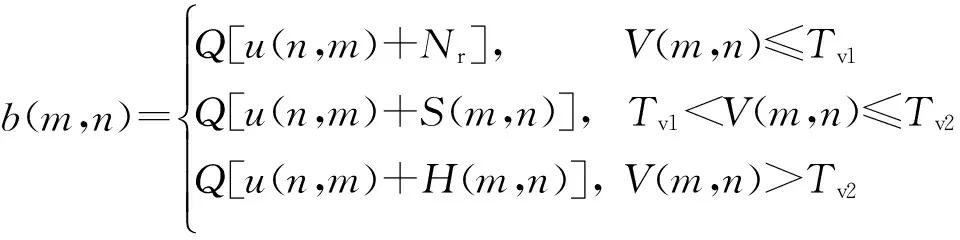
3 误差过滤器设计

4 实验结果与分析

5 结论

