一种改进的移动机器人三维路径规划方法*

吴玉香　王超

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)



一种改进的移动机器人三维路径规划方法*

吴玉香王超

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)

针对工作环境已知的情况，研究了移动机器人的全局三维路径规划问题.首先改进蚁群算法全局信息素的更新策略和信息素增量的计算方法，使规划出的路径效果更优；接着引入安全性因素并提前离线计算，设计当蚂蚁陷入死锁时将该点信息素清零的回退机制，以实现复杂三维环境中机器人的高效避障；然后对传统搜索模式进行改进，实现机器人垂直于前进主方向的移动方式.仿真结果表明，采用文中设计的路径规划方法得到的三维路径长度短，搜索效率高，且更加符合实际情况.

路径规划；三维空间；移动机器人；蚁群算法

路径规划是移动机器人导航研究中最重要的内容之一，也是移动机器人能够安全可靠地执行各项任务的基本保障[1].目前，在移动机器人路径规划的研究中，使用较多的算法主要有遗传算法[2-3]、人工势场法[4-5]、粒子群优化算法[6-7]等.对于复杂的、制约多的三维环境，上述算法都有一定的局限性，例如遗传算法的单一编码不能全面地表达环境约束，对于规模较大的三维路径规划问题很难规划出较优的路径；人工势场法容易出现终点不可到达的问题；粒子群优化算法的全局搜索能力不足，受三维环境的复杂约束的影响大.针对三维环境复杂的地貌特征给机器人路径规划带来的挑战，文献[8-10]提出了一些新的算法，但这些算法存在复杂、搜索空间大的缺点.蚁群算法作为一种新兴的启发式优化算法，已成功应用于旅行商[11]、二维路径规划[12]等复杂问题的求解.相比前面几种算法，蚁群算法的搜索机制是随机的，且具有正反馈的特点，算法本身具有分布计算、群体智能等方面的优势[13-14]，这意味着在复杂三维环境的路径规划过程中，蚁群算法的全局搜索能力更强，可以更方便地表达环境约束，实现过程简单.但蚁群算法也存在一些局限性，针对算法易陷入局部最优、收敛速度慢的缺点，文献[15]将蚁群算法的搜索分为两个阶段，有效地平衡了路径规划的效果和算法运行效率；文献[16]提出了一种新的信息素更新方法，根据学习次数和与最近障碍物的距离来调节信息素，能够快速找到理想路径；针对蚂蚁易陷入死锁的缺点，文献[17]引入了带方向信息的全局启发因子，并通过惩罚函数和死亡机制来解除死锁，能够在较短的时间内规划出满足条件的最优路径，但这种方法空间开销较大.文中针对三维环境的复杂特点和蚁群算法的缺点，对搜索模式以及蚁群算法提出了新的改进算法，并将其应用到移动机器人的三维路径规划中，最后通过仿真实验验证该算法的有效性和正确性

1　三维环境建模

环境建模是移动机器人路径规划第1步需要完成的工作，模型建立的好坏直接影响到路径规划的效果.文中借鉴对三维空间进行栅格化的方法[18]进行环境建模.为了方便后续工作的进行以及提高路径规划的效率，在进行栅格化之前，需要对机器人工作空间做一些特殊化处理.首先，针对机器人的越障能力，将低于机器人越障高度的障碍物直接去除.其次，对于机器人所不能越过的障碍物，根据机器人的安全移动半径对其进行相应的膨化处理.接下来对特殊化处理的工作空间进行栅格化，如图1(a)所示.首先建立三维直角坐标系O-XYZ，再在坐标系中构造一个立体区域ABCD-EFGH，其中ABCD平面在XOZ平面上.然后将机器人的工作空间置于该立体区域，AB、AE分别等于机器人工作空间的长度和宽度.

得到规划空间后，就可以进行进一步划分.首先，沿Y轴对ABCD-EFGH进行n等分，得到n+1个平面.然后对任意平面沿Z轴进行l等分，沿X轴进行m等分，如图1(b)所示.这样规划空间就被离散为n×m×l个栅格.在实际应用中，栅格大小的划分应以机器人能在单位栅格内自由运动为前提，也就是说应据此来选取n和m，l为高度上的划分，文中根据机器人爬坡能力来确定，这样可以较好地兼顾环境信息存储量和路径规划的精度.

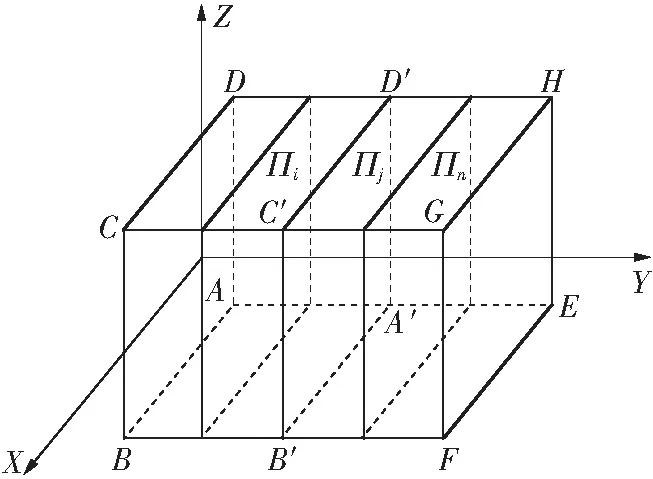
(a)规划空间的划分

(b)任意平面的划分

Fig.1Schematic diagrams of division of planning space and arbitrary plane

经过以上处理，机器人的工作空间就可以用离散点的集合来表示，记为S*.S*中的任意点都可以用序号坐标来表示，i、j、k分别对应于p点沿X、Y、Z轴方向的划分序号.

2　三维路径规划

2.1信息素表示及更新

在蚁群算法中，信息素是蚁群在觅食过程中对蚂蚁产生吸引作用的信息载体，在一定程度上其对算法的收敛速度和路径规划效果有着十分重要的影响，信息素更新分为局部信息素更新和全局信息素更新.文中采用环境模型中的离散点作为信息素的载体.

局部信息素更新是指蚂蚁每经过一个离散点时，都将立刻减少该离散点的信息素浓度.其目的是减少其他蚂蚁选择该点的可能性，增加选择未访问过的点的概率.其更新规则如下：

(1)

全局信息素更新是指蚁群算法在完成一次循环计算后，以每只蚂蚁搜索到的路径长度作为评价值，然后从路径集合中选择最优路径，对该路径上各离散点的信息素进行更新，其更新规则如下：

(2)

(3)

式中，L(a)为第a只蚂蚁所走过的路径长度，K为常数，ρ为信息素更新系数.

但这种方式容易导致算法陷入局部最优解.为此，文中提出了一种新的全局信息素更新策略，不仅对已搜索到的最优路径上的信息素进行更新，同时在当前循环最优路径和已搜索的最优路径长度不相等的情况下，也对当前循环最优路径上的信息素进行更新.另外，当算法处于停滞状态达到一定的循环次数时，停止对已搜索最优路径上的信息素进行更新，使蚂蚁的搜索从有序趋于无序，避免已搜索最优路径上的信息素浓度过高，从而增大算法发现更优解的能力.

(4)

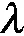
2.2启发式函数设计

启发式函数设计的目的是利用启发信息引导机器人从起点寻找到终点的路径.在路径规划过程中，机器人应尽量远离障碍物.为此，文中引入了离散点的安全性因素[19]，其计算公式如下：

(5)

式中，N1(i，j，k)为点(i，j，k)的可视区域内离散点的数量，N2(i，j，k)表示点(i，j，k)的可视区域内不可行点的数量.此时，算法的启发式函数设计为

H(i，j，k)=Rw1(i，j，k)Qw2(i，j，k)Sw3(i，j，k)

(6)

R(i，j，k)为当前点到下一点的路径长度的倒数，

(7)

(ia，ja，ka)为下一点的坐标；Q(i，j，k)为下一点到目标点距离的倒数，

(8)

(ib，jb，kb)为目标点的坐标；w1、w2、w3为系数，取值范围是(0，1]，其值越小，表明对应因素的重要程度越高.

文中在引入安全性因素的同时也带来了一个巨大的弊端，即算法的复杂度大大增加，蚂蚁在搜索下一个可行点时，由于要计算可视域内每个离散点的安全性因素，也就是对备选离散点的可视区域也要进行扫描.因此，文中提出的改进算法是将安全性因素的计算从路径规划的过程中抽离出来，在环境建模阶段就提前离线计算好规划空间内每个离散点的安全值，在路径规划过程中只需调取相应点的安全值即可.

2.3死锁解除

在基于蚁群算法的机器人路径规划过程中，蚂蚁在搜索路径时经常陷入凹形障碍物，这种现象称为“死锁”.如果对死锁现象没有采取合理的处理方式，那么该蚂蚁将会处于死亡状态，算法运行过程将会因出现错误而中断.在二维平面的路径规划中，通常的做法是在环境建模阶段将此类凹形障碍物做填补处理.而在三维空间的路径规划中，由于地形环境和障碍物的复杂性，这种对陷阱进行填补处理的方式是行不通的.为此，文中提出了一种相对简单易行的方法，以有效避免蚂蚁陷入死锁.若蚂蚁在探索路径的过程中掉入陷阱，且没有任何可行点可供选择时，蚂蚁退回上一步所在的点，并将当前点的信息素设置为0，那么当前点就会变为不可行点，蚂蚁再次重新选择，如依然没有可行点，再回退一步，依此类推，直至蚂蚁逃离陷阱.这样并不需要提前知晓陷阱障碍物的信息，只要有一只蚂蚁有一次掉入陷阱并且退出了，那么该陷阱就相当于填平了，不会再有第二只蚂蚁掉入该陷阱.这种方法应用起来比较容易，死锁现象的解除效率也相对较高.

2.4搜索模式

三维路径规划中经常使用逐个平面搜索和可视域相结合的方式作为蚂蚁的搜索模式，取X轴方向作为机器人三维路径规划的主方向.设机器人的起点为pS，终点为pG.蚂蚁以X轴为主方向前进，并规定机器人在前向运动单位栅格的情况下，允许机器人最大横向运动栅格数为ymax，最大纵向移动栅格数为hmax.也就是说，蚂蚁此时对下一个点的搜索存在一个可视区域.蚂蚁构建路径的过程如图2所示.

图2　路径选取过程

首先蚂蚁从起点pS出发到达第1个平面上的一个可行点p1(i1，j1，k1)，接着由p1出发选择第2个平面∏2的可视区域内的下一个点p2(i2，j2，k2)，各点的选择概率计算式如下：

(9)

如果此蚂蚁依次在接下来的各个平面中选择路径点，则可寻找到一条完整的路径.

这种方式比较简单易行，路径规划的效果和算法的运行效率都比较满意.但此种方法的弊端是机器人不能在与机器人前进主方向垂直的方向上移动.这是不符合实际应用的，并且在复杂环境中这样搜索出来的路径也可能不是最优的.

为此，文中提出了一种新的搜索模式，如图3所示，当机器人处于图中心的栅格，且机器人纵向允许的最大移动栅格为1时，其候选栅格为机器人下一个平面的9个栅格和机器人自身所在平面其左右两列的6个栅格，共15个候选栅格.之所以没有考虑机器人上一平面的栅格，是因为机器人在寻找到目标点的路径过程中很少遇到需要后退的情况，并且文中针对死锁现象已引入了回退机制，这样足以应付绝大多数的工作环境，减少机器人在搜寻路径的过程中很多不必要的浪费.

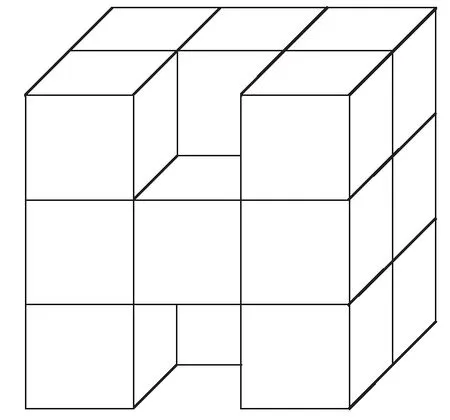
图3　改进的搜索模式

文中的路径规划方法是在蚁群算法的基础上根据复杂三维环境的特点而提出的，算法的收敛性分析和证明与文献[20]类同.

3　仿真实验与结果分析

为验证文中算法的性能与搜索模式的可行性，文中在同一计算机上采用Matlab R2012a软件进行仿真，计算机的CPU型号为Intel酷睿i3 2330M，内存为4 GB.对于机器人的路径规划空间，其实际大小为40 m×40 m×20 m，栅格划分为40×40×40，蚂蚁的数量为20，算法的循环次数为200，α=1，β=1，ρ=0.2，ξ=0.2.

3.1信息素更新策略改进前后对比实验

在本次实验中，没有加入安全性因素和死锁检测机制，所以为了尽量避免因蚂蚁陷入死锁而导致程序运行过程出现错误，假设机器人爬坡能力较强，允许蚂蚁最大纵向的移动栅格数hmax=3.环境模型及高度与灰度的关系示意图如图4所示.

图4　环境模型及高度与灰度的关系示意图

Fig.4Environment model and schematic diagram of the relationship between height and grey

在所有参数和设置相同的情况下，使用基本蚁群算法和文中基于改进信息素更新策略的蚁群算法进行三维空间路径规划，其路径规划效果和路径变化趋势如图5所示.从图5(a)可以看出，文中算法的寻优效果比基本蚁群算法有了较大的提高.从图5(b)可以看出，当文中算法停滞一定次数没有寻找到更优解时，由于已寻找的最优路径上的信息素停止更新，并且经过上一轮规划后，最优路径上的信息素已经大量挥发，其对蚂蚁的吸引程度极大减弱，蚂蚁立即从有序变为无序，导致规划的路径平均长度有所激增，然后在更优路径上潜在点的信息素得到逐渐增加，从而使平均路径长度迅速减小，并且通常还可能寻找到更优的路径.

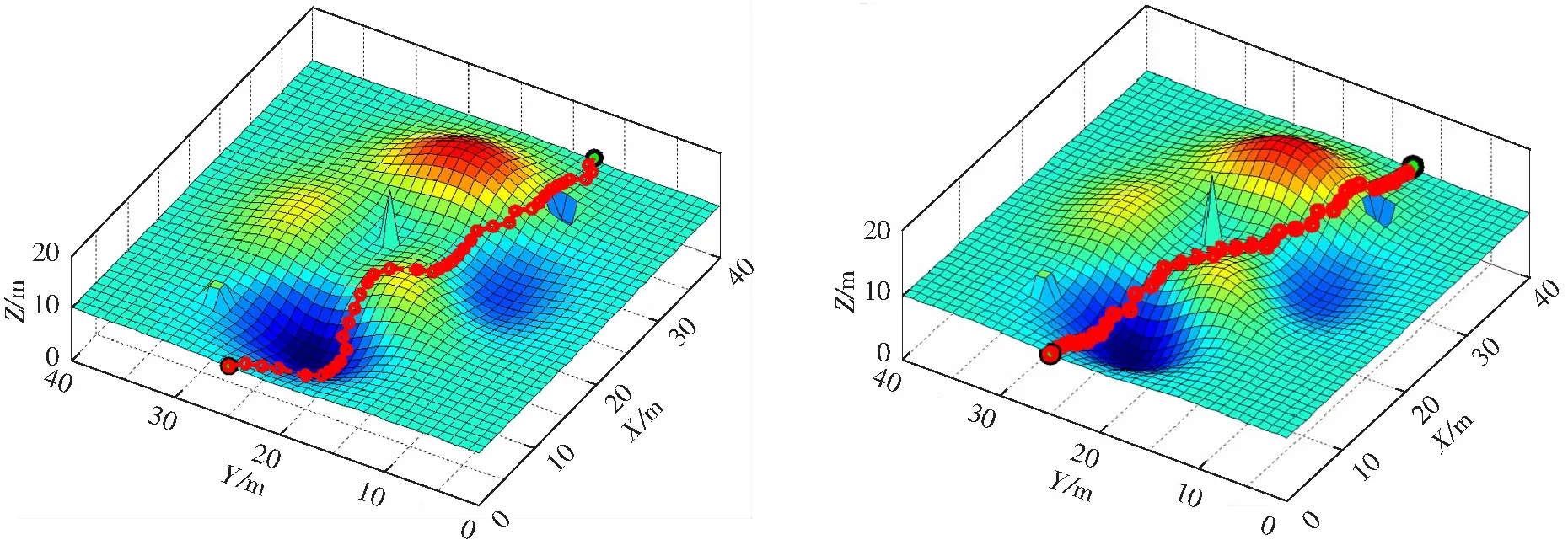
基本蚁群算法文中改进蚁群算法

(a)三维路径规划效果

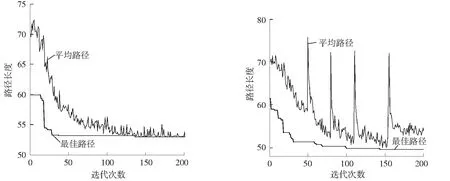
基本蚁群算法文中改进蚁群算法

(b)路径变化趋势

图5两种蚁群算法的三维路径规划仿真结果

Fig.5Simulation results of 3D path planning by two ant colony algorithms

对信息素更新策略改进前、后的蚁群算法进行多次仿真实验.文中引入评价蚁群算法性能的3个基本指标[21].定义最佳性能指标EO如下：

(10)

式中：cb为算法经过很多次运行之后所得到的最优值；c*为所要求解问题的理论最优值，如果理论最优值未知，可以用已知的最优值来替代.最佳性能指标用以衡量蚁群算法对问题的最佳优化度，其值越小意味着蚁群算法的优化性能越好.

定义时间性能指标ET如下：

(11)

式中，Ia为算法从开始运行到终止时迭代次数的平均值，t为算法在完成一次迭代后所要消耗的运算时间.时间性能指标用以衡量蚁群算法搜索问题解的快慢程度，在Imax固定的前提下，其值越小说明蚁群算法的收敛速度越快.

定义蚁群算法的鲁棒性性能指标ER如下：

(12)

式中，ca为经过多次运行之后算法所得到的所有数据的平均值.鲁棒性能指标用以反映蚁群算法对操作以及随机初值的依赖程度.

在相同条件下分别使用信息素更新策略改进前、后的蚁群算法进行多次实验，随机各抽取3组结果，如表1所示.

表1　实验测试结果

计算得到信息素更新策略改进前、后蚁群算法的3项性能指标，如表2所示.由表中可知，信息素更新策略改进后蚁群算法的寻优能力和鲁棒性得到了有效增强，算法的收敛速度也相对越快.

表2蚁群算法改进前、后的性能对比

Table 2Comparison of ant colony algorithm performance before and after improvement%

算法EOETER改进前10.2591.6410.42改进后0.8474.242.11

3.2引入安全性因素的时间对比实验

在所有参数和设置相同的情况下采用传统方法(在路径规划过程中进行安全性因素的计算和扫描)及文中算法(在环境建模阶段就计算好所有离散点的安全性因素，路径规划时只需要按需调用)进行实验.两种算法的运行时间如表3所示.

表3两种算法的运行时间

Table 3Running time of two algorithmss

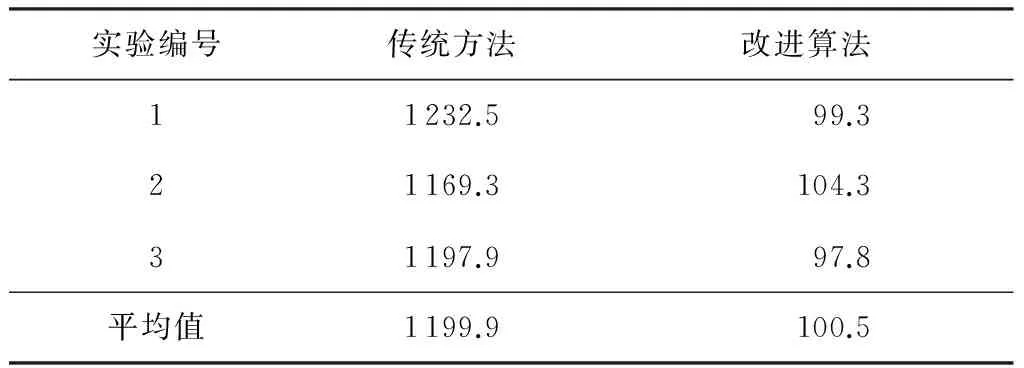
实验编号传统方法改进算法11232.599.321169.3104.331197.997.8平均值1199.9100.5

由表中可知，在环境建模阶段提前计算好规划空间内所有离散点的安全性因素，算法的运行时间相比传统方法大为缩短，由此证实这种方法是有效的、可行的，其在实际应用中的意义是不言而喻的.

3.3改进信息素更新策略、引入安全性因素和回退机制的实验

文中针对基本蚁群算法改进了信息素的更新策略，引入了安全因素并提前离线计算好安全性因素，针对死锁的检测和解除引入了回退机制并加以改进.本实验综合以上改进措施，为验证其可行性，限制了机器人的爬坡能力，将其纵向允许移动的最大栅格数hmax设置为1.实验结果如图6所示.由图可知，针对三维空间的复杂性和蚁群算法的缺点，经过一系列改进后的算法是可行的，该算法能够有效地避开障碍物以及对死锁现象进行检测和解除，并且算法最终可以搜索到一条相对较优的路径，路径规划效果和效率比基本蚁群算法有了较大的提高.

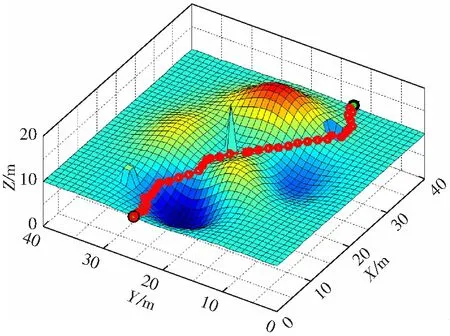
(a)路径规划效果

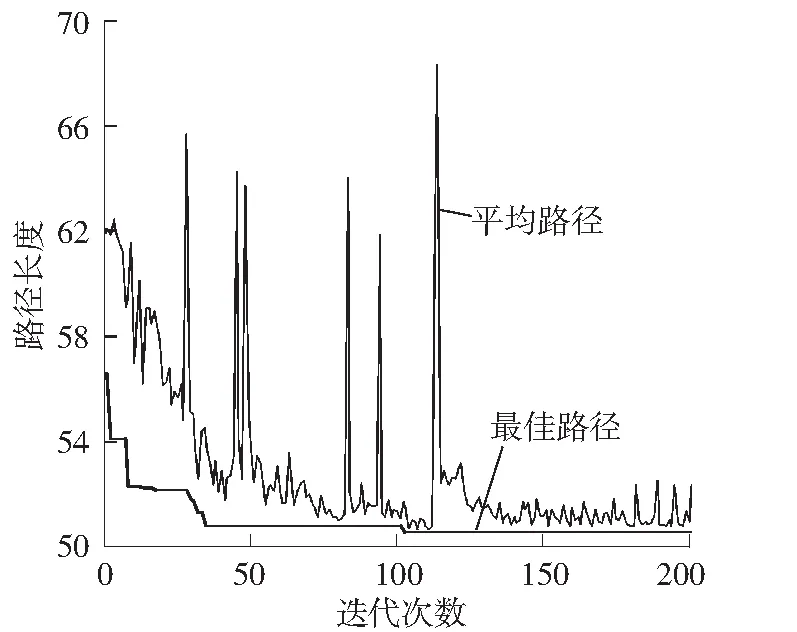
(b)路径变化趋势

Fig.6Simulation result of 3D path planning after a series of improvements

3.4搜索模式改进的实验

本实验是在基于改进算法的基础上进行的.首先对机器人的工作空间进行环境建模，并按照文中提出的搜索模式计算规划空间内各离散点的安全性；然后初始化各项参数，确定机器人的起始点和目标点，当蚂蚁处于当前离散点时，按照文中提出的搜索模式计算各候选离散点的选择概率，使用轮盘赌法选择下一个离散点.传统搜索模式与改进搜索模式的路径规划效果俯视图如图7所示.由图7(b)中的椭圆圈处可知，机器人在搜索路径的过程中可以实现在与主方向垂直的方向上移动，且路径规划的效果较优.采用文中的搜索模式规划出来的路径更加符合实际应用情况.

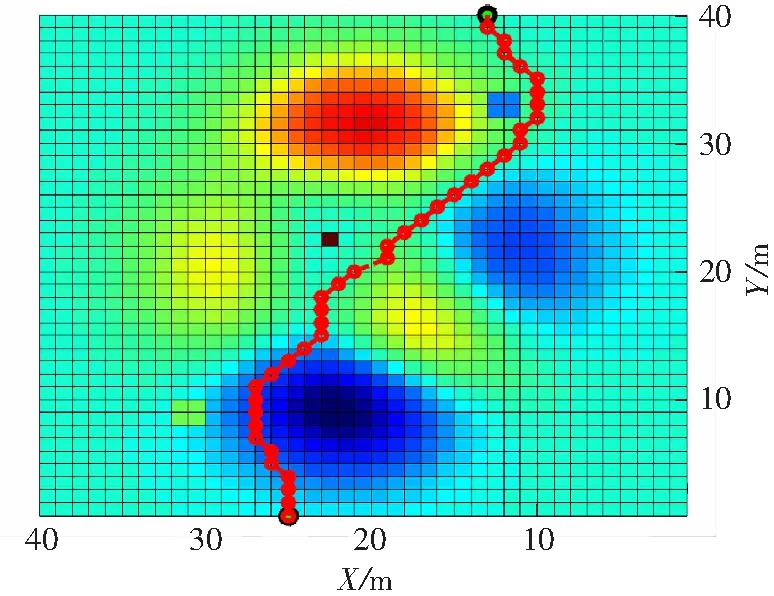
(a)传统搜索模式

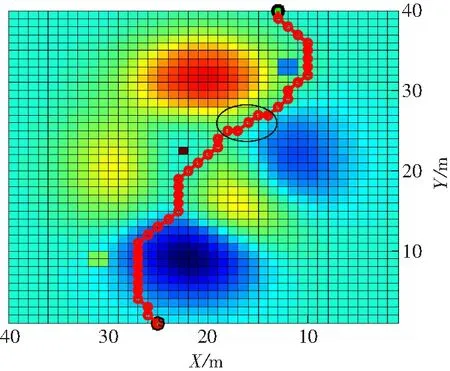
(b)改进搜索模式

图7两种搜索模式的路径规划效果俯视图

Fig.7Top views of path planning effect by two search modes

4　结论

文中采用蚁群算法对机器人在已知三维工作环境下的全局路径规划问题进行研究，采用栅格化的方法对机器人的工作空间进行三维建模，改进了信息素增量的计算方式，并采用了已搜索最优路径和当前循环最优路径信息素更新相结合的方式，以提高算法的收敛速度和路径寻优能力.启发式函数设计中引入了安全性因素，并提前离线扫描计算，提出了当蚂蚁陷入死锁时将该点的信息素清0的回退机制，以实现复杂三维环境中移动机器人的高效避障和死锁解除.仿真实验结果表明，文中提出的搜索模式是可行的，规划的路径长度短且更加符合实际应用情况.

[1]DEEPAK B L，PARHI D R，KUNDU S.Innate immune based path planner of an autonomous mobile robot [J].Procedia Engineering，2012，38(1)：2663-2671.

[2]王雪松，高阳，程玉虎，等.知识引导遗传算法实现机器人路径规划 [J].控制与决策，2009，24(7)：1043-1049.

WANG Xue-song，GAO Yang，CHENG Yu-hu，et al.Knowledge-guided genetic algorithm for path planning of robot [J].Control and Decision，2009，24(7)：1043-1049.

[3]于海璁，陆锋.一种基于遗传算法的多模式多标准路径规划方法 [J].测绘学报，2014，43(1)：89-96.

YU Hai-cong，LU Feng.A multi-modal multi-criteria route planning method based on genetic algorithm [J].Acta Geodaetica et Cartographica Sinica，2014，43(1)：89-96.

[4]于振中，闫继宏，赵杰，等.改进人工势场法的移动机器人路径规划 [J].哈尔滨工业大学学报，2011，43(1)：50-55.

YU Zhen-zhong，YAN Ji-hong，ZHAO Jie，et al.Mobile robot path planning on improved artificial potential field method [J].Journal of Harbin Institute of Technology，2011，43(1)：50-55.

[5]LIU Z，YANG L，WANG J，et al.Soccer robot path planning based on evolutionary artificial field [J].Advanced Material Research，2012，562(8)：955-958.

[6]ATYABI A，PHON-AMNUAISYK S，HO C K.Navigating a robotic swarm in an uncharted 2D landscape [J].App-lied Soft Computing，2010，10(1)：149-169.

[7]温惠英，李俊辉，周玮明.适于车辆路径规划的改进型粒子群优化算法 [J].华南理工大学学报(自然科学版)，2009，37(7)：1-5.

WEN Hui-ying，LI Jun-hui，ZHOU Wei-ming.Improved particle swarm optimization algorithm for vehicle routing planning [J].Journal of South China University of Technology(Natural Science Edition)，2009，37(7)：1-5.

[8]朱大奇，孙兵，李利.基于生物启发模型的AUV三维自主路径规划与安全避障算法 [J].控制与决策，2015，30(5)：798-806.

ZHU Da-qi，SUN Bing，LI Li.Algorithm for AUV’s 3-D path planning and safe obstacle avoidance based on biological inspired model [J].Control and Decision，2015，30(5)：798-806.

[9]TODOR S，MARTIN M，HENRIK A，et al.Path planning in 3D environments using the normal distributions transform [C]∥Proceedings of IEEE International Conference on Intelligent Robots and Systems.Taipei：IEEE，2010：3263-3268.

[10]DAVID G，ERIEK D，GUY P，et al.Path planning based on fluid mechanics for mobile robots using unstructured terrain models [C]∥Proceedings of IEEE International Conference on Robotics and Automation.Anehorage：IEEE，2010：1978-1984.

[11]DORIGO M，GAMBARDELLA L M.Ant colony system：a cooperative learning approach to the traveling salesman problem [J].IEEE Transactions on Evolutionary Computation，1997，1(1)：53-66.

[12]朱庆保，张玉兰.基于栅格化的机器人路径规划蚁群算法 [J].机器人，2005，27(2)：132-136.

ZHU Qing-bao，ZHANG Yu-lan.An ant colony algorithm based on grid method for mobile robot path planning [J].Robot，2005，27(2)：132-136.

[13]吴孔江，曾永年，靳文凭，等.改进利用蚁群规则挖掘算法进行遥感影像分类 [J].测绘学报，2013，42(1)：59-66.

WU Kong-jiang，ZENG Yong-nian，JIN Wen-ping，et al.Remote sensing image classification based on improved ant-miner [J].Acta Geodaetica et Cartographica Sinica，2013，42(1)：59-66.

[14]ABDUL R B，WASEEM S，SALABAT K.Correlation as a heuristic for accurate and comprehensible ant colony optimization based classifiers [J].IEEE Transactions on Evolutionary Computation，2013，17(5)：686-704.

[15]CHEN X，KONG Y，FANG X，et al.A fast two-stage ACO algorithm for robotic path planning [J].Neural Computing and Applications，2013，22(2)：313-319.

[16]金飞虎，高会军，钟啸剑.自适应蚁群算法在空间机器人路径规划中的应用 [J].哈尔滨工业大学学报，2010，42(7)：1014-1018.

JIN Fei-hu，GAO Hui-jun，ZHONG Xiao-jian.Research on path planning of robot using adaptive ant colony system [J].Journal of Harbin Institute of Technology，2010，42(7)：1014-1018.

[17]WANG X，YANG G.Robot trajectory planning based on improved ant colony algorithm [J].Computer System & Applications，2010，19(11)：79-82.

[18]胡小兵，黄席樾.基于蚁群算法的三维空间机器人路径规划 [J].重庆大学学报，2004，27(8)：132-135.

HU Xiao-bing，HUANG Xi-yue.Path planning in 3-D space for robot based on ant colony algorithm [J].Journal of Chongqing University，2004，27(8)：132-135.

[19]刘利强，于飞，戴运桃.基于蚁群算法的水下潜器三维空间路径规划 [J].系统仿真学报，2008，20(14)：3712-3716.

LIU Li-qiang，YU Fei，DAI Yun-tao.Path planning of underwater vehicle in 3D space based on ant colony algorithm [J].Journal of System Simulation，2008，20(14)：3712-3716.

[20]朱庆保.蚁群优化算法的收敛性分析 [J].控制与决策，2006，21(7)：763-766.

ZHU Qing-bao.Analysis of convergence of ant colony optimization algorithms [J].Control and Decision，2006，21(7)：763-766.

[21]段海滨.蚁群算法原理及其应用 [M].北京：科学出版社，2005.

s： Supported by the Science and Technology Planning Project of Guangdong Province(2013B090600025,2015B010133002)

An Improved Three-Dimensional Path Planning Method of Mobile Robot

WUYu-xiangWANGChao

(School of Automation Science and Engineering， South China University of Technology， Guangzhou 510640， Guangdong， China)

In a known working environment, the three-dimensional global path planning of mobile robots is investigated in this paper. Firstly, both the updating strategy of global pheromone and the calculation method of pheromone increment in the ant colony algorithm are improved to make the planned path more reasonable. Next, the safety factor is introduced into the path planning and is calculated off-line in advance. Then, a fallback mechanism is designed to clear the pheromone of the point where ants fall into a deadlock, so as to achieve efficient obstacle avoidance of mobile robots in complex three-dimensional environment. Finally, the traditional search mode is improved to make the mobile robot move in the direction which is perpendicular to the main direction. Simulation results show that the above-mentioned path planning method is of a high searching efficiency with a shorter three-dimensional path, and it is more practical.

path planning； three-dimensional space； mobile robot； ant colony algorithm

1000-565X(2016)09-0053-08

2015-11-03

广东省科技计划项目(2013B090600025,2015B010133002);广州市科技计划项目(201508010016)

吴玉香(1968-),女,博士,教授,主要从事机器人控制研究.E-mail:xyuwu@scut.edu.cn

TP 242

10.3969/j.issn.1000-565X.2016.09.008