一种基于图的彩色图像分割算法*

沃焱　金璇

(华南理工大学 计算机科学与工程学院， 广东 广州 510006)



一种基于图的彩色图像分割算法*

沃焱金璇

(华南理工大学 计算机科学与工程学院， 广东 广州 510006)

为了解决图像分割中容易出现的过分割问题，提出了一种基于图的彩色图像分割算法.该算法在区域合并的基础上，首先用Mean shift方法进行预处理，得到初始过分割区域后对其构造邻接图，然后计算邻接区域的颜色、纹理及边缘特征相似性以判断区域是否需要合并直到所有满足条件的区域都被合并.为了保持图像的全局属性，文中通过查找最优合并成本的方式进行区域合并.实验结果表明：即使在图像目标和背景区域颜色比较相似时，文中算法也能较好地实现对目标区域的完整分割；与其他4种算法相比，文中算法具有更好的分割性能.

图像分割；Gabor滤波器；纹理；边缘；区域相似性

图像分割的目的是将整个图像分成若干个互不相交的非空子区域，每个子区域的内部是连通的，同一区域在亮度、颜色等特征上具有相似性，而相邻区域之间不具有相似性.分割问题是图像处理、计算机视觉中一个基础性和挑战性的问题，在图像识别、目标检测等技术中有重要的作用.该问题在20世纪70年代就受到了广泛的关注，人们提出了多种图像分割方法，如阈值方法[1]、聚类方法[2-3]、图论方法[4-5]、基于区域的方法[6-7]等.而基于图的分割方法[8-12]因能考虑到所有像素点携带的特征和空间信息而备受关注.在构造的图中，图顶点表示图像的像素点或区域，顶点之间用边连接，边的权值可以表示像素点或区域之间的不相似性.最早提出基于图的分割方法是Zahn[8]的基于最小生成树方法.该方法的分割标准是消除最小生成树中权值较大的边，权值为像素点之间的亮度差异，由于突变区域亮度大于稳定区域亮度，采用固定阈值和局部测量方式进行分割可能使突变区域被分成多个区域，或亮度较低区域被合并.为解决这个问题，Urquhart[9]提出了用最小权值对边进行归一化的分割方法，此方法容易导致错误分割，并且难以保持图像的全局属性.Felzenswalb等[10]提出了通过计算区域内部和区域之间的颜色差异来预测边界是否存在，从而进行区域合并.在这些以像素点为顶点的的图方法中，图像越大，顶点越多，且每个顶点需与周围的多个顶点建立邻接关系，使得图像处理复杂度较高.为解决这个问题，Rezvanifar等[11]先用Mean shift方法进行预处理，然后结合Ncut和AverageCut进行图像分割.Bo等[12]先用分水岭分割，再结合连续概率比测试和最大可能性标准进行合并预测，并动态合并满足条件的区域.这些方法中，图的顶点表示一个小的区域，每个顶点只需与周围少部分顶点建立连接，提高了图像处理速度.但这些方法仅根据颜色进行分割，当图像目标和背景区域颜色相似时，难以得到好的分割结果.

针对这些问题，文中结合图像的颜色、纹理和边缘特征，提出了一种基于图的彩色图像分割算法.为提高图像的分割速度，文中先使用Mean shift[13]进行预处理得到初始过分割区域，并利用这些区域构造相应的邻接图.为保持图像的分割完整性，文中提取了图像的边缘轮廓，并计算邻接区域的边缘相似性.为减少图像目标和背景颜色相似时的过分割现象，文中利用Gabor滤波提取图像的纹理特征，并通过统计邻接区域的纹理分布来计算其纹理相似性.为了保持图像的全局属性，文中根据查找最优合并成本的方式进行区域合并.

1　区域相似性度量

文中利用区域合并来分割图像.由于区域比像素点携带更多的信息，并且基于区域的处理方法能提高图像分割效率，因此文中先用Mean shift预处理得到初始过分割区域集合R={R1，R2，…，RN}，然后通过度量区域相似性将相似的区域进行合并.文中从颜色、纹理和边缘3个特征来度量区域相似性.

1.1颜色相似性

为度量区域颜色相似性，先将图像分成R、G、B三个通道，邻接区域Ri与Rj(Ri，Rj⊆R)的颜色差异Diff(Ri，Rj)可表示为

(1)

式中，pi′∈Ri，pj′∈Rj，cζ(pi′)、cζ(pj′)分别为像素点pi′、pj′在第ζ通道的颜色值，NRi、NRj分别为区域Ri、Rj的像素点个数.Diff(Ri，Rj)越大，Ri、Rj颜色相似的概率越小；反之，其颜色相似的概率越大.则邻接区域Ri、Rj颜色相似性条件可表示为

(2)

ε1为阈值.通过比较ε1与区域颜色差异大小来判断颜色相似性，因此ε1的取值应与图像颜色差异及分布相关.当区域颜色差异较大时，图像颜色分布比较分散，为避免过分割现象,ε1需相应地增大；当区域差异较小时，为避免欠分割现象，ε1需相应地减小.由于颜色的标准差能反映颜色的分布情况，因此文中利用图像颜色的标准差来计算ε1：

ε1=2[(stdR+stdG+stdB)/3]×max(Diff)

(3)

式中，max(Diff)为邻接区域对的最大颜色差异，stdR、stdG、stdB分别为图像在R、G、B通道归一化后的标准差.stdR、stdG、stdB越小，说明图像颜色分布越集中，颜色差异越小，对应的ε1值也越小；反之，stdR、stdG、stdB越大时，说明颜色分布越分散，对应的颜色差异越大，ε1值也越大.

1.2边缘相似性

为了较好地保证分割图像的完整性，合并前需考虑区域间是否有较强的边缘轮廓.Arbelaez等[14]利用局部多尺度信息和全局边缘信息提出了一种有效的提取边缘轮廓的方法.局部多尺度边缘信息和全局边缘信息的结合，既能提取出图像的边缘轮廓，又能凸显出显著的边缘，有效地对图像进行描述.基于这些优点，文中使用该方法来提取图像的边缘轮廓.

1.2.1边缘轮廓提取

对于局部边缘提取，该方法通过计算在LAB颜色空间中的L、a、b通道以及纹理通道的方向梯度信号G(x，y，θ)来预测像素点在θ方向存在边缘的概率.对于L、a、b通道的方向梯度，该方法先在像素点p′(x，y)处放置一圆盘，并在θ方向将圆盘划分成两半，然后求出两个半圆盘的亮度或者颜色直方图分布.两个半圆盘直方图h、h′的χ2距离就是像素点p′的方向梯度：

(4)

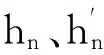
(5)

式中：mPb(x，y，θ)为像素点在(x，y)处θ方向的局部多尺度边缘概率；s为尺度；Gch，σ(ch，s)(x， y， θ)是颜色通道ch上以(x、y)为圆心、σ(ch，s)为圆盘半径，从角度θ上进行切分的两个半圆盘直方图的差异；αch，s为权值，用来衡量不同通道尺度下的概率分布.像素点的局部多尺度边缘能量可表示为

(6)

对于全局边缘检测，可用谱聚类将局部多尺度信息结合到全局框架.首先根据局部多尺度边缘概率定义相似矩阵Wij，

(7)

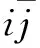
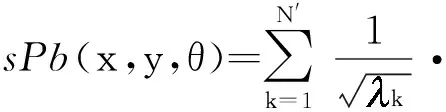
(8)

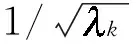
μ×sPb(x，y，θ)

(9)

式中，βch，s和μ为权值.对于像素点的全局边缘能量，可以用像素点的最大gPb边缘概率来表示：

(10)

1.2.2边缘相似性判断

由于gPb用边缘梯度信号描述，梯度越大，存在边缘的可能性越大.而邻接区域的边缘相似性主要在于检测邻接区域边界之间是否存在边缘，因此文中根据邻接区域间相邻边界点的梯度概率来度量边缘相似性.

在图1所示的示例中，Ri、Rj为邻接区域.Ri、Rj的相邻边界点集合P={pm|1≤m≤NP}，NP为Ri、Rj之间的相邻边界点个数.根据边界点的梯度幅值可将Ri、Rj间的边缘梯度概率Grad(Ri，Rj)表示为

图1邻接区域分布图

Fig.1Distributionofadjacentregions

边界点集合P的边缘概率平均值：

式中，pm(x)、pm(y)表示第m个边界点的x、y坐标.Grad(Ri，Rj)越大，Ri、Rj之间存在边缘的可能性越大，两区域边缘特征越不相似；反之，Grad(Ri，Rj)越小，Ri、Rj之间存在边缘的可能性越小，边缘相似的概率越大.因此，Ri、Rj的边缘相似性条件可表示为

(12)

式中，ε2为阈值.当区域边界点的梯度概率小于ε2时，邻接区域具有边缘相似性；反之，则不具有边缘相似性.

1.3纹理相似性

纹理是图像处理中的常用特征.在文献[10-12]方法中，仅用颜色特征来进行图像分割，当背景和目标区域颜色相似时，难以得到较好的分割结果，因此在合并时需要考虑区域间的纹理相似性.

Gabor滤波[15]是一种常用的提取纹理的方法，能有效提取不同方向和尺度的纹理信息.因此，文中用Gabor滤波器来提取纹理特征.二维Gabor滤波器表示为

(13)

式中,x′=xcosθ′+ysinθ′，y′=-xsinθ′+ycosθ′，ϑ为波长，θ′为Gabor核函数方向，ψ为相位偏移，δ为高斯标准差，γ为空间纵横比.

(14)

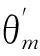
(15)

(16)

当Ri中所有像素点投完票，可获得图2(a)所示的纹理分布.直方图在θ′方向上的能量分布可表示为

(17)

式中，E′(x(k),y(k),θ′)为Ri中第k个像素点在θ′方向上的权值.同理，对区域Rj纹理统计后，可得到图2(b)所示的纹理分布.

(a)Ri纹理分布(b)Rj纹理分布

图2图1中Ri、Rj的区域纹理分布

Fig.2Texture distribution of regionsRiandRjin Fig.1

统计邻接区域Ri、Rj的纹理分布后，其纹理差异可以表示为

(18)

tDist(Ri，Rj)越大，Ri与Rj纹理相似的概率越小，反之纹理相似的概率越大.因此，区域Ri、Rj的纹理相似条件可表示为

(19)

ε3为参数.当两区域之间的纹理差异小于ε3时，两个区域在纹理上有相似性，反之不具有相似性.

1.4区域合并条件

合并条件是区域合并的关键.文中度量了图像颜色、纹理以及边缘特征的相似性，如果仅把颜色相似性作为合并条件，当目标和背景区域颜色相似时，容易将目标和背景区域融合.同理，如果仅把纹理或者边缘相似性作为最终合并条件，也难以获得较好的分割结果.若利用颜色和纹理或者颜色和边缘相似性作为合并条件，与之前单一特征相比，合并效果应该要好，但如果将颜色、纹理和边缘特征相结合，使得合并条件更加严格，既能使相似的区域被合并，又能够有效地减少过分割现象.因此，文中结合颜色、纹理以及边缘特征相似性，将构造的区域合并条件表示为

C′(Ri，Rj)=C1(Ri，Rj)C2(Ri，Rj)C3(Ri，Rj) (20)

仅当C′(Ri，Rj)=1时才进行合并，此时C1(Ri，Rj)、C2(Ri，Rj)、C3(Ri，Rj)均为1，表明区域Ri、Rj在颜色、纹理和边缘特征上都具有相似性.

2　基于图的区域合并

2.1邻接图的构造

为了更好地描述图像，文中对Mean shift[13]产生的过分割区域集合R构建邻接图.令G′=(V，e)表示一个无向图，V是图的顶点集合，对图进行初始化时V=R.(vi，vj)∈e，e是边集合，(vi，vj)表示连接顶点vi和vj的边，该边的上的权值w((vi，vj))用于衡量vi、vj的不相似性.结合区域在颜色、纹理和边缘特征上的差异，可将连接vi、vj的边的权值w((vi，vj))表示为

w((vi，vj))=Diff(vi，vj)+Grad(vi，vj)+

tDist(vi，vj)

(21)

2.2区域合并过程

在区域合并过程中，合并顺序的优劣能反映算法能否保持图像全局属性.由于区域之间的差异性，合并时会产生合并成本，记为costF，差异越大，costF越大.为使合并顺序最优，每次合并时costF应最小.由于边的权值能反映区域间的差异，因此区域Ri和Rj之间的costF可用权值表示,即

costF(Ri，Rj)=w((Ri，Rj))

(22)

在合并过程中，选择costF最小的边(Ri，Rj)，若Ri、Rj满足合并条件就将Ri、Rj合并，并更新与Ri、Rj相关联的边.若Ri、Rj不满足合并条件，因其他边的costF比costF(Ri，Rj)大，表明其他区域间的颜色、纹理以及边缘上的特征差异更大，因而不会满足合并条件，此时区域合并可以终止.

合并算法的步骤如下：

1)利用式(22)计算出邻接图中所有边的合并成本costF.

2)在边集合e中选择合并成本costF最小的边(Ri，Rj)，利用式(20)计算C′(Ri，Rj).

3)若C′(Ri，Rj)=1，则将Ri合并入Rj，并对邻接图作以下更新.

(a)删除Ri与Rj间的边(Ri，Rj)；

(b)对于所有从Ri出发的边(Ri，Rkk)，删除边(Ri，Rkk)，若在集合e中不存在边(Rj，Rkk)，则建立边(Rj，Rkk)；

(c)对于所有从Rj出发的边(Rj，Rll)，利用式(22)重新计算costF(Rj，Rll)；

(d)返回步骤2).

4)若C′(Ri，Rj)=0，则终止区域合并，输出分割结果.

2.3区域合并属性

文中利用查找最优合并成本的方式进行合并，可以保持图像的一些全局属性，既不产生过分割也不产生欠分割.

为证明文中算法满足这一属性，文中参照文献[10]方法中精细和粗糙分割的概念定义过分割和欠分割.若分割S中包含一些满足合并条件但没合并的区域对，则称S过分割；若S存在另一个分割S′，S′中邻接区域之间有明显的边界，且S′的每个区域都包含在S的一些块中，S′能通过S的一次或多次划分得到，则称S是欠分割的.另外，若两区域的边缘特征不相似，则区域之间存在边界.

如果S是欠分割，则S中存在另一个分割S′，S′的邻接区域之间存在边界.令区域C∈S，邻接区域A，B∈S′，A⊂C，B⊂C，且A和B之间有最小costF.由文中算法可知，在A和B合并之前不会和C中其他区域合并，与C包含A、B矛盾.因此S不是欠分割.

综上所述，文中算法在区域合并过程中能保持图像的全局属性，既不产生过分割也不产生欠分割.

3　实验分析

3.1分割评估数据库

为验证文中算法的分割性能，文中采用分割评估数据库(SED)[16]进行实验.该数据库包含100幅彩色图像及对应的标准分割结果，每幅图像含有单一目标区域，且背景和目标亮度、纹理等特征都有所不同.

为评估分割质量，文中采用式(23)计算F值[17]来评估分割结果与标准分割结果的一致性.

(23)

式中：r1为查全率；r2为查准率；F为两个指标的综合，反映了算法的分割性能，F越大，分割质量越好.

3.2实验参数设置

实验参数设置如下：Gabor滤波器相位偏移ψ为0，空间纵横比γ为1，波长ϑ和标准差δ分别为4和3.度量边缘、纹理相似性的阈值ε2和ε3需适当调整.ε2较小可使少数区域被合并而形成欠分割，ε2较大可能导致过分割.为得到较好的分割效果，文中ε2取为53.对于ε3，先用标准差求得图像在8个方向上的纹理分布，标准差越大，纹理差异越大.实验中当标准差大于0.32时，图像的纹理差异明显，为使纹理相似区域能合并，ε3取0.3；反之，当标准差小于0.32时，图像平滑纹理差异不明显，若ε3取值与前者一致，则可能使目标和背景融合导致过分割，此时ε3取0.2.

3.3分割结果

3.3.1图像分割结果

对图3(a)所示原图进行图像分割，原图边缘轮廓如图3(b)所示.图3(c)为Mean shift[13]预处理的结果.为完整地分割出目标区域，文中利用过分割区域构造邻接图，并迭代合并具有相似性的区域，迭代70和150次的结果分别如图3(d)和3(e)所示，与图3(c)相比，区域个数明显减少，目标区域边缘逐渐清晰，仍有需合并的区域；迭代合并300和325次的结果如图3(f)和3(g)所示，图中背景相似区域被合并，目标区域基本分割完成；最终的分割结果如图3(h)所示，其目标边缘轮廓与图3(b)中显著边缘轮廓一致，说明文中算法能较好地实现对目标区域的完整分割.

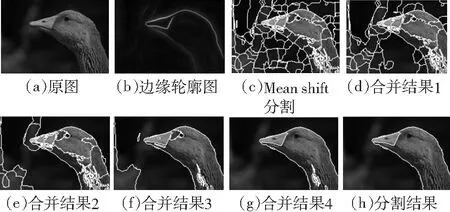
图3图像分割结果

Fig.3Results of image segmentation

3.3.2纹理、边缘对分割效果的影响

为验证纹理、边缘对分割效果的影响，采用文中算法从颜色、颜色+纹理、颜色+边缘、颜色+纹理+边缘4种情况对图4(a)、5(a)进行分割实验，结果如图4和5所示.

图4强纹理、弱边缘分割结果

Fig.4Segmentation results of strong texture and weak contour

图5弱纹理、强边缘分割结果

Fig.5Segmentation results of weak texture and strong contour

由于图4(a)的目标和背景颜色相似，若仅用颜色，则目标与背景融合，分割结果如图4(c)所示；因原图部分边缘模糊(见图4(b))，故未能分割出完整的边缘(见图4(e))；引入纹理后，能较好地分割出目标区域(见图4(d))；颜色、纹理和边缘的结合能获得完整的边缘，还能消除一些细小的区域(见图4(f)).图5(a)的目标和背景区域颜色相似且纹理差异较小，仅用颜色同样使目标区域与背景融合(见图5(c))，纹理的引入也不能获得完整的边缘轮廓(见图5(d)).因图5(b)的边缘轮廓完整，故加入边缘后图5(e)、5(f)能完整地提取目标区域.

颜色、颜色+纹理、颜色+边缘、颜色+纹理+边缘的分割评估结果分别为0.611、0.665、0.693、0.784.可知，引入纹理和边缘能提高文中算法的分割性能，颜色、纹理和边缘的结合，可使目标区域轮廓完整，分割效果更优.

3.3.3分割结果评估与比较

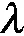
(a)目标与背景有相似颜色及纹理情况下的分割结果

(b)目标与背景的颜色及纹理差异较大情况下的分割结果

(c)目标与背景的颜色相似、纹理不同情况下的分割结果

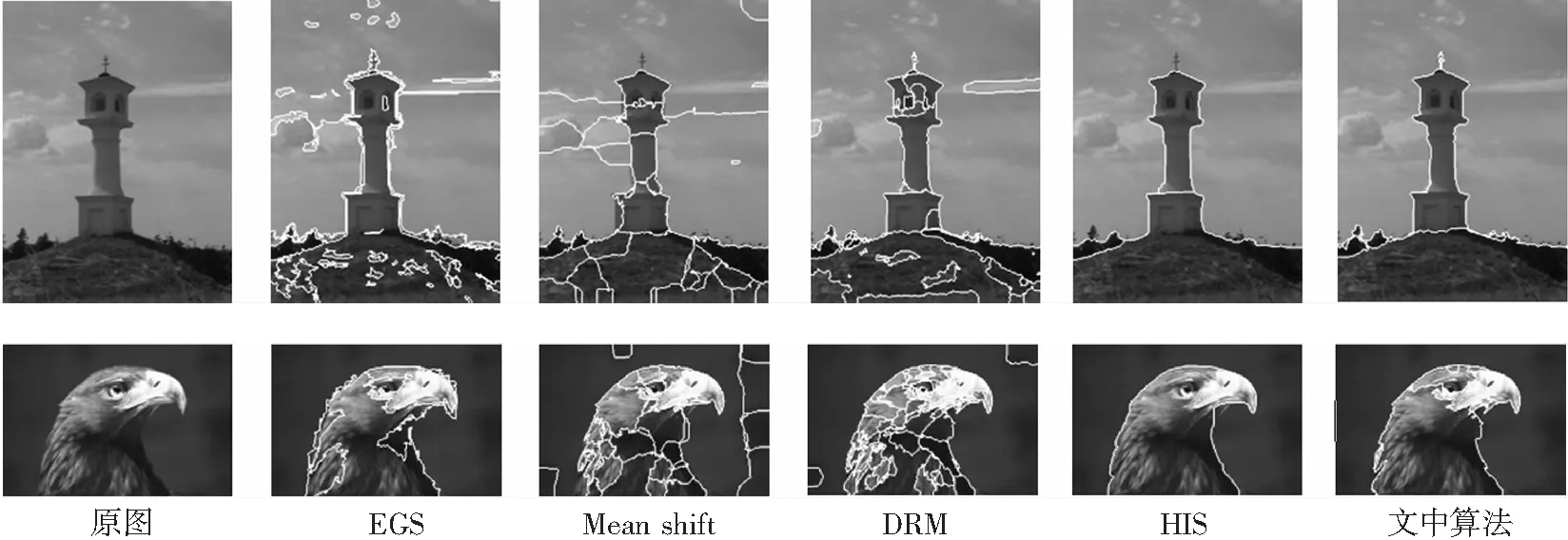
为评估算法的分割性能，文中利用式(23)计算F值对以上5种算法进行评估，文中算法、HIS[14]、EGS[10]、DRM[12]、Mean shift[13]的F值分别为0.784、0.781、0.602、0.460、0.440.由此可知，同其他的分割算法相比，文中算法有更好的分割性能.

4　结论

文中提出了一种基于图的彩色图像分割算法.该算法采用区域合并的方式，先用Mean shift预处理得到初始过分割区域，并利用这些区域构造邻接图；然后通过度量图像在颜色、纹理和边缘特征的相似性来构造区域合并条件.为了获得较优的合并顺序，文中采用查找最优合并成本的方式进行区域合并，以保持图像的全局属性.在SED数据库上的实验结果表明，与现有算法相比，文中算法具有更好的分割性能，在目标和背景区域颜色较相似的情况下，能较好地实现对目标区域的完整分割.

[1]杨震伦，闵华清，罗荣华.基于改进量子粒子群优化的多阈值图像分割方法 [J].华南理工大学学报(自然科学版)，2015，43(5)：126-138.

YANG Zhen-lun，MIN Hua-qing，LUO Rong-hua.Multi-threshold image segmentation algorithm based on improved quantum-behaved particle swarm optimization [J].Journal of South China University of Technology(Natural Science Edition)，2015，43(5)：126-138.

[2]GONG Mao-guo，LIANG Yan，SHI Jiao，et al.Fuzzyc-means clustering with local information and kernel metric for image segmentation [J].IEEE Transactions on Image Processing，2013，22(2)：573-584.

[3]周晓明，李钊，刘雄英.一种基于改进FCM的自动图像分割 [J].华南理工大学学报(自然科学版)，2014，42(3)：1-7.

ZHOU Xiao-ming，LI Zhao，LIU Xiong-ying.An automatic image segmentation algorithm based on improved FCM [J].Journal of South China University of Technology(Natural Science Edition)，2014，42(3)：1-7.

[4]BO Peng，ZHANG L，ZHANG D.A survey of graph theoretical approaches to image segmentation [J].Pattern Recognition，2013，46(3)：1020-1038.

[5]SHI J，MALIK J.Normalized cuts and image segmentation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(8)：888-905.

[6]LI Tai-yong，XIE Zhi-long，WU Jiang，et al.Interactive object extraction by merging regions withk-global maximal similarity [J].Neurocomputing，2013，120(23)：610-623.

[7]TAN Xiao，SUN Chang-ming，SIRAULT X，et al.Stereo matching using cost volume watershed and region merging [J].Signal Processing：Image Communication，2014，29(10)：1232-1244.

[8]ZAHN C T.Graph-theoretic methods for detecting and describing gestalt clusters [J].IEEE Transactions on Computers，1971，20(1)：68-86.

[9]URQUHART R.Graph theoretical clustering based on limited neighborhood sets [J].Pattern Recognition，1982，15(2)：173-187.

[10]FELZENSWALB P，HUTTENLOCHER D.Efficient graph-based image segmentation [J].International Journal of Computer Vision，2004，59(2)：167-181.

[11]REZVANIFAR A，KHOSRAVIFARD M.Including the size of regions in image segmentation by region-based graph [J].IEEE Transactions on Image Processing，2014，23(2)：635-644.

[12]BO Peng，ZHANG L，ZHANG D.Automatic image segmentation by dynamic region merging [J].IEEE Tran-sactions on Image Processing，2011，20(12)：3592-3605.

[13]COMANICIU D，MEER P.Mean shift：a robust approach toward feature space analysis [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(5)：603-619.

[14]ARBELAEZ P，MICHAEL M，FOWLKES C，et al.Contour detection and hierarchical image segmentation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(5)：898-916.

[15]FORGEL I，SAGI D.Gabor filters as texture discriminator [J].Biological Cybernetics，1989，61(2)：103-113.

[16]ALPERT S，GALUN M，BASRI R.Image segmentation by probabilistic bottom-up aggregation and cue integration [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(2)：315-327.

[17]HRIPCSAK G，ROTHSCHILD A S.Agreement，the F-measure，and reliability in information retrieval [J].Journal of the American Medical Informatics Association，2005，12(3)：296-298.

s： Supported by the National Natural Science Foundation of China(61472145),the Natural Science Foundation of Guangdong Province(2016A030313472) and the Special funds for University-Industry Cooperation of Guangdong Province and the Ministry of Education of China(2013B090500015)

A Graph-Based Color Image Segmentation Algorithm

WOYanJINXuan

(School of Computer Science and Engineering， South China University of Technology， Guangzhou 510006， Guangdong， China)

In order to solve the over-segmentation problem in the image segmentation, a graph-based color image segmentation algorithm is proposed. In the algorithm, on the basis of the region-merging method, the over-segmentation regions are obtained by using Mean shift to preprocess an image, and for the over-segmentation regions, a region adjacency graph is constructed. Then, the color, texture and edge contour similarities between adjacency regions are measured to judge if adjacency regions need to be merged, until all the satisfactory regions are merged. Besides, the regions are merged by searching the optimal merging-cost, so as to preserve some global prosperity of the image. Experimental results indicate that the proposed algorithm can completely segment object regions even when the color features between background regions and object regions of an image are similar, and it has a better segmentation performance in comparison with four state-of-the-art segmentation algorithms.

image segmentation； Gabor filters； textures； edge； regional similarity

1000-565X(2016)09-0001-08

2015-11-15 20

国家自然科学基金资助项目(61472145);广东省自然科学基金资助项目(2016A030313472);华南理工大学中央高校基本科研业务费专项资金资助项目(2015ZZ031);广东省-教育部产学研合作专项(2013B090500015)

沃焱(1975-),女,博士,教授,主要从事多媒体应用技术研究.E-mail:woyan@scut.edu.cn

TP 391.41

10.3969/j.issn.1000-565X.2016.09.001