矩阵型多类代价敏感分类器模型

孟 芸， 王 喆（华东理工大学计算机科学与工程系，上海 200237）

矩阵型多类代价敏感分类器模型

孟 芸， 王 喆
（华东理工大学计算机科学与工程系，上海 200237）

目前大部分分类器都是以分类正确率来衡量性能，这种评价标准都是基于理想情况下所有错误分类代价都是相同的。但实际生活中往往不同的错误分类会带来不同的损失，因此代价敏感学习成为模式识别中一个热点研究领域。本文将代价敏感思想与矩阵型学习机相结合，提出了一个矩阵型多类代价敏感分类器模型。通过与其他分类器在常用数据集上的对比实验证明，该方法降低了错误分类代价，提高了少数类或代价高类别的分类正确率，并可以在有效次内收敛，是一个有效且实用的方法。

模式识别；代价敏感；分类器设计

分类器设计是机器学习和模式识别领域重要的一部分。目前大多数分类模型都侧重于使用分类正确率来衡量一个算法的性能，并默认这种评价标准都是基于所有错误分类代价是相同的。但是实际生活中的分类问题，数据错误分类代价往往不相等［1-2］。比如，在门禁系统的家庭成员识别问题上，将一个家庭成员识别错误使其不能进入引起的代价远远小于将一个不属于家庭成员的陌生人误识别使其进入房屋带来的损失。对于这类错误分类代价不同的情况，如在信用卡欺诈检测、医疗、网络入侵检测等领域，仅使用传统的代价不敏感分类器并不能达到很好的分类效果［3］。而代价敏感学习的目标就是通过最小化错误分类总代价做出最优决策，因此，将代价敏感思想引入到分类器设计中具有十分深远的意义［4］。

本文提出了一种新型的代价敏感学习模型——矩阵型多类代价敏感分类器（Cs Mc Mat MHKS），实验表明，该方法与矩阵型多类代价不敏感的Mc Mat MHKS分类器相比，有效地降低了错误分类总代价并提高了少数类的分类正确率。

1　代价敏感学习

1.1代价敏感研究现状

代价敏感学习方法是机器学习中的一种新方法，不同于传统分类方法尽可能降低错误分类率，它主要是将各类不同的误分代价引进到分类决策中以降低错误分类的总体代价［3-5］。目前，代价敏感学习算法的研究主要集中在以下几个方面：

（1）基于重采样的方法，也叫重构训练集的方法。根据代价矩阵改变原始样本分布重构训练集，再结合一种基于最小错误率的分类方法进行训练并分类［6］。通过不同的采样方法，如过采样、欠采样或者两者结合的形式［7］将分布不平衡的训练数据调整为均匀分布的数据。过采样是通过随机复制或者其他方式生成少数类样本，改变训练集样本中的分布，达到样本类别的均衡，也可以根据代价信息过采样样本。过采样的缺点是会增加额外的信息或噪声，不一定能达到一个较好的结果。欠采样既也是改变训练集众数据分布使各类样本达到平衡，与过采样不同的是，它通过降低低代价样本数目来达到目的，同时，这种方式会损失一部分可能携带重要信息的样本，对分类造成不必要的影响。而混合采样则是把两者结合起来以求更佳效果的方法，实验证明，混合采样继承了过采样与欠采样的优点，又尽量避免了它们的缺点，已被广泛采用。

（2）基于对分类结果的后处理，即按照传统学习方法学习一个分类模型，然后对分类结果按照贝叶斯风险理论进行调整，以达到损失最小。较为著名的MetaCost方法［8］是一个将普通分类器转化为代价敏感分类器的最普遍方法，它不依赖于所使用的具体分类器，对分类算法不作改变，经过多次取样，把训练集分为多个子模型训练多个分类器，综合各个分类器给出的分类结果估计样本的后验概率，再计算错误分类总代价［9-10］，根据最小代价修改类标号。MetaCost方法主要有两个方面的缺点：一是对训练集进行重新标记，再利用数据集来反映代价敏感性的有效性还需进一步验证［1］；二是不能准确地对后验概率进行估计。

（3）直接构造一个代价敏感的学习模型或者修改已有的分类算法，将代价的影响嵌入到决策的过程［10-11］。最常用的方法有可以直接处理样本权重的决策树、代价敏感人工神经网络和代价敏感支持向量机等［12-14］。如神经网络，有多种方法可以使神经网络转化为代价敏感算法，如得到测试样的后验概率，再使用贝叶斯风险决策，或者改变输出层每次迭代时的输出，使其代价敏感等。文献［15-16］用指数形式表示的极值问题替换用符号函数表示的错误分类代价极值问题，结合递推得到了可以直接应用于多分类问题的代价敏感学习的AdaBoost算法。

1.2矩阵型多类分类模型

面向矩阵的修正Ho-Kashyap分类器（Mat MHKS）［17］是一种可以直接处理矩阵模式的分类器，目前这个方法仅基于两类情况设计，在多分类问题上使用“一对一”策略实现，时间复杂度较大。矩阵型多类分类器Mc Mat MHKS是一种直接多类矩阵型分类器［18］，在实际的多类分类问题上，传统的二元分类器将多类分类问题分解成多个两类分类子问题，通过综合各个子分类器的分类结果得出最终决策，而Mc Mat MHKS则是直接得出最后的分类结果，相比于传统的两类分类方法，直接法与矩阵化思想的结合，在保持了数据分类精度的同时也降低了分类的时间复杂度。

2　矩阵型多类代价敏感分类器Cs Mc Mat MHKS

本文中代价矩阵的设置采用常用的基于类别的代价敏感，即每一类样本被错误分类所带来的代价相等，而不同类别之间不相等［19-20］。假设C（i，j）为代价矩阵，行表示类别，列表示预测类别，Cij表示第i类样本被错误分类为第j类样本的代价。为了方便计算，对每一样本采用以式（1）表示的这一类样本被错误分类的代价，这一类的每个样本被错误分类的代价相同［5，13，21］，即

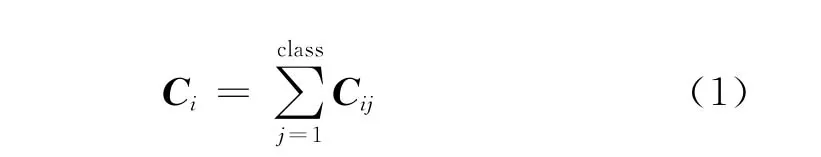
Mc Mat MHKS的判别函数如下：

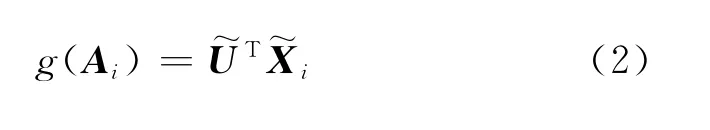
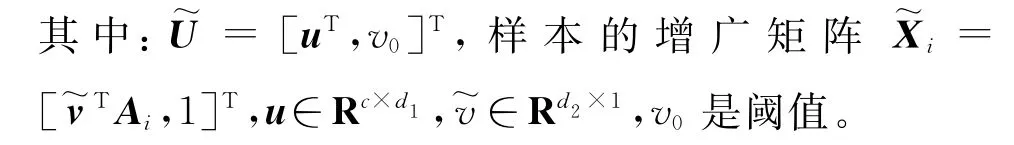
单纯地把样本代价嵌入判别函数使代价参与决策面偏移，经实验证明结果会根据代价的设置不同而比较随机。现设计加入样本权重系数，其与样本错误分类代价成反比，如式（3）所示。即当一类样本被分错的风险对总体分类结果影响较大时，可能会过拟合，我们试图减小各样本错误分类误差在总体中的比重来均衡各样本对分类结果的总体贡献，以期获得分类代价和推广能力能达到一种平衡［1，5-6］。

根据公式以及代价矩阵为每一样本设置权重系数，同一类别的样本权重系数相同［22］。对于判别函数式（2），可以通过转换为最小化总分类风险求得判别函数中权向量的最优解。

Cs Mc Mat MHKS的准则函数由经验风险和结构风险两部分组成。

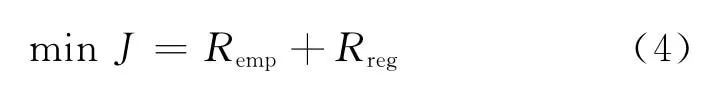
其中加入权重系数ω后的经验风险Remp计算如下：

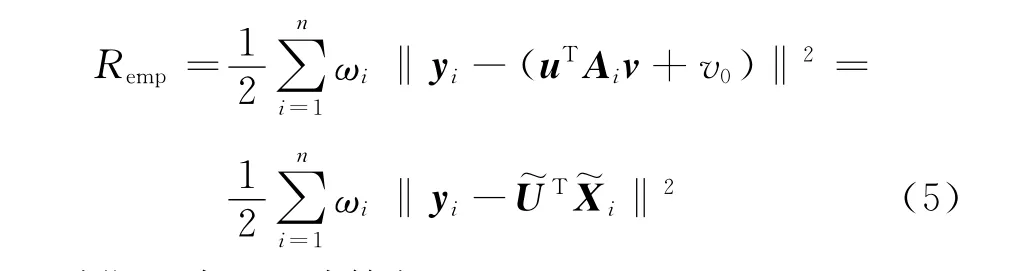
正则化风险Rreg计算如下：

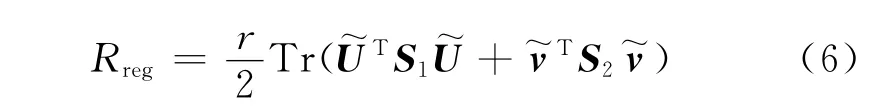
式中：r为正则化系数；S1和S2是两个单位矩阵，S1=（d1＋1）Id1×d1，S2=（d2＋1）Id2×d2。

可以看出，当所有样本错误分类代价相同时，由式（3）可知，Ci/Cj=1。同时各样本权重系数比例一致，ωi=ωj，即当系数都为1时，判别函数式（2）就是代价不敏感的Mc Mat MHKS，因此本文方法也是对Mc Mat MHKS的扩展。

将式（5）、式（6）代入到式（4）可以得到

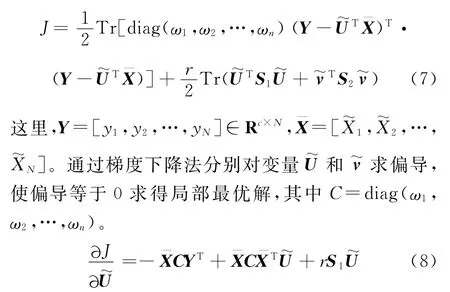
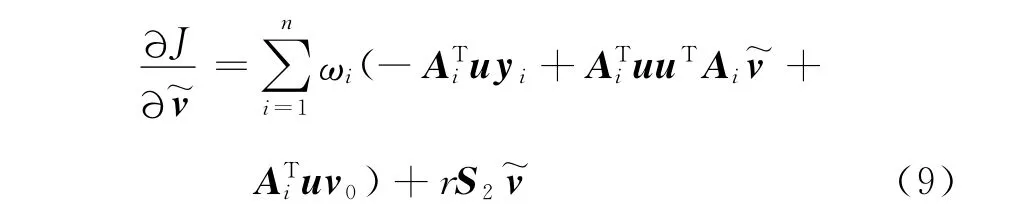
在分类器最终决策阶段，假设一个训练数据（Ai，yi），把它判为第j类，应当满足式（10）。

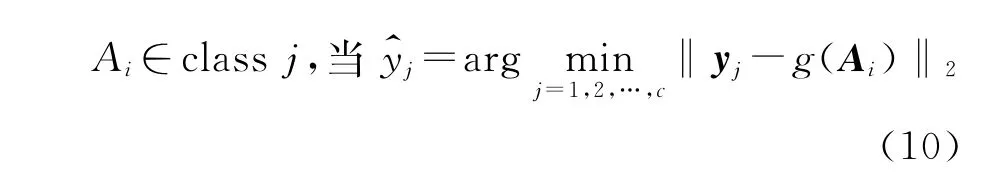
Cs Mc Mat MHKS算法步骤如下：

（1）根据样本每一类别样本数目，设置代价矩阵C；根据式（3）设置样本的权重系数ωi，同一类别样本的权重系数相同。

3　实 验

3.1实验设置

实验过程中，代价矩阵是自定义的，为了证明不同代价矩阵情况下算法的有效性，设置了两种不同的代价矩阵进行实验。本文采用的数据集来自UCI基准数据集［23］中常用的两个平衡数据集Banana和Water，以及不平衡数据集Breast Cancer Wisconsin （BCW）、Ionosphere和Ecoli。表1示出了各数据集的具体相关信息，表2示出了具体的代价设置。

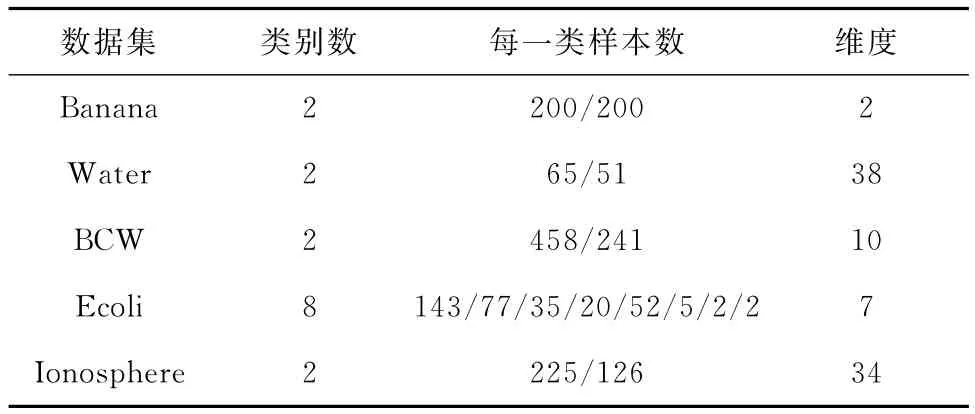
表1　数据集具体信息Table 1 Information of the datasets

实验中设定数据集中的一半数据用于训练，另一半用于测试。正则化系数来自集合｛10－3，10－2，10－1，1，10，102｝。对比算法来自同一分类器家族，分别是本文方法Cs Mc Mat MHKS、Cost-blind Mc Mat MHKS、面向矩阵的修正Ho-Kashyap分类器（Mat MHKS）和修正Ho-Kashyap分类器（MHKS）［17］。针对UCI数据形式，同时也将向量型样本转换成多个矩阵型数据并从中选择最优的表示形式。例如BCW样本维度为10，则转化为矩阵形式有1×10，2×5，5×2和10×1共4种，其他数据集进行同样处理。因数据集不同，每个对应的预设代价矩阵也不相同，遵循的基本规则是不平衡数据集中少数类样本被错误分类代价高于多数类样本代价，而平衡数据集中根据类别可随机自定义。实验过程中，采用10轮Monte Carlo交叉验证（MCCV）［24］，即每一个参数重复10次实验，最终求得平均值，以保证实验的准确度。MCCV与一般的交叉验证不同的是，每次循环它从整个数据集中无放回的选择数据构建训练集，剩余的做测试集，这样能够保证训练测试集都是有变化的并且每个划分不重复。MCCV能够避免训练规模过大，减少过拟合，因此，选用MCCV来验证本文方法的稳定性和可信性。对于不平衡数据集，单纯的分类正确率并不能很好地评估分类器性能，因此在不平衡数据集上采用了常用的G-means［25］作为评价标准。

表2　各数据集对应错误分类代价比例设置的代价矩阵（第1类/第2类/…/第n类）Table 2 Settings of cost matrix on the datasets（Costclass1/ Costclass2/…/Costclass n）

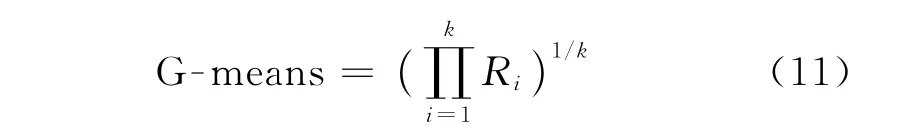
其中：Ri表示每一类的分类正确率；k表示类别总数。

3.2实验结果

表3和表4示出了代价敏感Cs Mc Mat MHKS （Cs）、代价不敏感Cost-blind Mc Mat MHKS（Cb）、Mat MHKS和MHKS在4个数据集Banana、Water、BCW和Ionosphere上的实验结果，评价指标包括分类总代价SumCost、G-means、分类正确率，并列出了达到最优结果时对应的矩阵表示形式和正则化系数r的值，其中分类总代价最低的算法数据用黑体表示，G-means最高的值以下划线标出。图1示出了Cs与Cb在Ecoli数据集上各类别的分类正确率对比结果。

本文在Banana和Ecoli数据集上对式（7）进行了收敛性分析，收敛曲线如图2所示。图2中横坐标表示迭代次数，纵坐标表示目标函数的对数值。

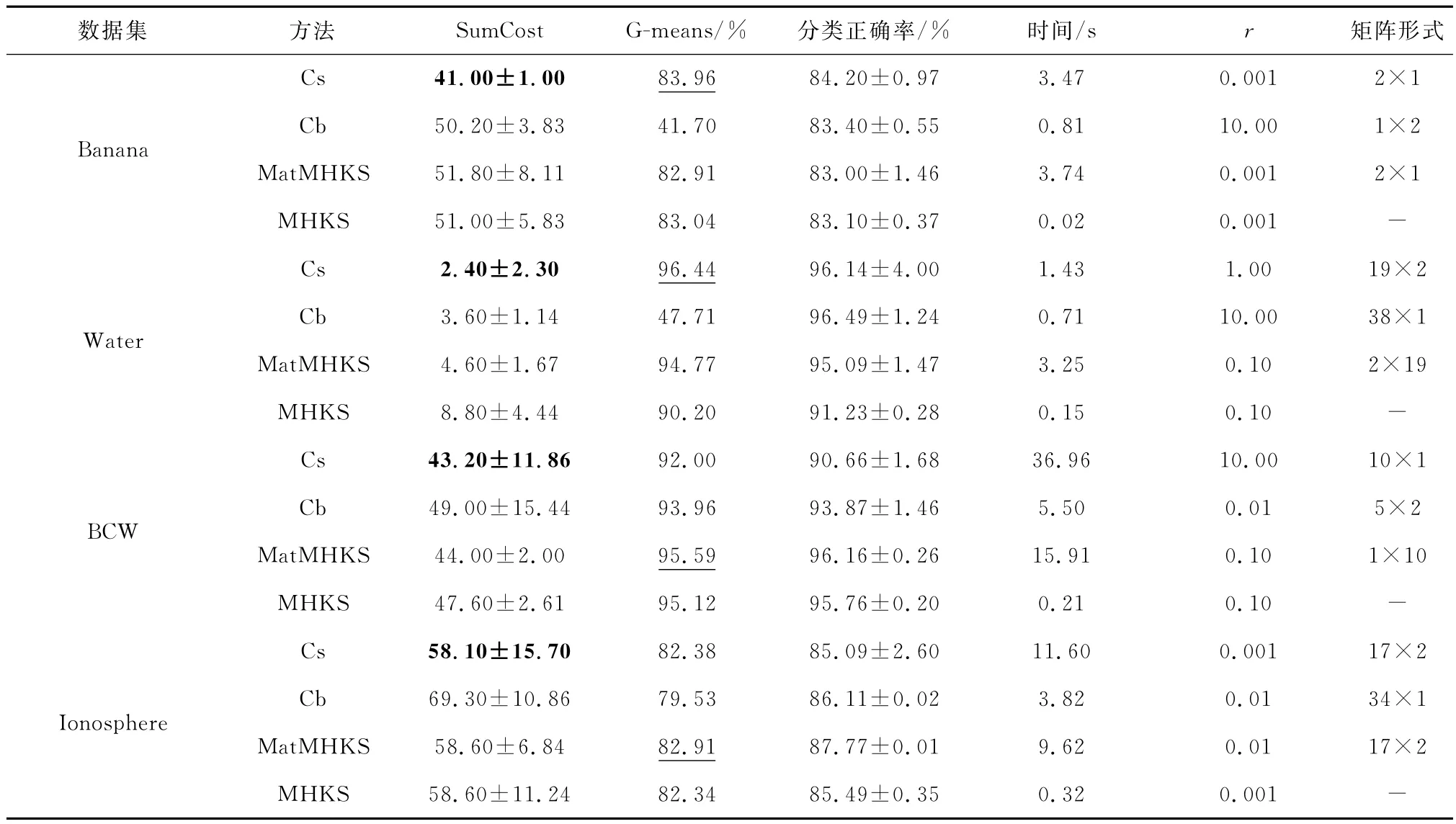
表3　第1种代价矩阵下Cs，Cb，Mat MHKS，MHKS在4个数据集上的实验结果Table 3 Experimental results of Cs，Cb，Mat MHKS and MHKS on Banana，Water，BCW and Ionosphere

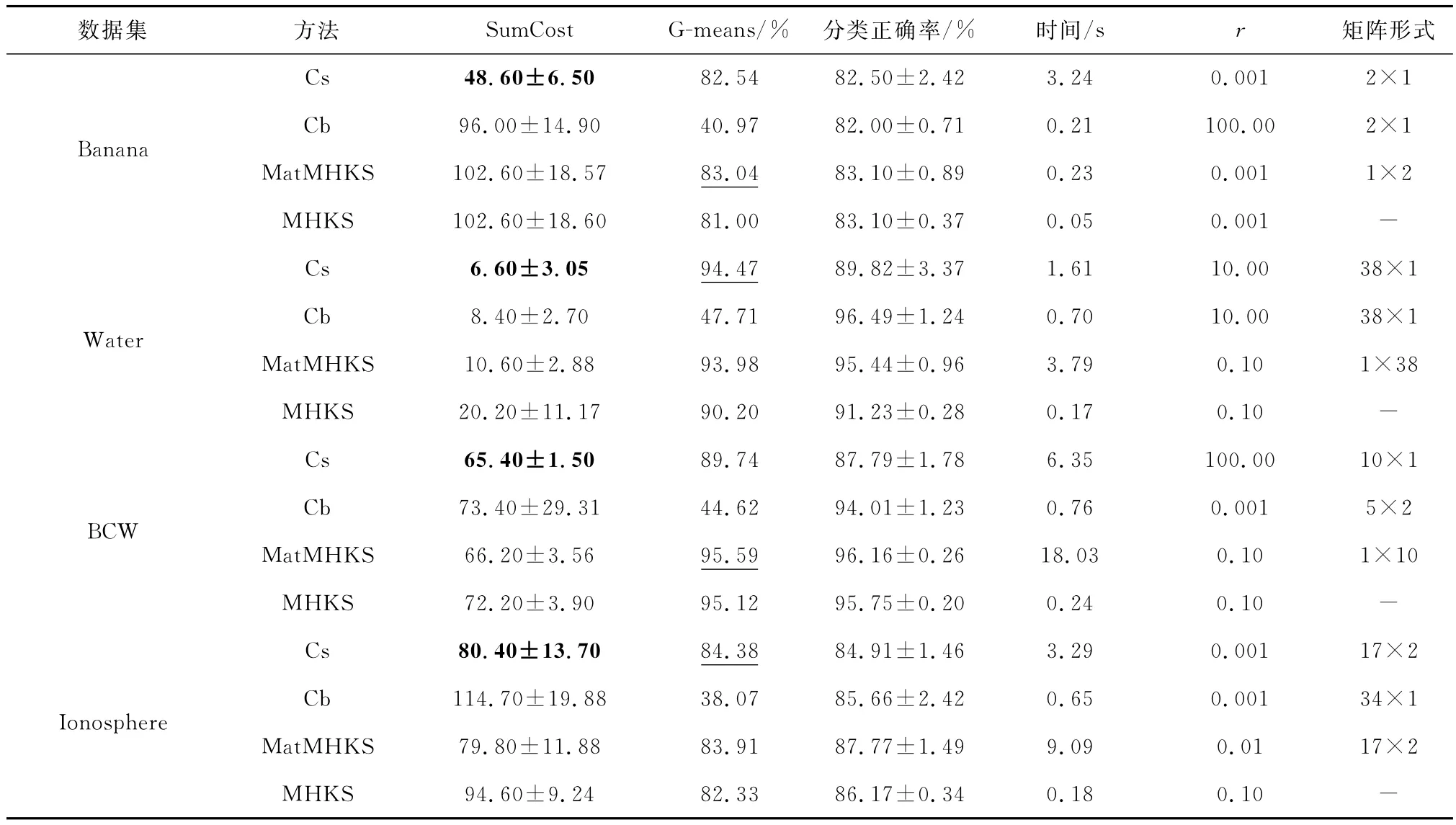
表4　第2种代价矩阵下Cs，Cb，Mat MHKS，MHKS在4个数据集上的实验结果Table 4 Experimental results of Cs，Cb，Mat MHKS and MHKS on Banana，Water，BCW and Ionosphere

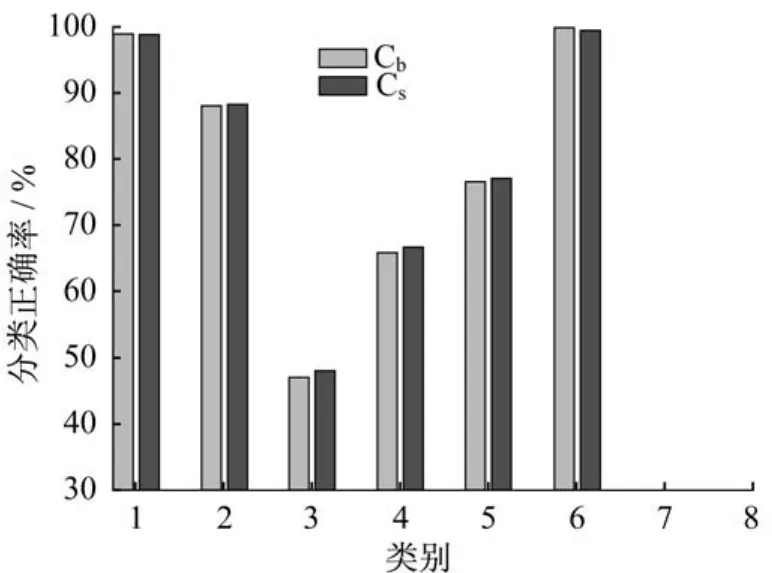
图1　Cs和Cb在Ecoli上每一类对应的分类正确率Fig.1 Accuracy of Cs Mc Mat MHKS and Cost-blind Mc Mat MHKS on Ecoli classes

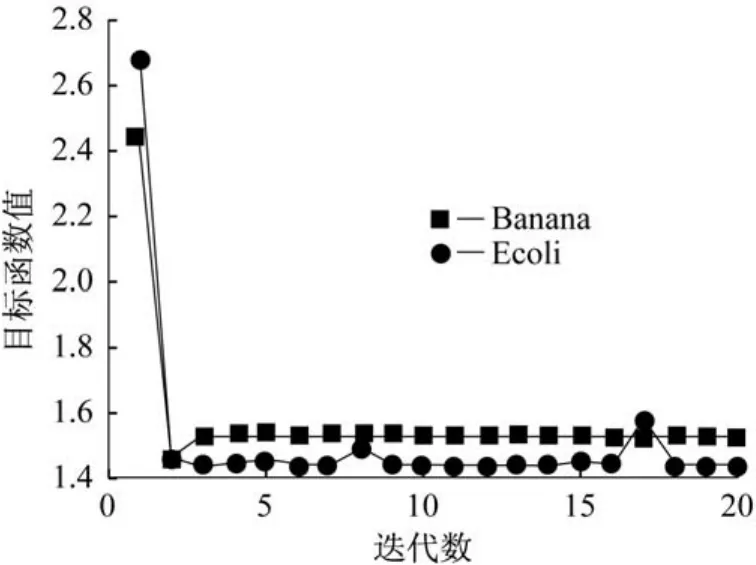
图2　Cs在Banana和Ecoli上的收敛曲线Fig.2 Convergence analysis of Cs Mc Mat MHKS on Banana and Ecoli

3.3实验结果分析

从表3和表4中可以看出：

（1）本文方法在大部分数据集上与代价不敏感的Mc Mat MHKS、Mat MHKS和MHKS相比达到了最小错误分类总代价，尤其是当样本类别之间的代价比例差别变大时，效果更为明显。例如，Banana数据集在第1种代价比为1/2时，本文方法与最大错误分类代价之差为10.80，而在第2种代价比为1/5时，本文方法与最大错误分类代价之差为54。实验数据充分证明了代价敏感方法与其他方法相比，尤其是与代价不敏感原型相比，在降低分类总代价方面的有效性。

（2）针对不平衡数据集BCW和Ionosphere的G-means评价指标，本文方法明显好于Mc Mat MHKS，并且优于或者与Mat MHKS、MHKS相当。例如表4中，在Ionosphere上的G-means值约为Mc Mat MHKS的两倍。G-means值的提高表明代价敏感模型在少数类或者代价高的类别上的分类正确率有提升。

（3）从实验数据上看，矩阵形式不尽相同。有的在向量型数据上表现良好，有的在矩阵型数据上表现良好。这充分说明，针对最原始的向量型数据进行不同的矩阵变换是十分必要的。

（4）从图1中可以看到，Cs Mc Mat MHKS在Ecoli除第7、8类因仅有一个测试样本而数量太少影响不大外，其他多数类与少数类上的分类正确率均有所提高。

（5）从图2中可以看到本文方法均在有效次内收敛，证明了该算法具有较好的学习效率。

4　结束语

针对大多数实际问题中不同的分类会带来不同的损失，本文将代价敏感思想和相较于传统向量型学习机有更优性能的矩阵型学习机相结合，提出了矩阵型多类代价敏感分类器Cs Mc Mat MHKS。与代价不敏感的原型以及同一家族的分类器在数据集上的对比实验证明，本文方法可以有效降低错误分类总代价并提高分类器在少数类或者代价较高类别上的分类正确率，且可以快速收敛。实验证明，本文方法有着较优的分类性能，是一个有效且实用的模型。

［1］ ZHANG Yin，ZHOU Zhihua.Cost-sensitive face recognition ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（10）：1758-1769.

［2］ 叶志飞，文益民，吕宝粮.不平衡分类问题研究综述［J］.智能系统学报，2009，4（2）：148-156.

［3］ 杨明，尹军梅，吉根林.不平衡数据分类方法综述［J］.南京师范大学学报（工程技术版），2009，8（4）：7-12.

［4］ LI YUFENG，KWOK JAMES T，ZHOU Zhihua.Costsensitive semi-supervised support vector machine［C］// Proceedings of the National Conference on Artificial Intelligence.Atlanta，Georgia，USA：DBLP，2010：500-505.

［5］ SAHARE M，GUPTA H.A review of multi-class classification for imbalanced data［J］.International Journal of Advanced Computer Research，2012，2（3）：160-164.

［6］ 谷琼，袁磊，宁彬，等.一种基于重取样的代价敏感学习算法［J］.计算机工程与科学，2011，33（9）：130-135.

［7］ 程险峰，李军，李雄飞.一种基于欠采样的不平衡数据分类算法［J］.计算机工程，2011，37（13）：147-149.

［8］ DOMINGOS P.Metacost：A general method for making classifiers cost-sensitive［C］//Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.USA：ACM，1999：155-164.

［9］ 凌晓峰，SHENG VICTOR S.代价敏感分离器的比较研究［J］.计算机学报，2007，30（8）：1203-1211.

［10］ 闫明松，周志华.代价敏感分类算法的实验比较［J］.模式识别与人工智能，2006，18（5）：628-635.

［11］ 王瑞.针对类别不平衡和代价敏感分类问题的特征选择和分类算法［D］.合肥：中国科学技术大学，2013.

［12］ 程学云，吉根林，凌霄汉.基于SVM的多类代价敏感学习及其应用［J］.南京师范大学学报（工程技术版），2007，6（4）：79-82.

［13］ 李刚.代价敏感的支持向量机监督学习研究［D］.南京：南京师范大学，2007.

［14］ ZHOU Zhihua，ZHANG Minling，HUANG Shengjun，et al. Multi-instance multi-label learning［J］.Artificial Intelligence，2012，176（1）：2291-2320.

［15］ 付忠良.多分类问题代价敏感AdaBoost算法［J］.自动化学报，2011，37（8）：973-983.

［16］ 付忠良.多标签代价敏感分类集成学习算法［J］.自动化学报，2014，40（6）：1075-1085.

［17］ CHEN Songcan，WANG Zhe，TIAN Yongjun.Matrixpattern-oriented Ho-Kashyap classifier with regularization learning［J］.Pattern Recognition，2005，40（5）：1533-1543.

［18］ WANG Zhe，MENG Yun，ZHU Yujin，et al.Mc Mat MHKS：A direct multi-class matrixized learning machine［J］. Knowledge-Based Systems，2015，88：184-194.

［19］ 李勇，刘战东，张海军.不平衡数据的集成分类算法综述［J］.计算机应用研究，2014，31（5）：1287-1291.

［20］ RAUDYS S，RAUDYS A.Pairwise costs in multiclass perceptrons［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（7）：1324-1328.

［21］ LU Jiwen，ZHOU Xiuzhuang，TAN Yap-Peng，et al.Costsensitive semi-supervised discriminant analysis for face recognition［J］.IEEE Transactions on Information Forensics and Security，2012，7（3）：944-953.

［22］ TING Kaiming.An instance-weighting method to induce costsensitive trees［J］.IEEE Transactions on Knowledge and Data Engineering，2002，14（3）：659-665.

［23］ ASUNCION A，NEWMAN D.UCI machine learning repository［D］.California：University of California Irvine of Information and Computer，2007：148-156.

［24］ XU Qingsong，LIANG Yizeng.Monte Carlo cross validation ［J］.Chemometrics and Intelligent Laboratory Systems，2001，56（1）：1-11.

［25］ WANG Shuo，YAO Xin.Multiclass imbalance problems：Analysis and potential solutions［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2012，42 （4）：1119-1130.

Matrixized Multi-class Cost Sensitive Classification Mode

MENG Yun， WANG Zhe
（Department of Computer Science and Engineering，East China University of Science and Technology，Shanghai 200237，China）

At present，most of the classifiers are evaluated by classification accuracy，which assumes that all the misclassification costs are the same.Actually，different misclassification may bring different loss.Therefore，the cost sensitive learning has been becoming a hot research area in pattern recognition.By combining the cost sensitive and matrixized learning thoughts，this paper proposes a matrixized multi-class cost sensitive classification mode.The experimental results on the data show that the proposed method can reduce the classification costs and improve the classification accuracy of the minority or higher cost classes. Meanwhile，the proposed method has a better convergence，which illustrates the effectiveness and practice of the proposed method.

pattern recognition；cost sensitive；classifier design

TP391

A

1006-3080（2016）01-0119-06 DOI：10.14135/j.cnki.1006-3080.2016.01.019

2015-05-07

国家自然科学基金面上项目（61272198）；上海市教育委员会科研创新项目（14ZZ054）；中央高校基本科研业务费专项资金

孟 芸（1990-），女，河北保定人，硕士生，研究方向为模式识别。E-mail：mengyun_aijia@126.com

王 喆，E-mail：wangzhe@ecust.edu.cn