气动调节阀黏滞故障引起的回路振荡消除方法

张 昭， 张 亮， 夏春明（华东理工大学机械与动力工程学院，上海 200237）

气动调节阀黏滞故障引起的回路振荡消除方法

张 昭， 张 亮， 夏春明
（华东理工大学机械与动力工程学院，上海 200237）

气动调节阀的黏滞故障是控制回路中常见的故障，由黏滞引起的回路振荡将会破坏整个控制回路的性能。针对不具有定位器的阀门，提出了利用T-S型模糊控制器代替传统的PI控制器来消除此种振荡。该控制器利用阀门黏滞时被控对象的状态信息与控制器输出变化率之间的关系来构建模糊控制的规则。通过对传统PI控制器的积分系数进行修正使得阀门快速移出黏滞区，最终消除黏滞故障对回路的影响。将该算法应用于实际的液位控制回路中，实验结果表明该算法能够较好地消除回路的振荡，且能够适应不同的设定值，具有一定的鲁棒性。

气动调节阀；黏滞故障；回路振荡；T-S型模糊控制器；振荡消除

一个典型的过程工业工厂包含有成百上千的回路，这些控制回路的目标是保证工业过程在期望的环境下运行［1］。具有良好性能的控制回路会提高产品的质量、生产效率及安全性。性能差的回路，比如振荡，将破坏整个回路的控制性能和生产质量，造成大量的能源和原材料浪费［2］。气动调节阀是过程工业的控制回路中使用最为频繁的一类执行器件［3］，它的完好运行是回路良好控制性能的保证。然而工业调查［4-5］显示大约只有1/3的工业控制回路的性能是可以接受的，在较差性能的控制回路中有20%～30%的回路振荡是由于阀门中的黏滞故障引起的。阀门黏滞的存在使得控制回路产生极限环，控制变量处于振荡状态，而被控变量在设定值附近反复振荡［6］。因此如果能够尽快地减少或消除该故障对回路的影响，将具有很大的经济意义。

消除阀门黏滞故障对回路影响的最好方法是维修阀门或者更换一个性能较好的阀门。然而即使知道该故障在什么地方，由于是连续的生产过程，只有在工厂检修期间才能停车进行维护，而一般工厂的检修期为半年到三年不等［7］。如果能在线消除该故障对回路的影响，就可以增加回路的使用时间，最大限度地减少故障带来的损失。

针对阀门黏滞这一非线性故障对回路影响的消除方法，国内外的学者做了一定的研究。Hagglund提出了Knocker法［3］，即在回路的控制器输出信号中加入一个额外的补偿信号，该补偿信号由恒定幅度、宽度和时间间隔的脉冲序列构成。这种方法目前被认为较为合理，然而这种方式虽然减少了回路的输出波动，但却是以大幅度加大控制阀杆的运动为代价，也就是将回路输出的波动转移到阀门杆件，这样会导致阀杆的剧烈运动，加快了阀门的磨损。为了解决这一问题，Srinivasan在文献［8］中针对过程对象中无积分环节的回路使用两步法，较好地克服了过程的振荡，且避免了阀杆振荡的缺点。但该方法也存在不足之处：它需要回路振荡时的稳态信息（阀杆的位置、控制器的输出、被控变量的值等），在补偿的过程中不允许更改被控对象的设定值，而且使用的黏滞模型为单参数模型，实际过程很难满足这些条件。付川等［9］对Knocker迟滞补偿法进行了改进，对补偿信号设定一个阈值条件，即当控制器输出的变化超过一定阈值时，补偿信号才起作用，该方法在一定程度上降低了阀杆运动的次数。朱亚平等［10］在Knocker补偿算法的基础上，对控制器叠加的补偿信号的关键参数脉冲幅值进行自调整改进，提高了补偿算法的适应性，但始终没有克服Knocker补偿算法的阀杆磨损等缺点。周小伟等［11］在Srinivasan的两步法算法基础上提出一种基于过程对象的传递函数以及回路设定值的新型补偿方法，该算法可以消除回路的振荡，以及阀杆的来回移动，且能适应不同的设定值，具有一定的鲁棒性。但该算法只进行了仿真模拟，且算法所需的阀门实时位置信息有时不容易获取，限制了此算法的使用。

以上这些方法中存在的主要不足有：

（1）黏滞补偿的方法过度地依赖于黏滞的数据模型（模型黏滞参数固定不变）；

（2）黏滞补偿虽然使得被控变量能够达到设定值，但回路的其他环节中仍存在振荡，如控制器输出的振荡，这将明显加快阀门的磨损；

（3）补偿算法对不同的设定值的适应性较低。

因此基于阀门黏滞对回路的影响，希望实现以下3个目标：

（1）保证被控变量不会振荡且能够达到设定值；（2）保证控制器输出的稳定，以确保阀门不会出现来回的移动；（3）减少对黏滞参数的依赖性，且被控变量的设定值在一定范围内是可变的。

本文提出了一种新的消除气动阀门黏滞对回路影响的算法。该算法以T-S型模糊控制器代替原有控制回路中的PI控制器，利用阀门产生黏滞时被控对象的状态与控制器输出变化率之间的关系构建模糊控制的规则，通过修正积分项的作用，在无需获知控制对象模型的情况下消除阀门黏滞故障引起的回路振荡。

1　阀门黏滞

阀门黏滞是在阀门运行一段时间后，由于阀杆与填料之间的静摩擦力较大而引起的一种非线性故障，它是所有阀门故障中最为常见且最难克服的一种［12-13］。对于阀门黏滞，不同的学者和组织对其进行了定义，其中Choudhury等［14］的阀门输入输出S-J双参数模型为人们所广泛接受，该模型能够比较清晰地反映出黏滞出现时的物理特性。如图1所示，模型将执行器黏滞分为两个状态：最大静摩擦力大于滑动摩擦力引起的黏着阶段（Stick band and dead band）和阀门推力克服静摩擦力时的跳跃阶段（Slip jump），A～H为拐点，J和S为宽度。在A点和E点，控制器输出即阀门输入改变了方向（正向和反向），由于静摩擦力较大，阀杆将停止不动。为了克服静摩擦力，控制器的输出变化（AC或EG）必须达到宽度S，当到达C或者G位置时，阀杆开始运动，此时所受的摩擦力由较大的静摩擦力变为较小的动摩擦力，阀杆便跳跃（Slip jump）到一个新的位置D或者H，之后阀杆继续移动，如果在阀杆移动过程中速度较小，阀杆将可能会再次被黏住。

目前过程工业中大部分的控制回路采用传统的PID控制算法，特别是底层的单输入输出回路，大约90%都是PID控制回路［15］。在PID控制回路中，控制器需要反复调节才能达到某一设定状态，在此过程中控制器会不断地改变方向。当带有黏滞故障的阀门存在该回路中时，由上面的介绍可知，控制器改变方向阀门便发生黏滞，直到控制器的输出大于S时，阀杆才产生一个大小为J的跳动。而这样的一个跳动使得被控变量到设定值的另一侧，产生偏差。为了消除偏差，控制器将会再次改变方向，阀门将再次发生黏滞，如此反复，使得被控变量在设定值的附近反复振荡。在这个反复调节的过程中，PID控制器的积分作用是引起振荡的主要原因。

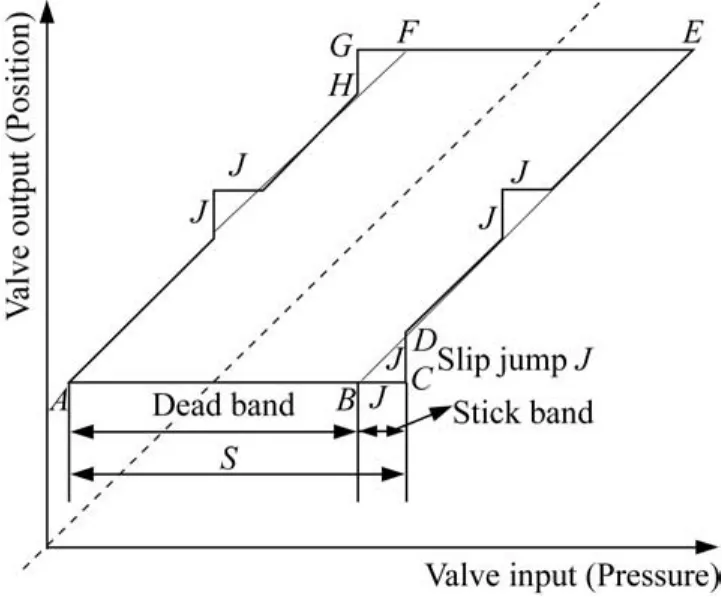
图1　黏滞阀门的输入输出关系图Fig.1 Sticky valve input-output behavior

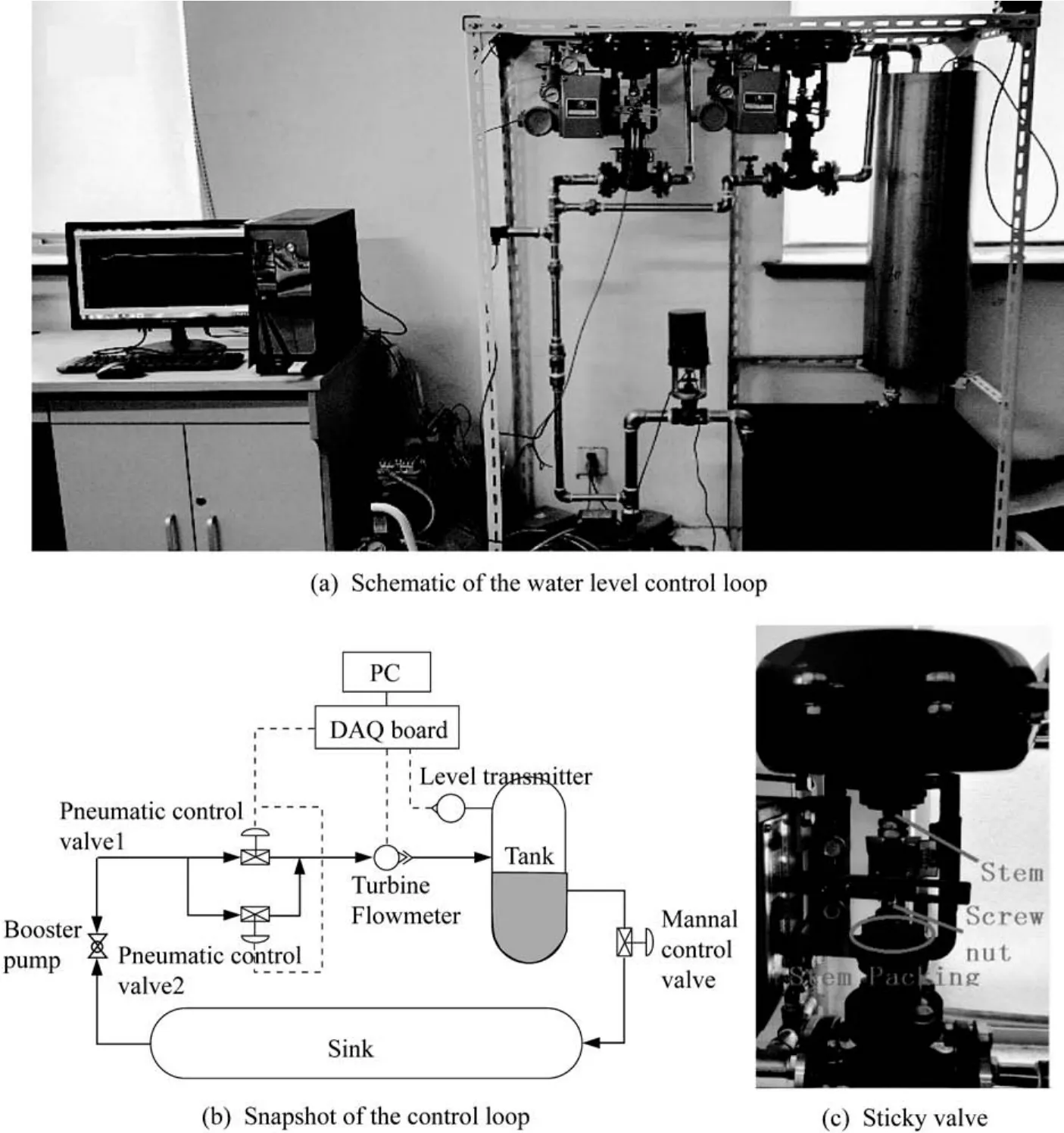
图2　实验装置Fig.2 Pilot plant

2　实验装置及条件

图2（a）示出了用于测试的实验装置，图2（b）和图2（c）分别示出了液位控制回路简图和黏滞阀门。实验平台主要用于单容水箱的PI液位控制，系统组成如下：选用德国威尔PUN-200E增压泵为系统提供动力，水源由一个方形蓄水池提供；控制回路中的执行机构为两个等百分比流量特性的气开式单座气动调节阀，型号为ZXP-DN15，气源由一台空气压缩机提供；型号为PT124B-22X的投入式液位变送器将水箱中0～800 mm的液位转化为4～20 m A的工业标准电流信号，并通过电压电流转换模块将电流信号转化为0～5 V的电压信号；电压电流转换模块将控制器输出的电压信号转化为4～20 m A的电流信号，电流信号作用在电流-气压转化模块上将电流信号转化为0～3 psi（0～20.684 kPa）的气压信号，用于推动阀杆的上下移动。LWGY型脉冲式涡轮流量传感器获取管道中的流量。利用研华的PCI-1710U采集板卡，完成Simiulink中Real-Time Window Target工具箱与外部器件的通讯，该板卡具有16路单端或8路差分模拟量输入（液位信号和流量信号），其中两路模拟量输出分别用于把控制器的输出施加在两个阀门上。液位信号和流量信号都经过了高斯滤波器的滤波处理，液位采样频率为1 Hz，控制器的输出频率为10 Hz，流量的采样频率为10 Hz。

装置中的两个阀门为线性度较好的阀门，对其中一个阀门通过拧紧螺母对密封装置增加紧固力，会增大阀杆与密封圈之间的摩擦力，这样阀门便会出现一定程度的黏滞故障。当阀杆在不同的工作位置时，通常S和J这两个参数是变化的，这也说明了依靠固定的黏滞参数的补偿算法是不太合理的，下面将通过开环实验来说明这种情况。

开环实验中施加的正弦信号的表达式如式（1）所示。

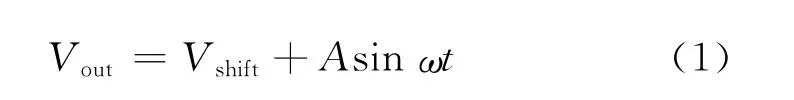
其中：Vout是施加的正弦电压；Vshift是提升电压，大小为2.5 V；A为正弦电压的幅度；ω为电压的频率，且大小为0.061 8 rad/s。为了说明在不同的工作点都存在黏滞现象，且黏滞的大小不同，A分别取值为0.5，1.0，1.5。图3为各种情况下的阀门输入和流量关系图，图中的数据都进行了归一化处理。图3（a）～3（c）中横轴代表时间，纵轴代表归一化后的数据。图3（d）～3（f）中Valve input代表正弦控制器的输出，Flow rate代表流量的大小（阀门的开度）。从图中可以看出当控制器输出信号的方向发生改变时，阀门都存在一定的黏滞现象，且正向和反向的黏滞大小不同。根据文献［15］中给出的阀门的输入输出关系图（图4），可以得到A在3种取值情况下阀门黏滞的参数，如表1所示。

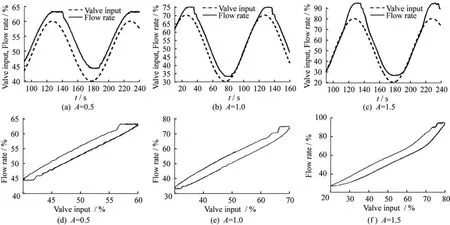
图3　归一化的阀门的输入与对应的流量关系图Fig.3 Normalized value input and corresponding normalized flow rate

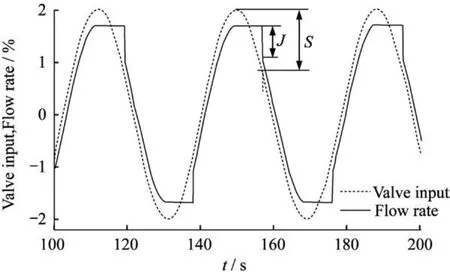
图4　黏滞阀门的输入输出序列图Fig.4 Input and output sequence of a sticky valve

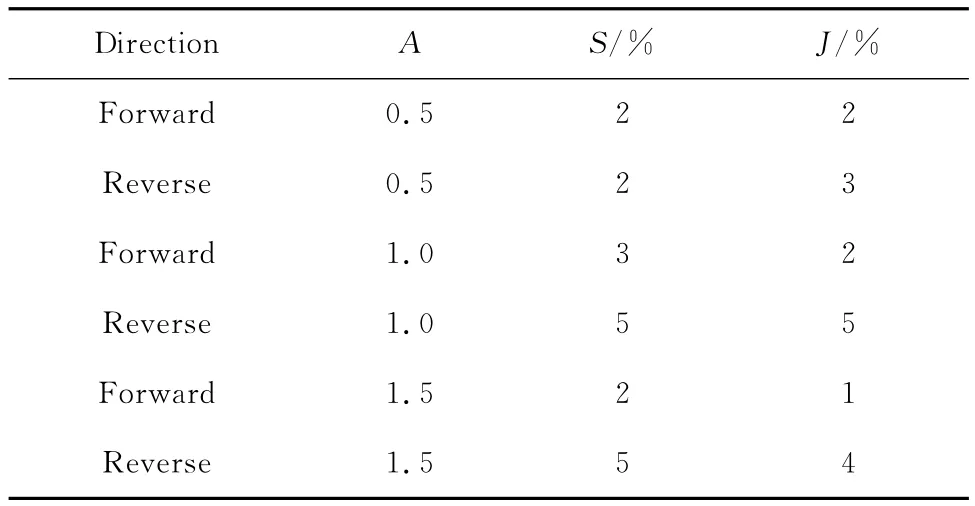
表13　种情况下的阀门黏滞参数Table 1 Parameters of the sticky valve underthree conditions

实验装置中有两个型号相同的气动调节阀，用于对比实验。将水箱底部的手动调节阀旋至一定的开度，用性能良好的阀门对水箱的液位作PI控制，然后在相同的参数设置下用黏滞的阀门代替性能良好的阀门。通过试凑法设置P（比例系数）和I（积分系数）两个参数，当P=1，I=0.01时，得到液位调节曲线如图5所示。从图5中可以看到，正常情况下经过大约600 s后液位输出基本上维持在2 V左右，当阀门存在黏滞时，被控液位在设定值附近出现了一定的振荡，这明显地降低了控制回路的性能。图6示出了控制器的输出曲线，可以看到控制器的输出大概以三角波的形式振荡，这将导致阀门阀杆来回移动，加快了阀杆的磨损。

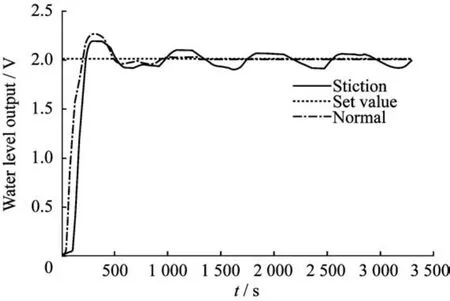
图5　正常与黏滞时PI调节曲线Fig.5 PI adjustment curve in normal and sticky state

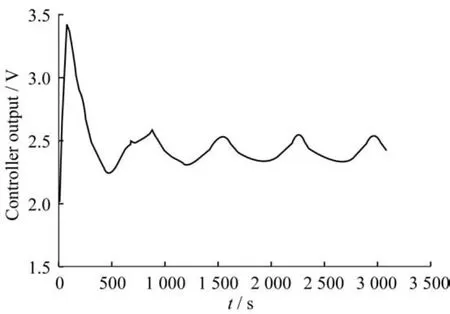
图6　黏滞时的控制器输出Fig.6 Controller output in sticky state

3　黏滞引起的回路振荡消除方法

对于传统的PI控制器，离散的PI表达式为

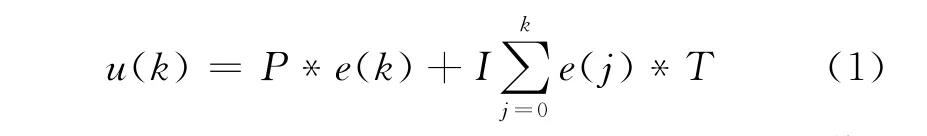
其中：e（k）=r（k）－y（k），r（k）为系统的设定值，y（k）为实际的输出值；P为比例系数；I为积分系数；T为采样周期。

由表达式可得控制器输出的变化率为

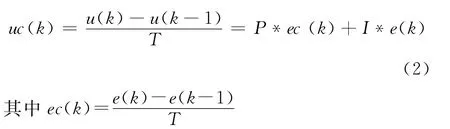
因此控制器输出的表达式可以转化为

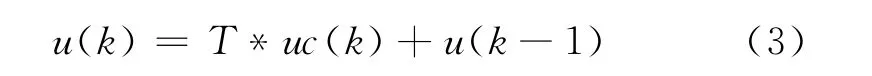
只要知道k时刻控制器变化率uc（k）的值和系统的采样周期T，便可以算出控制器的输出值u（k）。

在传统的PI控制作用中，当控制器改变方向时，是由于控制器的输出变化不够大，导致阀门出现了黏滞。因此我们可以在阀门出现黏滞时，通过改变积分项的作用，来改变控制器的输出变化率uc，进而加大或者减小控制器的输出，来快速地消除黏滞的影响。uc的大小对阀杆的运动有很大的影响，当阀杆黏住时，uc较大，可以帮助阀杆快速地移出黏滞区；当实际值将要达到设定值时，可降低uc的大小，避免被控变量产生一定的超调。阀杆的黏滞与否又与决定uc值的两个变量e（k）和偏差的变化率ec（k）有关。当e（k）≠0，ec（k）≠0时，说明此时被控变量没有达到设定值且还在不断发生变化，此时阀杆显然没有发生黏滞；当e（k）≠0，ec（k）=0时，说明被控变量没有达到设定值，它的大小不再发生变化，显然阀杆已经黏滞；当e（k）=0，ec（k）≠0时，被控变量还在不断地变化，阀杆没有发生黏滞；当e（k）=0，ec（k）=0时，说明被控变量达到设定值且不再变化，阀杆没有黏滞。针对以上情况，该模糊控制器的设计如下：

选取e和ec作为该控制器的语言变量。从图6中可以看到对于黏滞引起的振荡，被控变量只在设定值的附近小幅振荡。因此当回路出现因阀门黏滞引起的振荡时，误差e只在0的附近变化。这样e 和ec在论域上分别取两个隶属函数AZ和AFZ，下标Z代表0，FZ代表非0。各个语言变量选取高斯函数作为隶属函数，形式如下：

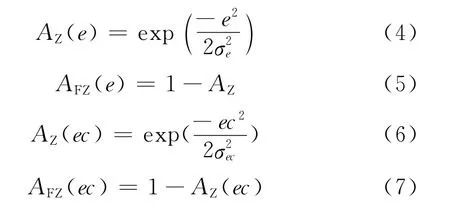
由以上分析，通过合理地改变积分系数I，调整控制器输出的变化率，可以使得阀杆跳出黏滞区。选取T-S型模糊推理模型，模糊推理输出为控制器的输出变化率uc。每个语言变量共有两个隶属函数和两个语言变量，这样便可以得到4条控制规则，控制规则如下：

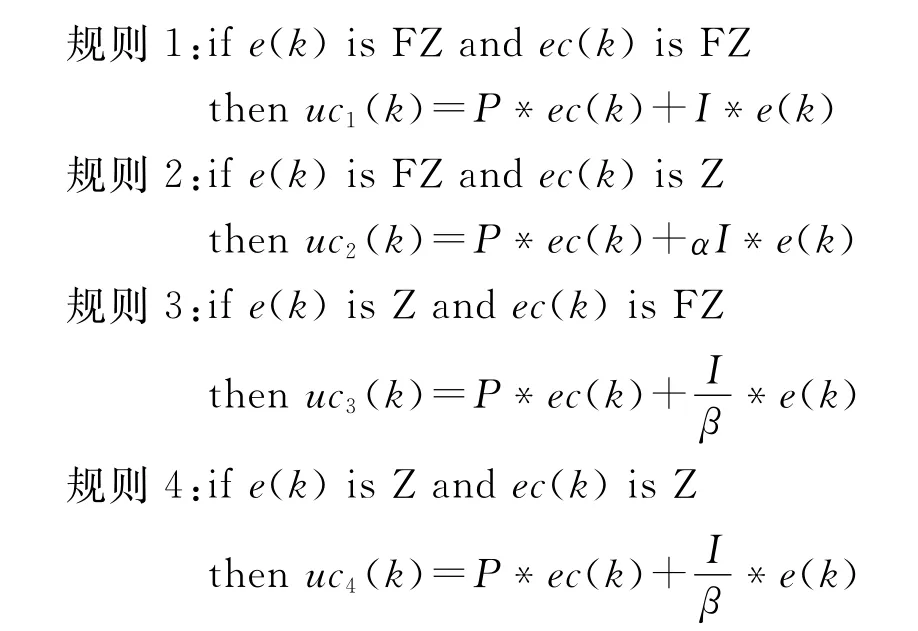
在规则1中，e（k）是非零，ec（k）也是非零，阀杆能够顺利移动，且被控变量没有达到设定值，不需要对I的系数作修正。在规则2中，e（k）是非零，ec（k）是零，阀门出现了黏滞，此时增大积分系数，使得阀杆能够快速地跳出黏滞区。修正因子a的取值为1.2～2.0，取值不能过大。在规则3中，e（k）是零，ec（k）是非零，被控变量已到设定值附近，阀杆能顺利地移动，被控变量还在变化，需减小积分系数防止出现超调，修正因子β的取值为2左右。在规则4中，e（k）是零，ec（k）也是零，被控变量已到设定值附近且被控变量还在作较小的变化，减小积分系数，减小控制器的输出变化，使被控变量能稳定在设定值上。

当模糊控制器的输入（e（k），ec（k））激活这4条规则时，模糊控制器的输出uc由这4条规则的输出uci（i=1，2，3，4）和每条规则所占的权重来决定。控制器的输出uc的表达式如下：

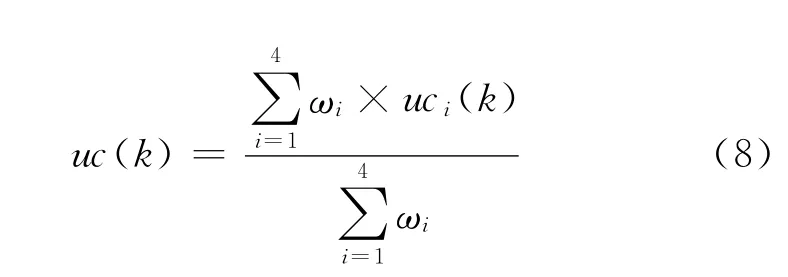
其中权重ωi的计算采用乘积法，计算表达式为

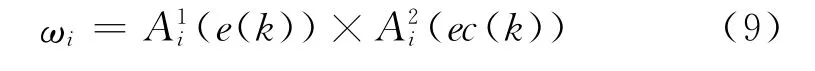
当计算出uc以后，采用式（3）就可以计算出用于控制阀门动作的控制量u（k）。

4　实验验证

为了验证所提出算法的有效性，在第2节给出的测试装置上进行实验。液位的设定值为2，控制器参数P、I为第2节中试凑法所取得的结果，即P=1，I=0.01。e的论域为［－2 2］，ec的论域为［－1 1］。高斯隶属函数的形状参数对该算法的效果有很大的影响，须保证它的取值使得在黏滞时的误差e是属于非零的情况。当黏滞发生时，e较小，须保证隶属函数的值大于0.5。从图5可看出，在振荡时，被控变量的误差约为0.15。因此当e取0.15时，AFZ（e）＞0.5，求得σe＜0.13，取σe=0.1。为了达到增强抗外界干扰的目的，取σec=0.01。此时e和ec的隶属函数曲线如图7所示。修正因子a取值为1.2～2.0，β取值为2。为了说明算法的效果和获得比较好的a，将通过a=1.0，1.2，1.5，2.0共4组实验结果来说明a的取值对控制结果的影响。

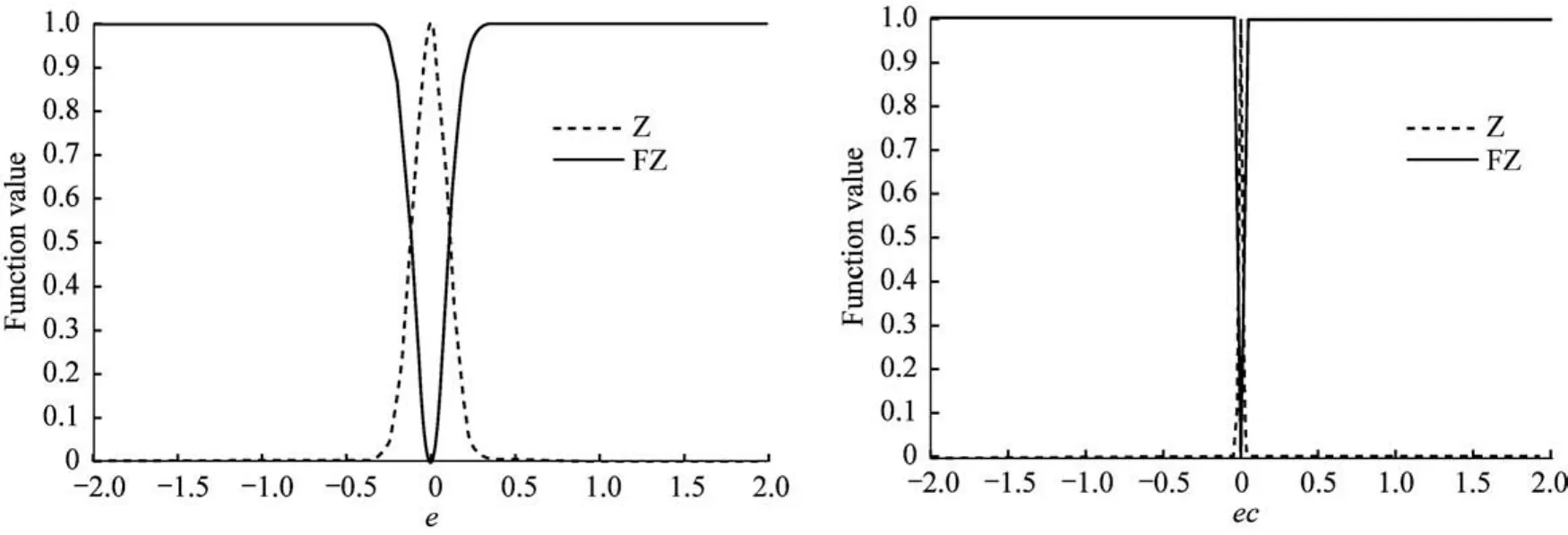
图7　e和ec的隶属函数曲线Fig.7 Membership function of e and ec

图8所示为a=1.0、1.2、1.5、2.0，β=2时得到的液位曲线。图8（a）只使用模糊控制器，没有对积分参数做任何修正，此时的液位和PI控制器控制下的液位都是在设定值附近来回振荡。图8（b）～图8（d）使用对积分项作修正的模糊控制器，可以看出，液位曲线在一段时间之后，基本上稳定在设定值2上。图9示出了液位偏差和偏差变化率，可以看出，e和ec的变化率也稳定在（0，0）平衡位置处，同样说明了液位能够较好地稳定在设定值上。图10示出了图8（b）～图8（d）3种情况下控制器的输出曲线，控制器输出最终都趋于一稳定值，因此阀门阀杆将不会再来回地移动，可以明显减少阀杆的磨损。在不同的情况下，液位的超调和趋于设定值的快慢是不同的，当a=1.2时，控制的效果比较理想；当a=1.5时，效果次之；当a=2.0时，超调较大，液位振荡的周期加长。因此选择a的取值范围为1.2 ～1.5，此次实验a=1.2，β=2，图11为该模糊控制器的输出uc与（e，ec）的关系图。

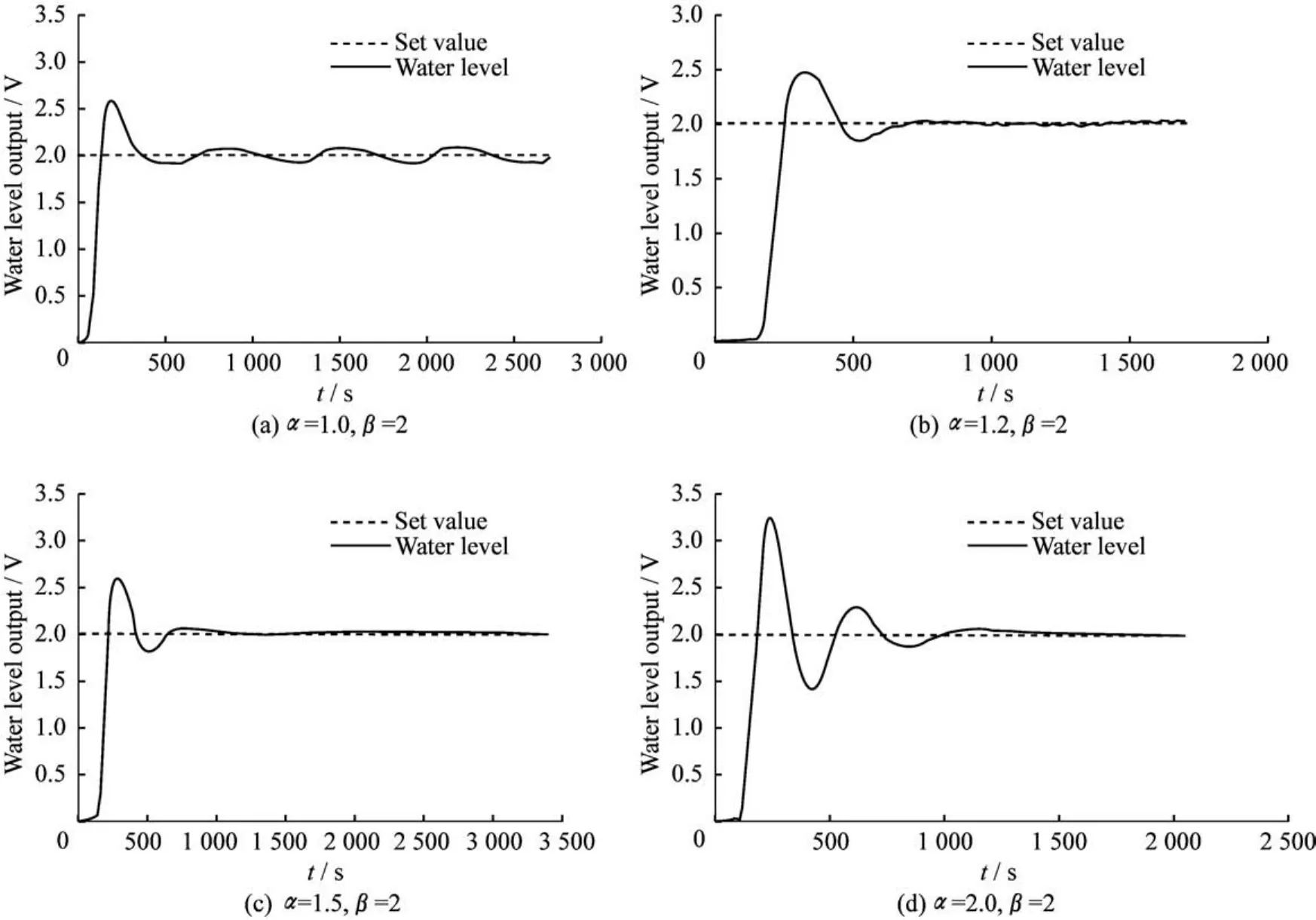
图8　黏滞补偿后的液位曲线图Fig.8 Level graph after compensation

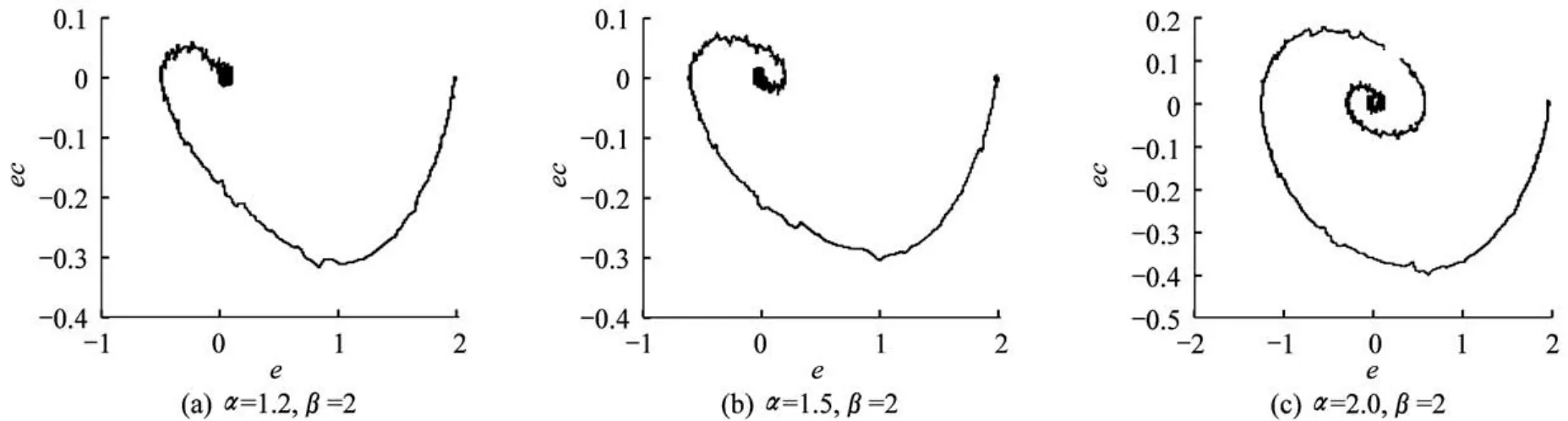
图9　液位偏差和偏差变化率曲线Fig.9 e vs ec curve

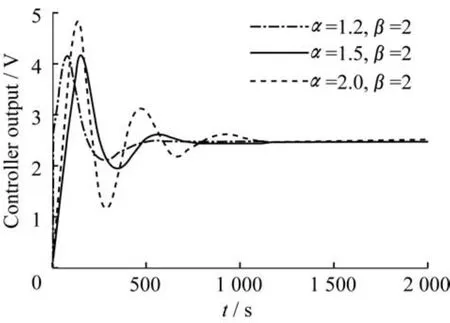
图10　控制器的输出曲线Fig.10 Controller output curve

一个性能较好的控制器，当在一定的范围内改变被控变量的设定值时，同样能够较好地工作而不需要重新整定控制器的参数。为了验证该控制器在改变被控变量的设定值后也能够消除黏滞故障对回路的影响，把液位由2 V变为3 V，实验结果如图12～13所示。从图12（a）中可以看到，在原有的PI控制器下，由于黏滞的存在，液位在设定值2 V附近反复振荡，当1 700 s时把设定值变为3 V，液位重新在新的设定值附近振荡。图12（b）使用了模糊控制器，可以看到，当设定值为2 V时，液位基本上稳定在设定值上，在2 000 s时把设定值变为3 V，液位稳定时有很小的波动，但与传统PI控制时的波动相比显著降低。从图13中可以看到，在不同的设定值下，传统的PI控制方法中的控制器输出是以三角波的形式反复振荡，使用新方法后，控制器的输出基本上比较平稳，阀杆不会来回地移动，降低了阀杆的磨损。由第2节中的开环实验可知，当阀门在不同的工作区工作时，黏滞大小的强度是不同的，而该控制器能够消除不同设定值处的黏滞故障对回路的影响，说明了它具有一定的鲁棒性。

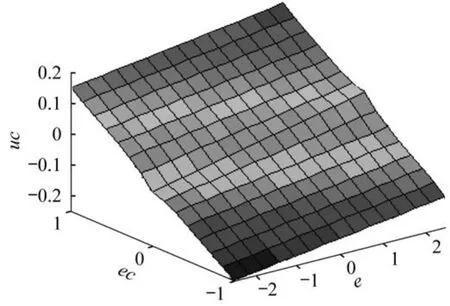
图11　模糊控制器的输出uc与（e，ec）关系图Fig.11 Relationship between the fuzzy controller output uc and（e，ec）

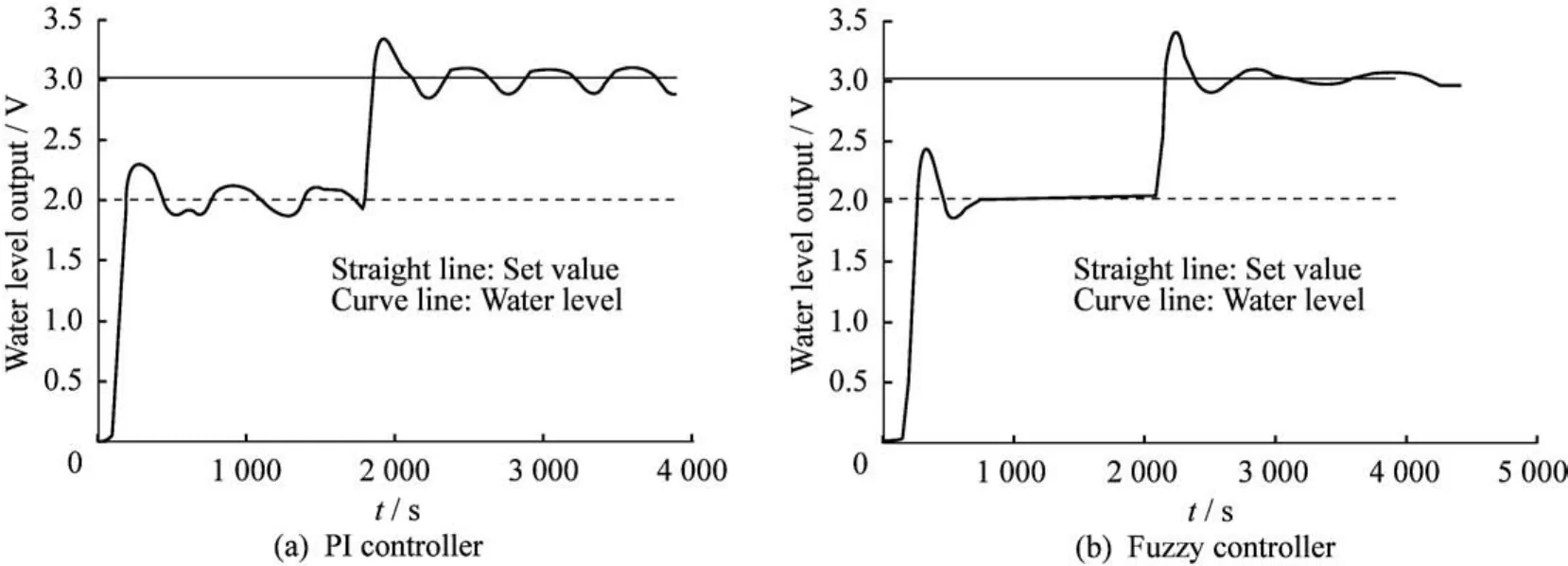
图12　设定值变化后的实验结果Fig.12 Experimental results after changing the set value

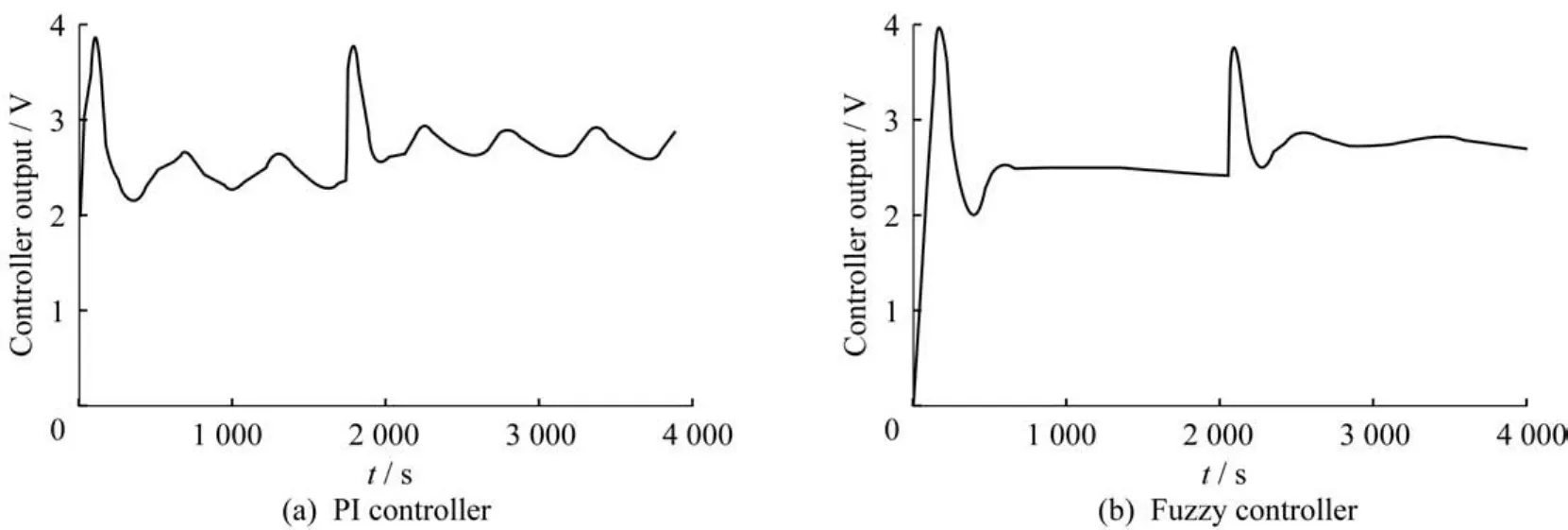
图13　设定值变化后的控制器输出Fig.13 Controller output after changing the set value

5　结 论

针对阀门的黏滞故障，提出了使用T-S型模糊控制器来消除由此故障引起的回路振荡。通过试凑法获取PI控制器的参数，然后把相同的参数赋予该模糊控制器，通过合理的参数修正来消除黏滞故障对回路的影响，降低了对被控对象模型的依赖性。由实验结果可以看出：

（1）控制器可以消除回路的振荡；

（2）被控变量能够稳定在设定值上；

（3）被控变量稳定后，控制器的输出也比较稳定，因此阀杆将不会来回地移动，明显地降低了阀杆的磨损，说明了该算法的有效性。

（4）从开环实验可知，阀门在不同的工作区，黏滞参数的大小是不同的。当改变被控变量的设定值，阀门在不同的工作区工作时，控制算法仍然可以较好地消除黏滞故障对回路的影响，说明了该控制算法具有一定的鲁棒性。

［1］ SEEM J E.A new pattern recognition adaptive controller with application to HVAC system［J］.Automatica，1998，34 （8）：969-982.

［2］ CHEN Li，SHOUKAT CHOUDHURY M A A，HUANG Biao，et al.Frequency analysis and compensation of valve stiction in cascade control loops［J］.Journal of Process Control，2014，24：1747-1760

［3］ HAGGLUND T.A friction compensator for pneumatic control valves［J］.Journal of Process Control，2002，12：897-904.

［4］ DESBOROUGH L D，MILLER R M.Increasing customer value of industrial control performance monitorings—Honeywell’s experience［C］//6th Internation Conference Chemical Process Control，AIChe Symposium.［s.l.］：［s. n.］，2002：169-189.

［5］ PAULONIS M A，COX J W.A practical approach for largescale controller performance assessment，diagnosis，and improvement［J］.Journal of Process Control，2003，13：155-168.

［6］ CUADROS MARCO ANTONIO de SOUZA L，MUNARO CELSO J，MUNARETO S.Improved stiction compensation in pneumatic control valves［J］.Computers and Chemical Engineering，2012，38：106-114

［7］ RANGANATHAN Srinivasan，RANGANATHAN Rengaswamy.Stiction compensation in process control loops：A framework for integrating stiction measure and compensation ［J］.Industrial&Engineering Chemistry Research，2005，44：9164-9174.

［8］ SRINIVASAN R，RENGASWAMY R.Approaches for efficient stiction compensation in process control valves［J］. Computers and Chemical Engineering，2008，32：218-229.

［9］ 付川，丁维明.控制回路中的阀门迟滞补偿方法［J］.自动化仪表，2010，31（10）：8-11.

［10］ 朱亚平，夏春明，张亮.阀门黏滞在线检测及黏滞补偿的KNOCKER方法改进研究［J］.液压与气动，2014（8）：41-48.

［11］ 周小伟，张亮，夏春明.控制回路中阀门黏滞故障补偿的一种新方法［J］.信息与控制，2013，42（6）：664-669.

［12］ KANO M，MARUTA H，KUGEMOTO H，et al.Practical model and detection algorithm for valve stiction［C］// Proceedings of the IFAC Symposium on Dynamics and Control of Process Systems.Boston，USA：［s.n.］，2004：859-864.

［13］ SRINIVASAN R，RENGASWAMY R，NALLASIVAM U，et al.Issues in modeling stiction in process control valves［C］// American Control Conference.Washington，USA：IEEE，2008：3374-3379.

［14］ CHOUDHURY M A A S.Diagnosis of Process Nonlinearities and Valve Stiction［M］.Heidelberg：Springer-Verlag，2008.

［15］ 周小伟.基于DAMADICS黏滞故障的建模与补偿平台的阀门故障分类及典型黏滞故障的建模与补偿［D］.上海：华东理工大学，2012.

Elimination Method for the Stiction Induced Control Loops Oscillation

ZHANG Zhao， ZHANG Liang， XIA Chun-ming
（School of Mechanical and Power Engineering，East China University of Science and Technology，Shanghai 200237，China）

Pneumatic valve stiction fault is often a common problem in control loops，and stiction induced oscillation is the main cause of poor performance in control systems.For valves without a positioner，this paper proposes the use of T-S type fuzzy controller instead of the traditional PI controller to eliminate such oscillations.When the valve is sticky，using the relations between the status information of the controlled object and the change rate of the controller output to build the fuzzy control rules.Adjust the integrator coefficient of traditional PI controller so that the valve can quickly get out of the sticky area and eventually eliminate the impact of stiction on the control loop.The actual level control results show that the compensation algorithm can eliminate control loops oscillation well and the controller is robust enough to adapt to different set values.

pneumatic valve；stiction fault；loops oscillation；T-S type fuzzy controller；oscillation elimination

TP273.2

A

1006-3080（2016）01-0132-09 DOI：10.14135/j.cnki.1006-3080.2016.01.021

2015-04-28

张 昭（1987-），男，硕士生，研究方向为气动阀门故障诊断及补偿。E-mail：zhangzhao7993@163.com

夏春明，E-mail：cmxia@ecust.edu.cn