基于三种亚格子模型的空腔振荡流动计算

白海涛， 赖焕新（华东理工大学承压系统与安全教育部重点实验室，上海 200237）

基于三种亚格子模型的空腔振荡流动计算

白海涛， 赖焕新
（华东理工大学承压系统与安全教育部重点实验室，上海 200237）

使用三种亚格子应力模型，对长深比（L/D）为5的三维矩形开式空腔的可压缩流体进行大涡模拟计算。研究得到的空腔自激振荡频率与Rossiter公式计算结果和实验结果吻合良好，结果显示振荡能量主要集中在较低频率区域，压力幅值主要出现在前三阶模态。Dynamic Smagorinsky-Lilly（DSM）模型在空腔前后壁面附近区域的脉动强度分布比Smagorinsky-Lily （SM）模型更为接近实验值，Wall Adapting Local Eddy Viscosity（WALE）模型的脉动强度分布与实验值最为接近。由空腔底部监测点声压级分布及声压频谱图可以看出：WALE模型性能最佳，DSM模型结果也与实验结果相符合，SM模型的预测性能略差。

开式空腔；自激振荡；大涡模拟；亚格子应力模型；气动噪声

流体流过物体表面的空腔或缺口时，由于腔外剪切流与腔内流动的相互作用，会出现自激振荡现象，同时出现剧烈的压力、速度脉动，并辐射产生强烈的噪声，该物理现象称为空腔自激振荡。空腔自激振荡现象广泛存在于飞行器的起落架舱、武器舱及燃烧室等部位，是典型的声-涡干涉、非定常流和流体动力不稳定问题。从20世纪50年代开始，人们对空腔自激振荡流动特性做了大量研究。关于开式空腔自激振荡物理机制，虽然有多种解释，但最被人们接受的是Rossiter［1］提出的空腔流声共振反馈模型并给出了预估振荡频率的半经验公式，该公式在一定精度范围内能够较为准确地预测空腔流激振荡的峰值频率，成为评价数值模拟结果的重要标准。

随着计算流体力学的发展，空腔声学特性的数值研究得到广泛开展［2］。湍流直接模拟（DNS）能够分辨所有能量尺度的涡，但目前局限于低雷诺数的情况。雷诺平均（RANS）能够较为准确地预测前几阶模态频率，但由于平均方法抹掉了湍流脉动部分信息，对于脉动强度的预测存在偏差。大涡模拟（LES）使用网格尺度的空间平均和滤波，可以保留大尺度涡运动湍流瞬态信息［3］，是目前被认为最有前景的数值方法。目前被广泛应用的亚格子湍流模型有Smagorinsky-Lily（SM）模型、Dynamic Smagorinsky-Lilly（DSM）模型和Wall Adapting Local Eddy Viscosity（WALE）模型。SM模型［4］适用于各向同性的湍流流动计算，因为形式简单，应用方便而得到广泛使用。湍流在黏性底层的脉动很小，相应的雷诺应力也很小，而壁面附近速度梯度却很大。此时，在壁面附近SM模型产生过大的耗散，尤其在边界层转捩问题中，往往抑制了转捩的发生或导致流动重新层流化［5］。为了弥补SM模型的缺陷，Germano等［6］提出DSM模型，通过建立随着时间与空间变化的亚尺度黏性系数公式，给出固体壁面上正确渐进关系，并能预测能量逆向传递因而得到更广泛关注。Moin等［7］于1991年将DSM模型应用于可压缩湍流。然而，DSM模型在某些流场中会得到不合理亚格子黏性系数［8］。Nicoud等［9］于1999年提出WALE模型，该模型采用速度梯度张量的平方，除了变形率张量，还考虑了旋转张量的影响，在近壁面尺度下可以较好得到涡黏性。

虽然前人在空腔自激振荡方面做了很多工作［10-11］，但迄今为止，关于不同亚格子模型在预测空腔自激振荡方面的差异鲜见报道。本文采用SM、DSM和WALE三种亚格子模型对空腔自激振荡流动特性和振荡机理进行分析，并将模拟计算结果与实验结果进行对比，分析这三种亚格子模型的优劣，为进一步研究空腔自激振荡发声机理提供参考和借鉴。

1　研究对象及网格

本文研究对象是M219三维矩形空腔［12］，长深比L/D=5。因为该空腔底部不会出现剪切层再附着情况，按照空腔静态流动特性［13］，该空腔为开式空腔。自由来流马赫数为M=0.85，进口滞止压力p0=100 996 Pa，滞止温度T0=309.3 K，对应的自由流速度U∞=280.2 m/s，基于空腔长度的雷诺数ReL=6.8×106。计算区域由空腔和空腔上方主流区域两部分组成，坐标原点在空腔底板中心处，主流区长（L′）、宽（W′）、深（D′）分别平行于空腔长（L）、宽（W）、深（D）。对整个流体区域划分结构网格，网格采用分区划分和局部加密技术，离壁面近处稠密，远离壁面稀疏［2］。模型尺寸及网格分布情况如表1和图1所示，表1中Y＋表示第一层网格到壁面距离的量纲为一量，用来考察网格质量的优劣。

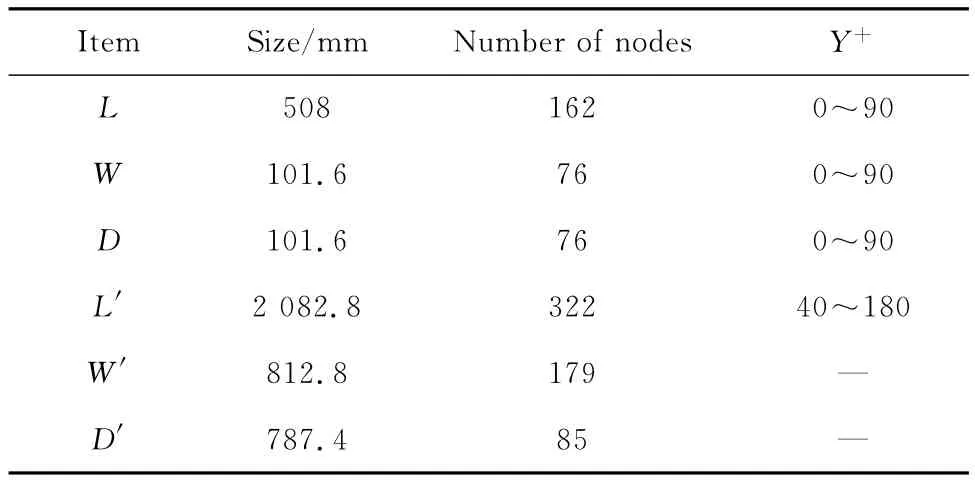
表1　模型尺寸及网格参数Table 1 Model size and mesh parameters

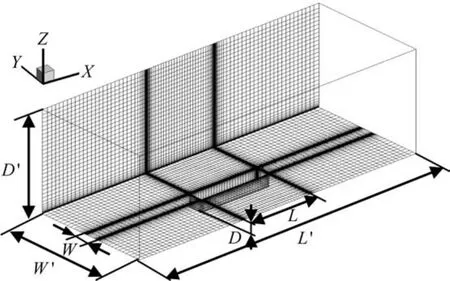
图1　计算区域及网格分布情况Fig.1 Computational domain and distribution of the grid

在空腔底板Y=－25.4 mm的线上均匀分布P1～P10共10个监测点，点与点之间的距离为50.8 mm，10个监测点位置对应英国国防科技公司QinetiQ对该空腔进行压力脉动测量实验的监测点，各个监测点分布情况如图2所示。

图2　监测点分布Fig.2 Distribution of monitoring points

2　数值计算方法

2.1控制方程与方法

可压缩流动的连续方程、动量方程和能量方程的量纲为一形式如下：

其中：i，j分别表示沿x，y方向分量；ρ，t，u，p分别表示密度，时间，速度，压力；σ，ET，q，S分别表示正应力，总能量，热通量和源项；符号顶部“－”表示普通滤波变量；“～”表示Favre滤波变量。

参考进口自由流变量进行量纲为一化，参照长度为空腔深度。亚格子应力张量τij有如下定义：

采用Boussinesq假定，亚格子应力使用式（5）计算：

其中：μt为亚网格湍流黏性力；τkk为亚网格尺度各向同性的部分；δij为应变率；S—ij为应力张量的速率，定义为

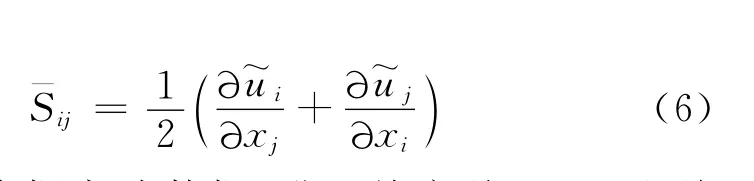
计算时依据实验数据，进口给定总温T0和总压p0，出口给出无反射压力边界条件，主流区前、后、上表面采用对称边界条件，其他面为无滑移固体壁面。使用Fluent软件计算流场，采用标准k-ε模型计算得到的稳态流场作为LES的初始场。LES模型中的亚格子湍流模型分别选取SM、DSM 和WALE模型，压力-速度耦合采用PISO算法，动量方程使用二阶迎风格式离散。时间推进步长为5×10－6s，相当于流体从流场流入到流出时间的1/1 488，计算总时长为0.3 s。

2.2三种亚格子（SGS）模型

SM模型是参照雷诺平均模式最早提出的SGS涡黏模型，以各向同性湍流为基础，认为亚网格湍流具有混合长度型涡黏系数：

1

DSM模型通过两个不同的亚尺度应变率张量，从已求解的区域信息计算得到Cs，Cs使用以下公式计算：

其中：Lij和Mij为二阶张量；k和h为常数；a为滤波宽度比为格子过滤尺寸，模型中的其他参数与SM模型计算方法相同。模型系数Cs在空间上的变化会导致计算不稳定，为了保证计算稳定，通常将模型系数在空间沿均匀流动方向进行特定的平均处理。

在WALE模型中，涡黏模型：

其中：Cw默认为0.325；gij为浮力产生项，其他符号与SM模型相同。WALE模型针对近壁面的流动，优化了亚网格黏性的计算方式，使预测结果更加符合真实的流动。

3　结果分析

3.1空腔的平均特性

图3给出了三种亚格子模型XOZ中心对称面平均流向速度和平均纵向速度分布情况。

图3中1.0＜Z/D＜2.0的区域表示主流区，三种模型的平均流向速度和平均纵向速度在主流区均吻合良好，表明了数值模拟的准确性。由于剪切流与腔内流动的相互作用，空腔内特别是空腔后壁面附近会出现剧烈的压力和速度脉动，涡黏模型的过分耗散会降低局部有效雷诺数［10］，导致各个亚格子模型在0＜Z/D＜1.0范围内的平均流向速度和平均纵向速度均有所差异。从总体上看，SM模型平均流速分布与DSM模型和WALE模型差异较大，主要是由于在空腔壁面附近存在强剪切作用，小尺度涡的强度会得到明显加强，导致涡的黏性耗散作用比SM模型给定的要强，从而出现了上述差异［14］。在流场复杂多变的空腔后壁面处，WALE模型的平均纵向速度表现出与SM和DSM模型的差异，是由于上游剪切层产生的涡核与空腔后壁面发生碰撞，变成碎片并表现出高度的不规则性，造成空腔后壁面处速度分布不具备严格的周期性［10］，因此，即使采样时间足够长，不同模型的采样时间平均值也会有一定差异。另一方面，本文LES采样时间可能还不够长，也是造成上述差异的原因。

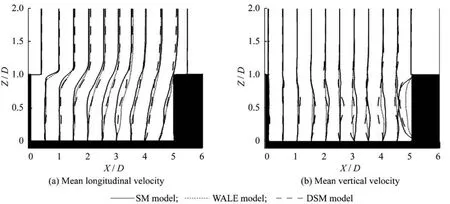
图3　XOZ中心对称面平均流向速度和平均纵向速度Fig.3 Mean longitudinal velocity and mean vertical velocity of the central XOZ plane

图4所示曲线为图2中10个监测点所在Y= －25.4 mm线上的声压级（SPL）分布情况，三种亚格子模型的预测结果都比实验值略高，是由于当用LES计算具有强剪切运动湍流时，常用的亚格子模型都会出现平均值偏高的现象［14］。自激振荡能量从空腔后壁面到前壁面大体上呈现单调递减分布，主要是因为空腔内的自激振荡由剪切层在空腔后壁面碰撞产生压力波，当压力波以涡旋的形式向上游运动时，一部分能量由于在空气中传播衰减而变弱，另外一部分能量在湍流运动中，由大尺度涡旋向小尺度涡旋逐级传递，直到有分子黏性起显著作用的尺度，并在该尺度下耗散为热能。因此，出现了下游自激振荡能量比上游大的趋势。

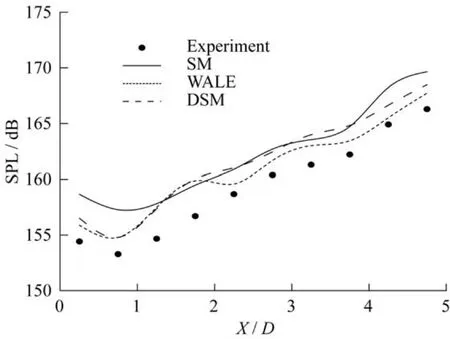
图4　空腔底部Y=－25.4 mm处声压级分布Fig.4 Sound pressure level distribution of Y=－25.4 mm in the bottom of the cavity

由SM模型与实验结果的对比情况来看，模拟值与实验值差别最大的地方是在空腔前、后壁面附近区域，在这两个区域，SM涡黏模型的过分耗散降低了局部雷诺数而使大尺度涡旋的预测结果比实验值偏大［15］。DSM模型由于动态计算CS，使得空腔前、后壁面处的声压级得到明显改善。WALE模型在空腔前半段与DSM模型预测结果一致，在后半段更加接近实验值，明显优于DSM模型，充分表现出其准确预测空腔底部声压级分布的优越性。

3.2空腔的瞬时特性

图5给出了空腔自激振荡已充分发展之后XOZ中心面一个周期（T）不同时刻的涡量等值线图。在0.25T，空腔前缘剪切层形成了一个脱落涡（图5 （a）），在0.50T～0.75T，脱落涡经过空腔中部继续向下游发展，同时涡旋强度不断加强（图5（b）～图5 （c）），一个周期结束时，第1个脱落涡与空腔后壁发生碰撞，碰撞后一部分涡沿着主流区向下游运动，另一部分沿着空腔后壁向空腔底部运动，此时空腔中下游区域产生剧烈的自激振荡现象，同时，空腔前缘剪切层又形成一个新的脱落涡（图5（d））。因此，空腔剪切层形成的具有一定脱落频率的涡与空腔内流场发生相互作用，产生复杂的非定常特性。

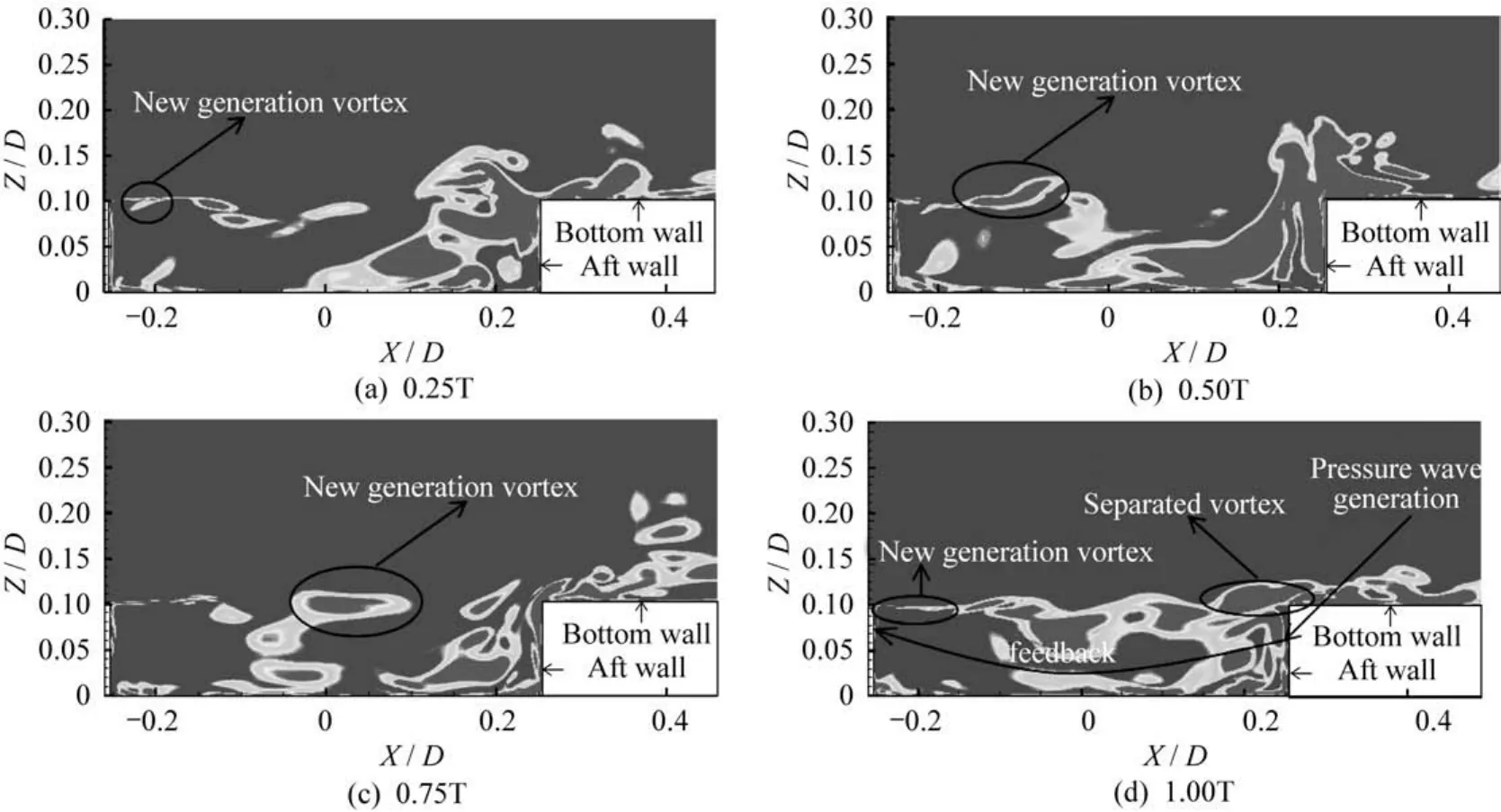
图5　空腔内瞬时涡量发展历程Fig.5 Instantaneous vorticity development in the cavity

采用Q准则可以对流场的涡结构进行识别和显示，定义为

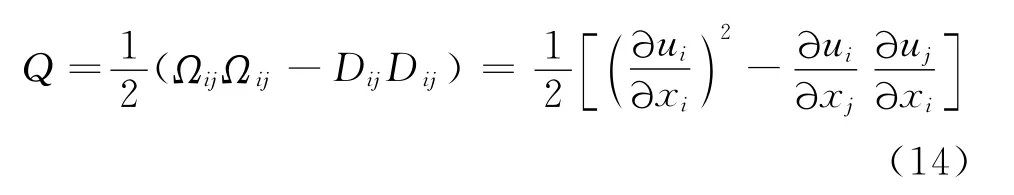
其中，Dij和Ωij分别为速度梯度的对称和反对称量，因此Q是速度矢量梯度的第二Halmiton不变量，Q等值面包络区定义了涡核分布情况。图6给出了使用Q指标等值面定义的涡结构。可以看出在空腔前方及展向区域都没有涡核的存在，由于Kelvin-Helmholtz作用，准周期性涡核在空腔前缘剪切层处产生并快速向空腔中下游发展，涡核不断变大，直至与空腔后壁面发生碰撞变成碎片并表现出高度的不规则性。

由图5中涡量等值线的变化历程及图6的涡结构情况，对空腔自激振荡机理分析：剪切层脱落涡与空腔后壁发生碰撞产生一次压力波，一次压力波向空腔前缘传播，扰动剪切层并激发剪切层更大的不稳定性，产生新的脱落涡，形成空腔自激振荡，完成一次反馈过程。

图6　Q指标定义的瞬时三维涡结构Fig.6 Instantaneous three-dimensional vortexstructure defined by Q criterion

在本文计算中，使用的工作站为3.0 GHz主频、20核心的DellTMPower EdgeTMT7610。计算表明在同样网格数目和相同边界条件下计算300个时间推进步长，SM模型需要40 min，DSM模型和WALE模型均需要41 min。因此可以看出这些模型在计算效率上没有明显差异。

经过三种亚格子模型计算，各个监测点的声压史被记录。由于瞬态计算的流场是一个由不稳定状态逐步发展到准稳态的过程，最终选用经过0.1 ～0.3 s达到准稳态的215个数据进行快速傅里叶变换（FFT）。实验采样时间为本文FFT变换采样时间的20倍，因此将实验数据均分为20段，图7中的实验值的压力频谱是20段数据的整体平均。图7将对空腔内有代表性的P1、P4、P7和P10进行重点分析。为清晰表明三种亚格子应力模型在预测空腔自激振荡方面的差异，在P10点分别列出三种亚格子模型结果与实验结果的对比，P1，P4和P7点处为综合对比。

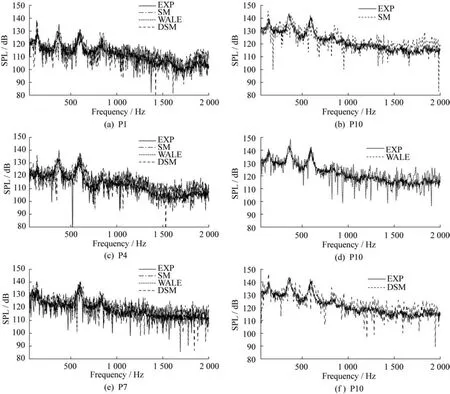
图7　声压频谱图Fig.7 Sound pressure spectrum

三种亚格子模型的模态频率和声压级与实验值吻合良好，都在合理预测范围之内。空腔自激振荡能量主要集中在0～1 000 Hz的低频区域，前三阶模态频率对应的声压级较大，是空腔自激振荡的主要振荡模式。在预测精准度上，三种亚格子模型仍有一定差异。表2、表3给出了P10点处三种亚格子模型前四阶模态频率及对应声压级与Rossiter公式和实验值的对比情况，括号内数值为计算值与实验值的相对误差。Rossiter公式如下：

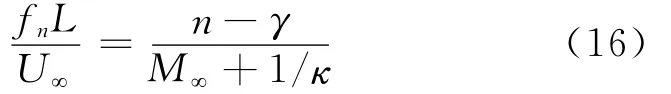
其中：fn为空腔振荡的模态频率，Hz；L为空腔长度，m；U∞为自由流速度；M∞为自由流马赫数；n为模态数；κ为涡速度与自由流速度比相关的常数，κ=0.57；γ为涡通过与产生声压之间的时间延迟因子，Lionel Larcheveque认为γ是与空腔长宽比相关的一个常数，当L/D=5时，γ=0.29［16］。

由表2和表3可以看出，若以3%相对误差为界限作为评价误差大小依据，SM模型的第一、二和第四阶模态频率预测偏差较大，而WALE模型的第二阶模态频率预测准确度较低。同时，SM模型和DSM模型的第一、四阶模态对应的声压级与实验值差别较大。上述差异也体现在P1、P4和P7这三个点上。因此，可以看出，由于SM模型采用单一的Cs常数，不能准确模拟有剪切流的固体壁面附近流动情况；DSM模型动态计算Cs常数的方法可以有效改善这一情况；WALE模型使用了正确的固体壁面流动的渐进行为，各监测点的声压频谱预测与实验值最为接近，表明WALE模型和DSM模型在预测监测点频率声压级分布方面要优于SM模型。

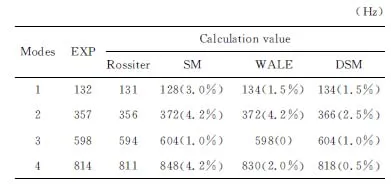
表2　P10点前四阶模态频率Table 2 Frequency of the first four modes at P10

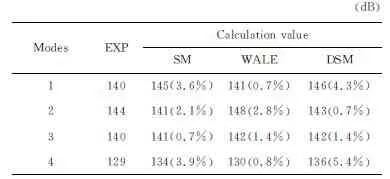
表3　P10点前四阶模态声压级Table 3 SPL of the first four modes at P10

4　结 论

本文使用SM、DSM和WALE三种亚格子模型对三维矩形空腔自激振荡流动进行大涡数值模拟，并与实验结果对比分析，得出以下结论：

（1）三种亚格子模型计算的前四阶模态频率与Rossiter公式计算结果和实验数据吻合良好，空腔自激振荡能量主要集中在0～1 000 Hz的低频区域，前三阶模态是主要的振荡模式，空腔自激振荡并没有严格的周期性。

（2）从计算的时间效率上来看，三种亚格子模型并无显著差异。由空腔底部监测点声压级分布及声压频谱图可以看出：WALE模型性能最佳，DSM模型也能给出与实验相符合的结果，SM模型的预测性能略差。

（3）由于WALE模型在近壁区域计算的优越性，相比SM和DSM模型，能更准确地预测空腔自激振荡的模态频率和压力幅值。该结果也间接说明亚格子模型对数值模拟结果的重要性。

［1］ ROSSITER J E.Wind tunnel experiments of the flow over rectangular cavities at subsonic andtransonic speeds［R］. London：Ministry of Aviation，1967：3438.

［2］ LARCHEVêQUE L，SAGAUT P，LE T H，et al.Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number［J］.Journal of Fluid Mechanics，2004，516：265-301.

［3］ GALPERIN A，ORSZAG S A.Large Eddy Simulation of Complex Engineering and Geophysical Flows［M］.USA：Cambridge University Press，1993.

［4］ SMAGORINSKY J.General circulation experiments with the primitive equations：I.The basic experiment［J］.Monthly Weather Review，1963，91（3）：99-164.

［5］ 邓小兵.不可压缩湍流大涡模拟研究［D］.四川绵阳：中国空气动力研究与发展中心，2008.

［6］ GERMANO M，PIOMELLI U，MOIN P，et al.A dynamic subgrid-scale eddy viscosity model［J］.Physics of Fluids A：Fluid Dynamics，1991，3（7）：1760-1765.

［7］ MOIN P，SQUIRES K，CABOT W，et al.A dynamic subgridscale model for compressible turbulence and scalar transport ［J］.Physics of Fluids A：Fluid Dynamics，1991，3（11）：2746-2757.

［8］ 周磊，解茂昭，贾明，等.不同亚网格尺度应力模型在燃油喷雾大涡模拟中的应用［J］.内燃机学报，2011，29（1）：29-35.

［9］ NICOUD F，DUCROS F.Subgrid-scale stress modelling based on the square of the velocity gradient tensor［J］.Flow，Turbulence and Combustion，1999，62（3）：183-200.

［10］ LAI Huanxin，LUO Kai.A three-dimensional hybrid LES-acoustic analogy method for predicting open-cavity noise［J］. Flow，Turbulence and Combustion，2007，79（1）：55-82.

［11］ XU Lan，CUI Guixiang，WANG Zhishi，et al.High accurate finite volume method for large eddy simulation of complex turbulent flows［J］.International Journal of Turbo and Jet Engines，2006，23（3）：191-210.

［12］ HENSHAW M J.M219 cavity case：Verification and validation data for computational unsteady aerodynamics［R］. ［s.l.］：British Aerospace（Operations）Ltd.，2000：453-472.

［13］ PLENTOVICH E B，STALLINGS R L，TRACY M B. Experimental cavity pressure measurements at subsonic and transonic speeds［J］.NASA Technical Paper，1993，3358：1-128.

［14］ 肖红林，罗纪生.大涡模拟中亚格子模型的改进及其在槽道湍流中的应用［J］.航空动力学报，2007，22（4）：583-587.

［15］ 赖焕新，周邵萍，罗开红.空腔的非定常可压缩过流及相关气动声学问题［J］.工程热物理学报，2007，28（5）：755-758.

［16］ LARCHEVÊQUE L，SAGAUT P，MARY I，et al.Largeeddy simulation of a compressible flow past a deep cavity［J］. Physics of Fluids，2003，15（1）：193-210.

Calculation of Oscillation Flow in Open Cavity Using Three Sub-grid Scale Models

BAI Hai-tao， LAI Huan-xin
（Key Laboratory of Pressurized Systems and Safety，Ministry of Education，East China University of Science and Technology，Shanghai 200237，China）

Three sub-grid scale models are employed to calculate the compressible fluid in a three dimensional rectangular open cavity，which has a length-to-depth ratio of 5.The frequencies of sustainedoscillation in the cavity are in agreement with experimental results and the Rossiter formula.The oscillating energy mainly concentrates on the low frequency areas.The first three modes are the basic frequencies of the flow induced oscillation.The main discrepancies of sound pressure level（SPL）occur in the areas near the fore and aft walls.The results of dynamic Smagorinsky-Lilly（DSM）model are more closer to experimental data than that of Smagorinsky-Lily（SM）model.The results of Wall Adapting Local Eddy Viscosity（WALE）model are the closest to the experimental data.The results of sound pressure level and sound pressure spectrum at the bottom of the cavity demonstrate that WALE model is the best one to predict the self-sustained oscillation of the cavity，while DSM model is fairly good，SM model is slightly inaccurate.

open cavity；self-sustained oscillation；large eddy simulation；sub-grid scale model；aerodynamic noise

O353.4

A

1006-3080（2016）01-0125-07 DOI：10.14135/j.cnki.1006-3080.2016.01.020

2015-05-08

国家自然科学基金（51576067）

白海涛（1989-），男，河南南阳人，硕士生，主要从事气动声学的研究。E-mail：bht119@126.com

赖焕新，E-mail：hlai@ecust.edu.cn