基于Abaqus的汽车发动机油底壳动力学性能优化

摘要： 为提升汽车发动机油底壳动刚度，减少其振动噪声，对其动力学性能进行优化.利用SolidWorks设计某型号油底壳初始模型，采用Abaqus分析其模态和频率响应，并根据分析结果对原始模型进行优化设计.优化后的汽车发动机油底壳结构动力学性能显著提升.

关键词： 汽车； 发动机； 油底壳； 刚度； 噪声； 模态； 频率响应； 优化

中图分类号： TB123；TK411.6文献标志码： B

Abstract： To improve the dynamic stiffness of an automobile engine oil pan and reduce its vibration and noise， its dynamic performance is optimized. An original oil pan model is designed by SolidWorks， the modal analysis and frequency response are analyzed by Abaqus， and the original model is analyzed and redesigned. The dynamic performance of the optimized automobile engine oil pan is enhanced significantly.

Key words： automobile； engine； oil pan； stiffness； noise； modality； frequency response； optimization

0引言

随着人类生活水平的提高，汽车已经成为众多家庭必备的出行工具.人们对汽车舒适性的要求越来越高，提高汽车舒适性能是汽车企业提高市场竞争力所要考虑的一个重要方面.汽车振动噪声严重影响乘员的舒适性.发动机噪声是汽车等机动车主要噪声来源，其薄壁构件之间相互振动和碰撞产生的辐射噪声占发动机总噪声的15%～20%，特别是油底壳与机体之间振动传递尤为显著.[1-3]研究发动机油底壳的动态力学性能，对于提高油底壳动刚度，减少振动辐射噪声，具有重要的现实意义.[4-5]

本文利用Abaqus对某型号发动机的油底壳进行模态分析和频率响应分析，找到原始设计的结构动刚度较小的部位，然后对其进行优化设计，以改善结构的动力学特性.

1动力学分析相关理论

1.1模态分析理论基础

模态分析可以分为解析模态分析和实验模态分析.用质量矩阵、刚度矩阵和阻尼矩阵分别表示结构的质量分布、刚度分布和阻尼分布，最终求得结构的模态参数称为解析模态分析.实验模态分析是利用实验仪器得到频响函数或者是脉冲传递函数，然后运用参数识别方法求得结构的模态参数.[6]本文利用解析模态分析方法来进行研究.

模态分析理论基本假设为线性假设、时不变假设和可观测性假设.根据这3种基本假设可知：模态分析实际上是将微分方程组中的物理坐标转换为模态坐标，解耦方程组，并使其变成仅以模态坐标和模态参数描述的方程，坐标变换的变换矩阵为振型矩阵，其每列即为各阶振型.由于模态变换属于线性变换，所以可以由各阶模态的叠加得到系统的动态响应，响应的大小取决于各阶模态的参与系数.通常，低阶模态的参与系数要高于高阶模态的参与系数，所以通常取前几阶模态叠加就可以得到系统的动态响应.[7-8]

考虑Mx¨+Kx=0（1）假设其解为x=eiωt（2）代入特征方程K-ω2M=0（3）或Δ（K-λM）=0（4）式中：λ=ω2

对于N自由度系统，有N个固有频率；与固有频率对应的特征向量称为模态振型；当结构振动时，在任意时刻，结构的形状为它的模态的线性组合.

1.2频率响应分析理论基础

频率响应分析是计算在稳态激励下结构动力响应的方法.在频率响应分析中，激励载荷是在频域中明确定义的，所有外力在每一个指定频率上是已知的.力的形式可以是外力，也可以是强迫运动（位移、速度、加速度等）.计算结果通常包括节点位移、加速度、单元力和应力等.

频率响应分析有两类不同的数值方法可以选择：直接法和模态法.直接法按照给定的频率直接求解耦合的运动方程；而模态法利用结构的模态振型来对耦合的运动方程进行缩减和解耦，同时由单个模态响应的叠加得到某一给定频率下的响应结果.

频率响应分析需要考虑以下几点[9]：

（1）如果激励的最高频率比系统的最低谐振频率小得多，那么做静力分析就足够了.

（2）阻尼很小的结构在激励频率接近于谐振频率时，会表现出很大的动力响应.在这样的响应问题中，模型上一个小的改动就可能产生响应上明显的变化.

（3）如果希望对峰值响应进行充分的预测，必须使用足够小的频率步长.对每个半功率带宽，至少需要使用5个点.

（4）为了得到最大的效率，应使用非均匀频率步长.在谐振频率区域使用较小的频率步长，在离开谐振频率的区域使用较大的频率步长.

2原始模型及其动力学分析

有限元模型是有限元分析中的基础，反映几何模型在实际工作过程中的受力情况和结构的力学关系，包括材料属性、外部载荷和约束等信息.油底壳有限元模型见图1.

有限元模型建立过程如下：

（1）所研究的油底壳是通过冲压工艺而成型的，结构的壁厚均匀，厚度为1.6 mm，在SolidWorks中建立油底壳几何模型，将三维几何模型导入Abaqus中，由于结构具有薄壁特征，采用壳单元进行分析精度很高，故需要提取结构中面，为有限元模型网格划分做准备.

（2）在油底壳实际工作过程中，法兰和机体下表面通过螺栓连接在一起，故对螺栓连接处的节点进行约束.

（3）油底壳材料为宝钢DC06钢材，弹性模量为2.06E+5 MPa，泊松比为0.3，密度为7.85E-9 t/mm.

（4）由于模型特征较多，故采用Abaqus/Standard求解器中的S4R和S3两种单元混合建模，其中S3起网格过渡作用.

2.1原始模型的模态分析

采用Abaqus/Standard求解器的Lanczos方法进行模态求解，提取结构的前100阶频率.该方法对模型规模较大，所提取振型较多时，求解速度更快.

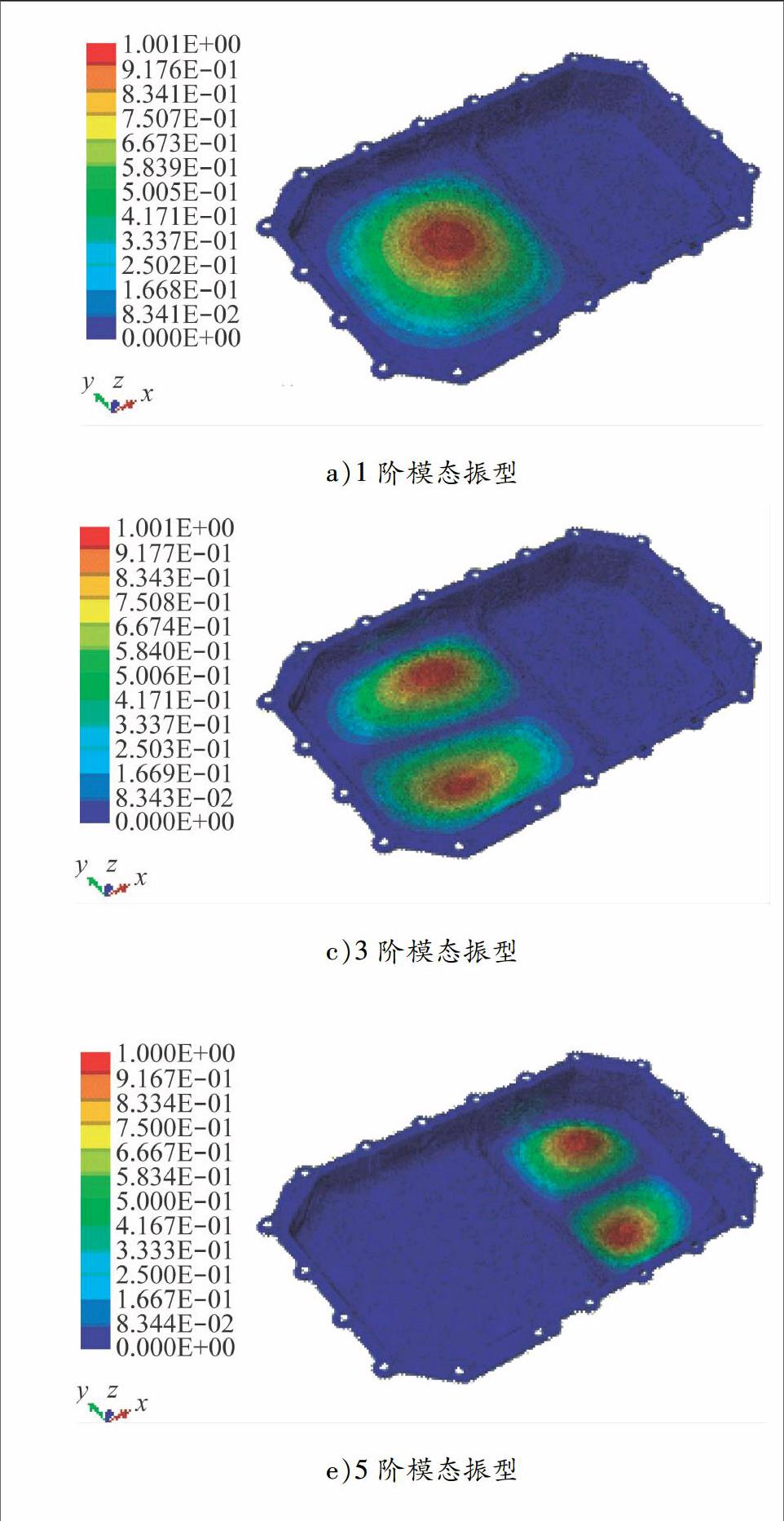
使用振型叠加法分析线性动态问题时，要保证频率提取分析步中提取足够数量的模态，以保证求解精度，判断标准为在主要运动方向上的总有效质量要超过模型中可运动质量的90%.[10]模型总质量为2.199 801E-3 t，由于受约束节点比例很小，可运动质量近似等于模型总质量，z方向为主要运动方向，有效质量为2.071 480E-3 t，占可运动质量的比例为94%.因此，提取100阶振型是足够的.原始模型前6阶固有频率见表1；原始模型的前6阶模态振型见图2.由图2可知前6阶振动主要在油底壳底部大平面区域.在设计过程中应该对底部区域进行加强处理，提高结构的振动性能.

2.2原始模型的频率响应分析

模态分析得到油底壳固有频率和振型，但是要进一步了解其动力学特性，需要进一步分析结构的频率响应.

实际工作中油底壳受到的激励是通过机体传递过来的，并且油底壳的刚度小于机体裙部，因此可以把油底壳和机体看成是非耦合系统[1-3].油底壳仅接受和机体连接的振动激励，因此可以在螺栓孔位置施加激励载荷.本文采用油底壳和机体连接处螺栓的多点垂向（z向）单位位移（1 mm）的激励来替代实际的激励，频率响应分析的频域范围为0～1 500 Hz，结构模态阻尼因子取0.06.以模态分析为参考，选取2个具有代表意义的点作为参考点.参考点位置见图3；两个观察点z方向位移响应见图4.结果表明：观察点1在289 Hz和852 Hz附近位移响应达到峰值，分别由第1阶和第6阶模态振型引起.观察点2在410 Hz和467 Hz附近位移响应达到峰值，由第2阶模态振型引起.

3优化后的模型及对比分析

由于该结构底部为大平面结构，通过以上分析了解到，结构的前几阶振动主要集中在底部，为增加底部刚度，在底部大平面加5根纵向加强筋，底部小平面加2根纵向加强筋和2个横向小凸台.以改善结构动力学性能.优化后的油底壳模型见图5.

对优化后的结构进行模态分析，对比原始模型固有频率，见图6.前6阶固有频率分别提升55.610%，41.750%，18.053%，63.857%，27.865%和16.524%，说明加强筋对结构整体刚度提升很大.

对优化后的结构进行频率响应分析，对比原始模型的z方向位移响应，见图7.

优化后的结构在两个观察点峰值响应出现时的频率远远大于优化前的结构，说明底部动刚度改善很大，与模态分析结论一致.

4结束语

对某型号发动机油底壳进行初步设计，从动力学角度分析结构的动刚度，找到结构较薄弱部位，对底部平面区域进行优化设计，增加7根加强筋和2个小凸台.优化后结构的动刚度改善很大，固有频率提升显著.在发动机不同频率的激励下，优化后的结构位移响应峰值相比原始结构在更高的频率点出现.该方法对油底壳的设计具有重要的指导意义.参考文献：

[1]方立桥. 油底壳加强筋和滚筋结构优化设计[D]. 北京： 北京交通大学， 2013.

[2]张海娟. 发动机油底壳振动与噪声辐射研究[D]. 合肥： 合肥工业大学， 2006.

[3]郑光泰. 发动机镁质油底壳开发振声特性研究及优化设计[D]. 浙江： 浙江大学， 2008.

[4]袁兆成， 张亮， 方华， 等. 4118Z型柴油机油底壳模态与结构分析[J]. 汽车工程， 2001， 23（3）： 156-159. DOI： 10.3321/j.issn：1000-680X.2001.03.004.YUAN Z C， ZHANG L， FANG H， et al. Modal analysis and structure analysis for oil-pan of 4118Z diesel engine[J]. Automotive Engineering， 2001， 23（3）： 156-159. DOI： 10.3321/j.issn：1000-680X.2001.03.004.

[5]倪伟. 发动机油底壳的设计探讨[J]. 内燃机与动力装置， 2012（2）： 51-53. DOI： 10.3969/j.issn.1673-6397.2012.02.014.

NI W. Discussion on engine oil pan design[J]. Internal Combustion Engine & Powerplant， 2012（2）： 51-53. DOI： 10.3969/j.issn.1673-6397.2012.02.014.

[6]崔宽. 含缺陷类桁架点阵夹芯结构振动性能分析[D]. 哈尔滨： 哈尔滨工业大学， 2014.

[7]曹树谦， 张文德， 萧龙翔. 振动结构模态分析： 理论实验与应用[M]. 2版. 天津： 天津大学出版社， 2014： 1-50.

[8]胡海岩. 机械振动基础[M]. 北京： 北京航空航天大学出版社， 2005： 1-6.

[9]田利思， 李相辉， 马越峰， 等. MSC Nastran动力分析指南[M]. 北京： 中国水利水电出版社， 2012： 1-74.

[10]石亦平， 周玉蓉. Abaqus有限元分析实例详解[M]. 北京： 机械工业出版社， 2006： 279-301.（编辑于杰）第25卷 第4期2016年8月计 算 机 辅 助 工 程Computer Aided EngineeringVol.25 No.4Aug. 2016