等离子体中的CDLT-Leapfrog-ADI-FDTD方法

成丹，殷红成，韦笑，郑宏兴

(　　　1.中国传媒大学信息工程学院，北京 100024；2.天津职业技术师范大学天线与微波技术研究所，天津 300222；3.电磁散射重点实验室，北京 100854)



等离子体中的CDLT-Leapfrog-ADI-FDTD方法

成丹1，2，殷红成3，韦笑3，郑宏兴2

(1.中国传媒大学信息工程学院，北京 100024；2.天津职业技术师范大学天线与微波技术研究所，天津 300222；3.电磁散射重点实验室，北京 100854)

采用电流密度拉普拉斯变换(CurrentDensityLaplaceTransform)方法将无子时间步的蛙跳式交替方向隐式时域有限差分(leapfrog-ADI-FDTD)方法应用于等离子体的电磁计算中，得到了等离子体中的迭代公式。为了验证该方法的有效性，计算了等离子体平板的反射系数和透射系数，并与几种传统的FDTD方法进行了对比，数值实验表明，提出的算法具有无条件稳定性，精度和效率高于普通的显式FDTD方法。

等离子体；蛙跳；时域有限差分方法；交替方向隐式

1　引言

等离子体在现代化工业的各个领域具有广泛的应用，其中飞行器再入大气层的跟踪识别和等离子体隐身技术是等离子体研究的两个重要方面[1]。两方面问题的关键在于对电磁波与等离子体相互作用的认识，因此研究等离子体的电磁特性具有重要的意义，一直受到国内外的广泛关注[2-5]。

时域有限差分(Finite-DifferenceTime-Domain，FDTD)方法是计算等离子体电磁特性的一种常用的数值方法，经过多年的发展，出现了大量的处理色散媒质电磁问题的FDTD算法，例如辅助方程(AuxiliaryDifferentialEquation，ADE)法[6]、移位算子(ShiftOperator，SO)法[7]、电流密度拉普拉斯变换(CurrentDensityLaplaceTransform，CDLT)法[8]等方法。其中，CDLT-FDTD法是利用等离子体介质中的电流密度矢量与电场强度的本构方程，将方程两边分别进行拉式变换，得到S域内的本构方程，再进行拉式逆变换和指数差分，得到在时域中的FDTD迭代方程，避免了处理频域本构关系到时域本构关系中的卷积问题，更为简单。

一般的FDTD方法受到Courant稳定性条件的限制，使得计算效率降低。为此，无条件稳定的交替方向隐式时域有限差分(ADI-FDTD)方法被引入到等离子体的电磁计算中[9-12]。因其时间步长不受Courant稳定性条件的限制，可以取的相对较大，较传统的FDTD方法提高了计算效率，但该方法存在中间的子时间步，在无条件稳定的同时损失了一定的计算资源。2009年Cooke等人提出了一种新的无条件稳定的蛙跳式交替方向隐式时域有限差分(leapfrog-ADI-FDTD)方法[13]，较传统的ADI-FDTD方法而言，该方法没有子时间步的计算资源消耗，迭代方程更为简单，但仍然保持了无条件稳定的优点，所以该算法相对传统的无条件稳定算法有更高的效率[14，15]。

本文将CDLT-FDTD方法与leapfrog-ADI-FDTD方法相结合，提出相应的混合算法，给出推导过程和迭代公式。本文算法很容易推广到其他普通媒质或有耗色散媒质的电磁计算中，可扩展性强。通过与其它FDTD方法对比，采用算例验证了本文方法的有效性。

2　CDLT-Leapfrog-ADI-FDTD算法推导

各向同性、非磁化、碰撞等离子体中，麦克斯韦方程组和相关方程为：

(1)

(2)

(3)

式中，E为电场强度；H为磁场强度；J为极化电流密度；ε0μ0分别为真空中的介电常数和磁导率；ν为等离子体碰撞频率；ωp为等离子体角频率。将(3)式经拉氏变换，再反变换回时域可得：

(4)

其中，J0为初始时刻的电流密度，可见处理以后的(4)式中不包含微分项，所以在离散时不必做差分近似，从而提高了精度。下面以Ex为例说明(1)、(2)、(4)式中CDLT-Leapfrog-ADI-FDTD方法的迭代公式。

子时间步t=nΔt到t=(n+1/2)Δt时刻的Maxwell旋度方程中的Ex、Hz和Jx离散的迭代公式为

(5)

(6)

(7)

将式(6)和(7)带入(5)中可得

(8)

子时间步t=(n+1/2)Δt到t=(n+1)Δt时刻的Maxwell旋度方程离散的迭代公式为

(9)

(10)

(11)

将式(9)、(10)、(11)分别回退一个时间步可得

(12)

(13)

(14)

将式(13)和(14)整理后带入(12)中，再带入(8)中可消去Ey，得到Ex的最终迭代式

(15)

类似可得到相应的其他电磁场分量的迭代式。电场和磁场的参数矩阵均在整时间步上迭代，且为三对角条带矩阵，可采用追赶法求解。

将(7)带入(11)中，即可得到x方向电流密度迭代式：

(16)

类似可得到其它电流密度分量得迭代式。可见，CDLT-Leapfrog-ADI-FDTD是一种没有中间子时间步的交替隐式时域有限差分方法，而且电磁场均采用隐式计算，稳定性和计算效率将优于其他隐式方法。

3　算例验证

为了验证本文算法的有效性和性能，分别用ADE-FDTD、SO-FDTD和本文的方法计算了等离子平板的反射系数和透射系数。等离子体平板的厚度为1.5cm，碰撞频率和角频率分别为ν=20GHz，ωp=2π×28.7Grad/s，计算空间步长Δd为75μm，前两种方法时间步长Δt=0.125ps，本文方法时间步长为ΔtL，为了方便讨论定义CFLN=ΔtL/Δt，这里取CFLN=4。入射电磁波为高斯脉冲，整个计算空间为800个网格，等离子体平板占据中间200个网格，其余为真空。计算空间边沿使用采用一阶Mur吸收边界吸收不必要的反射。

图1给出了四种方法计算的电磁波通过等离子平板的反射系数和透射系数振幅，并与相应的解析解进行比较。其中前三种方法因时间步长的限制，计算20000步才达到较好的收敛状态，即使这样，SO-FDTD方法在计算透射系数时，0到20GHz范围的值仍存在振荡，与解析解有较大偏差，其余方法与解析解基本吻合。本文方法因其无条件稳定性，所取时间步长为其他FDTD方法的4倍，计算进行6000步即收敛，如图1所示。为了验证这一点，本文给出几种方法入射点电场随时间的变化规律和另外两种方法计算6000步时的透射系数振幅，分别如图2和图3所示。由图2可知，本文方法收敛速度显然优于其他两种方法。图3中的透射系数振幅的计算结果反映出两种一般方法计算6000步时，在0到20GHz范围内均严重偏离解析解，而本文方法则与解析解吻合。

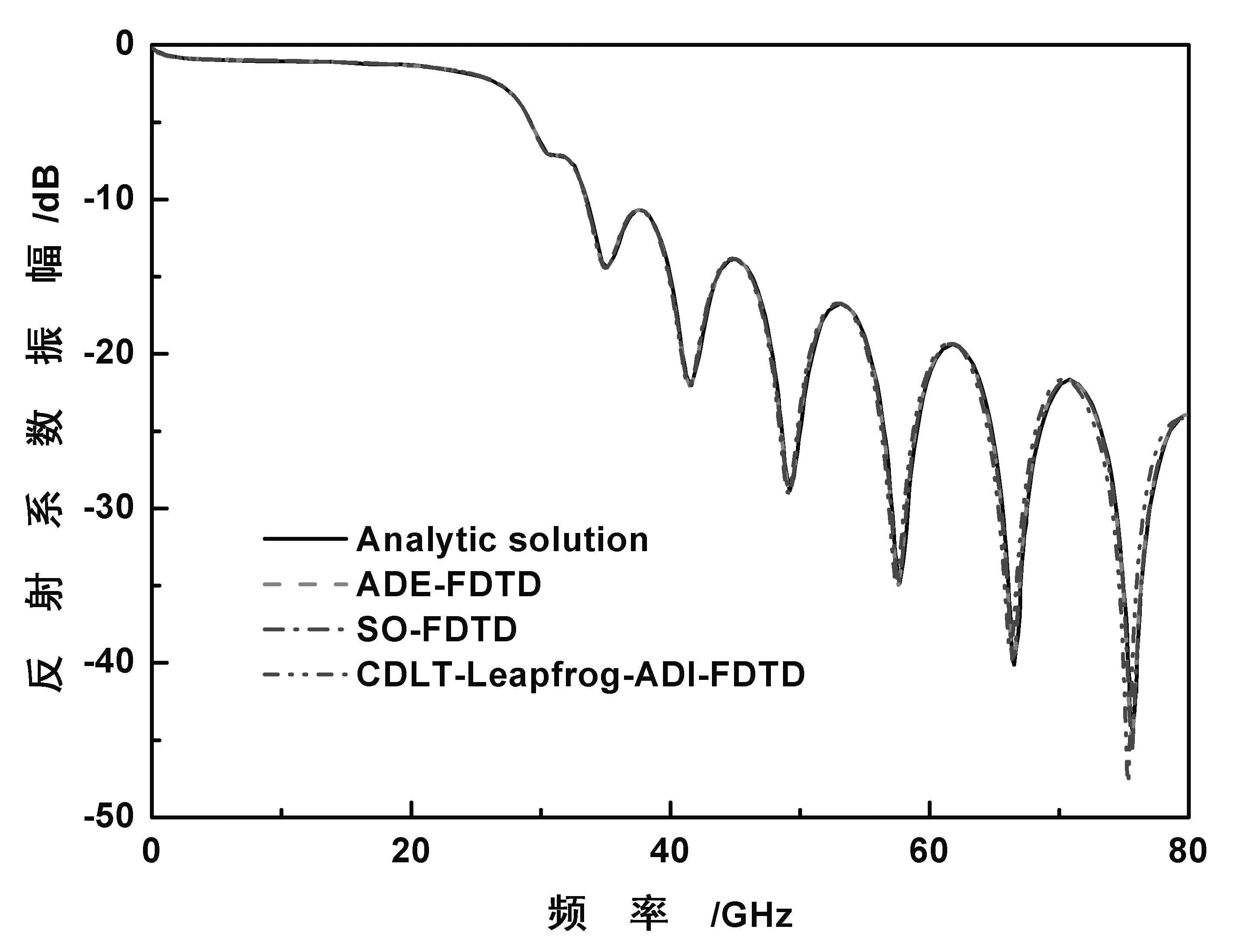
(a)反射系数振幅　

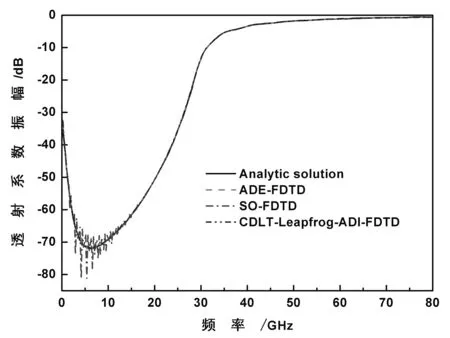
(b)透射系数振幅图1　电磁波通过等离子平板的反射系数和透射系数振幅随入射波频率的变化　

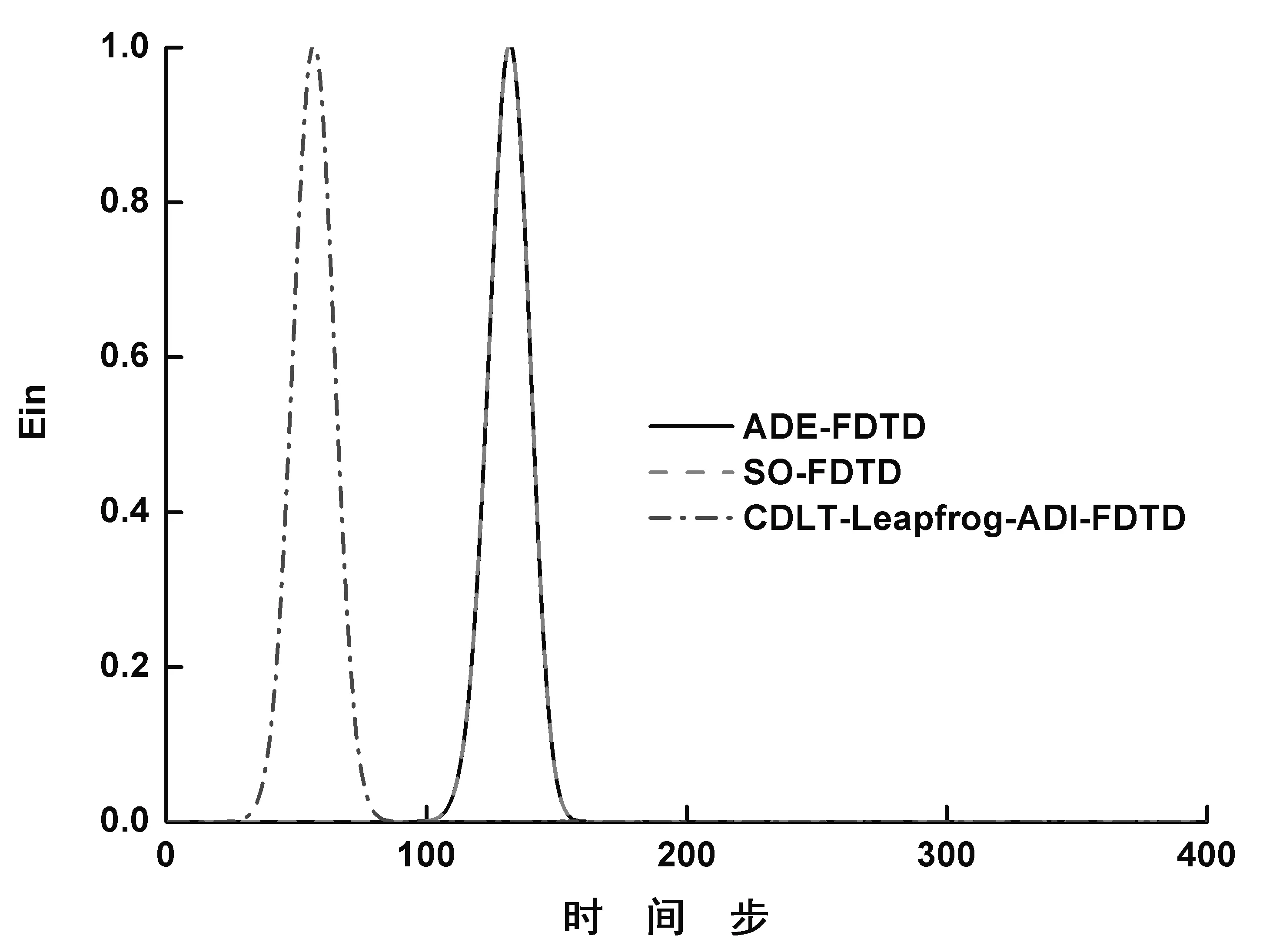
图2　三种FDTD方法入射波随时间的变化　

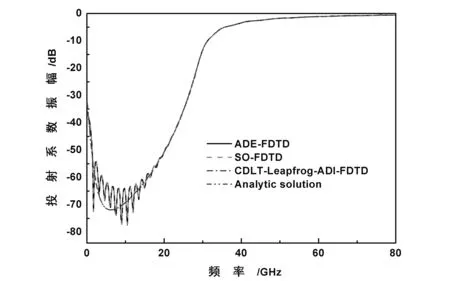
图3　三种FDTD方法计算6000步的透射系数振幅与解析解比较　

为了分析时间步长对于计算结果的影响，计算了系数CFLN取不同值时的等离子平板的反射系数和透射系数振幅，如图4所示。可知，随着CFLN的增大，即时间步长增大，反射系数振幅在频率较高处出现了微小的向较低频率方向偏移的趋势，但总体吻合较好，这是因为时间步长增大，频率越高数值色散也就越大，可根据具体问题精度的需要选择合适的时间步长。透射系数振幅吻合较好，可见，时间步长的增大对于透射系数的影响较小。因此，本文方法是一种精度和计算效率均较高的等离子体计算方法。

4　结论

(a)反射系数振幅　

(b) 透射系数振幅图4　系数CFLN取不同值时的反射系数和透射系数振幅　

本文首次采用CDLT方法将Leapfrog-ADI-FDTD方法推广到等离子体电磁特性的计算中，该方法不仅具有无条件稳定的特性，而且与传统FDTD方法一样，可在整时间步和空间步交替计算电场和磁场，提高了计算效率。本文提出的算法不论在精度上还是在效率上都高于普通的ADE-FDTD方法和SO-FDTD方法，并且易于推广到普通媒质和有耗色散媒质的计算中，具有良好的普适性。

[1]莫锦军，刘少斌，袁乃昌.等离子体覆盖导体柱宽带散射特性分析[J].微波学报，2003，19(1)：20-24.

[2]VidmarRJ.Ontheuseofatmosphericpressureplasmaaselectromagneticreflectorsandabsorbers[J].IEEETransonPlasmaSci，1990，18(4)：733-741.

[3]LaroussiM，RothJR.Numericalcalculationofthereflection，absorption，andtransmissionofmicrowavesbyanonuniformplasmaslab[J].IEEETransonPlasmaSci，1993，21(4)：366-372.

[4]刘少斌，张光甫，袁乃昌.等离子体覆盖立方散射体目标雷达散射截面的时域有限差分法分析[J].物理学报，2004，53(8)：2633-2637.

[5]韦笑，彭世鏐，殷红成，印国泰.基于平衡流场的再入飞行器电磁散射特性分析[J].系统工程与电子技术，2011，33(3)：506-510.

[6]NiekisehLJ，FrallkePM.Finite-differencetime-domainsolutionofMaxwell’sequationsforthedispersiveionosphere[J].IEEEAntennasPropagatMag，1992，34(1)：33-39.

[7]葛德彪，吴跃丽，朱湘琴.等离子体散射FDTD分析的移位算子方法[J].电波科学学报，2003，18(4)：359-362.

[8]杨利霞，王祎君，王刚.基于拉氏变换原理的三维磁化等离子体电磁散射FDTD分析[J].电子学报，2009，37(12)：2711-2715.

[9]GarciaSG，RubioRG，BretonesAR，etal.ExtensionoftheADI-FDTDmethodtoDebyemedia[J].IEEETransactionsonAntennasandPropagation，2003，51(11)：3183-3186.

[10]PeredaJA，GonzalezO，GrandeA，etal.Analternating-directionimplicitFDTDmodelingofdispersivemediawithoutconstituderelationsplitting[J].IEEEMicrowaveandWirelessComponentsLetters，2008，18(11)：719-721.

[11]汤炜，胡茂兵.辅助方程-双向隐式差分法的电磁散射研究[J].电波科学学报，2011，26(5)：904-909.

[12]殷雄，赵振维，张厚，等.等离子体散射分析的改进型交替隐式时域方法[J].电波科学学报，2013，28(2)：354-360.

[13]CookeSJ，BottonM，AntonsenT，etal.ALeapfrogformulationofthe3-DADI-FDTDalgorithm[J].InternationalJournalofNumericalModelling：ElectronicNetworks，DevicesandFilds，2009，22(2)：187-200.

[14]YangSC，ChenZ，YuY，etal.Anunconditionallystableone-steparbitrary-orderleapfrogADI-FDTDmethodanditsnumericalproperties[J].IEEETransAntennasPropag，2012，60(4)：1995-2003.

[15]TanEL.Fundamentalschemesforefficientunconditionallystableimplicitfinite-differencetime-domainmethods[J].IEEETransAntennasPropag，2008，56(1)：170-177.

(责任编辑：王谦)

CDLT-Leapfrog-ADI-FDTDMethodinPlasma

CHENGDan1，2，YINHong-cheng3，WEIxiao3，ZHENGHong-xing2

(1.InformationEngineeringSchool，CommunicationUniversityofChina，Beijing100024，China； 2.InstituteofAntennaandMicrowaveTechniques，TianjinUniversityofTechnologyandEducation，Tianjin300222，China； 3.ScienceandTechnologyonElectromagneticScatteringLaboratory，Beijing100854，China)

Thenontime-step-splittingleapfrogalternating-direction-implicitfinite-difference-time-domain(Leapfrog-ADI-FDTD)methodisextendedtoplasmabasedontheCDLT(CurrentDensityLaplaceTransform)method.TheLeapfrog-ADI-FDTDformulationsforisotropicplasmaarederived.Inordertodemonstratetheeffectivenessofthisapproach，thereflectionandtransmissionratioofplasmaplatearecalculated.ThenumericalresultsshowthattheproposedunconditionallystablemethodimprovesaccuracyandefficiencyovertheconventionalFDTDmethods.

plasma；leapfrog；Finite-DifferenceTime-DomainMethod；ADI

2016-03-18

国家自然科学基金面上项目(61371043)；天津应用基础与前沿技术研究计划青年项目(14JCQNJC01100)；天津市优秀青年教师资助计划项目(RC14-39)

成丹(1981-)，女(汉族)，黑龙江饶河人，中国传媒大学博士研究生.E-mail：chengdan_tute@126.com

TM154.3

A

1673-4793(2016)03-0033-05