国家授时中心昊平站40 m口径射电天线相位中心参考点坐标的精密测定

田　镇　杨志强 　石　震　党永超　张　喆

1　长安大学地质工程与测绘学院,西安市雁塔路南段126号，710064 2　国家测绘地理信息局第一地理信息制图院,西安市友谊东路334号，710054 3　中国科学院国家授时中心，陕西市书院东路3号，710600



国家授时中心昊平站40 m口径射电天线相位中心参考点坐标的精密测定

田镇1杨志强1石震1党永超2张喆3

1长安大学地质工程与测绘学院,西安市雁塔路南段126号，710064 2国家测绘地理信息局第一地理信息制图院,西安市友谊东路334号，710054 3中国科学院国家授时中心，陕西市书院东路3号，710600

给出国家授时中心昊平站40 m口径射电天线相位中心参考点坐标的测量技术方案，包括GPS控制网布设、观测及解算，天线旋转中心的测定与曲线拟合以及天线旋转中心坐标到参考点坐标的转化等。精度分析表明，所得的天线相位中心参考点在CGCS2000坐标系下的点位精度优于8 mm。

射电天线；旋转中心；相位中心参考点；曲线拟合；坐标转换

中国科学院国家授时中心昊平观测站位于陕西省洛南县保安镇，距离西安市150 km。40 m口径天线结合信号接收、信号采集和数据存储等设备，共同组成了空间信号质量监测评估系统。该系统主要用于跟踪和接收GNSS卫星下行信号，实现GNSS卫星信号的高精度观测和分析。精确的天线相位中心坐标在系统运行及维护过程中非常重要，而求取相位中心的三维坐标，必须首先以较高的精度测定天线相位中心参考点(以下简称参考点)的坐标。

1　天线参考点坐标测量方案

射电天线的参考点位于反射体之上，其空间位置会随着天线方位角和俯仰角的变化而变化[1]，难以直接采用大地测量的方法标定其坐标。但在天线设计之初，参考点与旋转中心的几何关系已经确定，且天线安装之后这一几何关系基本不会发生变化。因此，可以先测定旋转中心的空间坐标，再通过坐标转换求得参考点坐标。

本文选定天线支臂水平面与竖直旋转轴的交点作为旋转中心，如图1所示。首先在天线四周布置GPS控制点，并进行长时间观测，求出控制点坐标；然后在天线支臂上、旋转中心附近设置标志点，当天线水平旋转一周时，标志点的轨迹将形成一个圆形。在控制点上架设全站仪，采用极坐标法测量得到标志点的平面坐标，再由标志点的平面坐标进行圆曲线拟合[2]，求得圆心坐标，即为旋转中心的平面坐标。由于标志点与旋转中心处于同一平面，且天线水平旋转，因此两者的高程值相等，在控制点上进行三角高程测量即可得到旋转中心的高程。根据得到的旋转中心的三维位置，再通过坐标转换求得参考点的坐标。整个测量过程分为3步：1)GPS控制网布设、观测及解算；2)天线旋转中心的测定与坐标拟合；3)旋转中心坐标到参考点坐标的转化。

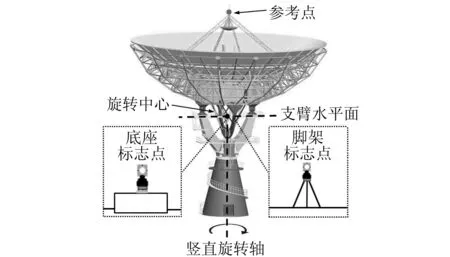
图1　天线旋转中心及标志点示意图Fig.1　The sketch of telescope’s rotation center and mark points

天线旋转中心的平面坐标由圆上标志点的坐标进行曲线拟合得到，其精度可能受圆半径的大小、点的位置分布和个数等的影响。因此，在测量工作之前有必要对上述因素的影响进行模拟分析。

假设由极坐标测量造成的圆上的标志点点位误差为5 mm，则生成一组均值为0、方差为0.0052、符合正态分布的随机变量X～N(0，0.0052)来模拟这一误差。再将一组分布于已知圆上的散点坐标与随机变量X叠加，用以模拟标志点的平面坐标值。由上述的坐标模拟值对圆曲线进行拟合，得到拟合圆的圆心坐标，其与已知的圆心坐标差值为ε，ε值的大小代表了模拟效果的好坏。为使得ε具有统计学效应，随机生成100组坐标模拟值，将由这100组坐标模拟值得到的ε作为母体，每个ε作为样本，分析在不同影响因素下ε的分布情况。

1.1圆半径大小对拟合精度的影响

分别使圆的半径为0.1 m、1 m、5 m、10 m、100 m，且都以均匀分布在圆上的8个模拟测点进行圆曲线拟合。重复100次实验，得到ε的平均值和标准差，见表1。

表1　不同圆半径条件下的ε统计值

由表1可知，当拟合点个数和分布不变，仅圆的半径发生变化时，ε的平均值和标准差几乎不变。由此可知，圆半径的大小对圆曲线拟合精度的影响很小。但考虑到天线整体受风、热及重力形变等影响，一般天线面板边缘的标志点测定精度弱于靠近天线旋转中心标志点的测定精度。因此，针对射电天线的特殊性，一般使圆的半径尽可能小。

1.2测点数量对拟合精度的影响

固定拟合圆的半径为0.1 m，分别采用个数为4、8、16、32、64，且均匀分布在圆上的模拟测点进行圆曲线拟合。同样重复100次实验，得到ε的统计值，见表2。

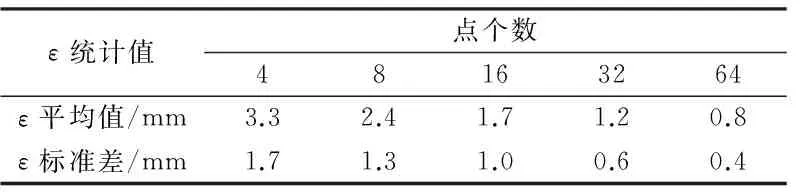
表2　不同测点个数条件下的ε统计值

由表2可知，在测点均匀分布且圆半径不变的情况下，随着测点个数的增多，ε的平均值和标准差均减小。由此可知，点个数越多，圆曲线的拟合精度越高，拟合得到的圆心坐标与真实值的偏差越小。

1.3测点分布对拟合精度的影响

固定拟合圆的半径为0.1 m，点个数为8，而这8个点分别分布于整个、3/4、1/2、1/4圆弧上。用上述点进行圆曲线拟合，再重复100次实验，得到ε的统计值见表3。

表3　不同点位分布下的ε统计值

由表3可知，在圆半径不变、测点个数一致的条件下，点位分布越均匀，ε的平均值和标准差越小。当所有点都分布在1/4圆弧上时，圆心的点位偏差甚至达到10.5±6.9 mm，几乎为测点点位误差的2～3倍。可见，点位的分布状况与最终的拟合结果关系较大。

2　GPS控制网施测及数据处理

2.1GPS观测基本情况

在天线周围建立4个相互通视的混凝土基墩，并设置强制对中作为GPS观测的控制点。控制网见图2。

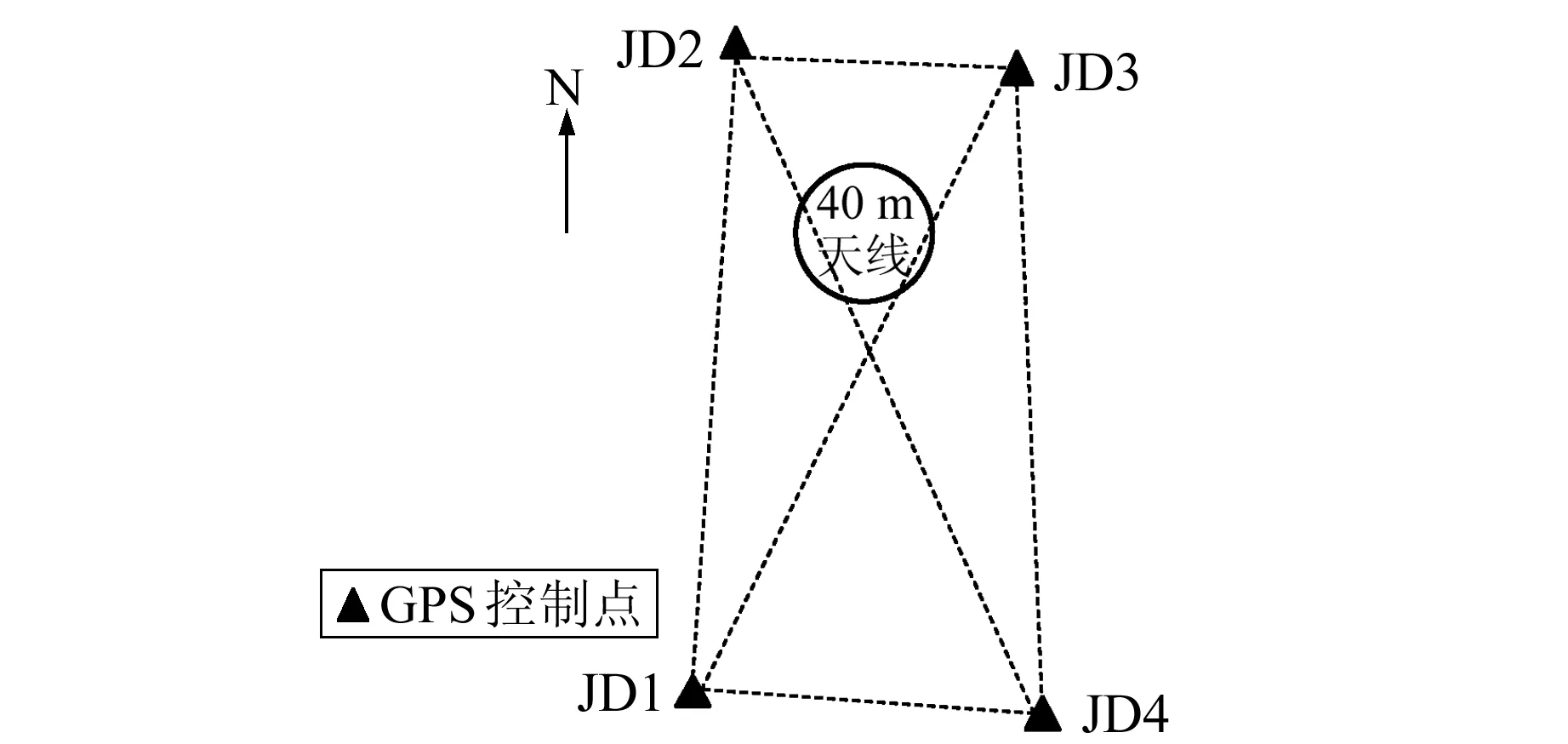
图2　GPS控制网示意图Fig.2　The sketch of GPS control network

GPS仪器采用Leica GS15。在4个控制点上同时且连续进行48 h以上的观测，接收机采样间隔30 s，天线高量取方式为到天线参考点的直高，便于数据处理时对天线参考点进行改化[3]。外业观测的卫星接收、PDOP等情况良好。

2.2GPS网数据处理

GPS网数据处理采用GAMIT/GLOBK软件。由于要求最终成果为CGCS2000坐标，因此将SNFX、SNLC、SNLX、SNSY、SNYX等5个连续运行的GPS站数据纳入GPS网一并处理[4]，同时加入海潮改正[5]。GPS网空间坐标精度情况见表4，最大点位误差为5.7 mm，平均点位误差为3.9 mm。

最后，将GPS控制点的空间直角坐标转换为大地坐标[6-7]，再以各控制点的平均经度作为中央子午线，平均大地高作为投影面高程，将控制点的大地坐标投影至高斯平面[8]，方便测量工作。

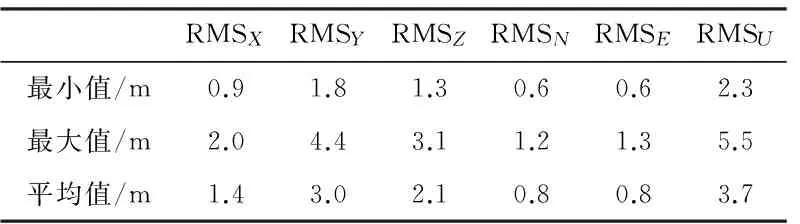
表4　GPS网坐标精度统计表

3　天线旋转中心测算与坐标拟合

因天线旋转中心附近空间狭窄，无法布设脚架，为此设计并加工可固定棱镜基座的底座设备(图3)。该底座带有螺丝的一面可装备棱镜，另一面直接用免钉胶固定在天线旋转轴附近的支臂上，形成底座标志点(图4(a))。同时，为了保证圆心坐标拟合的可靠性，在距旋转中心较远处架设三脚架，固定棱镜，形成脚架标志点(图4(b))。两标志点在天线上的大致位置见图1。

图3　底座Fig.3　The pedestal

图4　天线上设置的标志点Fig.4　The mark points in the telescope

采用Leica TC1800L型全站仪及其配套棱镜，距离测量精度为1 mm+2 ppm，角度测量精度为1″。在进行测量之前先对仪器进行检校，相同距离下不同棱镜的测距较差小于0.4 mm，说明仪器的系统误差较小，满足精度要求。

首先在JD3号控制点架设全站仪，JD4号控制点放置棱镜作为后视。天线绕竖直轴每旋转15°，全站仪分别照准底座和脚架标志点，观测水平角、斜距和天顶距，进行两测回。当天线旋转一周(360°)之后，再将全站仪搬至JD2、JD1号控制点，其余保持不动，照准标志点，分别重复上述步骤。最后可观测到31个底座标志点，但由于脚架标志点的部分角度被遮挡，只观测到17个脚架标志点。

以上各标志点根据观测得到的水平角、斜距和天顶距采用极坐标法计算得到其平面坐标，采用三角高程法求得其高程值。计算得到的坐标结果限于篇幅，在此省略。

上述标志点的平面坐标经圆曲线拟合可得其圆心坐标(图5)。其中底座测点较接近旋转中心，个数较多且分布较均匀；而脚架测点距旋转中心较远，且因部分角度遮挡，个数有限，集中分布在3/4的圆弧上。因此，将底座标志点的拟合值作为旋转中心的坐标结果，将脚架标志点的拟合值作为检核。经计算，两者差值为1.5 mm，偏差较小，说明拟合结果可靠性较高。最后，将得到的旋转中心的平面坐标和高程值，按照之前的投影参数转化为CGCS2000国家坐标系下的空间直角坐标[9]。

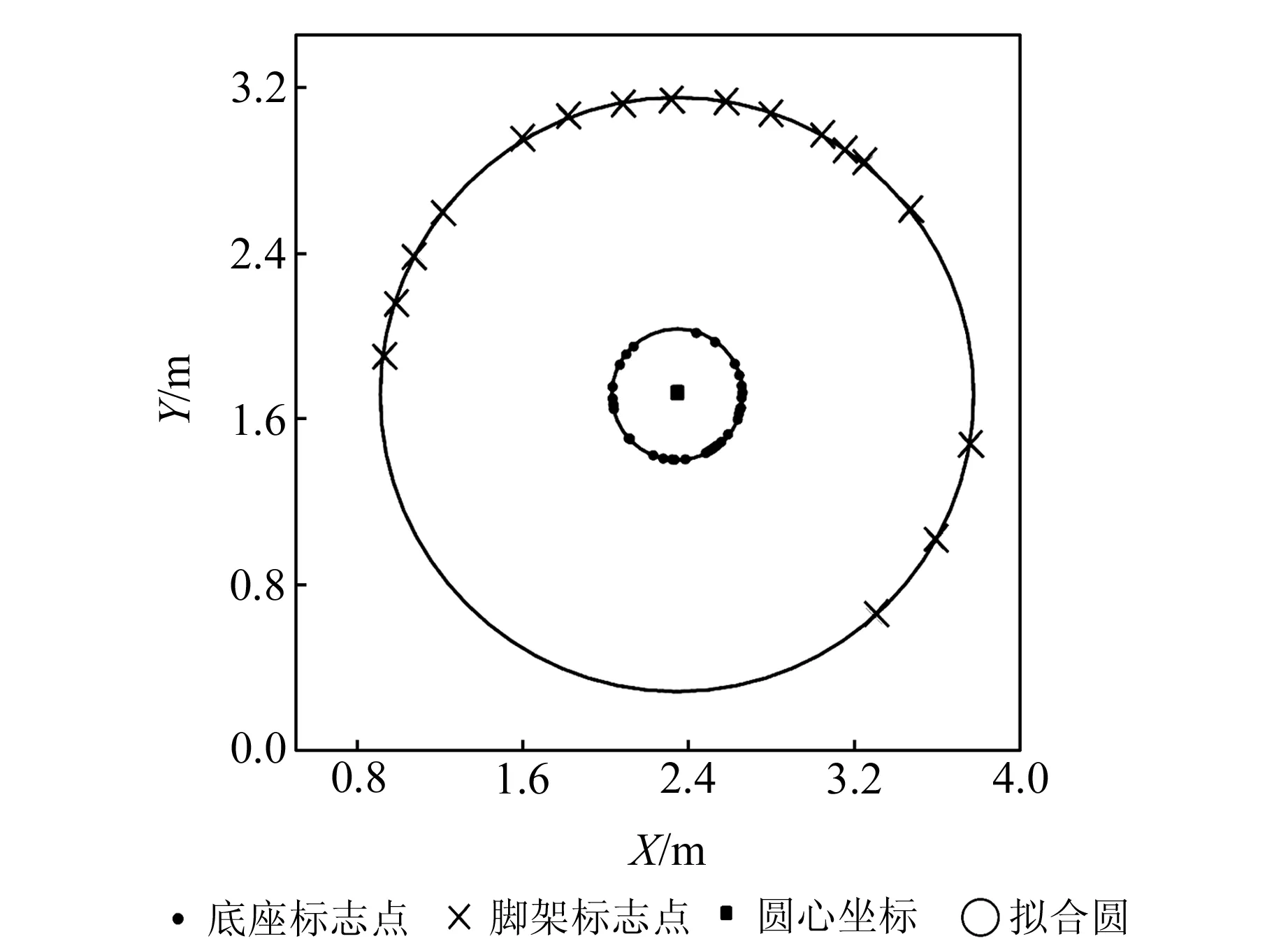
图5　标志点分布与圆心拟合Fig.5　The distribution of mark points and center of the circle fitting

4　天线旋转中心坐标到参考点坐标的转化

由于采用大地测量手段只能得到天线旋转中心的坐标，因此还需将天线旋转中心坐标归化到天线参考点。以旋转中心为原点，正东方向为x轴，正北方向为y轴，天顶方向为z轴，建立站心坐标系。天线的参考点与其俯仰角、方位角的位置关系可用如下函数关系表示：

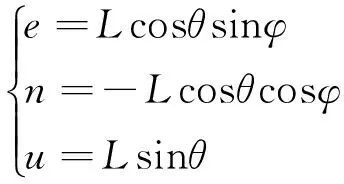
(1)

式中，(e,n,u)为参考点在站心坐标系下的坐标。当天线水平时，旋转中心与参考点的连线与竖直旋转轴重合，这一连线的距离即为L。

根据站心坐标到空间直角坐标的变换矩阵[10]，结合式(1)得到天线旋转中心至参考点的转换关系：

(2)

式中，(x0,y0,z0)、λ0和φ0分别为旋转中心的空间直角坐标、大地经度及大地纬度，(x,y,z)为参考点的空间直角坐标。

5　天线参考点精度分析

在上述坐标转化中，L值由天线生产单位给出，精度较高；同时，旋转中心坐标的误差对上述矩阵运算结果的影响也较小，所以旋转中心到参考点的转化误差可以忽略不计。因此，在测算过程中，天线参考点的误差来源有：GPS控制测量误差、圆曲线拟合误差(由极坐标测量的不准确造成)、三角高程测量误差以及参考点不稳定所带来的误差。

1)极坐标法测量点位误差Mp的公式为[11]：

(3)

式中，mβ为水平角测量误差，D为控制点到天线标志点的平距，mD为测距中误差，ρ≈206 265。

由于D≤80 m，而水平角观测两测回，结合仪器精度可知Mp≤1.1 mm。由此，设定标志点的点位误差为1.1 mm，个数为31，点位分布如图5。采用上述仿真模拟的方法得到拟合圆心坐标的点位偏差ε为0.3±0.1 mm，取其最大值0.4 mm作为圆曲线的拟合误差Mc。

2)近距离三角高程测量误差Mh的公式为[12]：

(4)

式中，α为竖角，mα为竖直角测量误差，mi、mv为仪器高和目标高量取误差。

由于|α|≤20°，而仪器高和目标高采用钢尺在不同方向量取多次取平均值，其量取误差可忽略不计。竖角观测两测回，结合仪器精度可知Mh≤0.5 mm。

3)对于大口径天线，其参考点因温度、风力等的影响，1 d中位置变化可达3～5 mm，取其最大值5 mm作为参考点不稳定所造成的误差M0。

由于上述误差相互独立，天线参考点的点位误差等于各独立误差值平方和的平方根[13]:

(5)

式中，Mg为GPS控制点的误差，取其最大值5.7 mm。再将其余误差值代入式(5)，得Mtotal≤7.7 mm，即天线参考点在CGCS2000坐标系下的坐标精度优于8 mm(小于限差2 cm)。而因为Mc、Mh都较小，所以除M0外，GPS控制点误差是旋转中心坐标的主要误差源。

6　结　语

对于平面上的旋转体，其运动轨迹所形成的圆的半径大小对最终的圆心坐标拟合精度基本没有影响。但由于天线体受风、热及重力形变等影响，位于天线面板边缘的标志点测定精度会弱于靠近旋转中心的标志点，因此，在其旋转中心的测量过程中，一般使得圆半径尽可能小。而轨迹点个数越多，分布越均匀，圆心的拟合精度越高。其中轨迹点分布的影响尤其显著，因而在测量过程中应尽可能使得测点均匀分布。

在采用本文方案且仪器精度较高、测点个数较多、分布较好的情况下，GPS控制点误差是除天线不稳定因素外的主要误差源，而天线不稳定误差属于不可控误差。因此，减小GPS控制测量所产生的误差是精确测定天线相位中心参考点坐标的前提。

[1]马下平,沈云中,王解先,等.卫星激光测距与甚长基线干涉测量的天线旋转中心的直接解法[J].测绘学报,2014，43(3):257-262(Ma Xiaping, Shen Yunzhong, Wang Jiexian, et al. Direct Solution of SLR and VLBI Antenna Rotation Center[J]. Acta Geodaetica et Cartographica Sinica,2014,43(3):257-262)

[2]刘光明,马金辉,唐颖哲. VLBI归心测量中的空间拟合[J]. 测绘通报, 2011(10): 11-13(Liu Guangming,Ma Jinhui,Tang Yingzhe. Fit Method in Determination of Space Coordinate Differences of VLBI Sites[J]. Bulletin of Surveying and Mapping, 2011(10): 11-13)

[3]郭际明,史俊波,汪伟. 天线参考点偏移和变化对高精度GPS数据处理的影响[J]. 武汉大学学报:信息科学版,2007,32(12):1 143-1 146(Guo Jiming, Shi Junbo, Wang Wei. Impact of Antenna Phase Center Offset and Variation for High Precision GPS Data Processing[J]. Geomatics and Information Science of Wuhan University,2007,32(12):1 143-1 146)

[4]陈俊勇. 中国现代大地基准——中国大地坐标系统2000(CGCS 2000)及其框架[J]. 测绘学报,2008,37(3):269-271(Chen Junyong. Chinese Modern Geodetic Datum--Chinese Geodetic Coordinate System 2000 (CGCS 2000)and Its Frame[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(3):269-271)

[5]郑祎,伍吉仓,王解先,等. GPS精密定位中的海潮位移改正[J]. 武汉大学学报：信息科学版, 2003, 28(4): 405-408(Zheng Yi, Wu Jicang, Wang Jiexian, et al. Ocean Tidal Displacement Corrections in GPS Precision Positioning[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 405-408)

[6]史海锋,张卫斌. 空间直角坐标与大地坐标转换算法研究[J]. 大地测量与地球动力学, 2012, 32(5): 78-81(Shi Haifeng, Zhang Weibin. Study on Transformation from Cartesian to Geodetic Coordinates [J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 78-81)

[7]Vermeille H .Computing Geodetic Coordinates from Geocentric Coordinates[J].Journal of Geodesy,2004 , 78(1):94-95

[8]邓兴升,汤仲安,花向红,等. 椭球变换后的高斯投影正反算算法[J]. 大地测量与地球动力学,2010,30(2):49-52(Deng Xingsheng, Tang Zhongan, Hua Xianghong, et al. Gauss-Kruger Projection Forward and Reverse Calculation after Ellipsoid Transform [J]. Journal of Geodesy and Geodynamics, 2010,30(2):49-52)

[9]过家春,赵秀侠,吴艳兰. 空间直角坐标与大地坐标转换的拉格朗日反演方法[J]. 测绘学报,2014,43(10):998-1 004(Guo Jiachun, Zhao Xiuxia, Wu Yanlan, et al. Transformation from Cartesian to Geodetic Coordinates Using Lagrange Inversion Theorem[J]. Acta Geodaetica et Cartographica Sinica, 2014,43(10):998-1 004)

[10]黄立人,高砚龙,任立生. 关于NEU(ENU)坐标系统[J]. 大地测量与地球动力学, 2006,26(1): 97-99(Huang Liren, Gao Yanlong, Ren Lisheng. OnNEU(ENU) Coordinate System[J]. Journal of Geodesy and Geodynamics, 2006,26(1): 97-99)

[11]何诚,巩垠熙,冯仲科,等. 超站仪极坐标法的运用及其探讨[J]. 测绘通报,2011(2):26-28(He Cheng, Gong Yinxi, Feng Zhongke, et al. Application and Study of Super Total Station’s Polar Coordinates Measurements[J]. Bulletin of Surveying and Mapping,2011(2):26-28)

[12]张正禄,邓勇,罗长林,等. 精密三角高程代替一等水准测量的研究[J]. 武汉大学学报:信息科学版,2006,31(1):5-8(Zhang Zhenglu, Deng Yong, Luo Changlin, et al. Research on Precise Triangulated Height Surveying in Place of First Order Leveling [J]. Geomatics and Information Science of Wuhan University,2006,31(1):5-8)

[13]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉:武汉大学出版社, 2009(Survey Adjustment Discipline Groups, School of Geodesy and Geomatics, Wuhan University. Error Theory and Basis of Surveying Adjustment[M]. Wuhan:Wuhan University Press,2009)

About the first author:TIAN Zhen,PhD candidate, majors in survey data processing theory and method,E-mail：tianzhen_vip@126.com.

Precise Measurement of 40 m Caliber Radio Telescope Phase Center’s Reference Point Coordinates at the Haoping Station of National Time Service Center

TIANZhen1YANGZhiqiang1SHIZhen1DANGYongchao2ZHANGZhe3

1College of Geology Engineering and Geomatics, Chang’an University,126 South-Yanta Road, Xi’an 710064,China 2First GIS Mapping Institution, NASMG, 334 East-Youyi Road,Xi’an 710054,China 3National Time Service Center, CAS, 3 East-Shuyuan Road,Xi’an 710600,China

The 40 m caliber radio telescope, at the Haoping station of the National Time Service Center, is crucial to satellite monitoring and maintenance work, but there is limited research on how to accurately measure the phase center reference point coordinates. Aiming at this problem, this article introduces the measurement solution of phase center reference point coordinates, including GPS control net setting, observation and data processing, the measurement of the rotation center’s coordinate and curve fitting, and the coordinate transformation of rotation center to reference point. The results of the precision analysis show that the accuracy of reference points is better than 8 mm in the CGCS2000 coordinate system.

radio telescope; rotation center; phase center’s reference point; curve fitting; coordinate transformation

National Natural Science Foundation of China,No.41504001;Fundamental Research Funds for the Central Universities,No.310826151047.

2015-09-17

田镇，博士生，主要从事测量数据处理理论与方法研究，E-mail：tianzhen_vip@126.com。

10.14075/j.jgg.2016.10.012

1671-5942(2016)010-0897-05

P226

A

项目来源：国家自然科学基金(41504001)；中央高校基本科研业务费(310826151047)。