基于三维Taylor多项式建立局域海洋地磁场模型

种　洋　柴洪洲

1　信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2　地理信息工程国家重点实验室，西安市雁塔路中段1号，710054 3　海军工程大学导航工程系，武汉市解放大道717号，430033



基于三维Taylor多项式建立局域海洋地磁场模型

种洋1,2,3柴洪洲1

1信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2地理信息工程国家重点实验室，西安市雁塔路中段1号，710054 3海军工程大学导航工程系，武汉市解放大道717号，430033

在海洋磁力测量中,波浪和风等外界因素的变化会对磁力测量数据在垂直空间上产生影响，而二维Taylor多项式在建立局域海洋地磁场模型时没有考虑高度变化对模型的影响。针对这一问题，提出使用三维Taylor多项式完全展开法来构建局域海洋地磁场模型，通过模拟某海域水下球体磁场，仿真船载磁力测量数据，分析两种模型截断阶数的选择、完全与不完全展开的区别和模型边界效应等问题。实验表明，在顾及高度变化的情况下，三维Taylor多项式模型能更详细地反映海洋磁力异常的分布情况，且较好地改善了边界效应。

局域海洋地磁场模型；三维Taylor多项式；截断阶数；边界效应

海洋磁力测量是采用船拖着拖鱼进行测量。由于风浪、船速、潮汐等影响，拖鱼在整个测量过程中不规则上下摆动。同时，在进行大面积海洋磁力测量时，是采用多艘船并列前行同时测量，由于船的各项参数不同以及缆绳长度不一等，拖鱼入水的深度也不同，导致整个观测面是一个不规则的起伏曲面。目前国内外处理海洋磁力测量数据时所用的磁力异常计算公式为[1-3]：

(1)

式中，ΔT为海洋地磁异常值,T为地磁场总测量值，Td为地磁日变改正值，Ts为船磁改正值，To为地磁正常值。

海洋磁力测量数据在通过式(1)进行各项改正时，只进行了平面上的变换，而忽略了观测面在垂直方向的变化，所以处理后的测量数据面仍然是曲面。

局域地磁场模型的构建主要包括矩谐分析法、Taylor多项式法和球冠谐和分析法等[4-6]，其中Taylor多项式法是至今仍然被广泛采用的方法之一。简单地讲，Taylor多项式法就是将地磁要素用多项式形式表示成为平面坐标或者经纬度的函数，由求解得到的模型系数来表示该区域的地磁场变化情况[7]。该方法建模速度快，可高效地计算出地磁场各要素。但Taylor多项式模型是在二维平面内描述地磁场在地球表面的分布情况，而没有顾及到高度变化对模型所产生的影响[8-9]。本文在传统Taylor多项式的基础上，顾及拖鱼入水深度不同对船载磁力测量中垂直方向的影响，提出使用三维Taylor多项式完全展开法来构建局域海洋地磁场模型，通过模拟某海域水下球体磁场，仿真船载磁力测量数据，分析比较两种模型截断阶数的选择、完全与不完全展开的区别和模型边界效应等，得到了一些有益的结论。

1　三维Taylor多项式模型

Taylor多项式法构建局域地磁场模型的基本思想是将地磁要素表示为地理位置的函数，传统的二维Taylor多项式模型是对某一地磁要素进行部分三角阵展开。地理位置可以用(x,y)表示，二维Taylor多项式可以表示为[10]:

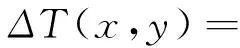
(2)

式中，ΔT为磁力异常；Aij为多项式模型的系数，由最小二乘法确定；N为多项式模型的截断阶数；x、y为坐标值；(x0,y0)为模型展开原点的坐标值，一般选择建模区域的中心位置为展开点；i-j和j为平面坐标的展开阶数。由于是部分三角阵展开，本文中统称为二维Taylor多项式不完全展开。

进一步可得二维Taylor多项式完全展开形式为：

(3)

相比式(2)，式(3)平面坐标展开阶数为j和i，系数矩阵Aij为N×N的方阵。

考虑到高度变化对模型的影响，应采用三维Taylor多项式完全展开式建立海洋地磁场模型，其表达式为：

(4)

综上所述，可将顾及垂直方向影响的船载磁力测量磁测数据处理计算步骤总结如下。

1)在测区中心选取参考点O并确定基准参考平面高度，构建相应的局部空间直角坐标系，并进行坐标转换；

2)通过对数据的分析和测试，选择合适的截断阶数；

3)按照上述Taylor多项式方法构建法方程，利用最小二乘方法求得的系数表示出整个观测区域内的模型计算值，并对新模型进行分析评定。

为检验上述方法的建模效果，使用球体磁场仿真的船载磁测数据进行实验。

2　局域海洋地磁场数据仿真方法

模拟某海域磁场测定的实际磁力测量，选定一定的参数，仿真一个球体磁场作为经过式(1)中各项改正后的磁场。球体磁场的计算公式为[1]：

(2x2-y2-(z-R)2)cos2Icos2A′+

(2y2-x2-(z-R)2)cos2Isin2A′-

3x(z-R)sin2IcosA′+3xycos2Isin2A′-

3y(z-R)sin2IsinA′)

(5)

式中，μ0为真空磁导率；m为磁矩,m=MV,M为磁化强度,V为球体体积；R为球体中心埋深；(x,y)为空间一点的平面坐标；I为磁化倾角；A′为磁化偏角。

本文采用的球体模型参数如表1所示。

在仿真时，选取仿真区域大小为5 000m×5 000m，区域中主测线100条，检查线6条，共100×100个观测点，点距和线距为50m；球体位于区域中心，球心埋深为60m，且以区域海平面中心为原点，x轴与测线方向平行，y轴与基线方向平行，z轴垂直xoy面向下建立坐标系。

表1　仿真球体参数

在式(5)中取z=0代入计算,可得一组各观测点的磁力异常值。取z=0的平面即xoy面作为基准平面，则该组磁力异常值即为各测点在基准面上的磁力异常值。为了方便说明问题，此处选取仿真区域中x、y均为2 200～2 700 m范围的数据处理结果。计算结果如图1所示。

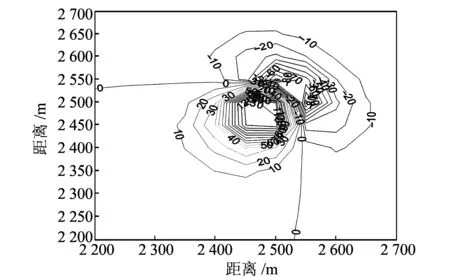
图1　基准平面上的磁异常等值线Fig.1　Magnetic anomalies contour of reference plane

图1表示的是磁性球体在基准平面上的磁异常分布等值线图，等值线单位为nT。可以看出，磁性球体在基准平面上的磁异常分布均匀，具有明显的正异常和负异常，左下方的等值线代表正异常值，右上方的等值线代表负异常值，正负异常在±100 nT范围内波动。

而实际海洋磁力测量中，拖鱼的运动状态是上下起伏的，其相对于基准面存在一个高差Δz，当观测点在基准面上时z>0，当观测点在基准面下时z<0。根据各测点拖鱼的起伏状态，取相应的z值代入式(5)，可得各测点的另一组磁力异常值，即为各测点在观测曲面上的磁力异常值。仿真出的观测曲面如图2所示。

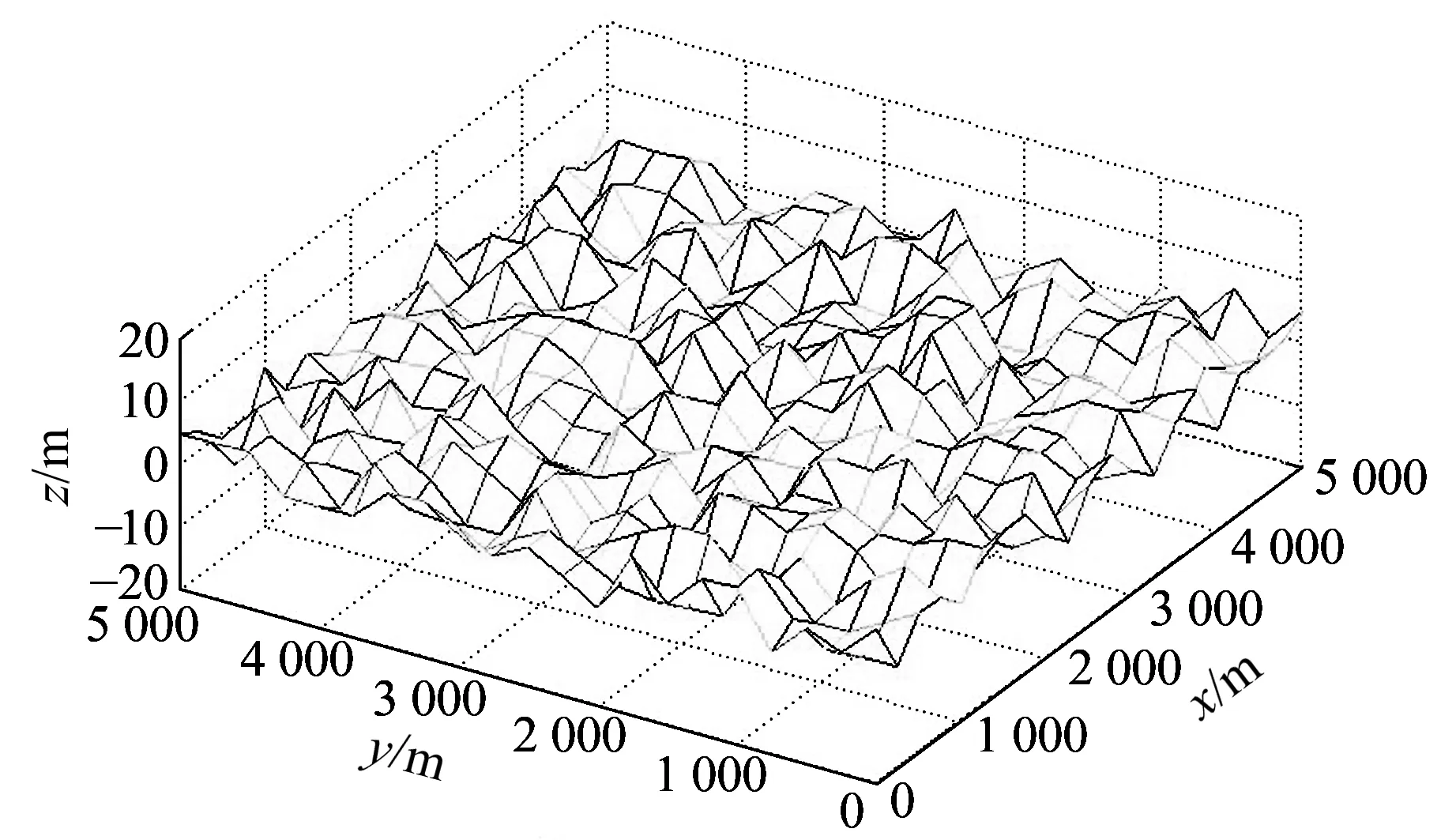
图2　观测曲面变化的立体图Fig.2　The three-dimensional variations of observation surface

图2中，(x,y)为观测点坐标，z为拖鱼在测量过程中相对于基准面的上下起伏变化量，其最大变化量为4.11 m。在得到了基准平面和仿真观测曲面上的磁力异常值后，通过作二者的等值线图对其进行对比分析，如图3所示。

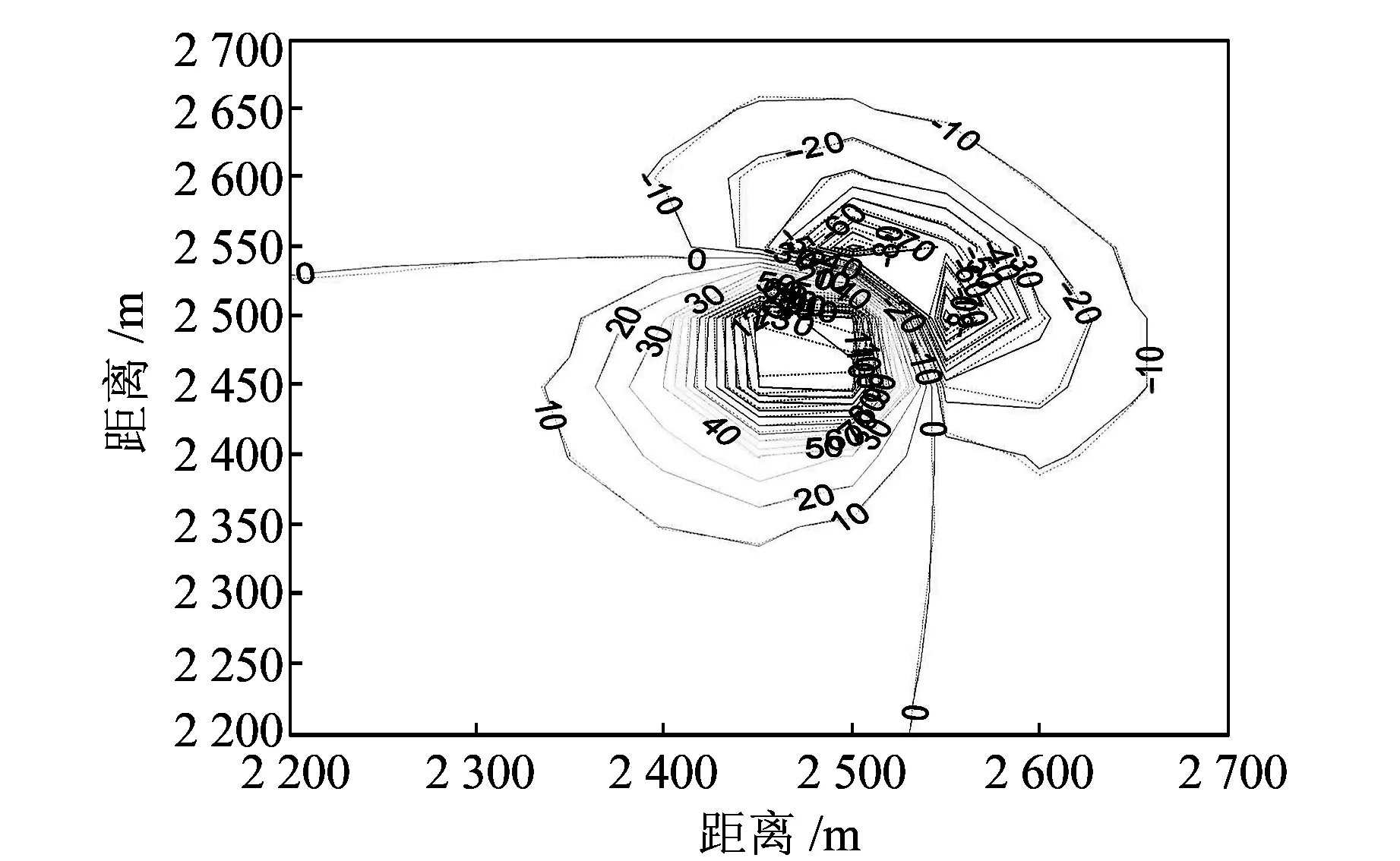
图3　基准平面和仿真观测曲面的磁异常等值线分布Fig.3　Distributions of magnetic anomalies contour between reference plane and simulation observation surface

图3中实线表示观测点在基准平面上的磁力异常值，虚线表示观测点在仿真观测曲面上的磁力异常值。可以看出，同一观测点在基准面上(z=0)和在仿真观测曲面上的磁力异常值是不一样的，且在磁力异常变化较剧烈的地方二者差距比较明显。这说明，如果不顾及海洋磁力测量中拖鱼在垂直方向上的波动变化，将会对最终的海洋地磁场建模结果产生一定的误差影响。因此，在实际的磁力测量中需要考虑垂直方向的变化。

3　截断阶数的选取

Taylor多项式法在构建局部地磁场模型时，选择合适的截断阶数是一项重要内容。截断阶数过低，则模型过于简单，损失了大部分有价值的信息，从而不能很好地表示地磁场的时空分布；截断阶数过高，会使模型结果的稳定性降低，同时会增加模型计算的复杂性，产生严重的边界效应。

选取截断阶数的方法通常有两种：一是通过区域地磁场模型的均方误差(RMS)应小于相应年代的国际地磁参考场(IGRF)的均方误差来选取；二是通过对不同截断阶数下模型结果的均方误差进行比较，当其值比较小且趋于稳定时，即可选为模型的截断阶数。均方误差的计算公式为：

(6)

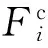
3.1二维Taylor多项式完全展开模型截断阶数的选取

当z=0时，利用基准面上观测点的磁力异常数据，通过二维Taylor多项式完全展开与不完全展开法构建模型，并分别计算不同截断阶数下两模型的均方误差，结果如图4所示。

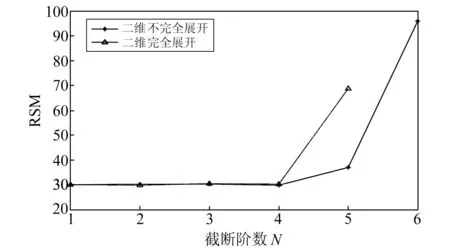
图4　二维Taylor多项式不完全与完全展开的磁力异常均方误差与截断阶数的关系Fig.4　The relationship between the mean square error and the truncation order of the magnetic anomalies under the classical and complete two-dimensional Taylor polynomial expansion

由图4可以看出，当N≤4时，两者相应的均方误差都随着N的变化而趋于平稳，且两者的精度大致相当，而完全展开模型在N=4时的精度与不完全展开模型在N=5时的精度相差不大；当N>4时，完全展开模型的均方误差随着N的变化而急剧增大。分析可知，当N≥4时完全展开模型结果的不稳定性显著增大，而不完全展开模型的截断阶数虽然可以取到N=5,但精度却没有得到实质性的提高，且加大了计算量。这表明，在同样没有高度变化的基础上，采用二维Taylor多项式完全展开法来构建模型要好一些。综合考虑均方误差的大小和模型的复杂性可知，二维Taylor多项式完全展开模型的截断阶数选N=4比较合适。

3.2三维Taylor多项式完全展开模型截断阶数的选取

当z方向上有高度变化时，利用仿真所得的曲面磁力异常数据，通过二维和三维Taylor多项式完全展开法分别构建模型，分别计算不同截断阶数下两种模型的均方误差，结果如图5所示。

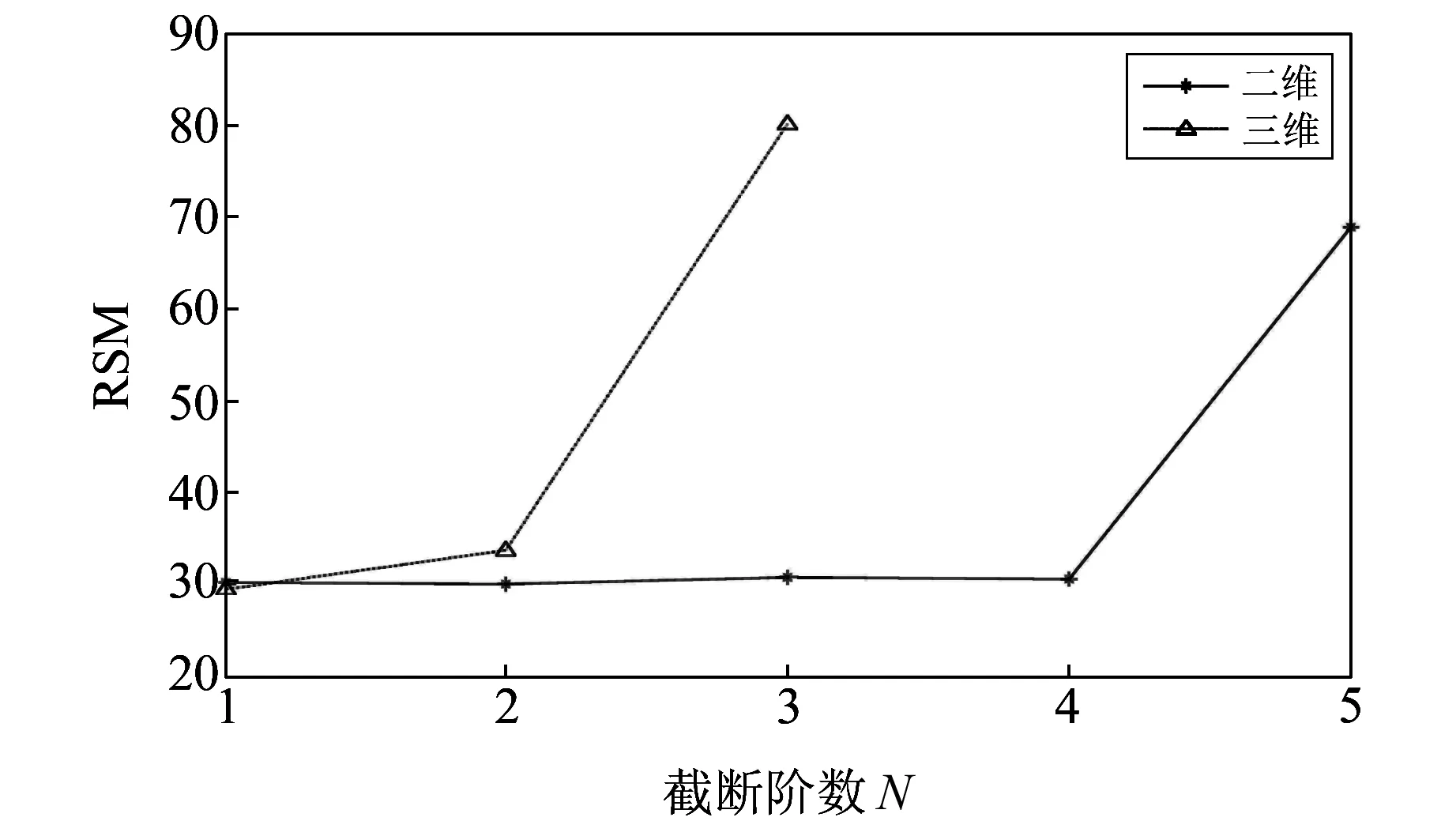
图5　二维与三维Taylor多项式完全展开的磁力异常的均方误差与截断阶数的关系Fig.5　The relationship between the mean square error and the truncation order of the magnetic anomalies under the complete two-dimensional and three-dimensional Taylor polynomial expansion

由图5可知，三维完全展开模型在N=1时就达到了二维完全展开模型在N=4时的精度，且精度更高；当N≥2时，三维完全展开模型的均方误差随着N的变化急剧增大，而二维完全展开模型的截断阶数则可以取到N=4，但精度却没有得到明显的改善。分析可知,当N>2时三维完全展开模型开始变得不稳定，而二维完全展开模型在N>4时才开始变得不稳定，这主要是因为三维完全展开模型直接考虑了高度变化的影响，其所展开的模型系数更多，模型更加符合实际情况。结果表明，在观测数据有高度变化时，利用三维Taylor多项式完全展开法来构建模型，截断阶数取N=1即可得到理想结果。

4　边界效应分析

在提高区域模型精度的过程中，由于区域边界处地磁测量点稀少，进而随着函数逼近，出现区域边界处的误差逐渐增大的现象，即所取海洋地磁场区域模型的边界部分会涉及到边界效应问题。本文通过比较二维和三维Taylor多项式完全展开模型，进一步分析该问题。比较结果如图6所示。

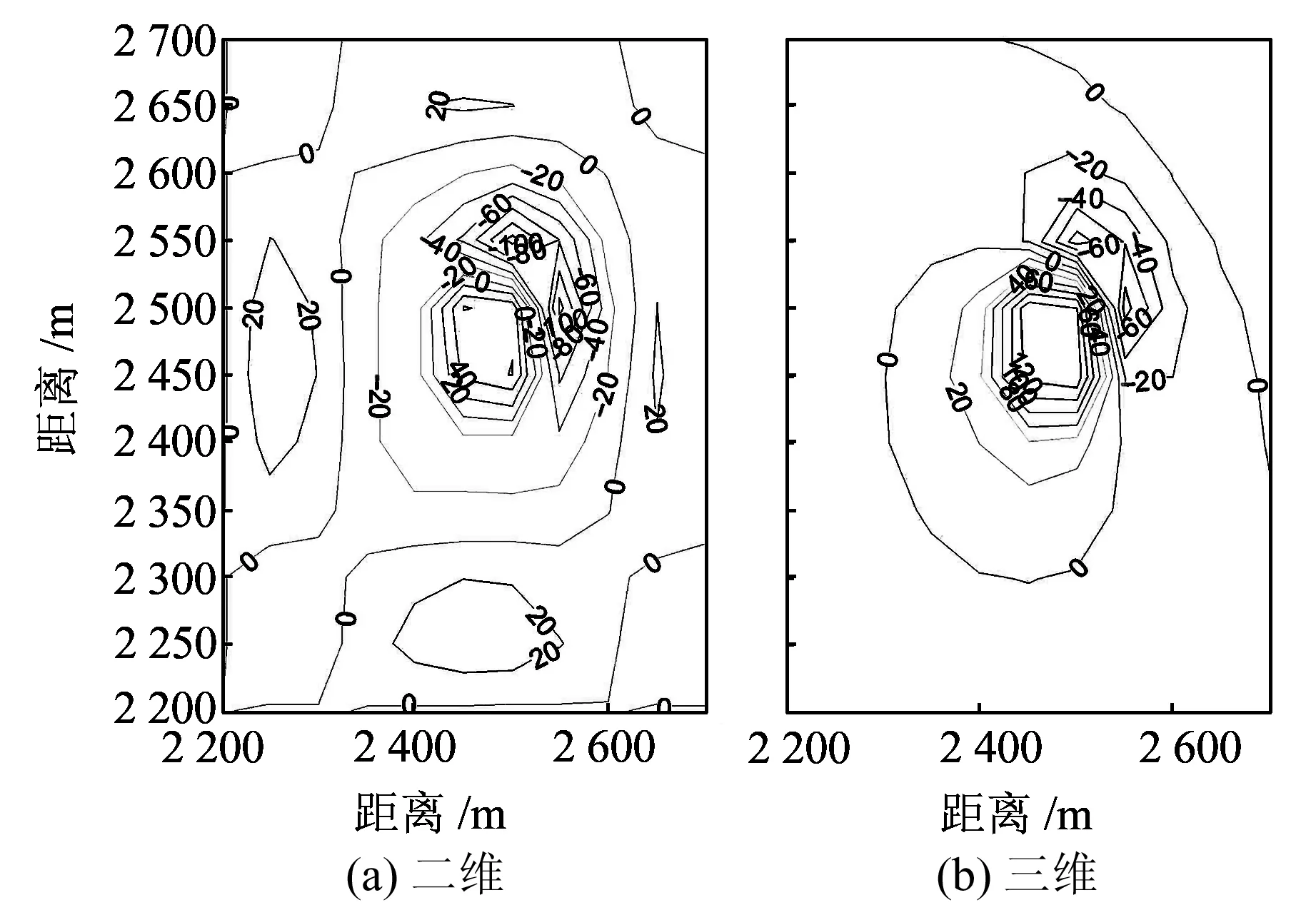
图6　二维与三维Taylor多项式完全展开的磁力异常边界效应比较Fig.6　The boundary effects of the magnetic anomalies under the comparison of the complete two-and three-dimensional Taylor polynomial expansion

由图6可知，与二维Taylor多项式相比，三维Taylor多项式在边界的畸变较小，且较为集中。因此，三维Taylor多项式能较好地改善边界效应。

5　结　语

通过对Taylor多项式完全展开与不完全展开的比较、二维Taylor多项式法与三维Taylor多项式法的截断阶数及边界效应的对比，分析可得下列结论：

1)海洋磁力测量中,波浪和风等外界因素变化的影响导致了拖鱼在垂直空间上产生不规则起伏。顾及高度的变化，通过三维Taylor多项式法对垂直空间进行改正，海洋磁力测量数据处理结果精度得到提高。若忽略垂直方向的变化，则会对后期局域地磁场建模精度产生一定的影响。

2)利用三维Taylor多项式法计算时要考虑到截断阶数的影响。阶数的选取需要顾及精度和可靠性两方面的影响。实验结果表明，利用三维Taylor多项式法在截断阶数较低(N=1)时的计算精度与二维Taylor多项式法在较高截断阶数(N=4)时的精度大致相当。

3)考虑到边界效应的影响，用三维Taylor多项式法得到的磁力异常更具有合理性，而不需要采用平滑因子的方法或者是增加IGRF边界点的方法来克服该问题。此外，在一些对实时性要求较高的领域，如高速弹道导航等[11-13]，由于三维Taylor多项式方法在精度上不亚于其他局域建模方法，且计算简单，故实时性比较好，可以得到比较好的应用。如果以后有了航磁数据[14]和卫星数据，可以使本方法的模型空间范围由深海拓展到更广的范围。

[1]于波, 翟国君, 刘雁春,等. 海洋磁力测量的垂直空间改正[J]. 大地测量与地球动力学, 2008, 1(1):123-126(Yu Bo, Zhai Guojun, Liu Yanchun, et al. Vertical Free-Air Correction in Marine Magnetics Survey[J]. Journal of Geodesy and Geodynamics, 2008, 1(1): 123-126)

[2]徐文耀. 地球电磁现象物理学[M]. 合肥：中国科学技术大学出版社, 2009(Xu Wenyao. Physics of Electromagnetic Phenomena of the Earth[M]. Hefei: University of Science and Technology of China Press, 2009)

[3]徐文耀. 地磁学[M]. 北京: 地震出版社, 2003(Xu Wenyao. Geomagnetism[M]. Beijing: Seismology Press, 2003)

[4]徐文耀, 朱岗崑. 我国及邻近地区地磁场的矩谐分析[J]. 地球物理学报, 1984, 27(6): 511-522(Xu Wenyao, Zhu Gangkun. A Study of the RHA for the Geomagnetic Field of China and Neighboring Region[J].Acta Geophysica Sinica, 1984, 27(6): 511-522)

[5]安振昌. 区域和全球地磁场模型[J]. 地球物理学进展,1995,10(3):63-73(An Zhenchang. Regional and Global Geomagnetic Field Models[J]. Progress in Geophysics, 1995, 10(3): 63-73)

[6]徐文耀, 区加明, 杜爱民. 地磁场全球建模和局域建模[J]. 地球物理学进展, 2011, 26(2)：398-415(Xu Wenyao, Ou Jiaming, Du Aimin. Geomagnetic Field Modeling for the Globe and a Limited Region[J]. Progress in Geophys, 2011, 26(2)：398-415)

[7]常宜峰.局域海洋地磁场模型及磁力异常数据探测方法研究[D].郑州:信息工程大学,2012(Chang Yifeng. Research on Local Marine Geomagnetic Field Model and Detecting of Geomagnetic Abnormal Data[D]. Zhengzhou: Information Engineering University, 2012)

[8]杨云涛,石志勇,关贞珍,等.一种改善区域地磁场模型边界效应的方法[J].地球物理学进展,2009,24(2): 468-474(Yang Yuntao, Shi Zhiyong, Guan Zhenzhen, et al. A Method of Improving Regional Geomagnetic Field Model Boundary Effect[J]. Progress in Geophysics, 2009,24(2): 468-474)

[9]乔玉坤,王仕成,张金生,等.泰勒多项式拟合法在区域地磁场建模中的应用研究[J].工程地球物理学报,2008,5(3):294-298(Qiao Yukun, Wang Shicheng, Zhang Jinsheng, et al. Research on Taylor Polynomial Fitting in Modeling of Regional Geomagnetic Field[J]. Chinese Journal of Engineering Geophysics,2008,5(3):294-298)

[10]安振昌, Rotanova N M. 东亚地磁场模型的计算与分析[J]. 地球物理学报, 2002, 45(1):34-41(An Zhenchang, Rotanova N M. Calculations and Analyses of the Geomagnetic Field Models for East Asia[J]. Acta Geophysica Sinica, 2002, 45(1):34-41)

[11]李素敏，张万清．地磁场资源在匹配制导中的应用研究[J]. 制导与引信，2004，25(3)：19-21(Li Sumin, Zhang Wanqing. Study on the Application of Geomagnetic Field Contour in Matching Guidance[J]. Guidance & Fuze, 2004, 25(3): 19-21)

[12]彭富清, 霍立业. 海洋地球物理导航[J]. 地球物理学进展，2007，22(3)：759-764(Peng Fuqing，Huo Liye. Marine Geophysical Navigation[J]. Progress in Geophysics, 2007, 22(3): 759-764)

[13]徐文耀, 国连杰．空间电磁环境研究在军事上的运用[J]．地球物理学进展，2007，22(2)：335-344(Xu Wenyao, Guo Lianjie. Study of Space Electromagnetic Environment and its Application on Military Affairs[J]. Progress in Geophysics, 2007, 22(2)：335-344)

[14]熊盛青．我国航空重磁勘探技术现状与发展趋势[J]. 地球物理学进展, 2009, 24(1)：113-117(Xiong Shengqing. The Present Situation and Development of Airborne Gravity and Magnetic Survey Techniques in China[J]. Progress in Geophys, 2009, 24(1): 113-117)

About the first author:CHONG Yang, postgraduate, majors in geomagnetism aided navigation, E-mail: chongyang_geodesy@outlook.com.

Regional Marine Geomagnetic Field Model Reconstruction Based on Three-Dimensional Taylor Polynomial

CHONGYang1,2,3CHAIHongzhou1

1Institute of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China 2State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi’an 710054, China 3Department of Navigation, Naval University of Engineering, 717 Jiefang Road, Wuhan 430033, China

Wave and wind effect marine magnetic survey data in the vertical space. This is because the two-dimensional Taylor polynomial doesn’t include the influence of the change of height in establishing the regional marine geomagnetic field model. In order to solve this problem, a three-dimensional Taylor polynomial is put forward to construct the regional marine geomagnetic field model. By simulating a certain area of underwater sphere magnetic field and ship-borne magnetic survey data, this paper analyzes choosing the truncation order of the two models, the difference between the complete polynomial expansion and the classical expansion methods, and the boundary effect of the two methods. The results show that: the three-dimensional Taylor polynomial method can reflect the distribution of marine magnetic anomalies better and overcomes the boundary effects in considering the height changes.

regional marine geomagnetic field model; three-dimensional Taylor polynomial method; truncation order; boundary effect

National Natural Science Foundation of China, No. 41574010, 41274045, 41476087; Open Fund of State Key Laboratory of Geo-Information Engineering，No. SKLGIE 2014-M-1-1.

2015-10-16

种洋，硕士生，研究方向为地磁辅助导航，E-mail: chongyang_geodesy@outlook.com。

10.14075/j.jgg.2016.10.003

1671-5942(2016)010-0854-05

P229

A

项目来源：国家自然科学基金(41574010，41274045，41476087)；地理信息工程国家重点实验室开放基金(SKLGIE2014-M-1-1)。