经验模式分解在滚动轴承故障诊断中的应用

赵　磊，夏均忠，王　虎，于明奇，汪治安

( 1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)



经验模式分解在滚动轴承故障诊断中的应用

赵磊1，夏均忠2，王虎2，于明奇1，汪治安1

( 1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)

经验模式分解作为一种自适应的非线性、非平稳性信号分析方法，广泛应用于滚动轴承故障诊断中，但存在模态混淆、本征模式函数的判据、边界效应等问题。首先系统阐述了经验模式分解方法原理及特性，分别对经验模式分解的改进算法固有时间尺度分解、局部特征尺度分解和完备总体经验模式分解作了分析，研究了其基本原理、应用和特点，提出经验模式分解与其他诊断方法相融合是滚动轴承故障诊断的研究方向。

滚动轴承；经验模式分解；固有时间尺度分解；局部特征尺度分解；完备总体经验模式分解

滚动轴承在旋转机械上主要起支撑作用，即支撑回转体进行更高精度的旋转，同时有方便装配、减少摩擦、延长机械寿命、效率高等优点，因此应用较为普遍。滚动轴承在故障初期损坏较为轻微，不易被人们发现。由于发现不及时，往往会出现停机现象甚至造成设备不应有的损坏，因此，对滚动轴承的早期故障进行诊断具有十分重要的意义。

目前用于滚动轴承故障诊断的方法有很多，如小波理论、随机共振理论[1]、循环平稳理论[2]、经验模式分解等。经验模式分解(empirical mode decomposition，EMD)是Huang N E等[3]在对瞬时频率进行了深入研究后提出来的，并对瞬时频率作了合理的定义和有物理意义的求解，迅速地运用到地震学、水波研究以及机械设备故障诊断[4]等领域。本文对该方法做了研究与分析，并在此基础上介绍了固有时间尺度分解(intrinsic time-scale decomposition，ITD)、局部特征尺度分解(local characteristic-scale decomposition，LCD)和完备总体经验模式分解(complete ensemble empirical mode decomposition，CEEMD)等改进算法的基本原理、应用和特点。

1　经验模式分解(EMD)

Huang N E等对瞬时频率作了深入研究后发现，只有满足一定条件的信号才能求得具有物理意义的瞬时频率，并将此类信号称为本征模式函数或基本模式分量(intrinsic mode function，IMF)。IMF需要满足两个条件：①在整个时间序列内，极值点数量与过零点数量必须相同或最多相差不超过一个；②由局部极大、极小值点确定的包络线的均值为零。

EMD分解的基本原理[5]：

(1)假设原始信号为x(t)，通过对所有局部极值点进行三次样条插值运算，求得其上下包络局部均值序列为m(t)。

(2)令h1(t)=x(t)-m(t)，若h1(t)满足IMF的两个条件，则将其作为第一个IMF分量；否则，将h1(t)作为原始数据重复以上步骤k次，得h1k(t)=h1(k-1)(t)-m1k(t)，使h1k(t)满足IMF条件并获得第一个IMF，记为c1(t)=h1k(t)。

(3)从x(t)中去除c1(t)，得到残差r1(t)：

r1(t)=x(t)-c1(t)

(1)

把r1(t)作为新的“原始”信号重复以上步骤，以此循环，当rn(t)为单调函数不能再筛选出IMF分量时停止，得到n个IMF分量。最终将原始信号x(t)分解为n个IMF分量和一个残余函数(代表信号的平均趋势)：

(2)

通过把滚动轴承振动信号的基本模式分量准确地筛选出来，然后计算求出其瞬时频率并进行时频分析，进而判断轴承的运行状态是否出现故障。

文献[6]针对滚动轴承的状态监测和故障诊断中振动信号的非平稳性，提出了一种基于经验模式分解和Fisher判别分析(FDA)的滚动轴承故障诊断方法。文献[7]通过对比多种抑制EMD端点效应的延拓方法，对滚动轴承进行故障诊断，提出了EMD端点效应抑制方法评价指标，并得出镜像延拓法为相对最优方法。文献[8]在传统包络分析的基础上，利用EMD进行分解并选择适当的IMF分量进行包络分析，从而提取滚动轴承故障特征进行诊断分析。

EMD作为一种直接针对数据和不需预先确定分解基的非线性非平稳性信号分析方法，具有完备性、正交性和自适应性等优点，可以应用于滚动轴承故障诊断。但这种方法也有需要改进的地方，比如，边界效应、不完全包络、模态混淆问题等。

2　固有时间尺度分解(ITD)

ITD方法是由Mark G Frei和Ivan Osorio于2007年提出的一种自适应的时频分析法，将非平稳复杂信号分解为具有实际物理意义的固有旋转分量(proper rotation component，PRC)和一个单调趋势项[9]。与EMD方法相比，ITD方法在提高计算速度和抑制端点效应方面具有明显的优势，且避免了EMD中的包络误差。

ITD方法的具体分解过程：

(1)假设Xt为一实值信号，t≥0，{τk,k=1,2,…，n}是信号Xt中局部极值点所对应的时刻，令τ0=0。定义L为Xt的基线提取因子，将信号Xt分解为固有旋转分量Ht和基线分量Lt，即

Xt=LXt+(1-L)Xt=Lt+Ht

(3)

式中：Lt=LXt为基线分量；Ht=(1-L)Xt为固有旋转分量，表示信号中的局部相对高频成分。

(2)令Xk=X(τk)，Lk=L(τk)。假设在[0，τk]上定义了Lt和Ht，Xt在[0，τk+2]上有定义，则在(τk，τk+1]上可定义该分段线性基线提取因子L为

(4)

(1-α)Xk+1

(5)

式中α为PRC幅度的线性比例，取值范围为(0，1)，通常取0.5。

(3)求得固有旋转分量Ht：

Ht=(1-L)Xt=Xt-Lt

(6)

基线分量Lt保留了各个极值点之间的单调性，同时还保留了叠加在这个基线上的包络。将基线分量当成新的原始信号重复以上的操作，如此循环可得到一系列的固有旋转分量，直到得到一个单调趋势项。将原始信号Xt分解成若干个不同频率段的固有旋转分量之和与一个单调趋势项。整个过程表示为

(7)

与EMD以及传统的信号分析方法相比，ITD算法的优势主要体现在：

①在信号被分解为固有旋转分量的过程中，没有EMD分解过程中复杂的筛选和样条插值，降低了计算的复杂度，同时还可以实时获得信号的瞬时参数，是一种高速的信号处理方法。

②通过ITD分解得到各个瞬时参数能够精确地表达非平稳信号频率时变的特性(时频信息的瞬时时间分辨率等于输入信号中极值点所对应的时间尺度)，与传统的积分变换得到瞬时参数信息相比，时频信息不受时频不确定性制约。

文献[10]针对滚动轴承的非线性和非平稳振动信号中提取故障特征难的问题，在ITD的基础上，结合模糊熵的概念，提出了一种基于改进的ITD和模糊熵的滚动轴承故障诊断方法。文献[11]为了有效地提取滚动轴承故障特征信息并实现滚动轴承故障的精确诊断，提出了一种基于ITD和峭度准则的包络解调方法。

然而，ITD方法缺少对算法本身及PRC分量的物理意义具体论述，同时该方法采用线性变换分解的信号波形可能会出现毛刺并失真。

3　局部特征尺度分解(LCD)

为克服ITD分解结果出现的失真现象，程军圣等[12]在有机融合了EMD和ITD核心思想的基础上，定义了瞬时频率具有物理意义的单分量信号——内禀尺度分量(intrinsic scale component，ISC)，提出了一种新的自适应分解方法——局部特征尺度分解。

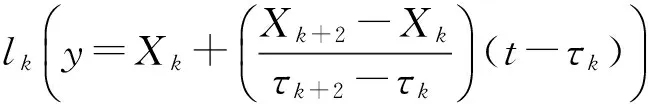
(8)

(9)

这两个条件不仅可以保证相邻极值点之间的单调性，也保证分解得到的波形的光滑性与对称性，使得每个分量在任意相邻的极值点之间模态的单一性，且在局部可以与正弦曲线相吻合，从而使得瞬时频率具有物理意义。

LCD 方法的分解步骤：

(1)对于实信号Xt(t≥0)，确定Xt的极值点(τk，Xk)(k=1，2，…，M)，并计算：

(10)

式中Ak如式(9)所定义。

(2)由于Lk的值是从2到M-1，需要对序列进行延拓来估计端点L1、LM的值，得到左右两端极值点(τ0，X0)、(τM+1，XM+1)。令k分别等于0和M-1，按式(10)求出L1与LM的值，再对所有的Lk(k=1，2，…，M)进行三次样条插值得到均值曲线BL1(t)。

(3)将均值曲线从原信号中分离出来：

h1(t)=Xt-BL1(t)

(11)

若h1(t)满足ISC分量的条件，输出h1(t)并令ISC1=h1(t)。否则将h1(t)作为原始数据，重复上述步骤，直到h1k(t)是一个ISC分量，记作ISC1=h1k(t)。

(4)从原始数据中分解出ISC1分量：

u1(t)=Xt-ISC1

(12)

由此得到一个新的剩余信号u1(t)。

(5)再将u1(t)视为原始数据，重复步骤(1)—(4)，重复循环n-1次，直到剩余信号un(t)为一单调函数为止，得到

(13)

LCD分解过程中采用三次样条拟合来代替线性变换，克服了ITD算法中线性变换分解结果出现的失真现象，而且定义的均值曲线只采用一次三次样条拟合，与EMD方法中采用两次三次样条拟合相比，LCD的拟合误差和计算时间相对较小。

文献[13]针对机械系统的复杂性、振动信号的随机性和动力学突变行为表现在不同尺度上，提出了基于局部特征尺度分解和排列熵的滚动轴承故障诊断方法。文献[14]利用测量振动信号的复杂性和反映内在复杂性的振荡变化，提出了基于LCD和模糊熵的滚动轴承故障诊断方法。文献[15]对不同工作状态和故障类型下的滚动轴承振动信号进行了分析，提出了基于LCD-Hilbert 谱奇异值和分位数回归的多变量预测模型模式识别方法的滚动轴承故障诊断方法。

LCD虽然解决了EMD、ITD等方法存在的部分问题，但不能避免模态混淆现象，难以区分频率接近的分量，而且无法验证各个ISC分量之间的正交性。因此，对LCD方法还需进一步深入研究。

4　完备总体经验模式分解(CEEMD)

2011年Torres等提出了完备总体经验模式分解[16]。它在分解的每个阶段都添加一个特定噪声，并且计算一个唯一残差以得到每个模态，能够提供原始信号的精确重构、更好的模态频谱分离、更少的迭代次数和更低的计算成本。

CEEMD的分解步骤和原理：

(1)设x是目标信号，使用不同的噪声进行EMD分解过程I次，计算总体平均值并定义为IMF1，即

(14)

式中：wi为有单位方差的零均值高斯白噪声；εk为允许在每个阶段选择信噪比。

计算一阶残差：

r1=x-IMF1

(15)

(2)继续分解实现r1+ε1E1(wi)，i=1，2，…，I，直到满足第一个IMF条件，并定义第二个IMF：

(16)

(3)计算k阶残差：rk=rk-1-IMFk，k=2，3，…，K，然后提取rk+εkEk(wi)的第一个IMF分量，其中i= 1，2，…，I，并计算得到IMFk+1：

(17)

(4)继续筛选直到获得的残差不能再被分解为止(残差最多不超过两个极值)，得到

(18)

式中：R为最终残差；K为IMF的总数。

所以，目标信号x可表达为

(19)

文献[17]针对地震信号的非平稳性和去噪方法对非平稳信号的适应性，提出了基于CEEMD的地震数据小波阈值去噪方法。而同样作为非平稳、非线性的滚动轴承振动信号从理论上也可以应用CEEMD进行故障诊断，是一种比较新颖的故障诊断方法。

CEEMD是一种自适应的信号处理方法，保持了EMD方法的完备性，适用于处理复杂的非平稳非线性信号。能够部分克服EMD的模态混淆现象，使原始信号通过IMFs相加得到准确重建。但是，由于CEEMD是由直接消除含噪IMF的方法进行分解的，所以存在损失有效信号的风险。

5　结　论

(1)EMD作为一种直接针对数据和不需预先确定分解基的非线性非平稳信号分析方法，具有完备性、正交性和自适应性等优点，从根本上摆脱了传统诊断方法的局限性。

(2)ITD 在提高计算速度和抑制EMD 端点效应方面具有明显的优势，能够避免EMD中的包络误差。

(3)LCD克服了ITD 对信号进行的线性变换分解结果出现的失真现象，且LCD中均值曲线的定义只采用一次三次样条拟合，与EMD相比，LCD的拟合误差相对较小且计算时间少。

(4)CEEMD能够部分克服 EMD 的模态混淆现象，通过 IMFs 相加可以得到准确重构，不仅吸收了小波变换多分辨的优点，而且克服了小波基选取的困难，能够准确地反映信号能量在各种尺度上的分布规律。

(5)随着滚动轴承故障诊断技术的不断完善与发展，单一的诊断技术已经不能满足复杂的振动信号处理要求，为了提高诊断的效率和精度，未来的发展方向将是多种诊断技术的混合运用。EMD和频谱分析技术、共振解调技术、随机共振理论、循环平稳理论、STFT[18]等方法融合起来，并结合各种模式识别技术，如神经网络[19]、支持向量机、模糊理论等，是滚动轴承故障诊断的研究方向。

[1]夏均忠,刘远宏,马宗坡,等.基于调制随机共振的微弱信号检测研究[J].振动与冲击,2012,31(3):132-135.

[2]ZHOU Y, CHEN J, DONG G M, et al. Application of the horizontal slice of cyclic bispectrum in rolling element bearings diagnosis[J]. Mechanical Systems and Signal Processing, 2012,26(1)：229-243.

[3]HUANG N E, SHEN Z, LONG S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London,1998,454(1971):903-995.

[4]GAI G H. The processing of rotor startup signals based on empirical mode decomposition[J]. Mechanical Systems and Signal Processing 2006,20(1):222-235.

[5]ZHAO X M, TEJAS H P，MING J Z. Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J]. Mechanical Systems and Signal Processing, 2012,26(2):712-728.

[6]HU J, LU C, Tao X. Fault diagnosis for rolling bearing based on EMD and FDA[C]. Hongkong:FITMSE，2012:134-139.

[7]曹端超,康建设,赵劲松,等. EMD端点效应抑制方法仿真比较与实例分析研究[J].机械传动,2013,37(3):83-87.

[8]PAN M C, TSAO W C. Using appropriate IMFs for envelope analysis in multiple fault diagnosis of ball bearings[J]. International Journal of Mechanical Sciences, 2013,69(3):114-124.

[9]MARK G F, IVAN O. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proc. R. Soc. A, 2007,46(3):321-342.

[10]郑近德,程军圣,杨宇.基于改进的ITD和模糊熵的滚动轴承故障诊断方法[J].中国机械工程,2012,23(19):2372-2377.

[11]向玲,鄢小安.基于改进ITD和峭度准则的滚动轴承故障诊断方法[J].机床与液压,2015,43(11):178-181.

[12]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法:局部特征尺度分解法[J].振动工程学报,2012,25(2):215-220.

[13]郑近德,程军圣,杨宇.基于LCD和排列熵的滚动轴承故障诊断[J].振动、测试与诊断,2014,34(5):802-806.

[14]ZHENG J, CHENG J, YANG Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy[J]. Mech. Mach. Theory，2013(70): 441-453.

[15]杨宇，何知义，潘海洋,等.基于LCD-Hilbert谱奇异值和QRVPMCD的滚动轴承故障诊断方法[J].振动与冲击,2015,34(7)：121-126.

[16]TORRES M E, COLOMINAS M A，SCHLOTTHAUER G,et al.A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP). IEEE, 2011:4144-4147.

[17]王姣,李振春,王德营.基于CEEMD的地震数据小波阈值去噪方法研究[J].石油物探,2014,53(2):164-172.

[18]ROBERT B R，JEROME A. Rolling element bearing diagnostics-a tutorial[J]. Mechanical Systems and Signal Processing,2011,25(2):485-520.

[19]BIN G F, GAO J J, LI X J, et al. Early fault diagnosis of rotating machinery based on wavelet packets empirical mode decomposition feature extraction and neural network[J]. Mechanical Systems and Signal Processing, 2012,26(3):696-711.

(编辑：张峰)

Application of Empirical Mode Decomposition in Rolling Bearing Fault Diagnosis

ZHAO Lei1, XIA Junzhong2, WANG Hu2, YU Mingqi1, WANG Zhian1

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China；2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

Empirical mode decomposition(EMD), as a self-adaptive nonlinear and non-stationary signal analysis method, is widely used in rolling bearing fault diagnosis. However, there are still some problems for further research such as mode confusion, criterion of intrinsic mode function and endpoint effect. EMD is systematically studied in this paper, and the improved calculating methods, including intrinsic time-scale decomposition(ITD), local characteristic-scale decomposition(LCD) and complete ensemble empirical mode decomposition(CEEMD) are analyzed with an introduction to their basic principles，applications and features. It is pointed out that the combination of EMD with other diagnosis methods will be a new research direction in the rolling bearing fault diagnosis.

rolling bearing; EMD; ITD; LCD; CEEMD

2016-01-07；

2016-01-30.

赵磊(1991—)，男，硕士研究生；

夏均忠(1967—)，男，博士，副教授，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2016.09.011

O32; TN99

A

1674-2192(2016)09- 0049- 05