基于线性拟合的学习者学习模式分析方法研究*

叶竹君　廖志鑫　吴尚宇　王志锋　叶俊民

(1.华中师范大学2013级物理学基地班　武汉　430079)(2.华中师范大学计算机学院　武汉　430079) (3.华中师范大学教育信息技术学院　武汉　430079)



基于线性拟合的学习者学习模式分析方法研究*

叶竹君1廖志鑫2吴尚宇2王志锋3叶俊民2

(1.华中师范大学2013级物理学基地班武汉430079)(2.华中师范大学计算机学院武汉430079) (3.华中师范大学教育信息技术学院武汉430079)

论文提出了一种基于线性拟合的学习者学习模式分类方法。定义了课程教学模型及其基础服务;采用以调查表为主的混合方法,采集并量化了线下数据,以实现这些数据的计算,并通过计算的结果预测学习者趋势;实证方法的结果表明,论文方法能有效预测出学习者的学习趋势。

学习模式; 数据分析; 线性拟合

Class NumberG434

1　引言

在2011年的学习分析技术与知识会议(Learning Analytics and Knowledge,LAK)上,首次提出[1]了学习分析技术的概念,该技术可用于收集、分析与学习者学习行为和学习环境有关的数据集,这些数据既可以是线上数据,也可以是线下数据。

在国外,在2010年,美国新媒体联盟等单位提出的《地平线报告》首次预测学习分析技术会逐渐兴起[2],并且量化学习将成为学习分析的应用趋势之一[3]。随后,学习分析技术出现在对自我反思性学习的量化处理中[4],一方面能对高危学习者的预测,从而帮助学习者避免学业的失败[5],另一方面应用学期数据来估计课程资源利用与学习者评价之间的关系[6]。这些研究和应用,充分体现出了学习分析技术的价值。

在国内,莫景祺[7]认为实施课堂教学评价的目的是诊断和改进教学,因此要重视对评价结果的解释和运用。刘刚[8]提出对评价功能,评价主体、评价标准以及评价结果的分析,有助于把握课堂教学评价改革的基本方向。但这些课堂教学评价的研究中没有明确提出如何对评价结果进行进一步分析和运用。定量分析学习者数据的具体方法如PADClass模型,该方法可对学习过程的数据进行采集和描述,但缺乏对于学习者学习状态的整体评价。

从上述研究来看,相关研究主要是集中在线上数据的采集和处理,因为现有技术已经完全支持了这一有意义的工作。但相对于线上数据的采集与处理研究与应用现状,线下数据的使用与处理则远远落后,如以课堂教学数据采集与处理为代表线下数据处理尤其如此。因此,从课堂教学模式角度对学习者的数据进行采集、量化和分析处理,有待深入,而将对这些数据的处理与学习分析技术相结合,则更显得有研究意义与应用的价值。

2　线下学习分析原理

2.1对课程学习的描述

首先,需要根据目标课程以及课程知识体系结构等方面,研究和设计课程学习模型。本研究基于课程中的知识单元这一角度展开,将某一课程的学习模型所涉及的学习活动分为课内和课外两部分活动。

课内学习活动包括课堂听讲、回答问题、考勤等活动,而课堂听讲主要由有效听课时间来刻画;回答问题由学习者对教师课堂内所问题的回答情况来刻画,而学习者的考勤则依据点名记录来实现考察。在课程学习模型中,这些内容的重要程度可以用对其设置相应权重的方式来加以刻画。

课外学习活动则通常包括平时作业、上机实验、自修等活动,其中作业由学习者课后作业的完成情况及效果来评分;上机实验由教师通过实验完成情况的判定来评分;自修情况则主要对学习者的课后预习、复习等情况进行评价。这些内容的重要程度同样用权重来加以刻画。

2.2学习数据的计算方法

为了定义针对学习数据的计算方法,本文需要定义如下参数:N表示课程数目;m表示学习者数目;t表示知识单元数目;p表示活动数目;Scorequestion_answer表示课堂回答问题成绩;Scoreattendance表示考勤活动成绩;Dataattention_evaluation表示课堂听讲评价数据;Scorehimework表示作业成绩;Scoreexperiment表示实验成绩;Datareview_prepare_evaluation表示复习预习评价数据;Weightinclass表示课内教学活动权重;Weightoutclass表示课外教学活动权重;Weightlistening表示课堂听讲成绩权重;Weightanswer_questions表示课堂回答问题活动成绩权重;Weightattendance表示考勤活动成绩权重;Weighthomework表示作业成绩权重;Weightexperoment表示实验成绩权重;Weightreview_prepare表示复习预习成绩权重;Pointweight_knowledge[i][j]表示知识单元j的权重;Valuestudent_learning_effect_average_evaluation_kn表示学习者K的知识单元j的学习效果评价值;Valuestudent_learning_effect_average_evaluation_kn表示班级学习者知识单元j的平均学习效果评价值;Valuestudent-learning_effect_average_evaluation[i][k]表示学习者k的课程i的平均学习效果评价值。

基于上述参数定义,先设计所需用到的核心计算过程,具体步骤如下。

1) 设置课程教学模型中的各指标权重

(1)教学活动模型的权重设置

课内教学得分权重为Weightinclass;课外教学得分权重为Weightoutclass。要求这些权重之和为1。

(2)课内教学活动的权重设置

听讲得分权重为Weightlistening;回答问题得分权重为Weightanswer_questions;考勤得分权重为Weightattendance。要求这些权重之和为1。

(3)课外教学活动的权重设置

作业得分权重为Weighthomework;实验得分权重为Weightexperoment;复习预习得分权重为Weightreview_prepare。要求这些权重之和为1。

(4)课程i知识单元的权重设置

2) 建立学习效果评价计算规则

假设学习效果评价值的取值范围为0～100之间的实数。具体的计算规则定义如下。

(1)任一个知识单元的学习效果评价值计算规则,如式(1)所示。其中p表示课内学习活动数目,q表示课外学习活动数目。

Valuestudent_learning_effect_evaluation[k][j]=

Weightinclass×(Weightlistening×Dataattention_evaluation

+Weightattendance×Scoreattendance

+Weightanswerquestions×Scorequestion_answer)

+Weightoutclass×(Weighthomework

×Scorehomework+Weightexperiment

×Scoreexperiment+Weightreview_prepare_evaluation)

(1)

(2)班级学习者的知识单元j的平均学习效果评价值计算规则,如式(2)所示。

Valuestudent_learning_effect_average_evaluation_knowledge[j]=

(2)

(3)学习者k的课程i的平均学习效果评价值计算规则,如式(3)所示。

Valuestudent_learning_effect_average_evaluation_knowledge[j][k]=

×Pointweight_knowledge[j])]÷n

(3)

(4)班级学习者课程i的平均学习效果评价值计算规则,如式(4)所示。

?Valuestudent_learning_effect_average_evaluation_class[i]=

(4)

(5)将上述(1)～(4)中的所有计算结果保存起来,以方便学习者学习趋势的分析。

2.3数据采集策略与方法

针对具体课程的课堂教学数据(即对线下数据采集)采集,本文的主要策略和方法是:问卷调查方式;问卷调查与网站监控行为结合的方式[9]。在线下数据的具体采集过程中,为了解决好所采集到的数据存在完备性、主观性等问题,本研究采用人工方式对这些数据进行采集,并在此基础上进行检测和验证。

现在以采集学习者课堂表现数据为例,说明部分线下数据的具体采集做法。这一做法是,一方面,通过采用现场录像和回放分析的方式采集这些数据,再通过采用人工标注的方式采集有效听课时间,同时记录学习者在学习过程中的表情、动作和认知情况,事后可以将这些数据量化;另一方面,在采集这些数据的同时可以进行数据的确认工作,在保障数据的完备性的同时,尽可能减少由于人为主观性所带来的对采集数据的干扰。

除此之外,本研究还使用了表情分析工具来辅助收集部分数据,并在这类工具的帮助下,解决自动完成标注部分有效听课时间等问题,同时结合表情分析算法自动采集学习者学习过程中的部分表情、动作、认知和心理数据。

实践表明,这些方法的综合应用,可较准确的获取学习者的心理与认知方面的数据,这解决了这类数据不易采集的问题。

2.4学习者学习模式分类方法

由于学习者学习模式分类结果,可以用学习者的学习趋势来表达,如某一学习者在学习模式分类时是被划分到了属于学习成绩(分数)很差的范畴内,则其对应的学习趋势可以表示为在一段时间内为在很差的范畴内保持着稳定这一趋势。因此,我们可首先按照学习者的知识单元学习效果评价值对学习者进行排名,得到每个学习者在每个知识单元的排名;其次,对某一个学习者在所有知识单元中排名的变化情况进行研究。

具体的做法是,以学习知识单元为X轴,该知识单元学习效果评价值的排名为Y轴,在直角坐标系中绘制某个学习者所有的知识单元的学习排名的散点图。对每个散点图中的散点进行拟合,可以得到所拟合出来的线性回归直线方程,利用该方程,可以分析出学习者的整体升降趋势。计算每个线性回归方程的拟合度,所用的相关公式如(5)所示。

(5)

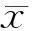
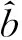
3　实证研究

本文以《大学物理》课程为例进行实证研究,采样对象为某本科专业两个班级的学生。通过统计分析,可知这些学习者的成绩分布的一种典型情况为:30%的学习者成绩优秀,40%的学习者成绩中等,20%的学习者成绩较差,10%的学习者成绩非常差。对这些学习者的样本学习数据,依据真实性、完整性和规范性原则进行清理和筛选后,从不同学习层次的学习者中共选择10名学习者的学习数据,依据本文方法进行实证研究。

现以学习者S3的学习数据为例加以说明,假设该生的课程学习排名数据用元组(知识单元序号,知识单元排名)进行描述,其具体信息是(1,6),(2,6),(3,6),(4,6),(5,7),(6,8)。依据这些信息可拟合所得的代表该生学习趋势的直线方程,该方程表示了该学生课程学习过程趋势,经过计算可知该生的学习趋势为呈现出稳定上升的趋势。

4　结语

本文提出了一种基于线性拟合的学习者学习模式分类方法,对传统教学过程中的线上数据进行了采集和分析,以实现针对这些数据的计算,并通过计算的结果可以预测学习者趋势。通过实证研究,说明了该方法的可行性。进一步的研究想法是,可以将线上数据分析和线下数据分析结合起来,可以更准确地刻画该学习者的学习趋势。

[1] 学习分析技术与知识国际会议.学习分析和知识[EB/OL].[2012-05-02]. http://lak12.sites.olt.ubc.ca/.

LAKE2012.Learning Analytics and Knowledge[EB/OL].[2012-05-02]. http://lak12.sites.olt.ubc.ca/.

[2] 新媒体联盟.2011-地平线-报告-K12[DB/OL].

The New Media Consortium(NMC). 2011 -Horizon -Report -K12[DB/OL].

[3] 新媒体联盟.2015-地平线-报告-K12[DB/OL].

The New Media Consortium(NMC). 2015 -Horizon -Report -K12[DB/OL].

[4] Verónica Rivera-Pelayo, Valentin Zacharias, Lars Müller, et al. Applying Quantified Self Approaches to Support Reflective Learning[OL]. LAK,2012.

[5] Annika Wolff, Zdenek Zdrahal, Andriy Nikolov, et al. Improving retention: predicting at-risk students by analysing clicking behaviour in a virtual learning environment[C]//LAK,2013.

[6] Richard Joseph Waddington, SungJin Nam. Practice Exams Make Perfect: Incorporating Course Resource Use into an Early Warning System[C]//LAK,2014.

[7] 莫景祺.教师如何实施课堂教学评价[J].课程·教材·教法,2008(11):14-18.

MO Jingqi. The National Center for School Curriculum and Textbook Development[J]. Curriculum, Teaching Material and Method,2008(11):14-18.

[8] 刘岗,田静.课堂教学评价改革中的几个基本问题[J].山西师大学报:社会科学版,2012(1):144-147.

LIU Gang, TIAN Jing. Research Institute of Science and Teaching[J]. Journal of Shanxi Normal University, 2012(1):144-147.

[9] 王征,谭龙江.基于客户心理挖掘和预测的推荐系统[J].计算机工程与设计,2012,33(11):4347-4350.

WANG Zheng, TAN Longjiang. Based on the recommendations from the customer psychological excavation and forecasting system[J]. Computer Engineering and Design,2012,33(11):4347-4350.

Analysis Method of Learners’ Learning Patterns Based on Linear Fitting

YE Zhujun1LIAO Zhixin2WU Shangyu2WANG Zhifeng3YE Junmin2

(1. State-based Physics Class, 2013, Central China Normal University, Wuhan430079) (2. School of Computing, Central China Normal University, Wuhan430079) (3. School of Education Information Technology, Central China Normal University, Wuhan430079)

In this paper, a method based on linear fitting is proposed to categorize learners’ learning patterns. Curriculum teaching model and its basic services are defined. Then the offline data are collected and processed quantitatively by different methods, with questionnaire as an important one, to translate a variety of meaningful data into numerical data which can be processed. The results of calculation are used to discover the learners’ learning patterns. Finally, the proposed method is verified through empirical approach. The results from our experiments indicate that the linear fitting method can describe the learners’ learning patterns more effectively.

learning patterns, data analysis, linear fitting

2016年3月8日,

2016年6月27日

教育部人文社会科学研究规划基金项目(编号:15YJA880095)资助。

叶竹君,女,研究方向:教育大数据应用。廖志鑫,男,研究方向:教育大数据应用。吴尚宇,男,研究方向:教育大数据软件开发。王志锋,男,博士,讲师,研究方向:教育信息技术。叶俊民,男,博士,教授,研究方向:软件工程与教育大数据应用。

G434DOI:10.3969/j.issn.1672-9722.2016.09.028