基于噪声的GBCD算法理论研究*

李　锐　李静静

(1.河南师范大学数学与信息科学学院　新乡　453007)(2.河南师范大学附属小学　新乡　453007)



基于噪声的GBCD算法理论研究*

李锐1李静静2

(1.河南师范大学数学与信息科学学院新乡453007)(2.河南师范大学附属小学新乡453007)

压缩感知; 贪婪块坐标下降算法; 有限等距性质

Class NumberTP301

1　引言

在阵列信号处理中,窄带信号的波达估计(Direction of arrival,DOA)是研究的重要领域之一,已有诸多算法提出[1～3]。然而,当信噪比低、快照数据少或点源密集的情况下,这些算法的效果不理想。为解决该类问题,文献[4]提出基于块坐标下降的贪婪块坐标下降算法(Greedy Block Coordinate Descent,GBCD),该算法把波达估计DOA看作多重测量向量模型(Multiple Measurement Vectors,MMV):

min‖X‖2,1s.t.Y=AX

(1)

Y=AX+E

(2)

其中Y∈Rm×t是带有噪声的观测矩阵,A∈Rm×n(m≼n)是已知感知矩阵,X∈Rn×t是未知K-稀疏信号,它的支撑集是Ω并且|Ω|=K,E∈Rm×t是噪声矩阵。噪声类型有: 1)l2边界噪声,‖E‖2≤ε; 2)l∞边界噪声,‖AE‖∞≤ε; 3) 高斯噪声,Ei∽N(0,σ2)[5～9]。本文考虑的是1)类型噪声。

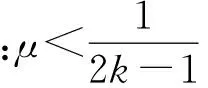
2　问题描述

GBCD算法过程如下:

算法1:GBCD输入:A,Y,X(0)=0,n=1,λ,β.1:开始循环2:for i=1:ndo3:Pi(k-1)=Xi(k-1)-βATi(AX(k-1)-Y)4:Xi(k)=Pi(k-1)‖Pi(k-1)‖2max(0,‖Pi(k-1)‖2-λβ)5:comp(i)=‖Xi(k)-Xi(k-1)‖6:endfor7:选择指标i0,使得comp(i0)=max(comp)8:X(k)←[X1(k-1);…;Xi0-1(k-1);Xi0(k);Xi0+1(k-1);…;Xn(k-1)]9:k←k+110:结束循环

在文献[1]中,矩阵A满足K阶有限等距性质(Restricted Isometry Property,RIP),如果存在一个常数δ∈(0,1),使得

(3)

对于所有的K阶稀疏向量h,满足该条件的最小常数称为有限等距常数(restricted isometry constant,RIC)记为δK。

文献[13]假设矩阵A满足K阶的δK,S是一个集合,|S|≤K,那么对于任意x∈Rm都有

(4)

3　支撑集恢复的RIP条件

引理1:假设X是K-稀疏矩阵,A满足K+1阶RIP,那么

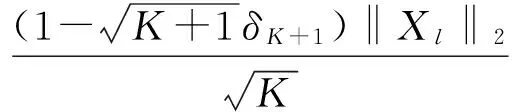
(5)

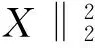
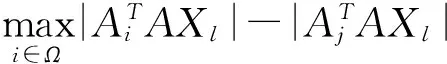
(6)

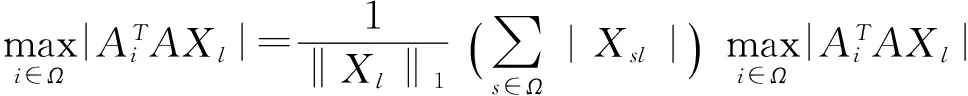
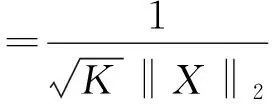
(7)

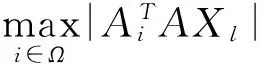
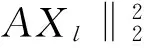
(8)

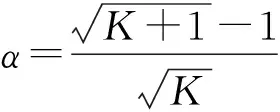
(9)

为了简化符号,令w=αt‖Xl‖2ej∈Rn,这里

那么

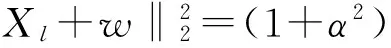
(10)

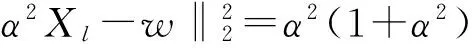
(11)

因此有

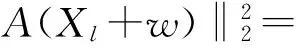
(12)

和

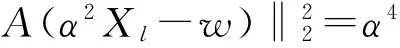
(13)

那么,通过上面式(12)和(13)两个等式可得:

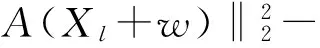
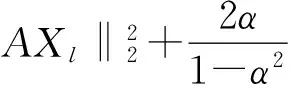
(14)

不难得到:

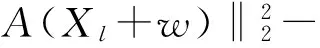
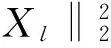
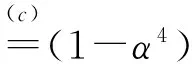
(15)

1) 因为Xl和w分别是K-稀疏向量和1-稀疏向量; 2) 由式(10)～式(11)得到; 3) 由式(9)中第二个等式得到。结合式(14)～式(15)和1-α4>0可得:

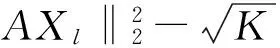
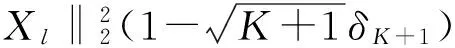
结合式(8)可得:

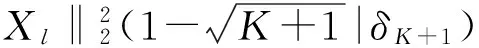
因此,引理1成立。

定理1:假设X是K-稀疏矩阵,它的支撑集是Ω且|Ω|=K,A满足K+1阶RIP,

(16)

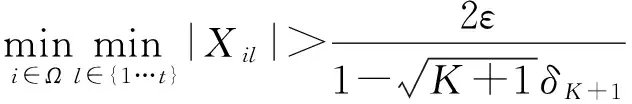
证明:首先,证明在第1轮迭代中GBCD能够选择正确指标。根据算法1中第7、8行,可知证明第一轮GBCD能够选择正确指标等价于证明式(17)成立:

(17)

根据算法中第4、5行和X(0)=0,式(17)等价于:

(18)

(19)

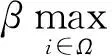
(20)

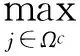
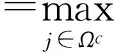
(21)

结合式(20)和式(21)得:

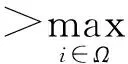
(22)

式(22)左边:

(23)

由引理1得到。式(22)右边:

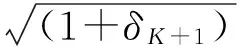
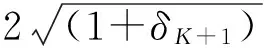
(24)

由‖E‖2≤ε得到。结合式(23)和式(24)可得:

由引理1可知在算法的第1轮迭代中,GBCD能够选择正确指标,即恢复支撑集。

其次,假设在前k-1轮能够精确恢复,2≤k≤|Ω|。现在证明GBCD在第k轮能够精确恢复支撑集,由算法1中第5、7、8行可知,等价于证明式(25)成立:

(25)

由算法1中第4、5行可知,证明式(25)成立等价于证明式(26)成立:

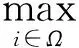
-Xi(k-1)‖2)

-λβ)-Xj(k-1)‖2)

(26)

-λβ)-Xj(k-1)‖2

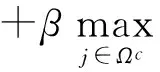
(27)

式(26)的左边:

-λβ)-Xi(k-1)‖2

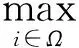
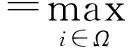
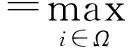
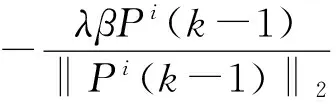
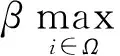
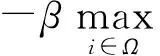
(28)

那么,结合式(27)和(28)得:

(29)

由于X是稀疏矩阵,X(k-1)也是稀疏矩阵,由引理1可知(29)成立,即定理1成立。

4　实验仿真

实验在Intel i5 CPU和4G内存机器上实现。其中,矩阵A是100×1000的随机矩阵,m的取值范围是100～500,变化步长是50,实验误差如图1所示。

图1　实验误差

实验结果显示:在噪声的情况下,GBCD仍然能够精确恢复稀疏信号的支撑集。

5　结语

[1] Ko YH, Kim YJ, et al. 2-D Doa estimation with cell searching for a mobile relay station with uniform circular array[J]. IEEE Trans Communications,2010,58(10):2805-2809.

[2] 金梁,殷勤.时空DOA矩阵方法[J].电子学报,2000,28(6):8-13.

JIN Liang, YIN Qinye. Space-Time DOA Matrix Method[J]. Acta Electronica Sinica,2000,28(6):8-13.

[3] 何子述,黄振兴,向敬成.修正MUSIC算法对相关信号源的DOA估计性能[J].通信学报,2000,21(10):14-17.

HE Zishu, HUANG Zhenxing, XIANG Jingcheng. The performance of DOA estimation for correlated signals by modified MUSIC algorithm[J]. Journal of China Institute of Communications,2000,21(10):14-17.

[4] X. Wei, Y. Yuan, Q. Ling. DOA estimation using a greedy block coordinate descent algorithm[J]. IEEE Trans. Signal Process,2012,60(12):6382-6394.

[5] J. J. Fuchs. Recovery of exact sparse representations in the presence of bounded noise[J]. IEEE Trans. Inf. Theory,2005,51(10):3601-3608.

[6] D. L. Donoho, M. Elad, V. N. Temlyakov. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Trans. Inf.Theory,2006,52:6-18.

[7] E. J. Candes. The restricted isometry property and its implications for compressed sensing[J]. C. R. Acad. Sci. Paris, Ser. I,2008,346(11):589-592.

[8] T. Cai, L. Wang. Orthogonal matching pursuit for sparse signal recovery with noise[J]. IEEE Trans. Inf. Theory,2011,57:4680-4688.

[9] E. J. Candes, T. Tao. The dantzig selector: Statistical estimation when p is much larger than n[J]. Ann. Statist,2007,35:2313-2351.

[10] Li Haifeng, Fu Yuli, Hu Rui, et al. Perturbation analysis of greedy block coordinate descent under RIP[J]. IEEE Trans. Signal Process,2014,21(5):518-522.

[11] Li Haifeng, Ma Yingbin, Liu Wenan, et al. Improved analysis of greedy block coordinate descent under RIP[J]. Electronics Letters,2015,51(6):488-490.

[12] D. Needel, J. A.Tropp. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis,2009,26(3):301-321.

Analysis of GBCD Based on Noise

LI Rui1LI Jingjing2

(1. College of Mathematics and Information Science, Henan Normal University, Xinxiang453007) (2. Affiliated Primary School of Henan Normal University, Xinxiang453007)

compressed sensing, greedy block coordinate descent, restricted isometry property

2016年3月9日,

2016年4月18日

李锐,女,硕士研究生,助理实验师,研究方向:信息处理。李静静,女,研究方向:统计学。

TP301DOI:10.3969/j.issn.1672-9722.2016.09.007