一类在Box Splines空间中封闭曲面的重构算法*

郭　旺　路　游

(中国石油大学(北京)地球物理与信息工程学院　北京　102249)



一类在Box Splines空间中封闭曲面的重构算法*

郭旺路游

(中国石油大学(北京)地球物理与信息工程学院北京102249)

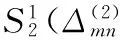
Box样条; 亏格; 拟插值算子; 边界宽度重合; 封闭曲面重构

Class NumberTP391.7

1　引言

封闭曲面重构技术已经被广泛应用于计算机辅助几何设计、计算机图形学、计算机可视化等众多领域。到目前为止,已有大量文献对封闭曲面重构进行了研究,其成果已经应用到了诸多领域,如医学成像中的人体器官曲面(心脏、肺、膀胱、肾等)[3]以及以地球曲面作为模型的地球物理学和气象学的曲面[4]等。

随着各领域对三维数据拟合技术的要求越来越高,基于特定技术的现有方法[6～11]不但不能满足各领域的新需求,而且分别存在各自的缺陷,例如基于Bezier曲面的重构方法不能实现局部的控制修改,任意控制顶点移动,曲面上各个部分都会随之改动,无法进行局部修改;基于B样条曲面的重构方法虽然保留了Bezier方法的优点,同时对局部修改进行了改进,增强了局部控制的灵活性和光滑拼接性,但是只能近似表示圆锥曲线和初等解析曲面,无法得到精确结果;NURBS方法弥补了B样条方法的不足,但是单一的NURBS曲面只能表示简单拓扑结构上的曲面(如一个平面、圆柱或者圆环面的曲面),不能表示任意拓扑结构的曲面,且张量积的基函数又会使曲面的次数升高,降低效率。同时,经过大量研究和实验发现,上述重构方法在解决曲面封闭问题上难度极大,需要运用复杂技术才能勉强实现,从而降低了封闭曲面的重构效率,也逐渐缩小了其应用领域范围。因此,研究新算法、开发新技术用来高效率、高精度地实现封闭曲面的重构已经成为亟待解决的问题。

2　封闭曲面上数据点的表示

2.1亏格的定义及其特点

封闭曲面即从曲面上任意一点向这个曲面上任何一个方向出发都能回到这个起点的曲面。根据封闭曲面的特点、性质可以将封闭曲面分为不同类型,而亏格即为封闭曲面的特性之一。为了便于理解,下面给出亏格详细说明。

定义:若曲面中最多可画出n条闭合曲线同时不将曲面分开,则称该曲面亏格为n。

以实体封闭曲面为例,亏格g就是曲面上洞眼的个数。球面没有洞,故亏格g=0,即亏格为零的封闭曲面的最基本形式;环面只有一个洞,故亏格g=1,即亏格为一的封闭曲面的基本形式。

2.2平面参数化映射

平面参数化就是寻求一个线性映射函数F将三维网格模型与二维平面中的拓扑同胚模型联系起来。对空间网格模型中的每个顶点Pi(xi,yi,zi),在二维平面上确定一个与之对应的参数点pi(ui,vi),如图1所示,参数化结果对拟合曲面的质量有重要影响。对参数化结果的基本要求是平面参数域中的三角片集合是有效的,除了有效性要求外,还要求空间三角片与对应的参数域中的三角片在集合特性方面的差异最小。

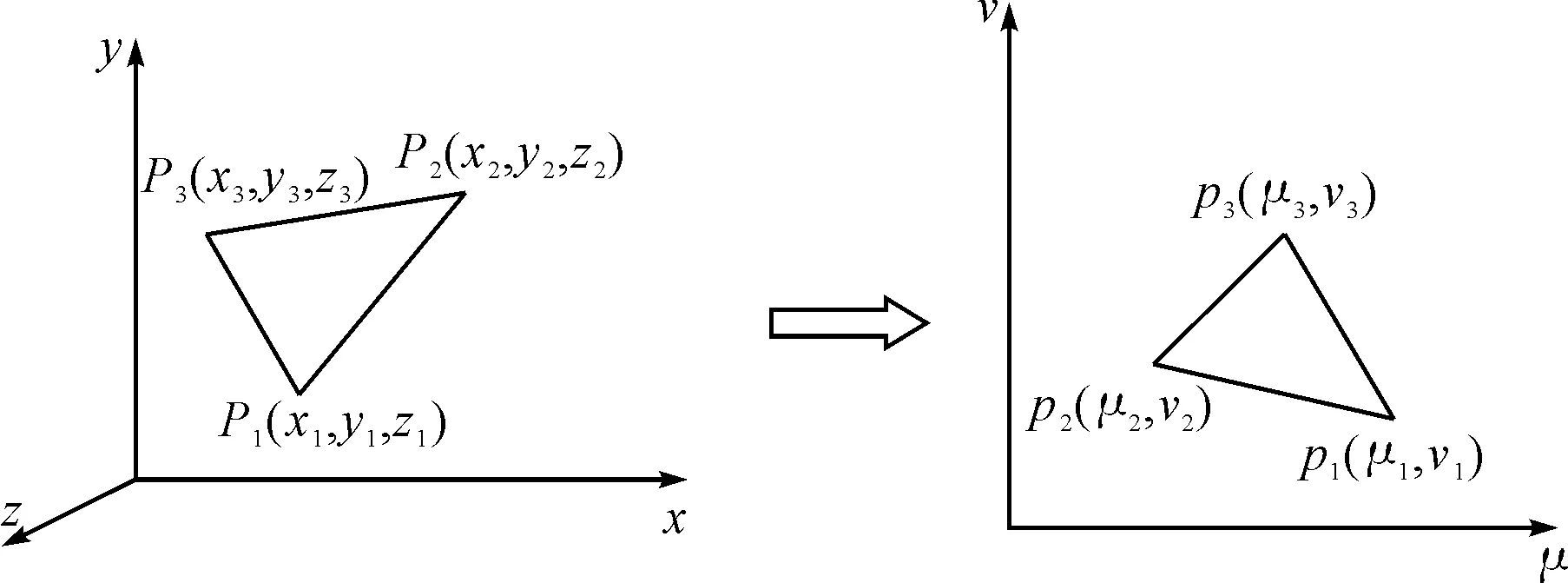
图1　空间三角形到平面三角形的映射

2.3数据点参数化的表示形式

令S是一个闭合曲面,且在闭合曲面上存在一对一或一对多的S的映射,每一个映射都需要构造一个函数F与其对应。假设在S上有一系列散乱数据点P1,…,Pd满足F(Pi)≅ri,i=1,…,d。函数F这样被构造的目的是使相关联的曲面SF={F(s),s∈S}在每个数据点处都存在一个连续变化的切平面,即闭合曲面SF至少是连续的。其定义域等同于矩形域D=I×J,其中I=[0,π]和J=[0,2π],通过映射χ定义如下:

χ:S→D

即(x,y,z)→(θ,φ),x=x(θ,φ),y=y(θ,φ),z=z(θ,φ)。

3　Box样条空间的拟插值算子

不失一般性,在矩形区域D=[0,1]⊗[0,1]上,对矩形域进行均匀的矩形剖分,再连接每个小矩形的两条对角线而形成的均匀三角剖分即为均匀2-型三角剖分(如图2)。其剖分线如下:

mx-i=0,ny-i=0,ny-mx-i=0,

ny+mx-i=0,i=0,±1,±2…

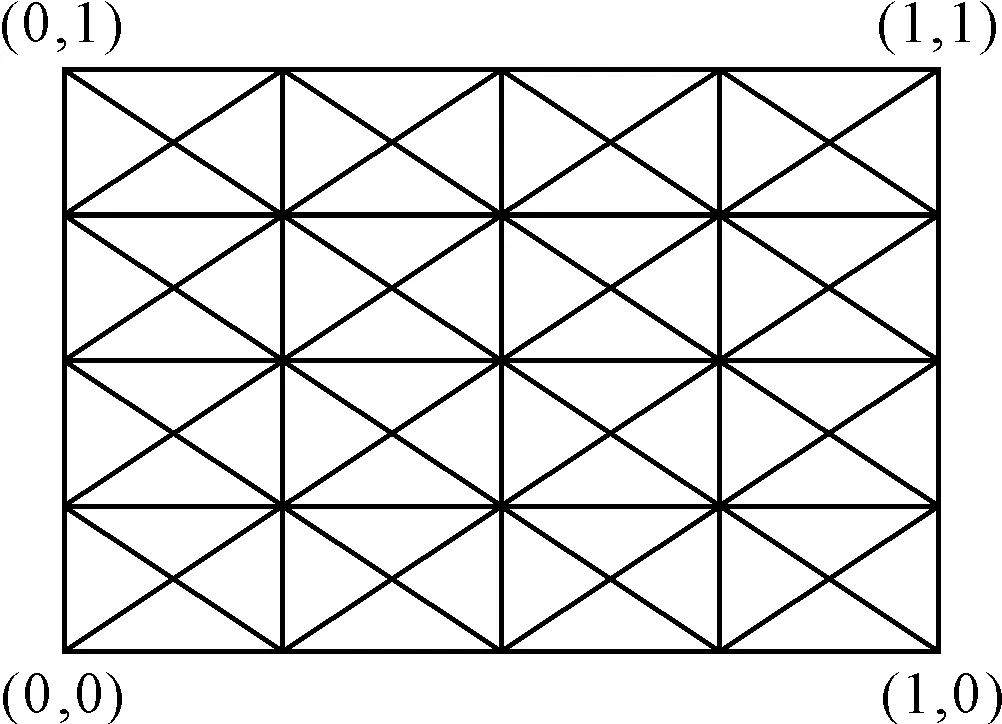
图2　均匀2-型三角剖分

图)的局部支集

根据P.Zwart[1],部分胞腔多项式如下

由对称可以得到其它胞腔多项式,即:

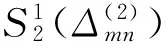
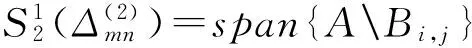
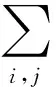
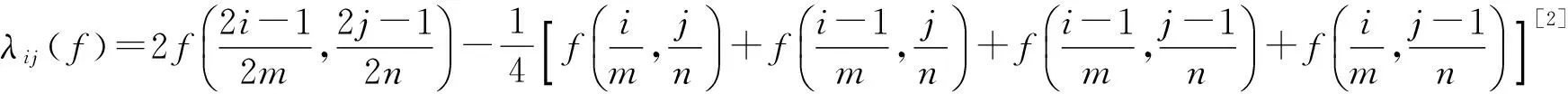
注意上式中的线性泛函λij依赖于函数f在Bi,j(x,y)的支集上5个网点的值。Wmn(f)虽然不是一个线性正算子,但它却有更高的逼近阶。容易证明得到Wmn(f)≡f,当f∈P2。

4　利用拟插值算子Wmn(f)拟合封闭曲面

4.1拟插值算法步骤

Step1:取m×n个采样数据点p(θ,φ),并输入;

Step2:由映射关系(x,y,z)→(θ,φ)得到数据点的参数化表示形式为x=x(θ,φ)、y=y(θ,φ)、z=z(θ,φ);

Step4:由公式,给出λij(f);

Step6:原始区域“边界宽度重合”,并对采样数据点进行拟合,输出重构后的封闭曲面。

对于拟插值算法Step6中提到的“边界宽度重合”,是为了更好地解决“封闭”难题,以实现重构后曲面光滑性强、精确度高的效果,在4.2节中将会给出详细的“边界宽度重合”原理及过程说明。

4.2“边界宽度重合”

以亏格为零的封闭曲面,即球面为例,同样,定义封闭曲面定义域为I×J=[0,π]×[0,2π],通过参数化将数据点转换成极坐标的表示形式,即x=cos(θ)cos(φ),y=cos(θ)sin(φ),z=sin(θ)。

拟合结果显示,没有实现封闭效果。为了解决一类Box Splines空间中的曲面封闭的难题,本文根据拟插值算法的特性,提出了“边界宽度重合”的方法(以下均以亏格为零的封闭曲面为例进行比较分析)。

“边界宽度重合”并非任意添加边界,具体添加原理如下:由2.3节可知,以封闭曲面S为一个球面为例,它可以等同于矩形域I×J=[0,π]×[0,2π],分别将I和J平均分成n和m等份,根据3.1节,若置B(x,y)的支集中心在原点(0,0),则由其平移可产生一系列B样条Bi,j(x,y),并且构成一个元素个数为(m+2)(n+2)的集合。为了便于取点,令所取数据点均在n×m等分线上,则对于任意数据点p,需要平移出9个Bi,j(x,y)而得到,而为了满足边界点处B(x,y)支集的平移需求,需要对原始矩形域进行添加,如图4所示即为原始区域边界点处B(x,y)支集平移过程(部分)。

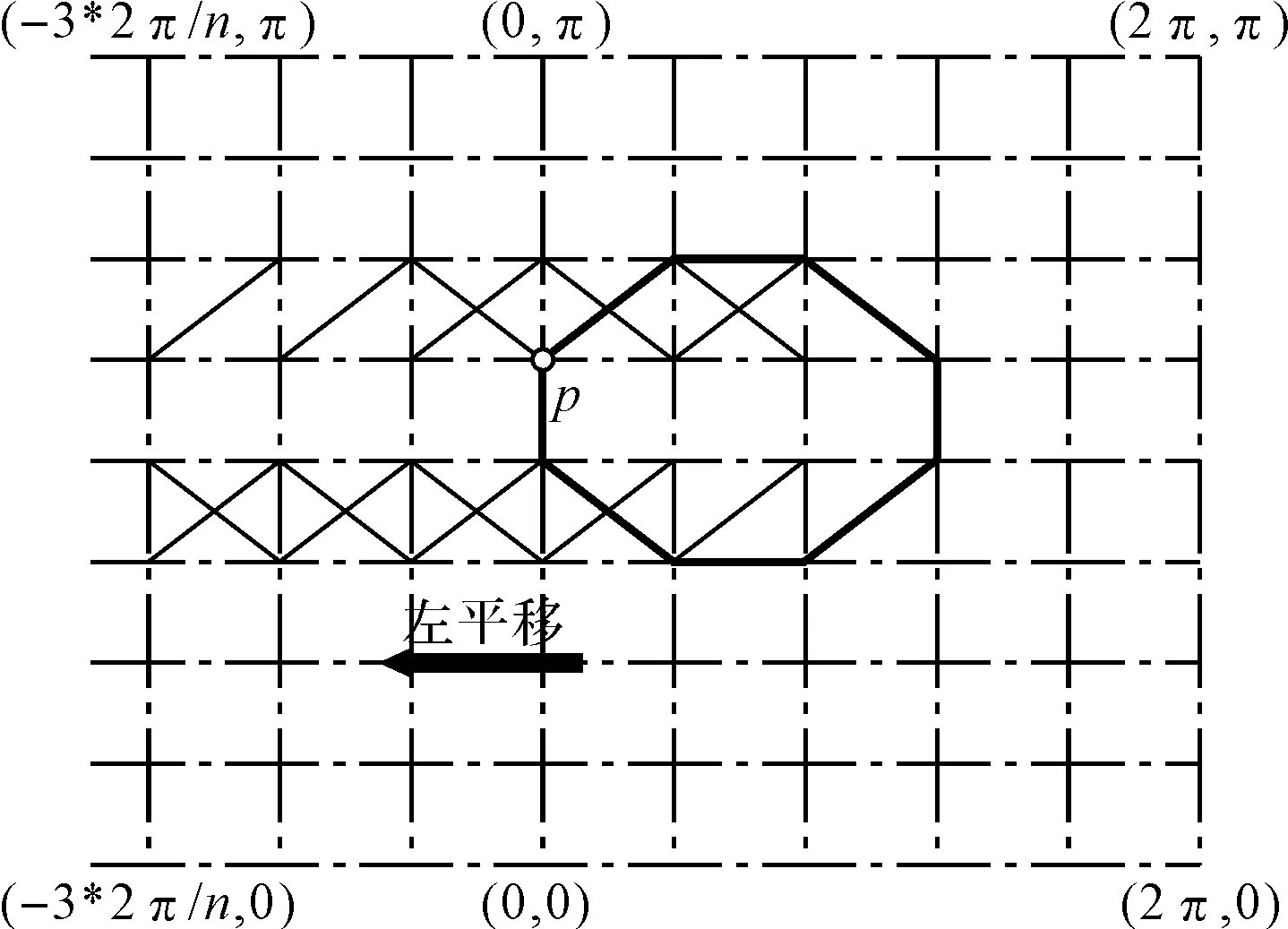
图4　B(x,y)平移图

图4所示为原始矩形域左侧边界点处B样条支集向左平移时区域添加情况,其他方向边界点处区域添加同理,此处省略。

由上述“边界宽度重合”原理得到如下添加后的区域I′×J′=[-(0+3π/n),π+3×π/n]×[-(0+3×2π/m),2π+3×2π/m](见图5)。

图5　添加后矩形域

为了进一步说明上述区域添加的正确性和必需性,下面给出在任意添加后区域I″×J″=[0,π+1×π/n]×[0,2π+1×2π/m]上拟合出的球面效果图(非封闭)作为对比,如图6(a);而在正确添加后区域I′×J′=[-(0+3π/n),π+3×π/n]×[-(0+3×2π/m),2π+3×2π/m]上拟合出的封闭球面效果图如图6(b)。

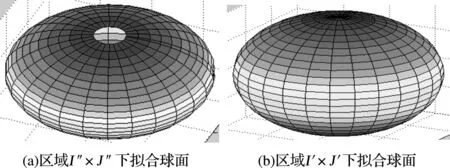
图6　添加后区域下拟合球面

从图6中对比可以看出,由于“边界宽度重合”方法中边界添加不当,导致球面拼接处无法重叠拼接以致封闭。

4.3实验结果分析

为了证明本文拟插值算法能够改善一类Box Splines空间中的封闭曲面重构的时间复杂度,下面将从算法本身深入说明,构造所得拟插值算子具体运算过程如下:

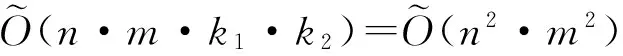
可是根据上述局部支集B(x,y)平移条件可得,本文拟插值算法运算过程实际如下:

对于任意局部支集,当其平移到局部支集原始边界意外的位置时,结果均为0,所以本文拟插值算法只对局部支集平移范围内结果不为0的区域进行计算,进而得到拟插值算法实际时间复杂的为O(n·m·k1·k2)=O(n·m·3·3)≅O(nm)。因此,本文拟插值方法对一类Box Splines空间中的封闭曲面重构的时间复杂的进行了很大改善。

表1所示,给出了不同m和n的取值情况下,拟插值算子W和W′的相应运算时间的比较。

表1　运算时间比较

5　结语

[1] P Zwart. Multivariate splines with non-degenerate parcirions[J]. SIAM J. Nurmer. Anal,1973,10(4):665-673.

[2] 王仁宏,李崇君,朱春钢.计算几何教程[M].北京:科学出版社,2008:61-71.

WANG Renhong, LI Chongjun, ZHU Chungang. Computational Geometry Tutorial[M]. Beijing: Science Press,2008:61-71.

[3] E. Ameur, D. Sbibih, C. Lger, et al. New spline quasi-interpolant for fitting 3D data on the sphere: Applications to medical imaging[J]. IEEE Signal Processing Letters,2007,14(5):333-336.

[4] G. E. Fasshauer, L. L. Schumaker. Scattered Data Fitting on the Sphere. Mathematical Methods for Curves and Surfaces Ⅱ, M. Daehlen, T. Lyche and L.L. Schumaker (eds.), Vanderbilt Univ. Press,1998:117-166.

[5] 王仁宏,崔锦泰.关于一个二元B样条基[J].中国科学,1984(9):784-795.

WANG Renhong, CUI Jintai. A Quadratic B Spline Basis Function[J]. Science in China,1984(9):784-795.

[6] E. B. Ameur, D. Sbibih. Quadratic spline wavelets with arbitrary simple knots on the sphere[J]. J. Comput. Appl. Math,2004,162(1):273-286.

[7] O. Nouisser, D. Sbibih, P. Sablonniere. A family of spline Quasi-interpolants on the sphere[J]. Numer. Algorithms,2003,33:399-413.

[8] M. Neamtu, L. L. Schumaker. On the approximation order of splines on the spherical triangulations[J]. Adv.Comput. Math.,2004,21:3-20.

[9] 祁伟丽,秦新强.基于B样条的平面轮廓重构闭合曲面算法[J].计算机技术与发展,2008,18(7):112-115.

QI Weili, QIN Xinqiang. The Algorithm of Planar Contour Restructures Closed Surface[J]. Computer Technology and Development,2008,18(7):112-115.

[10] Ahmed Boujraf, Driss Sbibih, Christophe Leger. A spline quasi-interpolant for fitting 3D data on the sphere and applications[C]//2012, EUSIPCO august: 27-31.

[11] G. Wang, Y. Li. Optimal properties of the uniform algebraic Trigonometric B-spline[J]. Comput. Aided Geomet. Des.,2006,23:226-238.

A Class of Reconstruction Method for Closed Surfaces in Box Splines Space

GUO WangLU You

(College of Geophysics and Information Engineering, China University of Petroleum, Beijing102249)

Box Spline, genus, quasi-interpolation operator, boundary width overlap, closed surfaces reconstruction

2016年3月15日,

2016年4月20日

郭旺,女,硕士研究生,研究方向:计算可视化、封闭曲面重构造。路游,男,博士,副教授,研究方向:计算几何、图形学、虚拟现实。

TP391.7DOI:10.3969/j.issn.1672-9722.2016.09.006