考虑路段拥堵的最短时间流优化问题*

黄宇达　李学威　赵红专　王迤冉

(1.周口职业技术学院信息工程系　周口　466000)(2.重庆大学自动化学院　重庆　400044) (3.周口师范学院计算机科学与技术学院　周口　466000)



考虑路段拥堵的最短时间流优化问题*

黄宇达1李学威1赵红专2王迤冉3

(1.周口职业技术学院信息工程系周口466000)(2.重庆大学自动化学院重庆400044) (3.周口师范学院计算机科学与技术学院周口466000)

针对以往对交通网络系统中路网时间流问题没有考虑网络拥塞的情况,研究了决策者如何制定最短时间流的决策问题,建立了静态数学规划模型,给出了模型的算法,讨论了算法的复杂性。随后,又对网络时间流问题进行了进一步的深入研究,分析了动态堵塞情形下的时间流特性,考虑交通网络堵塞程度对通过时间的影响,引进堵塞系数,构造动态时间函数,建立了在动态堵塞情况下的最短时间流模型,并给出了模型的算法,同时用算例验证了方法的有效性。

路段拥堵; 最短时间流; 预估时间; 堵塞系数

Class NumberTN915.01

1　引言

最短时间流问题作为一个经典问题一直存在于网络通信、交通运输以及工程规划等领域。目前,由于实际生活中的交通、信息传输等网络系统中堵塞现象日益严重,有关网络系统中流量堵塞程度问题的研究也逐渐受到关注。又由于经典网络流理论已不能解决社会和管理实践中所遇到的一些新问题,它需要向新的方向发展,这就迫切需要一套完整的有关堵塞流的理论体系。堵塞流理论便是以解决这些问题为目的而构建的。堵塞流理论是网络流规划理论中的非确定性、随机多值性研究领域中的一个新分支,它是网络流理论研究中的一个具有开拓性和创新性的前沿领域[1～2]。以往对交通网络系统中路网容量和时间流问题的研究中,大都是从网络最大流的角度出发进行研究的。

在现实交通系统中,当交通网络系统具备由于不同主体出行行为的选择不同造成交通流动的随机性或交通网络结构的不合理等堵塞条件时,堵塞现象就可能会发生。这时在网络中就产生了堵塞流动,造成交通网络系统的堵塞。譬如在交通拥挤和紧急疏散网络中,拥挤的车辆和慌乱的人群不会按照指定的规则运动,在网络中常发生堵塞,交通个体无法继续向前移动,而各流动单元又不愿意向回撤退,产生堵塞流动,此时网络中的流量已达到饱和,不能再增加[3～5]。堵塞流动也是交通网络系统中常见的一类流动,然而以往对路网容量和时间流问题的研究主要没有考虑交通网络系统堵塞的情况。

因此,本文从网络系统堵塞的角度研究了最短时间流问题。在研究路段拥堵的最短时间流模型的基础上,设计了考虑路段拥堵的最短时间流的预估时间增量比较算法,最后通过算例分析进一步验证了算法的有效性。

2　考虑路段拥堵的最短时间流模型

为了模型研究方便,给出以下定义[7]:

定义1:基本路径Pk是指路网N中任意一条由υs到υe的通路,通路上的每条弧方向与流向一致。

定义2:沿任意通路上的单位流动称为单位基本流。

定义3:某可行流f是无环流,若它至少可以用一种由单位基本流的线性关系表示,即f=α1ξ1+α2ξ2+…+αmξm,ξi(i=1,2,…,m)有m条单位基本流,αi(i=1,2,…,m)是非负数。

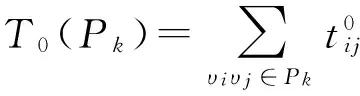
若可行流f由m条基本流构成,则可行流f通过网络的时间为其中最长的基本流的时间。

定义5:可行流f的时间为

(1)

其中,f+为f正向路。

在经典的网络流理论中,一般只考虑流通能力问题,与时间无关。而在以时间为优化目标的网络流规划中,路段内形成的拥堵则直接影响交通流的速度,因此不能忽略形成的拥堵对通过时间的影响。

当流动主题的流量从0开始时,交通流主体通行率高,流动快;随着流量的加大,流速开始受到逐渐形成的拥堵的影响而变慢。所以,通过每一段路的时间是通过该路段流量的函数。可以用近似描述函数表示:

(2)

结合以上定义,路段拥堵最短时间流问题可以表达成:

(3)

3　考虑路段拥堵的最短时间流的预估时间增量比较算法

若把时间作为各弧段的一个权值,那么容易联想到类似算法就是经典网络流理论中的最小费用流算法。基本思路是:从零流量开始f(0),首先对当前流f(0)构造所有可能增加流量的增广链,然后在这些可能的增广链中采用最短路径算法求出最小费用增广链。在此链上增加流量,获得流量为f(1)的最小费用流。同样,对f(1)再构造所有可能增加流量的增广链,并在其中费用最小的增广链继续增加流量,获得流量为f(2)的最小费用流[10]。如此反复类推,直到网络中不存在增广链。在此思路中将费用推广到时间,得到的就是最短时间流。但计算方法有一些改变。

3.1构造基于最小费用流算法的增量网络

定义6:增量网络是指对于给定的带起点υs和终点υe的路网N=(V,A,C,T)以及N上的可行流f,假定A+(f)={(υi,υj)|(υi,υj)∈A,fij0}。因为N中任何一对顶点之间最多有一条弧,从而可以得到A+(f)∩A-(f)=∅,令A(f)=A+(f)∪A-(f),且∀(υi,υj)∈A(f),于是:

(4)

从而得到网络N的关于流f的增量网络N(f)=(V,A(f),C(f),T(f))。

基于求解最小费用流的赋权图算法,得到最短时间流算法的基本思想为:从零流量开始f(0),在从起点到终点的所有可能增加流量的增广路径中寻求总时间最短的路径,并在此路径上增加流量,获得流量为f(1)的最短时间流。再对f(1)寻求所有可能增加流量的增广路径,并在其中总时间最短的增广路径上继续增加流量,得到流量为f(2)的最短时间流。不断重复以上过程,直到网路中不再存在增广路径,无法增加流量,搜索结束。上述过程的每一步都是对当前最短时间流寻找最短时间的增广路径并进行增流,按照定义5,新的增广路时间为增流后总流量通过该网络的最短时间[11]。而对某一最短时间流不存在最短时间增广路时,此过程得到的最大流即为最短时间最大流。

在构造基于最小费用流算法的增量网络的基础上,寻求增量网络中时间最短的增广路,在此之前需先计算各条增广路的时间。

3.2增广网络中增广路时间的确定方法

增广网络中增广路时间的确定主要存在以下三种情况:

1) 原网络中不存在含有反向弧的增广链时,该增广路的时间是构成该增广路的各弧段的时间之和,即

(5)

2) 当网路中含有反向弧增广链时,该增广路的时间为该增广路径增加一个单位流量后形成的新流量分布中,时间最长的单位流时间。

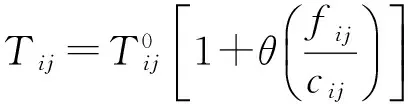
在实施预估时间增量比较法时,每次流量的增加应以一个单位的流量的进度迭代进行[14]。根据以上分析,得到考虑路段时间的最短时间流算法如下:

Step1:设定初始流量f(0)=0;

Step2:构造当前流f(0)的增广网络N;

Step5:如此循环,直到得到最短时间流,算法结束。

4　算例分析

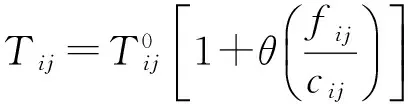
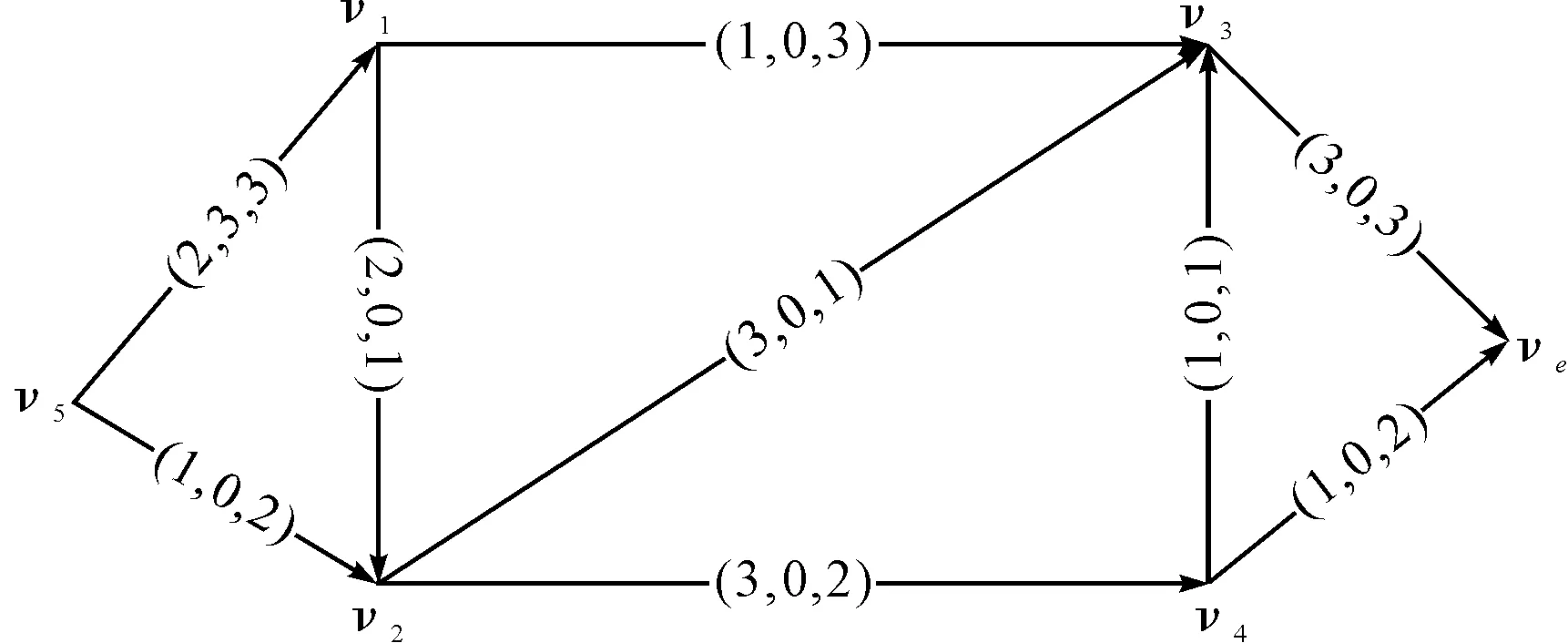
图1　构造的初始零流状态路网图

依据考虑路段时间的最短时间流算法,迭代过程如表1所示。

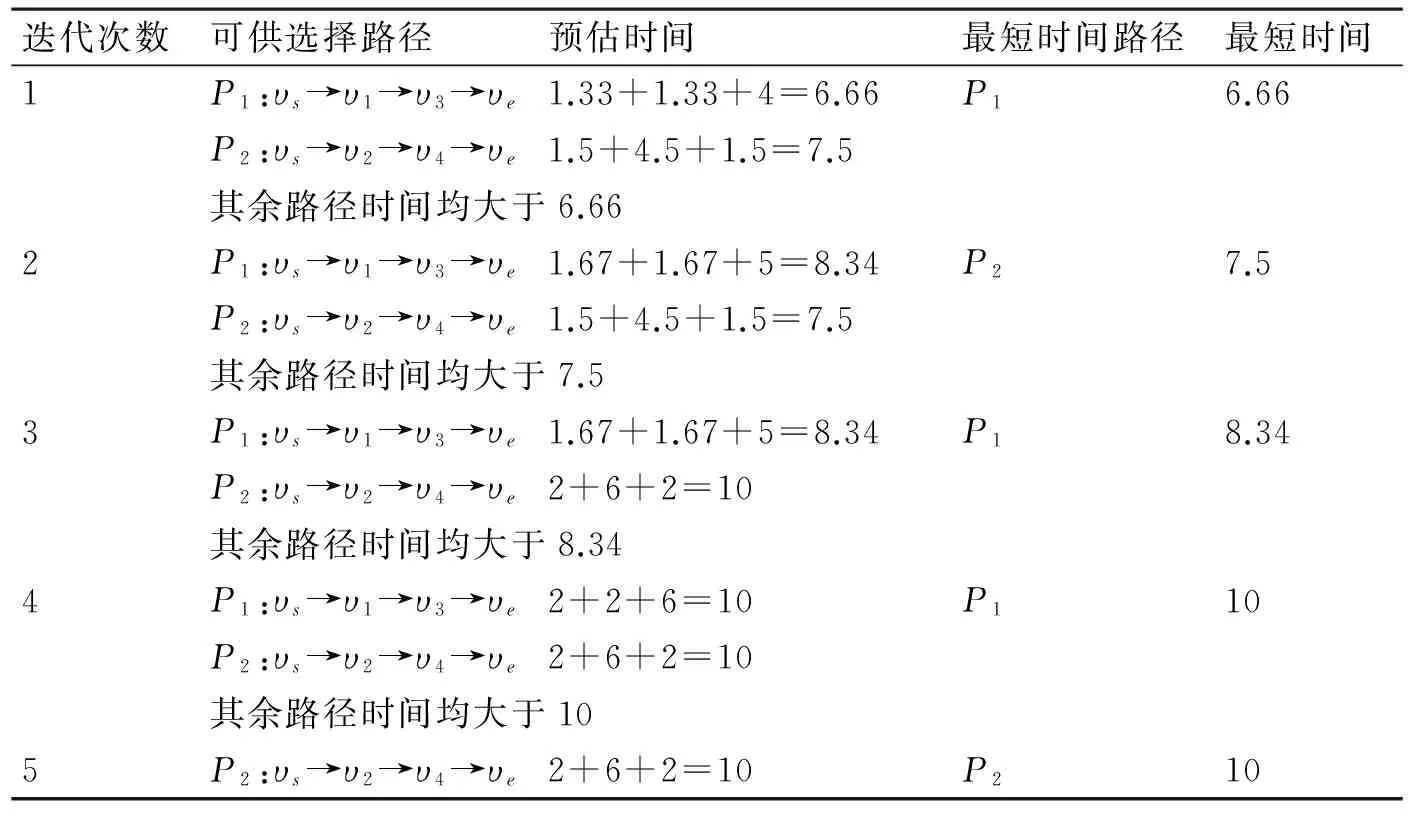
表1　迭代过程

最终优化结果如图2所示。

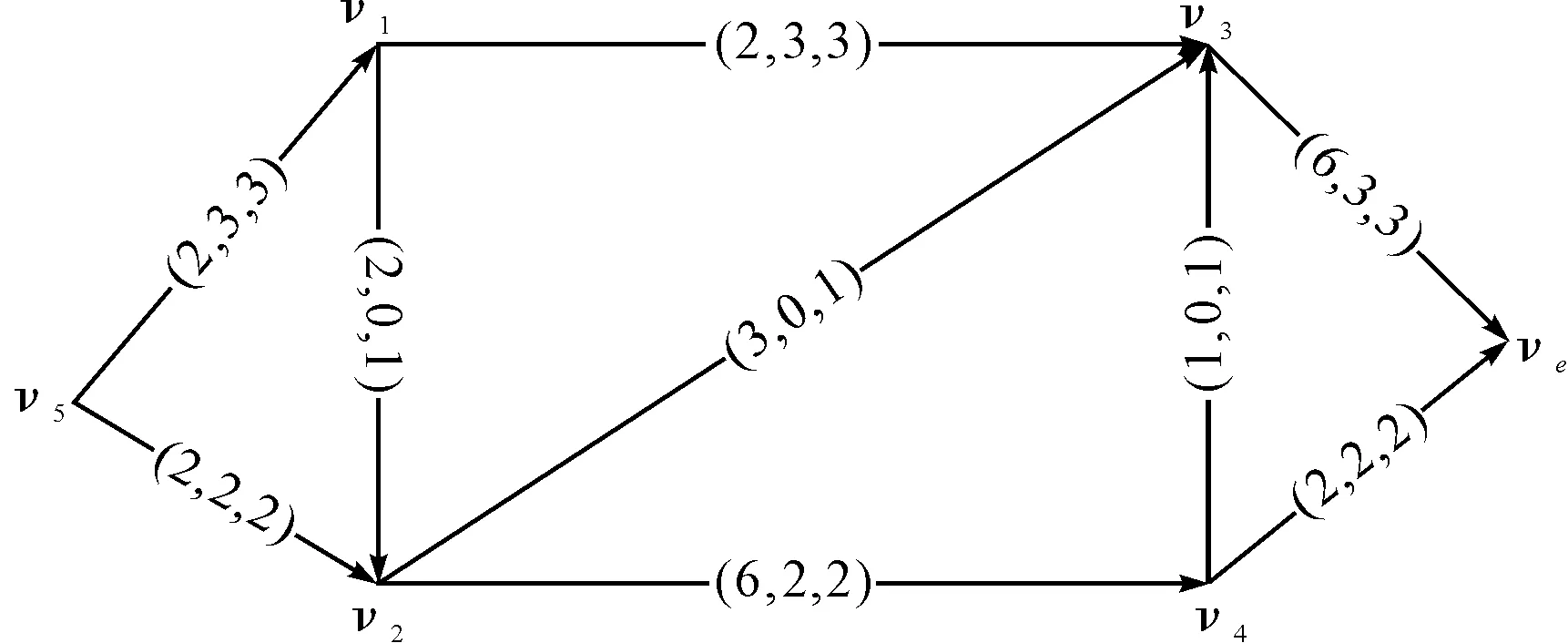
图2　动态阻塞优化结果

经过考虑路段时间的最短时间流算法得到满足最短时间的最大流分布图,即在算例中流量为5个单位时,在考虑动态阻塞的情况下的最短时间为T=2+2+6=10,保证给定的流量顺利流出。

若不考虑动态阻塞情形,则上述算例的优化最短时间最大流如图3所示。

图3　静态阻塞优化结果

考虑动态阻塞和考虑静态情形的优化最短时间流曲线对比如图4所示。

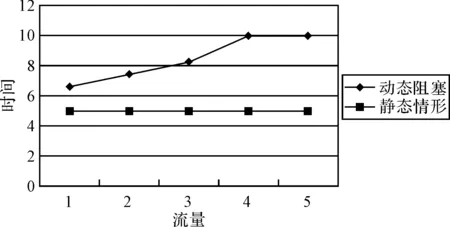
图4　流量-最短时间图

由上述案例分析可知,当流量变化时,由于考虑了动态阻塞情况,造成时间延迟,当流量越来越大时。阻塞越来越严重,故通行的时间会增加;当不考虑阻塞程度对路段时间的影响时,通行时间会小于网络发生动态阻塞时的时间。

5　结语

本文在目前交通系统的大背景下,考虑到如今日益严重的交通拥塞问题,对决策者在最短时间流如何制定的问题方面进行了进一步研究,在给出所建立的数学模型对应算法的同时,又对算法的复杂性进行了分析和探导,最后通过算例分析进一步验证了该算法的有效性和合理性,从而为交通拥堵特殊情况下的交通合理规划提供建设性参考。

[1] 宁宣熙.堵塞流理论及其应用[M].北京:科学出版社,2005:1-100,162-176.

NING Xuanxi. Blocking flow theory and its application[M]. Beijing: Science Press,2005:1-100,162-176.

[2] 陈春妹,任福田,荣建.路网研究综述[J].公路交通科技,2002,19(3):97-101.

CHEN Chunmei, REN Futian, RONG Jian. Review of research on road network[J]. Highway Traffic Science and Technology,2002,19(3):97-101.

[3] Hai Yang, Michael G. H. Bell, Qiang Meng. Modeling, The Capacity and Level of service ofUrban Transportation Networks[J]. Transportation Research PartB,2000(34):255-275.

[4] 周溪召.大城市中心区道路交通供求模型及其应用[D].上海:同济大学,1995.

ZHOU Xizhao. The road center of big city traffic supply and demand model and its application[D]. Shanghai: Tongji University,1995.

[5] S. C. WONG, HAI YANG. On the Reserve Capacity of Priority Junctions and Roundabouts[J]. Transpn. Res.-B,1996,30(6):441-453.

[6] S. C. WONG, HAI YANG. Reserve Capacity of a Signal-controlled Road Network[J] . Transpn. Res.-B,1997,31(5):397-402.

[7] 杨涛.运输网络极大流动态诊断模型[J].中国公路学报,1991,4(1):72-77.

YANG Tao. A dynamic diagnosis method of the maximum flow in transportation network[J]. Journal of Highway Chinese,1991,4(1):72-77.

[8] 杨涛.城市交通网络总体性能评价与建模[D].南京:东南大学,1995.

YANG Tao. The overall performance evaluation and modeling of city traffic network[D]. Nanjing: Southeast University,1995.

[9] 谈晓洁,周晶,盛昭翰.城市交通拥挤特征及疏导决策分析[J].管理工程学报,2003,17(1):56-59.

TAN Xiaojie, ZHOU Jing, SHENG Zhaohan. The crowded city traffic grooming feature and decision analysis[J]. Journal of Engineering Management,2003,17(1):56-59.

[10] 宁宣熙.有向网络的最小流问题及其分支定界解法[J].系统工程,1996,14(5):61-66.

NING Xuanxi. A branch and bound method to its minimum flow problem of directed network[J]. Systems Engineering,1996,14(5):61-66.

[11] 宁宣熙.求解网络最小流的双向增流算法[J],系统工程,1997,15(1):50-57.

NING Xuanxi. The minimum flow for solving the network two-way flow increasing algorithm[J]. Systems Engineering,1997,15(1):50-57.

[12] 黄孝鹏.堵塞流理论在路网容量和最短时间流中的应用研究[D].南京:南京航空航天大学,2007.

HUANG Xiaopeng. Study on application of flow theory in network capacity and the minimum time flow blocking[D]. Nanjing: Nanjing University of Aeronautics & Astronautics,2007.

[13] Ning Xuanxi. The minimum flow problem of a transportation network and its approximate Solution[C]//Proceedings of ISIM’96, Nanjing: 488-492.

[14] 孙宇.运输网络中的最小堵塞流问题及其算法研究[D].南京:南京航空航天大学,1997.

SUN Yu. Study on the minimum blocking flow problem and its algorithm in the transportation network[D]. Nanjing: Nanjing University of Aeronautics & Astronautics,1997.

Shortest Time Flow Optimization Problem Considering Congestion

HUANG Yuda1LI Xuewei1ZHAO Hongzhuan2WANG Yiran3

(1. Information and Engineering Department, Zhoukou Vocational and Technical College, Zhoukou466000) (2. College of Automation, Chongqing University, Chongqing400044) (3. College of Computer Science and Technology, Zhoukou Normal University, Zhoukou466000)

Aiming at the time flow problem of traffic network system without considering the case of network congestion in the past, how the policy makers make the minimum time flow decision problem is studied and a static mathematical programming model is proposed, then the model algorithm is given, the complexity of the algorithm is discussed. Next, the network time flow problem has been further studied, the dynamic plugging circumstances of the time stream is analyzed, the traffic network congestion degree of influence through time is considered and the congestion coefficient is introduced, then a dynamic time function is presented, the shortest time congestion flow model in dynamic condition is established and the algorithm is given based on the model. Finally, the validity of the method by an example is verified.

road section congestion, minimum time flow, estimate time, block coefficient

2016年3月10日,

2016年4月22日

重庆市科技攻关计划项目(编号:CSTC2012gg-yyjsB30001);河南省基础与前沿技术研究计划项目(编号:122300410397)资助。

黄宇达,男,硕士,副教授,研究方向:知识工程,信息安全与控制,计算机网络等。李学威,男,硕士,讲师,研究方向:智能控制,计算机网络。赵红专,男,博士研究生,研究方向:嵌入式系统,自动化控制等。王迤冉,男,硕士,副教授,研究方向:计算机网络,人工智能等。

TN915.01DOI:10.3969/j.issn.1672-9722.2016.09.003