基于Plant Simulation的机车驱动装置组装线仿真及优化研究

王　强

(中国铁路总公司运输局　机务部， 北京 100844)



专题研究

基于Plant Simulation的机车驱动装置组装线仿真及优化研究

王强

(中国铁路总公司运输局机务部， 北京 100844)

机车的驱动装置的组装是机车制造和大修生产的关键工序，通常是制约产量的瓶颈环节。在既有厂房空间限制之下，利用离散事件系统仿真方法，借助于Plant Simulation软件工具，对组装线进行数据分析、系统建模和优化，找到符合绩效期望的工装台位设置改进措施，可以为企业开展工艺布局的改进调整提供有效的决策依据。本文基于一个实例对上述过程进行了完整的介绍。

Plant Simulation； 机车； 驱动装置； 离散事件； 系统仿真

在计算机技术发展的支持下，系统仿真技术得到了快速发展，已广泛应用于各种工程和非工程领域。特别是在制造业的产品设计、试验、制造、维护等方面发挥了提高效率、节约成本、提升质量等重要作用。其中，针对工厂车间生产系统的设计和优化，国内外已发展出很多较为成熟的仿真系统，Plant Simulation是Tecnomatix开发的面向对象的集成化层次化系统建模和仿真软件平台，适用于对生产设施、工艺布局、物流配送等过程的仿真分析和优化。

图1　机车驱动装置(半悬挂)主要部件构成

随着十几年的技术创新和升级，我国铁路机车制造及大修技术已经取得了长足的进步，装备水平和工艺能力都能够满足高性能产品的生产制造，但对于轮轴驱动装置等一些较复杂的关键系统的组装等生产环节中，面对计划安排的不均衡性和返修需求的不确定性时，也暴露出生产线产能的不足。在既有生产厂房空间和主要设施条件下，借助于现代系统仿真技术来找到工艺布局和工装台位优化方案，达到既满足产能需求，又控制成本投入的目标，是一种有效的解决途径和应对需求变化的能力储备。

以某机车制造企业驱动装置组装线为例，针对产能提升的需求目标，利用离散系统仿真方法，基于Plant Simulation软件工具，研究提出工艺优化的建议方案。

1　项目描述及绩效目标

机车驱动装置(见图1)是机车的重要部件，其组装是机车制造过程中的关键工序，往往是机车制造的瓶颈环节，其生产能力决定了整车的生产和大修能力。

某公司驱动装置组装生产在一个单独的车间内全部完成。既有系统的实际生产能力为新造加返修约23台/月，产量记录(某半年)见表1。为了满足集中订单的交货期要求，经分析必须提高到新造35台/月，同时满足不定期的返修生产要求。机车的驱动装置主要由车轴、大齿轮、小齿轮、齿轮箱、报轴箱、牵引电机等部件组成。其组装的工艺流程见图2，主要工序和台位设置见表2。

表1　某年上半年驱动装置生产完成记录

2　现场数据收集整理

2.1主要工序的平均加工时间

根据工厂的工时定额分析数据，得到各工序平均加工时间见表3。

图2　某公司机车驱动装置组装工艺流程图

序号工装名称数量用途1清洗机1除车轴外所有零件清洗2大齿轮压装机1大齿轮与车轴安装3抱轴箱组装台12抱轴箱装配,轴承内圈,密封圈采用热装,在此工作台冷却3h后进行测量轴承间隙,所以需要较多的工作台保持均衡生产。4小齿轮压装台1用于小齿轮压装在电机轴上5电机安装台1用于电机与抱轴箱(含车轴、大齿轮)安装。6齿轮箱装配台架12用于齿轮箱的安装和安装后的临时存放。7返修台1用于返修驱动装置的定置修理。8例行试验台3用于驱动装置例行试验,主要检测轴承温度、振动、扭矩参数。9待喷漆台20用于试验完成的驱动装置存放,待喷漆。10喷漆房2在组装后实行整体油漆,烘干。11吊车3分配如下:大齿轮压装和抱轴箱组装1台,电机安装与齿轮箱安装1台,油漆和发运1台。

表3　工序平均加工时间(具体内容略)

2.2喷漆工序的实际加工时间采集

对于现场观察认为的瓶颈工序——喷漆的实际加工时间的历史记录进行的采集，筛选整理了50组数据见表4。

2.3返修到达记录

为了分析返修到达的情况，查询车间的台账并得到了一组返修到达的记录整理数据见表5。

3　输入数据分析

3.1部件到达

根据工厂的实际情况，因驱动装置组装是整个生产的瓶颈环节，所以工厂的生产管理保障了所需的部件无延迟供应，车轴、大齿轮、抱轴箱、电机、小齿轮、齿轮箱等部件的到达可以认为是时间间隔为常数的连续到达。

3.2返修到达

根据表5的数据记录进行如下分析：

(1)评估数据的独立性：进行相关性检验，绘制到达间隔的散点图如图3，同时计算其相关性系数为0.018，据此可判断数据无强相关性。

表4　喷漆时间记录　h

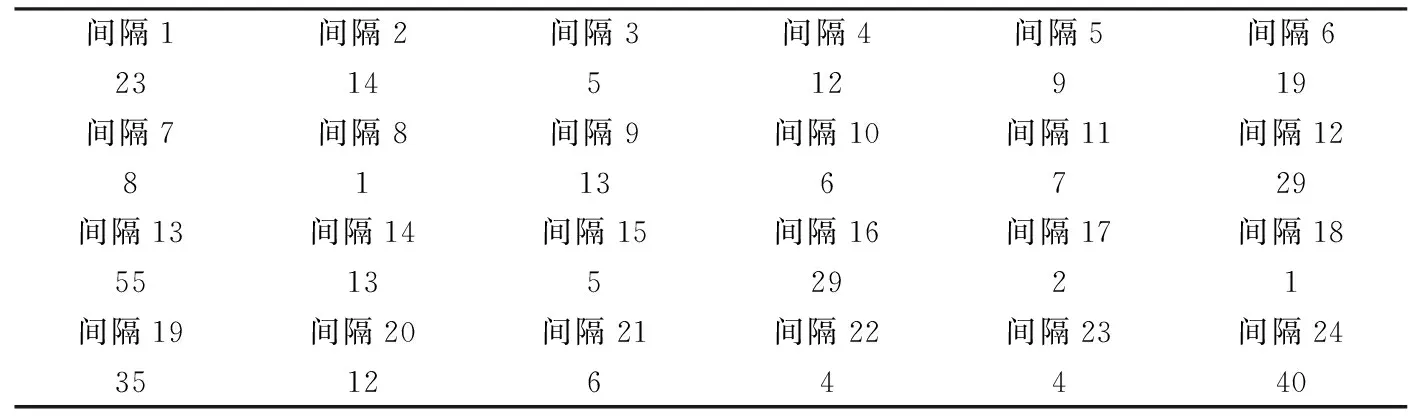
表5　返修到达时间间隔　h

图3　驱动装置返修到达时间间隔记录的散点图

(2)点统计：返修到达时间间隔记录的点统计数据如表6。从数据看，变异系数cv=0.947接近于1，偏度1.29>0为右偏，倾向于指数分布。

表6　返修到达间隔时间的点统计

3.3喷漆加工时间

根据表4的记录进行如下分析：

(1)评估数据的独立性：进行相关性检验，绘制加工时间的散点图如图4，同时计算其相关性系数为0.011，据此可判断数据无强相关性。

(2)点统计：喷漆加工时间记录的点统计数据如表7。从数据看，变异系数cv=0.06接近于0，偏度-0.267接近于0，倾向于对称分布。

图4　喷漆加工时间记录的散点图

参数数值样本数50最小值2.99最大值3.95平均值3.5206标准差0.193817方差0.037565偏度-0.26628变异系数0.055052

图5　喷漆加工时间记录的正态检验

4　系统仿真模型的建立

4.1系统模型

根据系统的实际情况和输入数据的分析，应用Plant Simulation 9 软件建立系统的模型，首先建立现场模型，2D模型如图6所示。

图6　Plant Simulation 9现场模型(2D)

4.2模型的参数和控制说明

(1)部件到达

车轴、大齿轮、抱轴箱、电机、小齿轮、齿轮箱等均以时间间隔为常数(1 h)的连续到达。

(2)返修到达

以β=15的负指数分布到达。

(3)加工时间

各主要台位(除喷漆外)处理时间设为常数(见表3)，喷漆工序处理时间按照μ=3.5,σ=0.19的正态分布。

(4)吊车控制

根据实际生产情况，主要部件的车间内搬运由3台吊车完成，3台吊车的任务分配见表8。吊车的控制在模型中通过SimTalk编程实现。

5　仿真试验(既有现场模型)及其输出分析

5.1仿真试验设置

非终止型仿真；仿真时间按照仿真运行时间为6个月、每天为一班制(8 h)、总1 440 h设定；另设置预热期为120 h；重复运行5次。

表8　吊车任务分配

表9　仿真运行试验(现场模型)——生产指标数据

5.2输出分析

(1)输出数据汇总整理见表9和表10。

(2)仿真模型的校验：从仿真运行试验输出的生产指标数据分析，其月产量与表1的实际统计数据(按照6个/台计算)基本相符，可认为仿真模型符合现场实际情况。

(3)瓶颈分析：从仿真运行试验输出的工序过程数据分析，此时限制产量的瓶颈工序为喷漆台，2个喷漆台的平均利用率达到99.01%，而20个待喷漆台的堵塞率达到99.67%。

(4)改进方案1：增加1个喷漆台。

6　仿真试验(改进方案1模型)及其输出分析

6.1模型更新及仿真试验设置

在模型中增加1个喷漆台并修改相应程序代码(见图7)，仿真试验设置不变。

表10　仿真运行试验(现场模型)——工序过程数据　%

图7　Plant Simulation 9改进方案1模型

6.2输出分析

(1)输出数据汇总整理见表11和表12。

(2)绩效改进评估：从仿真运行试验输出的生产指标数据分析，其中月产量改进到30.7台，但仍低于期望产量35台，需进一步改进。

(3)瓶颈分析：从仿真运行试验输出的工序过程数据分析，此时3个喷漆台的平均利用率仍达到98.43%，仍为瓶颈工序。20个待喷漆台的堵塞率降低到85.62%。同时，3个试验台的平均利用率上升到90.84%，将成为另一个瓶颈环节。

(4)改进方案2：再增加1个喷漆台和1个试验台。

7　仿真试验(改进方案2模型)及其输出分析

7.1模型更新及仿真试验设置

在方案1模型中增加1个喷漆台和1个试验台并修改相应程序代码(见图8)，仿真试验设置不变。

7.2输出分析

(1)输出数据汇总整理见表13和表14。

表11　仿真运行试验(方案1)——生产指标数据

表12　仿真运行试验(方案1)--工序过程部分数据　%

图8　Plant Simulation 9改进方案2模型

月产量试验1试验2试验3试验4试验5平均月产量(新造)216216213216216215月产量(返修)171715181917返修完成百分比100.099.04100.099.06100.099.62

表14　仿真运行试验(方案2)——工序过程部分数据　%

(2)绩效改进评估：从仿真运行试验输出的生产指标数据分析，其中月产量改进到35.8台，大于期望产量35台，且返修的完成比例达到99.62%，所以该改进方案可以满足新的生产能力要求。

(3)方案优化分析：按照方案2可以实现预期的目标，方法是增加1个试验台和2个喷漆房，在现有车间工艺布局下将受到空间的限制。进一步分析仿真运行试验输出的工序过程数据，此时12个抱轴箱组装台的平均利用率仅达到37.46%，12个齿轮箱组装台的平均利用率仅达到6.74%，所以存在减少上述几种台位以便腾出空间用于增加试验台和喷漆台的可能。

(4)改进方案3：减少抱轴箱组装台、齿轮箱组装台的数量。以抱轴箱组装台为例进行数量的计算如下：

从方案2的仿真运行数据中得到12个抱轴箱组装台的部件总到达数量为1 296个，则可计算其平均到达速率为

λ=1 296/1 440=0.9(件/h)

抱轴箱组装台的加工时间为常数5 h，即加工速率为：

则理论上所需的抱轴箱组装台数量为：

考虑到生产线应留有裕度和生产启动过程中的需要，确定改进方案3为将抱轴箱组装台和齿轮箱组装台各减少到6个。

8　仿真试验(改进方案3模型)及其输出分析

8.1模型更新及仿真试验设置

在方案2模型中减少6个抱轴箱组装台和6个齿轮箱组装台并修改相应程序代码(见图9)，仿真试验设置不变。

8.2输出分析

(1)输出数据汇总整理见表15和表16。

图9　Plant Simulation 9改进方案3模型

月产量试验1试验2试验3试验4试验5平均月产量(新造)211216210210210211月产量(返修)161618191416返修完成百分比100.0100.0100.0100.0100.0100.0

表16　仿真运行试验(方案3)——工序过程部分数据　%

(2)绩效改进评估：从仿真运行试验输出的生产指标数据分析，在保证月产量的改进(35.2台)与方案2基本相当并大于期望产量35台的情况下，可节省大量空间用于生产布局的优化调整。

9　机车驱动装置组装生产线系统仿真结论

采用改进方案3既能够满足生产绩效要求，又具有工程可实施性，为推荐方案。当然，基于上述过程，结合现场需要还可以提出和模拟其他方案。

10　结束语

通过机车驱动装置组装线工艺布局优化的实例，发挥系统仿真方法和Plant Simulation平台的强大功能优势，本文研究内容充分显现出过程清晰、结果明确的特点，为机车制造和大修生产系统的设计和优化提供了有益的参考手段。

[1]熊光楞，王昕.仿真技术在制造业中的应用与发展[J]. 系统仿真学报,1999,11(3):145-151.

[2]肖田元，张燕云，陈加栋.系统仿真导论[M].北京：清华大学出版社,2000.

[3]张如杰，杨自建,王伟，等. eM-Plant在机车预组装生产线建模与物流仿真中的应用[J]. 装备制造技术， 2012，(5)：140-143.

[4]张超，李慧，田恺. 基于Plant Simulation的航空综合在机加厂房布局仿真研究[J]. 工程设计学报， 2013，20(3)：199-207.

Research on Simulation and Optimization of Locomotive Driving Unit Assembly Line Based on Plant Simulation

WANGQiang

(Locomotive Department ,Transportation Bureau of China Railway, Beijing 100844, China)

Assembly of locomotive driving unit is the critical process of locomotive manufacturing and overhaul, it is the bottleneck link for production volume. Limited by existing workshop space, the expected improvement could be developed based on discrete system simulation method through data analysis, system modeling and optimization，assisted by Plant Simulation software tool. As a decision-making basis, the output of the simulation will be effective for process layout improvement of facilities. This paper will entirely introduce above procedure through a practice example.

plant simulation; locomotive; driving unit; discrete event; system simulation

1008-7842 (2016) 03-0016-08

男，高级工程师(

2016-03-24)

U260.2

Adoi:10.3969/j.issn.1008-7842.2016.03.04